RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 20, ES6007, doi:10.2205/2020ES000745, 2020
Yu. A. Titchenko
Institute of Applied Physics of the Russian Academy of Sciences (IAP RAS), Nizhny Novgorod, Russia
The advantage of bistatic remote sensing is the ability to measure in a remote area from the receiver and transmitter. In this case, the scattering will remain quasi-specular and is calculated in the Kirchhoff approximation. This makes it possible to obtain an explicit relationship between the scattering characteristics and the parameters of the water surface, which opens possibilities for creating new algorithms for solving the inverse problem of retrieving wave parameters. In addition, the power of the received signal in the quasi-specular reflection region significantly exceeds the power of the reflected signal in the resonant scattering region, which makes it possible to use the signals of satellite navigation systems reflected from the underlying surface for remote sensing tasks. In this work, a formula is given for the Doppler spectrum (DS) of radiation reflected by a water surface in a bistatic formulation of the problem, taking into account the antenna patterns of the receiving and transmitting antennas, taking into account the movement of the receiver and transmitter. A feature of the approach used is the description of the water surface by six second-order statistical moments. The features of the DS model are investigated depending on the geometry of the problem, on the speeds of the transmitter, and on the direction of the wave propagation. An algorithm is proposed for determining the direction of wave propagation from measurements of the DS characteristics of reflected radiation.
At present, one of the most developing areas of remote sensing of the World Ocean is research devoted to the analysis of reflected signals from satellite navigation systems. They are based on the principles of multi-position radar. The idea of analyzing signals from global navigation satellite systems (GNSS) reflected by the water surface to measure tide heights was proposed as early as 1993 [Martin-Neira, 1993]. The technique for analyzing the reflected GNSS signals is called GNSS-R. The proposal to use GNSS-R to solve a wide range of remote sensing problems seemed promising and the theoretical aspects of this approach to remote sensing began to develop rapidly [Zavorotny et al., 2014; Cardellach et al., 2011]. Today, using GNSS-R, the parameters of the sea surface, soil, vegetation, ice, and snow cover is retrieved.
Small satellites of the UK-DMC disaster monitoring mission have successfully conducted a number of experiments since 2004 to demonstrate the capabilities of analyzing reflected GPS signals from water, land, and ice cover [Clarizia et al., 2009; Gleason, 2006]. Unique experiments on the reception of GLONASS signals reflected by the water surface, considering their features and advantages, were carried out at the offshore testing area in Sweden [Hobiger et al., 2014].
A significant step forward in this area was the launch in 2016 by the American space agency (NASA) of the CYGNSS mission [Ruf et al., 2016], consisting of 8 moving one after another small spacecraft equipped with GPS signal receivers, designed to study the parameters of surface waves in tropical cyclones. Since 2017, the system is fully operational, and the measurement results are publicly available. In 2019, a group of two Chinese BuFeng-1 A / B satellites was launched into orbit, designed to restore the surface wind speed based on the analysis of reflected signals from navigation satellite systems [Jing et al., 2019].
In Russia, a system was developed for constructing radar images of the underlying surface based on the GNSS reception on unmanned aerial vehicles [Fateev et al., 2012]. An energy calculation was carried out for the possibility of placing a receiver of reflected GPS / GLONASS signals on small spacecraft to monitor the state of the sea surface [Sakhno et al., 2009].
This work is devoted to the development of an original approach for calculating the characteristics of the Doppler spectrum (DS) of quasi-specularly reflected radiation, which takes into account the antenna patterns (AP) and allows one to obtain analytical formulas explicitly expressing the relationship between the DS and the wave parameters. Initially, this approach was developed for monostatic sensing at low incidence angles [Karaev et al., 2008, 2019; Kanevskii and Karaev, 1996].
In [Titchenko and Karaev, 2016], an approach to calculating the characteristics of DS radiation reflected by a water surface in a bistatic formulation of the problem for a stationary receiver and transmitter began to form. In [Titchenko et al., 2017], a particular case of radiation and reception along one straight line parallel to the direction of wave propagation was considered and the first algorithm for retrieving six wave parameters was proposed in the presence of three antennas with different AP at the receiving point. The next step was to consider the movements of the receiver and transmitter in the formulas [Titchenko and Karaev, 2018]. The work [Titchenko and Karaev, 2019] is devoted to the study of the influence of wave parameters on the characteristics of the reflected radiation when taking into account the AP and it is theoretically shown that for the optimal solution of the inverse problem it is possible to use the width and shift of the DS of the reflected radiation in addition to the traditional backscattering cross-section with the correct choice of AP.
In this work, the formula for the DS of reflected radiation is presented for the first time in the bistatic formulation of the problem, considering the AP of the receiving and emitting antennas.
 |
| Figure 1 |
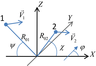
Experimental measurements have shown that four characteristic regions can be distinguished in the scattering of waves by the sea surface [Bass and Fuks, 1979; Valenzuela, 1978]. At angles of reflection close to specular, the scattering has a quasi-specular character and is well described by the tangent plane approximation (Kirchhoff's approximation). Resonant scattering, described by the perturbation method, dominates in the region of average angles of deviation from the specular beam. In the transition region of receiving angles to describe scattering, it is necessary to use both methods simultaneously. If sensing occurs at small grazing angles, then shading must be considered. Let us consider the scattering of waves by the sea surface in the quasi-specular reflection region. Figure 1 shows the problem statement.
In the figure, the number 1 marks a transmitter emitting a wave with a wavenumber $k=2\pi/\lambda$, $\lambda$ – wavelength. The number 2 marks the receiver. Points 1 and 2 are moving at speeds $\vec V_1(V_x,V_y,V_z)$ and $V_2(Vr_x,Vr_y,Vr_z)$. The direction of wave propagation $\varphi$ is measured from the positive direction of the $X$ axis. AP are assumed to be Gaussian and $\delta^2_{xr}$, $\delta^2_{yr}$, $\delta^2_{xt}$, $\delta^2_{yt}$ – width of the AP of the receiving and transmitting antennas at half power level in the $X$ and $Y$ planes. Grazing angle for the transmitter – $\psi$. Grazing angle for the receiver – $\chi$. Distance from the transmitter to the center of the AP footprint on the water surface – $R_{01}$. Distance from the receiver to the center of the AP footprint on the water surface – $R_{02}$. In comparison with the geometry considered in [Titchenko and Karaev, 2018], in this case, it was assumed that the receiver, transmitter, and the point of intersection of the AP footprint centers with the water surface are located in the same plane $Y=0$. In this case, to simulate the case of backscattering, the grazing angle of the receiver should be calculated as follows: $\chi=180\mbox{°} - \psi$.
In the Kirchhoff approximation for the Fraunhofer zone, assuming a normal distribution of surface heights and the absence of shading, the DS shape will be described by the following Gaussian formula:
\begin{eqnarray*} S_0 (\omega) = \end{eqnarray*} \begin{eqnarray*} \frac{|V^2_{eff}|\exp\Bigg(\displaystyle{-\frac{\left(C_{Ry}+\sigma^2_{yy}\right)\tan^2{\frac{\psi-\chi}{2}}} {2(\left(C_{Ry}+\sigma^2_{yy}\right)\left(\sigma^2_{xx}+C_{Rx})-K^2_{xy}\right)}}\Bigg)} {2k\cos^4\frac{\psi-\chi}{2}\sqrt{\left(C_{Ry}+\sigma^2_{yy}\right)\big(\sigma^2_{xx}+C_{Rx}\big)-K^2_{xy}}} \times \end{eqnarray*} \begin{equation} \tag*{(1)} \frac{\sqrt\pi}{\sqrt{\omega_s}}\exp\Big(-\frac{\left(\omega+k\omega_t\right)^2}{4k^2\omega_s}\Big) \end{equation}where $\omega_s=\frac{q^2_z}{2k^2}\big( \sigma^2_{tt}-\cfrac{K_{yt}a_4+K_{xt}a_3}{a_2}+ \cfrac{C_{Rx}a^2_3}{a_2\left(a_2+C_{Rx}\left(C_{Ry}+\sigma^2{yy}\right)\right)} +A\big(\vec V_1,\vec V_2\big) \big)$ – coefficient determining DS broadening; $\omega_t= \cfrac{\left(K_{xy}K_{yt}+\left(C_{Ry}+\sigma^2_{yy}\right)K_{xt}\right)\left(\cos\psi-\cos\chi\right)} {\left( \sigma^2_{xx}+C_{Rx}\right) \left( C_{Ry}+\sigma^2_{yy}\right)-K^2_{xy}}+ [0.5pc]$ $D\left( \vec V_1, \vec V_2 \right)$ – coefficient that determines the offset of the center frequency of the DS;
\begin{eqnarray*} A\left( \vec V_1, \vec V_2\right) = \end{eqnarray*}\begin{eqnarray*} \frac{C_{Rx}\left( C_{VRy}C_{Ry}K_{xy}-C_{VRx}a_2\right) \left( 2a_3+C_{VRy}C_{Ry}K_{xy}-C_{VRx}a_2\right) } {a_2\left( a_2+C_{Rx}\left( C_{Ry}+\sigma^2_{yy}\right) \right) } + \end{eqnarray*} \begin{eqnarray*} \frac{C_{Ry}C_{VRy}\left( a_1C_{VRy}+2a_4\right) }{a_2} -\frac{2a_v}{q^2_z}, \end{eqnarray*} \begin{eqnarray*} D\left( \vec V_1, \vec V_2\right) = \end{eqnarray*} \begin{eqnarray*} -R'_x \frac{C_{Ry}C_{VRy}K_{xy}\left(\displaystyle{\frac{a_2 + 2C_{Rx}\left(C_{Ry} + \sigma^2_{yy}\right)}{a_2}}\right)}{a_2+C_{Rx}\left(C_{Ry}+\sigma^2_{yy}\right)} - \end{eqnarray*} \begin{eqnarray*} - \frac{C_{VRx}\left(C_{Ry}+\sigma^2_{yy}\right)C_{Rx}}{a_2+C_{Rx}\left(C_{Ry}+\sigma^2_{yy}\right)} \end{eqnarray*}
$V_t$ – terms arising from the velocity of movement of the receiver and transmitter;
\begin{eqnarray*} C_{VRy} = V_y \left( \frac{R_{02}} {R_{01}}+\frac{Vr_y} {V_y}\right) \big/ \left(\frac{R_{02}} {R_{01}} +1 \right) \end{eqnarray*},
\begin{eqnarray*} C_{VRx}= V_x \left( \frac{R_{02}} {R_{01}}+\frac{Vr_x \sin^2 \chi} {V_x \sin^2 \psi}\right) \big/ \left( \frac{R_{02}} {R_{01}} +\frac{\sin^2 \chi}{sin^2 \chi} \right), \end{eqnarray*} \begin{eqnarray*} a_v = \frac{-1.38 sin^2 \psi}{R^2_{01}\delta^2_{xt}}\left( V_x\right) ^2- \frac{1.38\left( V_y\right) ^2}{R^2_{01}\delta^2_{yt}} - \end{eqnarray*} \begin{eqnarray*} \frac{1.38 \sin^2 \chi}{R^2_{02}\delta^2_{xr}}\left( Vr_x\right)^2 - \frac{1.38\left( Vr_y\right) ^2}{R^2_{02}\delta^2_{yr}}, \end{eqnarray*} \begin{eqnarray*} V_t=\cos \psi V_x - \cos \chi Vr_x - \sin \chi Vr_z - \sin \psi V_z, \end{eqnarray*} \begin{eqnarray*} R'_x = \cos \psi - \cos \chi, \quad q_z = -k \left( sin \psi + \sin \chi \right), \end{eqnarray*} \begin{eqnarray*} a_1=\sigma^2_{xx}\sigma^2_{yy} - K^2_{xy}, \end{eqnarray*} \begin{eqnarray*} a_2=\sigma^2_{xx}\left( C_{Ry}+\sigma^2_{yy}\right) -K^2_{xy}, \end{eqnarray*} \begin{eqnarray*} a_3 = K_{xy}K_{yt}+\left( C_{Ry}+ \sigma^2_{yy}\right) K_{xt}, \end{eqnarray*} \begin{eqnarray*} a_4 = K_{xy}K_{xt} + K_{yt} \sigma^2_{xx}; \end{eqnarray*} \begin{eqnarray*} C_{Rx} = \frac{\displaystyle{\frac{\delta^2_{xr}}{5.52} \left( \frac{R_{02}}{R_{01}} + \frac{\sin^2 \chi}{\sin^2 \psi}\right)^2 }} {\displaystyle{\left( \frac{R^2_{02} \delta^2_{xr}}{R^2_{01}\delta^2_{xt}} + \frac{\sin^2 \chi}{\sin^2 \psi} \right) \left( 1+ \frac{\sin \chi}{\sin \psi} \right)^2}} \end{eqnarray*}and
\begin{eqnarray*} C_{Ry} = \frac{\displaystyle{\frac{\delta^2_{yr}}{5.52 \sin^2 \psi} \left( \frac{R_{02}}{R_{01}} + 1 \right)^2 }} {\displaystyle{ \left( \frac{R^2_{02} \delta^2_{yr}}{R^2_{01}\delta^2_{yt}} + 1\right) \left( 1+ \frac{\sin \chi}{\sin \psi} \right)^2 } } \end{eqnarray*}– the coefficients that determine the effective AP of the receiver, which describes the distribution of the field intensity on the water surface and, for example, in the case of equal distances to the receiver and the transmitter $ R_{02} = R_{01}$, the same antennas of the receiver and the transmitter $ \delta^2_{yr} = \delta^2_{yt}$, $ \delta^2_{xr} = \delta^2_{xt}$, and the same grazing angles of the receiver and the transmitter $\psi = \chi$, the coefficients take the following forms: $C_{Rx} = \delta^2_{xr} / 11.04$, $C_{Ry} = \delta^2_{yr} / \left( 11.04 \sin^2 \psi \right)$; $V^2_{eff}$ – effective reflection coefficient. In the case of only smooth large-scale irregularities, the reflection coefficient (Fresnel coefficient) is written as follows [Bass and Fuks, 1979]:
\begin{eqnarray*} V^{HH}_{eff} \left( \psi, \chi \right) = \frac{\cos \Theta - \sqrt{\varepsilon-\sin^2\Theta}}{\cos \Theta +\sqrt{\varepsilon-\sin^2\Theta}}, \end{eqnarray*} \begin{eqnarray*} V^{VV}_{eff} \left( \psi, \chi \right) = \frac{\varepsilon \cos \Theta - \sqrt{\varepsilon-\sin^2\Theta}}{\varepsilon\cos \Theta +\sqrt{\varepsilon-\sin^2\Theta}} \end{eqnarray*}–for electromagnetic waves of horizontal and vertical polarization, $\varepsilon$ – complex dielectric constant of a water surface; It should be noted that $\Theta = 90^{\circ} - (\psi + \chi) / 2$ is the local angle of incidence on the specular reflecting site. In the monostatic case when the receiver and the transmitter are in the same place – $\Theta = 0^{\circ}$. In this paper, all calculations will be given for the vertical polarization of the emitted and received electromagnetic waves. It should be noted that under sea conditions the reflection coefficient depends on the intensity of the small-scale component of the wave spectrum. To take this effect into account, instead of the Fresnel coefficient, we introduce the concept of the effective reflection coefficient; $\sigma^2_{xx}$ and $\sigma^2_{yy}$ – the slope variances of large-scale waves, in comparison with the radiation wavelength along the $X$-axis and along the $Y$-axis, respectively; $\sigma^2_{tt}$ – vertical orbital velocity variance; $K_{xt}$ and $K_{yt}$ – correlation coefficients of slopes and vertical orbital velocity; $K_{xy}$ – the correlation coefficient of slopes along the $X$ and $Y$ axes.
The width of the DS at the level of $-10$ dB is:
\begin{eqnarray*} \Delta f_{10} = 4 \sqrt{\omega_s \ln10} / \lambda = \end{eqnarray*} \begin{eqnarray*} \frac{\sqrt{2\ln10}}{\pi} \times \end{eqnarray*} \begin{eqnarray*} \Bigg(q^2_z \left( \sigma^2_{tt} - \frac{K_{yt}a_4 +K_{xt}a_3}{a_2} + \right. \end{eqnarray*} \begin{equation} \tag*{(2)} \bigg. \frac{C_{Rx}a^2_3}{a_2 \left( a_2 + C_{Rx}\left( C_{Ry}+ \sigma^2_{yy}\right) \right) } + A \left( \vec{V_1}, \vec{V_2} \right) \bigg) \Bigg)^{1/2} \end{equation}The width of the DS is caused by the spread in the velocities of the observed reflecting sites. In the case of fixed carriers, the maximum possible variance of the observed velocities is equal to the vertical orbital velocity variance $\sigma^2_{tt}$, which can be achieved only in the absence of a correlation between the slopes and the vertical orbital velocity $K_{xt}$ and $K_{yt}$, which means that each reflector with any slope of the surface has a velocity variance equal to $\sigma^2_{tt}$. With an increase in the correlation of the slopes and the vertical orbital velocity, the observed velocity spread decreases until it turns to zero, as, for example, in the case of a sinusoidal surface (with a narrow effective AP), where there is a rigid connection between the reflector slope and its velocity.
The shift of the DS in Hz will be expressed as follows:
\begin{eqnarray*} f_{sh} = - \frac{\omega_t}{\lambda} = \frac{-1}{\lambda} \times \end{eqnarray*} \begin{eqnarray*} \left( \frac{( K_{xy}K_{yt} + ( C_{Ry} + \sigma^2_{yy}) K_{xt} ) ( \cos \psi - \cos \chi ) } {( \sigma^2_{xx} + C_{Rx} ) ( C_{Ry} + \sigma^2_{yy}) - K^2_{xy}} + \right. \end{eqnarray*} \begin{equation} \tag*{(3)} \Bigg. D ( \vec{V_1}, \vec{V_2}) \Bigg) \end{equation}The DS shift is determined by the average speed of the observed reflective sites. At the same angles of radiation and observation $\psi = \chi$, it is determined only by the speed of movement of the carriers since the mathematical expectation of the vertical orbital velocity is 0.
The scattering cross-section, calculated as the integral of DS (1) over frequency and is expressed as follows:
\begin{eqnarray*} \sigma_0=\cfrac{\left|V^2_{eff}\right|}{2\cos^4\cfrac{\psi-\chi}{2}}\times \end{eqnarray*} \begin{equation} \tag*{(4)} \frac{\exp\left(\cfrac{-\tan^2\dfrac{\psi-\chi}{2}\left(C_{Ry}+\sigma^2_{yy}\right)}{2\left(\big(\sigma^2_{xx}+C_{Rx}\big)\left(C_{Ry}+\sigma^2_{yy}\right)-K^2_{xy}\right)}\right)}{\sqrt{\big(\sigma^2_{xx}+C_{Rx}\big)\left(C_{Ry}+\sigma^2_{yy}\right)-K^2_{xy}}} \end{equation}The scattering cross-section is determined by the number of observed reflective sites. As can be seen from formula (4), the scattering cross-section decreases with an increase in the slope variance and reaches its maximum value at $\psi = \chi$.
In formulas (3) and (4) the AP of the antenna in the corresponding plane is always added to the slope variances of the reflecting surface. This makes it possible to retrieve the slope variances from the measurements of the DS shift (3) or the scattering cross-section (4) using at least two antenna systems with different AP [Titchenko and Karaev, 2019].
The characteristics of DS (2), (3) and (4) fully describe the model DS (1) and will be investigated further in this work. Surface parameters in this work will be calculated using the wave spectrum model from [Karaev et al., 2008; Ryabkova et al., 2019], for fully developed wind waves and a radiation wavelength of 23 cm (L-band).
Let us consider the measurement scheme for the case of receiving the reflected GNSS signal on a stationary offshore platform. Let us take the velocity of the navigation satellite in the earth-centered, earth-fixed reference system (ECEF): $V_x = 2523$ m/s, $V_y = 361$ m/s, $V_z = 1163$ m/s, $V_{r_x} = V_{r_y} = V_{r_z} = 0$ m/s; distance from the center of AP footprints on the sea surface to the transmitter and receiver: $R_{01} = 20000000$ m, $R_{02} = 100$ m. It should be noted that in this case where the distance to the transmitter is much greater than the distance to the receiver, the effective AP is determined only by the receiving antenna and does not depend on the transmitter antenna.
 |
| Figure 2 |
The dependence of the DS characteristics (2), (3) and (4) on the direction of wave propagation at various receiving AP is shown in Figure 2.
It can be seen from the figure that the DS shift is determined only by the speed of the satellite and does not depend on the wave parameters and the AP. It is also seen that the scattering cross-section decreases with an increase in the AP of the receiving antenna and has an azimuthal dependence when using an asymmetric AP. The DS width, on the contrary, grows with an increase in the AP of the receiving antenna and has an azimuthal dependence. The weak azimuthal dependencies of the DS width and the scattering cross-section when using a wide antenna are explained by the distortion of the AP footprint when the receiving antenna is tilted. Using azimuthal measurements of the DS width and scattering cross-section, it is possible to determine the direction of wave propagation with an uncertainty of $180\mbox{°}$.
 |
| Figure 3 |
Further, in Figure 3, we consider the dependencies of the DS characteristics on the azimuthal direction of the navigation satellite for a fixed direction of wave propagation $\varphi = 0$.
The satellite velocity module in the azimuth plane is 2550 m/s. The direction of the navigation satellite velocity $0\mbox{°}$ corresponds to the movement of the satellite in the $Y=0$ plane in the positive direction of the $X$ axis with velocities $V_x = 2550$ m/s, $V_y = 0$ m/s. The direction of $90\mbox{°}$ corresponds to the movement of the satellite with velocities $V_x =0$ m/s, $V_y = 2550$ m/s. The wave propagates along the $X$ axis. The Figure also shows the effect of the vertical velocity $V_z$ of the navigation satellite on the characteristics of the reflected signal. It can be seen from the figure that the navigation satellite velocity does not affect the scattering cross-section and width of the DS, which will be convenient for determining the direction of wave propagation. The DS shift, on the contrary, is sensitive to changes in the direction of the satellite velocity and to its vertical speed, and at the same time is not sensitive to the AP, which, in combination with insensitivity to the direction of wave propagation (see Figure 2), can be used to determine the navigation satellite velocity relative to the ground.
 |
| Figure 4 |
Let us consider the case of a fixed grazing angle of the receiver $\chi = 60\mbox{°}$ and the flight over it of the navigation satellite in Figure 4. In this case, the grazing angle of the transmitter will change during the passage of the satellite. The figure shows the dependencies for different receiving AP and different azimuthal angles of wave propagation.
The figure shows that the scattering cross-section weakly depends on the wave direction in the case of using a wide AP, and the sensitivity to the grazing angle of the transmitter for a wide receiving AP is also much lower than that for a narrow AP. The DS width, on the contrary, is insensitive to changes in the wave propagation angle with a narrow receiving AP, whereas with a wide AP, a dependence on the wave propagation angle appears, while the DS width also increases with increasing AP. The DS shift turns to 0 at $\sim65.5\mbox{°}$, which means that at this grazing angle the sum of the projections of the vertical and horizontal velocities on the sensing axis is 0. Knowing the speed of the navigation satellite, the measurement of the DS shift will allow monitoring the grazing angle of the transmitter.
In this paper, for the first time, a complete analytical formula for the DS (1) of the reflected signal is presented in the bistatic formulation of the problem. When calculating, you can set the velocity of movement of the transmitter and receiver, grazing angles, and consider the AP. The formula for the DS depends on 6 statistical parameters of waves, which can be retrieved when solving the inverse problem.
The bistatic formulation of the problem expands the range of applicability of the quasi-specular scattering model for sensing the sea surface in comparison with the monostatic one.
The paper considers the case of signal emission by a navigation satellite and reception of radiation reflected by the water surface on a stationary offshore platform by a fixed receiver. As a result, it was shown that in this scheme, by measuring the characteristics of the DS, the azimuthal angle of wave propagation with an uncertainty of $180\mbox{°}$ can be determined when using receiving antennas with asymmetric AP.
For sensing from space, a scheme can be applied using existing navigation satellites as transmitter and receiver on a small spacecraft.
In comparison with the most popular method for calculating the characteristics of reflected signals from navigation satellites [Zavorotny and Voronovich, 2000], the method considered in this paper does not require the use of a wave spectrum model. On the one hand, this makes it possible to calculate the characteristics of the Doppler spectrum using known or measured by other methods wave parameters, for example, using an underwater acoustic wave gauge [Titchenko and Karaev, 2013] or using spacecraft, for example, in the GPM mission [Panfilova et al., 2018]. On the other hand, in the DS formula, there is an explicit connection between the characteristics of the reflected signal and the wave parameters, which opens possibilities for retrieving these wave parameters from the DS measurements.
Bass, F. G., I. M. Fuks (1979) , Scattering of Waves by Statistically Rough Surfaces, 540 pp., Pergamon Press, Oxford.
Cardellach, E., F. Fabra, O. Nogués-Correig, at al. (2011) , GNSS-R ground-based and airborne campaigns for ocean, land, ice, and snow techniques: Application to the GOLD-RTR data sets, Radio Sci., 46, p. RS0C04, https://doi.org/10.1029/2011rs004683.
Clarizia, M. P., C. P. Gommenginger, S. T. Gleason, M. A. Srokosz, C. Galdi, M. Di Bisceglie (2009) , Analysis of GNSS-R delay-Doppler maps from the UK-DMC satellite over the ocean, Geophys. Res. Lett., 36, p. L02608, https://doi.org/10.1029/2008gl036292.
Fateev, V. F., A. V. Ksendzuk, P. S. Obukhov, et al. (2012) , Multi-position radar system with synthesized antenna aperture based on reflected signals from GNSS "GLONASS", Electromagnetic Waves and Electronic Systems, no. 17, p. 62–68 (in Russian).
Gleason, S. (2006) , Remote sensing of ocean, ice and land surfaces using bistatically scattered GNSS signals from low earth orbit, Thesis, University of Surrey, Guildford, UK.
Hobiger, T., R. Haas, and J. S. Löfgren (2014) , GLONASS-R: GNSS reflectometry with a frequency division multiple access-based satellite navigation system, Radio Sci., 49, p. 271–282, https://doi.org/10.1002/2013rs005359.
Jing, C., X. Niu, C. Duan, X. Niu, C. Duan (2019) , Sea Surface Wind Speed Retrieval from the First Chinese GNSS-R Mission: Technique and Preliminary Results, Remote Sens., 11, p. 3013, https://doi.org/10.3390/rs11243013.
Kanevskii, M. B., V. Y. Karaev (1996) , Spectral characteristics of a microwave radar signal backscattered by the sea surface at small incidence angles, Radiophys Quantum Electron, 39, p. 347–352, https://doi.org/10.1007/bf02124686.
Karaev, V., M. Kanevsky, E. Meshkov (2008) , The effect of sea surface slicks on the Doppler spectrum width of a backscattered microwave signal, Sensors, 8, p. 3780–3801, https://doi.org/10.3390/s8063780.
Karaev, V. Y., Y. A. Titchenko, E. M. Meshkov, M. A. Panfilova, M. S. Ryabkova (2019) , Doppler spectrum of microwave signal backscattered by sea surface at small incidence angles, Sovremennye Problemy Distantsionnogo Zondirovaniya Zemli iz Kosmosa, 16, p. 221–234, https://doi.org/10.21046/2070-7401-2019-16-6-221-234 (in Russian).
Martin-Neira, M. (1993) , A Passive Reflectometry and Interferometry System (PARIS): Application to ocean altimetry, ESA journal, no. 17, p. 331–355.
Panfilova, M. A., V. Y. Karaev, J. Guo (2018) , Oil Slick Observation at Low Incidence Angles in Ku-Band, Journal of Geophysical Research: Oceans, 123, p. 1924–1936, https://doi.org/10.1002/2017JC013377.
Ruf, C., P. Chang, M. P. Clarizia, S. Gleason, et al. (2016) , CYGNSS Handbook, 154 pp., Michigan Publishing, University of Michigan, Ann Arbor, MI.
Ryabkova, M., V. Karaev, J. Guo, Y. Titchenko (2019) , A Review of Wave Spectrum Models as Applied to the Problem of Radar Probing of the Sea Surface, Journal of Geophysical Research: Oceans, 124, p. 7104–7134, https://doi.org/10.1029/2018jc014804.
Sakhno, I. V., E. A. Tkachev, D. A. Gavrilov, et al. (2009) , Small spacecraft for sea surface survey using signals from satellite radio navigation systems, Journal of Instrument Engineering, no. 52, p. 34–39 (in Russian).
Titchenko, Y. A., V. Y. Karaev (2013) , The method of determining the sea-wave parameters by using a modified acoustic wave gauge, Radiophys Quantum El, 55, p. 493–501, https://doi.org/10.1007/s11141-013-9385-5.
Titchenko, Y. A., V. Y. Karaev (2016) , Peculiarities of a modified model of spectral and energy characteristics of scattered waves considering the emitting and receiving antenna patterns for bistatic sensing of the sea surface , Sovremennye Problemy Distantsionnogo Zondirovaniya Zemli iz Kosmosa, 13, no. 2, p. 67–83, https://doi.org/10.21046/2070-7401-2016-13-2-67-83 (in Russian).
Titchenko, Y., V. Y. Karaev, M. S. Ryabkova, et al. (2017) , The method for solving the inverse problem of bistatic remote sensing of the sea surface with moving receiver and transmitter, 2017 Progress in Electromagnetics Research Symposium - Fall (PIERS - FALL), IEEE, Singapore, https://doi.org/10.1109/PIERS-FALL.2017.8293619.
Titchenko, Y., V. Y. Karaev (2018) , Doppler Spectrum of Microwaves at Forward Scattering from the Sea Surface, Igarss 2018–2018 Ieee International Geoscience and Remote Sensing Symposium, IEEE, Valencia, Spain, https://doi.org/10.1109/IGARSS.2018.8517326.
Titchenko, Y., V. Y. Karaev (2019) , New Opportunities for Multistatic Remote Sensing Of Water Surface Using Receivers with Different Antenna Patterns, IGARSS 2019 - 2019 IEEE International Geoscience and Remote Sensing Symposium, IEEE, Yokohama, Japan, https://doi.org/10.1109/IGARSS.2019.8898859.
Valenzuela, G. R. (1978) , Theories for the interaction of electromagnetic and oceanic waves – A review, Boundary-Layer Meteorol, 13, p. 61–85, https://doi.org/10.1007/BF00913863.
Zavorotny, V. U., A. G. Voronovich (2000) , Scattering of GPS signals from the ocean with wind remote sensing application, IEEE Transactions on Geoscience and Remote Sensing, 38, no. 2, p. 951–964, https://doi.org/10.1109/36.841977.
Zavorotny, V. U., S. Gleason, E. Cardellach, et al. (2014) , Tutorial on Remote Sensing Using GNSS Bistatic Radar of Opportunity, IEEE Geoscience and Remote Sensing Magazine, 2, no. 4, p. 8–45, https://doi.org/10.1109/MGRS.2014.2374220.
Received 19 April 2020; accepted 28 October 2020; published 14 November 2020.


Citation: Titchenko Yu. A. (2020), Bistatic Doppler spectrum of radiation reflected by a water surface, Russ. J. Earth Sci., 20, ES6007, doi:10.2205/2020ES000745.
Copyright 2020 by the Geophysical Center RAS.