RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 20, ES6004, doi:10.2205/2020ES000727, 2020
D. G. Yarakhanova1, M. E. Hossain2
1Kazan Federal University, Kazan, Russian Federation
2Department of Petroleum and Energy Engineering, American University, Cairo, Egypt
When designing the development of hydrocarbon fields for efficient production, it is necessary to correctly position horizontal wells. Specific solutions are required for optimal placement of horizontal well systems. An algorithm is proposed to select the optimal development option for systems with horizontal wells. Mathematical models of non-traditional collectors are presented. The proposed block diagram of the algorithm of actions will make it possible to choose the best option for developing a field with systems of horizontal wells. A complex model allows one to obtain true (or real) initial data for their subsequent processing in the modeling process and to obtain results that are as close to reality as possible.
An algorithm for finding the optimal option for field development is proposed with systems of horizontal wells. Petroleum industry has established itself as the pioneer of subsurface data collection [Abou-Kassem, 2006]. Historically, no other discipline has taken so much care in making sure input data is as accurate as the latest technology would allow. The recent superflux of technologies dealing with subsurface mapping, real time monitoring, and high speed data transfer is an evidence of the fact that input data in reservoir simulation are not the weak link of reservoir modeling.
Mathematical models made a significant contribution towards finding a solution for the problems associated with the usage of horizontal wells.
Current standard modelling approaches conceptualize a fractured media as an interplay of several homogeneous continuums of normal diffusive characteristics. The precise characterization of the fractures is imperative for well performance analysis along with subdiffusive behaviour of unconventional matrices such as crystalline basement reservoirs.
This study research presents a study of some of the available models that are used in modelling of fractured reservoirs.
In modelling, reservoir simulation is the most powerful tool for oil and gas reserves estimation as well as reservoir performance prediction. However, serious limitations exist at the very foundation of reservoir simulation when it comes to unconventional reservoirs.
Difficulties exist from data acquisition to applicability of Darcy's law and solution techniques that are applicable only to conventional reservoirs. Behaviour of flow through matrix and fractured systems in the same reservoir, heterogeneity and fluid/rock properties interactions, Darcy and non-Darcy flow are among the issues that are needed to be thoroughly addressed.
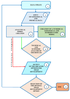
Around the globe oil and gas fields are often developed using horizontal wells. They are used chaotically. When designing the development of an oil field with horizontal wells, the question arises of how best to locate the horizontal wells for efficient field development. There is an infinite number of options available for developing this particular object with various options for placing horizontal wells, and it depends on a large number of factors.
 |
| Figure 1 |
In order to find a better way to a solution for this problem, an algorithm is proposed for solving the choice of the optimal development option for horizontal well systems, a block diagram of which is shown in Figure 1.
Step 1. Beginning of the algorithm. Updating data.
Step 2. Input operation. Input of the initial geological and physical data of the simulated field.
Step 3. Data processing. Creation of an analytical model for a preliminary assessment and determination of the desired search zone with a preliminary arrangement of options for the placement of horizontal well systems.
Step 4. Data processing. Creation of a numerical hydrodynamic model to clarify the acceptable parameters of the development system.
Step 5. Iterative process. Technical and economic analysis of the results.
Step 6. Output of results. Conclusion of the obtained development options using systems horizontal wells.
Step 7. Search cycle. Selection of the optimal field development option using systems horizontal wells that satisfies the geological and mathematical model of the field.
Step 8. Completion of the program. The end of the algorithm.
It is possible to move (green arrow) from Step 3 to Step 5 to clarify the created analytical model by means of technical and economic analyzes of the results.
It is possible to conduct an express analysis by going (red arrow) from Step 3 to Step 6.
In order to improve and refine the final results of Step 7, you need to go to Step 1 and update the data.
For the first time, an algorithm for determining the optimal field development option using systems is proposed of horizontal wells. The scientific novelty of this research is that this algorithm will provide the most realistic option for field development using horizontal well systems. When using systems of horizontal well systems, there will be a cumulative effect of production growth and greater drainage coverage.
Mathematically speaking, a horizontal well is a large fracture of finite length [Yarakhanova, 2015].
Currently available approximate methods for assessing the productivity of horizontal wells do not give accurate results.
Often, horizontal wells open unconventional reservoirs. Knowing the properties of an unconventional fractured reservoir, we can draw an optimal trajectory of horizontal wells.
Cracks can be created artificially by using hydraulic fracturing.
 |
| Figure 2 |
As you know, the goal of hydraulic fracturing is to create cracks to ensure fluid flow to the bottom of the well. The effectiveness of the operation depends on the correct selection of the facility for operations, the selection of technologies for existing conditions and the reasonable selection of wells for processing. The selection, placement of horizontal wells and optimization of fracture parameters for hydraulic fracturing should be carried out taking into account the geological and physical properties of the object, stress distribution in the reservoir, which determines the orientation of the fractures and the waterflooding system. During the development of hydrocarbons from unconventional reservoirs, horizontal well systems and hydraulic fracturing are used [Yarakhanova, 2015, 2019]. Sequential hydraulic fracturing in one wellbore can significantly increase the area of development of the developed formation, increase the flow rate of the well (presented in Figure 2). There is an opportunity to draw into development reserves that are classified as hard to recover in deposits with low permeability. Increasing the number hydraulic fracturing is not an end in itself; it is necessary to select an economically viable oil production method for each specific field [Yarakhanova, 2019].
If we will be well aware of the properties of a fractured reservoir, we will be able to develop it as efficiently as possible and to position horizontal wells correctly. Consider mathematical models of unconventional reservoirs.
Hydraulic fractures is not an end in itself; it is necessary to select an economically viable oil recovery method for each specific field [Yarakhanova, 2019].
If we are well aware of the properties of a fractured reservoir, we will be able to develop it as efficiently as possible and correctly position horizontal wells. Consider mathematical models of unconventional reservoirs.
To describe the hydrodynamic processes in fractured-porous media, it is taken into account that a horizontal well in mathematical terms is a large fracture of finite length. This can be used in mathematical models for subsequent efficient trajectories layout of horizontal wells and further assessment them of the productivity.
The comprehensive model is translated into a mathematical form that can be easily used to describe fluid flow in porous media.
This study will help to better understand the modelling of fractured reservoirs including hydrocarbon traps in a crystalline basement.
In reservoir simulation, the principle of GIGO (Garbage in and garbage out) is well known [Rose, 2000]. This principle implies that the input data should be accurate for the simulation results to be acceptable.
Currently, three major approaches are used to simulate fluid flow through naturally fractured reservoirs which include: continuum, dual porosity/dual permeability, and flow through discrete fracture approaches. In single continuum approach fractured medium is divided into a number of representative volumes and bulk macroscopic values of reservoir properties varying from point-to point are averaged over the volume which is often known as blocked based permeability tensors [Reiss, 1980; Park, 2001]. Gupta, et al. [2001] considered matrix with no permeability and simulated fluid flow through fractures only. Park [2001] considered matrix and fractures as a continuous system and ignored the fluid flow at fracture matrix interface.
Some researchers [Gupta, et al., 2001; Park, et al., 2000; Teimoori, et al., 2005] on the other hand present comprehensive methodologies for estimating permeability tensor for arbitrarily oriented and interconnected fracture systems. In the dual continuum approach, the reservoir is divided into two major parts: fractures and matrix.
Warren and Root [1963] model conceptualizes fractured reservoirs with a stacked sugar cubes. In this approach, the fractures provide the main flow paths, while the matrix acts as a source of fluid. The fluid transfer between the fractures and the significant number of studies have been carried out both in analytical and numerical frameworks using dual porosity approach. Landereau et al., [2001] and Henn et al., [1999] proposed a new technique for matrix is defined based on transfer functions. Henn et al., [1999] and Landereau, et al., [2001] introduced a range of different matrix/fracture transfer functions to simulate the fluid flow on large scales. Then the fluid flow is simulated in a fractured porous medium, for example, in rock massifs. The proposed technique has been created to separate the contributions from the rock matrix and from the fracture systems (which are also treated as an equivalent continua), the so-called dual (double) porosity models, dual (double) permeability models and dual (double) continuum models, in order to simplify the complexity in the fracture-matrix interaction behavior and to partially consider the size effects caused mainly by the fractures.
It has been shown that the advective transport component in more permeable matrix blocks (e.g., porous sandstones) results in additional solute transfer between fractures and matrix, which is not typically taken into account by dual porosity concepts [Cortis and Birkholzer, 2008].
Therefore, Noetinger and Estebenet [2000] proposed a new technique called continuous time random walk (CTRW) method. This method is an alternative to the classical dual porosity models for modelling and upscaling flow and/or solute transport in fractured rock masses.
Originally developed to describe electron hopping in heterogeneous physical systems, the network of fractures become more complicated when there are vugs present in addition to fractures. Fractures and vugs can have profound effects on the porosity exponent ($m$) and calculated water saturation ($S_{w}$) of carbonate rocks.
Proper prediction of $m$ in reservoirs avoid overestimation of $S_{w}$ commonly caused by the presence of fractures and also avoid the underestimation of $S_{w}$ commonly caused by vuggy or moldic porosity. The original dual porosity equation, developed by Aguilera and corrected in [Aguilera and Aguilera, 2003] is as follows
\begin{eqnarray*} \phi_{m} = \frac{\log \left(\phi_{f}^{m_{f}} + \frac{1-\phi_{f}^{m_{f}}}{\acute{\phi_{b}}^{-m_{b}} }\right)}{\log{\phi}} , \end{eqnarray*}where $\acute{\phi}_{b}$ according to Aguilera, is the matrix block porosity affected by $m_{f}$ and is defined by the equations
\begin{eqnarray*} \acute{\phi}_{b} = \left(\phi - \phi_{f}{^{f}}\right)/\left(1-\phi_{f}{^{f}}\right) \end{eqnarray*}and
\begin{eqnarray*} f = m_{f} - \left(m_{f} - 1 \right) \left(\log{\phi} / \log{\phi_{f}} \right) \end{eqnarray*}direction, which is rarely the case. Since fractures inclined to current would give straight-line conductance paths as opposed to the tortuous paths in the bulk porosity, $m_{f}$ should usually blow but not necessarily 1.0.
The triple porosity for vugs and fractures together can be written as:
\begin{equation} \tag*{(1)} 1 - \acute{\phi_{v}} = \left[\frac{\phi_{bv}^{m_{bv}}}{\phi_{b}^{m_{b}}}\right]^{\frac{1}{m_{v}}} \frac{\phi_{bv}^{-m_{bv}}-1}{\phi_{b}^{-m_{b}}-1} , \end{equation}where
$\acute{\phi_{v}} = \phi_{v} / \left(1 - \phi_{f}\right), \phi_{bv} = \phi_{v} + \phi_{b}\left(1 - \acute{\phi_{v}}\right), $
$m_{bv}$ is the composite porosity exponent. The following modified
\begin{eqnarray*} \phi_{m} = \frac{\log \left( \phi_{f} + \frac{1 - \phi_{f}}{\phi_{b}^{-m_{b}}} \right)}{\log \phi}, \end{eqnarray*}where $\phi_{m}$ is the total porosity, $\phi_{b}$ is the porosity of the bulk rock, $m_{b}$ is the porosity exponent of the bulk rock, and $\phi_{f}$ is the fracture porosity in relation to the total volume. The value of fracture $m$ ($m_{f}$) is not used and is implicitly assumed to be 1.0. It means that the fractures are assumed to contribute in parallel to the whole rock conductivity. The use of parallel resistance implies that the fractures themselves are parallel to the current equation (1) was then used on the results:
\begin{eqnarray*} \phi_{f} = \frac{\phi^{\frac{m}{m_{f}}-m} \phi_{bv}^{m_{bv}} - \phi^{\frac{m}{m_{f}}}}{\phi_{bv}^{m_{bv}}-1}. \end{eqnarray*}For a modeling process to be meaningful, it must fulfill two criteria, namely, the source has to be true (or real) and the subsequent processing has to be true [Islam, et al., 2017; Islam, et al., 2016a].
For unconventional reservoirs as well as crystalline basement reservoirs, they are both of concern.
For instance, most commonly used well log data do not register useful information for unconventional reservoirs that do not allow invasion of sonic signals, mud filtrate, etc., invalidating some of the well logging techniques.
Processing data is also of concern.
Unconventional reservoirs require special filtering tools that are not readily available. Some of them are presented in our previous book chapters [Islam, et al., 2017].
 |
| Figure 3 |
 |
| Table 1 |
Various Mathematical Models to Describe the Fluid Flow and Change of Fluid Volume in porous Media with Fracture are described below in Table 1 and presented in Figure 3.
Various options for selecting the optimal field development option using horizontal well systems are proposed:
The proposed algorithm makes it possible to choose the optimal option for field development using horizontal well systems, taking into account the geological structure and hydrocarbon reserves with constant updating of the incoming initial geological and physical data of the simulated area.
Abou-Kassem, J. H., S. M. Farouq-Ali, M. R. Islam (2006) , Petroleum Reservoir Simulations: A Basic Approach, 445 pp., Gulf Publications Co., Houston, Texas.
Aguilera, R., M. S. Aguilera (2003) , Improved Models for Petrophysical Analysis of Dual Porosity Reservoirs, Petrophysics, 44, no. 1, p. 21–35.
Baker, W. J. (1955) , Flow in Fissured Reservoir, Thesis, 4th World Petroleum Congress, Rome, Italy.
Cortis, A., J. Birkholzer (2008) , Continuous Time Random Walk Analysis of Solute Transport in Fractured Porous Media, Water Resources Research, 44, https://doi.org/10.1029/2007WR006596.
DeSwaan, H. (1975) , Analytical Solution for the Determination of Naturally Fractured Reservoir Parameters by Well Testing, Thesis, SPE Western Regional Meeting, Ventura, California.
Gupta, A., et al. (2001) , Crystal structure of Rv2118c: an AdoMet-Dependent Methyltransferase from Mycobacterium Tuberculosis H37Rv, Journal of Molecular Biology, 312, no. 2, p. 381–91, https://doi.org/10.1006/jmbi.2001.4935.
Henn, N., B. Bourbiaux, M. Quintard, et al. (1999) , Modelling Conductive Faults With a Multiscale Approach Involving Segregation Concept, 10th European Symposium on Improved Oil Recovery, https://doi.org/10.3997/2214-4609.201406362.
Islam, M. R., S. H. Hossain, S. H. Moussavizadegan, et al. (2016) , Advanced Petroleum Reservoir Simulation: Towards Developing Reservoir Emulators, 592 pp., Scrivener Publishing LLC, https://doi.org/10.1002/9781119038573.
Islam, M. R., M. E. Hossain, A. O. Islam (2017) , Hydrocarbons in Basement Formations, 642 pp., Scrivener Publishing LLC, Salem, Massachusetts, https://doi.org/10.1002/9781119294498.
Islam, M. R., J. S. Islam, et al. (2016a) , The Greening of Pharmaceutical Engineering, 482 pp., Scrivener Publishing LLC, https://doi.org/10.1002/9781119159704.
Kazemi, H. (1969) , Pressure Transient Analysis of Naturally Fractured Reservoir With Uniform Fracture, Society of Petroleum Engineers Journal, 9, no. 4, https://doi.org/10.2118/2156-A.
Landereau, P., B. Noetinger, M. Quintard (2001) , Quasi-Steady Two-Equation Models for Diffusive Transport in Fractured Porous Media: Large-Scale Properties for Densely Fractured Systems, Advances in Water Resources, 24, no. 8, p. 863–876.
Metzler, R., W. G. Glöckle, T. F. Nonnenmacher (1994) , Fractional Model Equation for Anomalous Diffusion, Physica A: Statistical Mechanics and its Applications, 211, no. 1, p. 13–24, https://doi.org/10.1016/0378-4371(94)90064-7.
Nie, R., Y. Meng, Y. Jia, et al. (2012) , Dual Porosity and Dual Permeability Modeling of Horizontal Well in Naturally Fractured Reservoir, Transport in Porous Media, 92, p. 213-235, https://doi.org/10.1007/s11242-011-9898-3.
Noetinger, B., T. Estebenet (2000) , Up-Scaling of Double Porosity Fractured Media Using Continuous-Time Random Walks Methods, Transport in Porous Media, 39, p. 315–337, https://doi.org/10.1023/A:1006639025910.
Park, C. C. (2001) , The Environment: Principles and Applications, 660 pp., Routledge, London, UK.
Park, H., J. Choe, J. Kang (2000) , Pressure Behavior of Transport in Fractal Porous Media Using a Fractional Calculus Approach, Energy Sources, 22, no. 10, p. 881–890, https://doi.org/10.1080/00908310051128237.
Raghavan, R. (2011) , Fractional Derivatives: Application to Transient Flow, Journal of Petroleum Science and Engineering, 80, no. 1, p. 7–13, https://doi.org/10.1016/j.petrol.2011.10.003.
Reiss, L. H. (1980) , The Reservoir Engineering Aspects of Fractured Formations, 108 pp., Editions TECHNIP, Paris, France.
Rose, W. (2000) , Myths About Later-Day Extensions of Darcy's Law, Journal of Petroleum Science and Engineering, 26, no. 1–4, p. 187–198, https://doi.org/10.1016/S0920-4105(00)00033-4.
Teimoori, A., Z. Chen, S. S. Rahman, T. Tran (2005) , Effective Permeability Calculation Using Boundary Element Method in Naturally Fractured Reservoirs, Petroleum Science and Technology, 23, no. 5–6, p. 693–700, https://doi.org/10.1081/LFT-200033029.
Warren, J. E., P. J. Root (1963) , The Behavior of Naturally Fractured Reservoir, Society of Petroleum Engineers Journal, 3, no. 3, p. 245–255, https://doi.org/10.2118/426-PA.
Yarakhanova, D. G. (2015) , The Feasibility of Drilling Horizontal Wells, Thesis, EAGE, Moscow, Russia.
Yarakhanova, D. G., et al. (2019) , Horizontal Wells and Multistage Hydraulic Fracturing, Drilling and Oil, no. 10, p. 27–28.
Received 23 January 2020; accepted 28 July 2020; published 29 October 2020.


Citation: Yarakhanova D. G., M. E. Hossain (2020), Algorithm for selecting systems horizontal wells and mathematical models for unconventional reservoirs, Russ. J. Earth Sci., 20, ES6004, doi:10.2205/2020ES000727.
Copyright 2020 by the Geophysical Center RAS.