RUSSIAN JOURNAL OF EARTH SCIENCES, VOL. 15, ES2003, doi:10.2205/2015ES000551, 2015
V. P. Tsvetkov, I. V. Tsvetkov
Tver State University, Tver, Russia
.In this work the model of variations of average annual temperature of the Northern Hemisphere of the Earth is constructed. On its basis, in this research, the main regularities of temporary variability of temperature over the period from 1000 to 2010 have been revealed with the help of application of methods of multi-fractal dynamics. Over the period of 1010 years there were founded 26 periods and for each of them a value of fractal dimension of $D$ was settled. Also, the function of jumps of difference $h=D - D_0$ (where $D_0$ is an equilibrium value of fractal dimension) describing the dynamics of fractal dimension for the period under consideration was constructed. The question of correlation of a historical process and behavior of function $h$ has been discussed.
One of the most important climatic characteristics of the Earth is an average annual ground temperature dynamics, in particular of the Northern hemisphere where the greater part of the population resides. The temperature regime exerts powerful influence on activity both of an individual and catholic humanity. In connection with this, study of long-term changes of temperature regimes of the Earth is of the most immediate interest for different human areas.
At the present time, the global warming tendency and its consequences are being studied intensively [Houghton, 2001]. Nevertheless, not least important is a question of average annual ground temperature dynamics of the Earth on more extended time intervals, more specifically throughout the previous millennium [Houghton, 2001]. The instrumental world temperature measurements began about 150 years ago, and a pre-existent temperature regime is now being evaluated by the means of less precise instrumental controls [NASA, 2013]. On the basis of such indirect data verified in comparison with data of thermometers, it became possible to establish the temperature mode in the Northern hemisphere of the Earth over the period from the XI century up to the present moment.
It is evident that temperature dynamics analysis and forecast are possible when using mathematic models. The fundamentally new possibilities in this regard can be given by the multifractal dynamics model (MFD) [Kudinov et al., 2011]. Thus, on the basis of the MFD model, in the research [Kudinov et al., 2012] there were studied the tendencies of global warming over the period from 1850 to date. It turned out that this time interval is spitted into 5 periods lasting from 30 to 31 year, at a fractal dimension of a global temperature curve as follows: $D \in (1.140, 1.202)$. The prediction estimates of the MFD model with a linear trend [Kudinov et al., 2012] concerning the temperature rise by 2072, shall be equal to 0.5° C which confirms the tendencies of global warming in the near future. Somewhat different is follows from the MFD model with a linear trend [Kudinov et al., 2012]. So, we can see slight growth of a global temperature by 0.04° C by 2024.
The purpose of this work is investigation of the major regularity of temporal variability of temperature of the Northern hemisphere over a period of 1000–2011 on the basis of the MFD model. Among these are determination of $D_i$ values of corresponding time intervals $T_i$, equilibrium values of fractal dimension $D_0$ and coefficients describing the influence of these external thermal sources on the earth atmosphere temperature. According to the MFD model, the fugacity of temperature difference $(h = D - D_0)$ plays a major role in description of the dynamics of ground temperature variations. We shall investigate $h$ function behavioristic characteristics over the last 1011 years and demonstrate its association with historical processes.
The connection of a temperature regime and human mental performance was reported by Ch. Lombrozo [2006].
L. Chizhevsky [1924] contributed to revelation of connections of cosmic factors and the epochal flow.
 |
| Figure 1 |
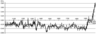
In connection with the relevance of studying of changes of surface temperature and factors influencing it, in 1988 the World Meteorological Organization (WMO) and the United Nations Environment Programme (UNEP) founded the special organization – The Intergovernmental Panel on Climate Change (IPCC). Its main objective is the assessment of risks of the global climate change caused by technogenic factors (human activity). In the report dated 2001 the IPCC managed to restore the range of values of fluctuation of average surface temperature in the Northern hemisphere observed over the period from 1000 with 95 percent [Houghton, 2001]. In this work the average values of temperature fluctuations from the specified range in the 2nd and the beginning of the 3rd millennium were used. On the basis of data [Houghton, 2001; NASA, 2013], the chart of fluctuations of average annual surface temperature of the Northern hemisphere of the Earth and its piecewise and linear trend covering the period from 1000 to 2011 is constructed. This chart is given in Figure 1.
In this work, fluctuation of temperature of the Northern hemisphere of the Earth $v$ near equilibrium value $v_0=15$° C has been considered.
From Figure 1 it is seen that the most values of surface temperature of the Northern hemisphere were on the average 0.25° C lower than the average annual temperature of $v_0=15$° C observed over the period from 1000 to 1927. At that, the trend was steadily below the abscissa axis until 1933. Then, from 1933 to 2011, the value of average annual temperature grew by 0.8° C.
Consequently, the tendencies of global warming have started being shown since 1933. This event can be connected with the influence of human factors (deforestation and other changes of landscapes, pollution of atmosphere and reservoirs in connection with increase in human production activity, etc.).
In consonance with the MFD model [Kudinov et al., 2011; Kudinov et al., 2012], let us approximate function $v$ by the piecewise linear trend on each area
\begin{equation} \tag*{(1)}\label{1} v=\overline{v}+\tilde{y}(t), \end{equation}where $\overline{v}$ is a linear part, and $\tilde{y}$ is fast oscillations in relation to a trend.
At that, $\overline{v}$ has a fractal dimension equal to 1, and $\tilde{y}$ - equal $1$ $(1 \leq D \leq 2)$. The approximation accuracy on interval T will be defined in C-metrics
\begin{eqnarray*} \triangle ={\mathop{\max }_{t_0\le t\le T} \left|\tilde{y}(t)\right| }. \end{eqnarray*}In the MFD model, a linear trend on the time interval $i$ is as follows:
\begin{equation} \tag*{(2)}\label{2} \overline{v}_i(t)=\overline{v}_{oi}(t_{oi})+X_i(D_i)(t_i-T_{oi}),1 \leq i \leq N. \end{equation}Let us call the equilibrium value of fractal dimension as $D_0$, whereby $X(D_0) = 0$. In this condition, the linear trend of temperature is a constant. Let us call $h=D-D_0$ .
Further, let us consider only small deviation of $D$ from $D_0$. Then
\begin{equation} \tag*{(3)}\label{3} X(D) = -\eta h + O(-h)^2 \end{equation}Coefficient $\eta$ from (3) describes the influence of external thermal sources on temperature of the atmosphere of the Earth.
 |
| Table 1 |
With the calculations given above we have obtained the values of parameters $N, T_i, X_i, h, D_i, D_0,\eta_i$ provided in Table 1.
Note that 26 half-cycles, or 13 periods lasting from 41 to 132 years were identified over the period of 1011 years. The values of fractal dimension $D$ obtained are given in Table 1, at that, the maximum fractal dimension value is noted on the 15th interval – $D=1.312$, and the minimum one – on the 8th interval – $D=1,181$. It should be noted that the value of $D$ is less than the Gaussian value of $D$ = 1.5 what is indicative of the determined nature of the processes responsible for dynamics of temperature.
Parameter $X$, which characterizes the main tendency of changes (the direction and speed) of the average annual temperature of a surface of the Northern hemisphere, is equal $\mathrm{ 0.01 \mbox{°} C yr^{-1}}$, on the average.
Table 1 is also gives the values of coefficient $\eta $ which is in the range from 0.02 to $\mathrm{ 0.895 \mbox{°} C yr^{-1}}$. Such fluctuation of $\eta $ testifies that in different intervals of time the degree of impact of various thermal sources on temperature of the Northern hemisphere of the Earth was various.
Equilibrium $D_0$ value of fractal dimension which is approximately equal 1.2 for all intervals, except for 14 and 15 when $D_0$ possess value 1.255 is also given in Table 1. On this interval, the most significant fall of temperature of the Northern hemisphere to $v = -0.6$° C during the considered period was observed.
Thus, the interval of supervision over fluctuations of the average annual surface temperature of the Northern hemisphere of the Earth from 1000 to 2011 has been managed to be broken into $T_{i} \left(i{\mathrm = 1, 2, 3,... ,26}\right)$ half-cycles and ${\check{T}}_i (i{\mathrm =1, 2, 3,\dots , 13)}$ periods on which curve $v(t)$ under consideration has a certain value of fractal dimension $D_i\left(i{\mathrm =1, 2, 3, ..., 26}\right)$. At that, speed $X_i (i=$1,2,3, ..., 26) of linear trend ${\overline{v}}_i(t)$ approximating set function $v(t)$ in the $t^{th}$ period, depends only on $D_i$ in the constructed model.
 |
| Figure 2 |
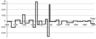
On the basis of Table 1, the chart of jumps of difference of $h = D - D_0$ completely reflecting the nature of dynamics of variations of the surface temperature of the Northern hemisphere of the Earth in the 2-nd and the beginning of the 3rd millennium is constructed. It is given in Figure 2.
The values of function $h$ are characterized by the extent of escape of the temperature trend from the equilibrium value when it is constant.
From Figure 2, it is possible to notice that the greatest value of function of jumps of difference $h$ was recorded over the 1333 to 1352 period. On this time interval $h$ possess value 0.067 (in Table 1, $i=9$), and in this period (Figure 1) a considerable fluctuation of the average annual temperature in negative direction (in 1350 the value becomes equal to $v=-0.48$° C) can be observed. Here the analogy with one of the periods of abnormally low activity of the Sun can be drawn: 1280–1350 – the Wolf minimum.
Similarly, since 1468, considerable climate change mitigation in the territory of the Northern hemisphere ($h=-0.053$, $v=0.09$° C) can observed, and since 1487 and before the end of the period under consideration is out, we can see considerable lowering of the average annual temperature ($h$ practically reaches value 0.06, and the average annual temperature deviation during this period becomes $v =-0.6$° C.
Thus, over the 1468 to 1497 period we can see the biggest jump of function $h$ from value -0.053 to nearly 0.06, that is we have $h=0.113$. This period is also simultaneous with abnormally low activity of the Sun observed over the 1450 to 1550 period (Shperer Minimum).
Thus, 13 full waves (rise–drop) were revealed for 1011 years. The periods of the greatest fluctuations of function $h$ are simultaneous with abnormally low activity of the Sun–Shperer and Wolf Minimums.
Using Figure 2, the question of correlation of the historical process and average annual surface temperature can be considered. Owing to the complexity and ambiguity of historical events recorded over the 1000 to 2011 period under consideration in the territory of the Northern hemisphere of the Earth, these events can be categorized (for example: wars, plague and cholera pandemic, mass persecutions of Jews, etc.) [Chizhevsky, 1924].
 |
| Figure 3 |
 |
| Figure 4 |
 |
| Figure 5 |
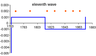
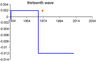
Let us consider the examples of plague and cholera pandemic in relation to the plot of function $h$. Figure 3, Figure 4. and Figure 5 present examples of plots of $h$ together with an indication of dates considered as the beginning of advance of plague and cholera.
The distribution percent for this category in relation to {$h > 0.002$} has been calculated; this corresponds to a negative half wave and a positive one with a very small amplitude value. Such approach is connected with small errors in computing $h$ on the basis of data on indirect observation of temperature values.
 |
| Table 2 |
The calculation results are presented in Table 2.
There were only 2 cases of plague and cholera pandemic occurred at $h > 0.002$ in every ten. These are the second and the fifth waves. For them we have $h=0.004$ and 0.065, respectively.
Thus, we can see the significant prevalence of contraction of mass diseases of cholera and plague in the periods where $h > 0.002$. In the same way, the social activity can be considered.
In this paper we present a piecewise linear trend of an average annual ground temperature of the Earth as of from 1000 to 2011, using the MFD model. We have defined 26 time intervals each of which demonstrates a temperature regime sufficiently close to the evidential one. And the conclusion from this are 13 cyclical periods lasting from 41 to 132 years.
On all time intervals, the values of fractal dimension $D$ which vary within the range of $1.181 \geq D \geq 1.312$ has been calculated. The maximum value of $D$ belongs to the 15th interval, and the minimum one – to the 8th interval. These results highlight the sufficiently deterministic nature of processes responsible for the ground temperature dynamics over the last millennium.
The rate of ground temperature linear trend change $X$ over the same period has been measured over the following range of values: $-0.209 \geq X \geq \geq 0.197$° C. The maximum linear trend falling speed observed was $X = 0.209$° C, and the maximum rate of growth was $X=0.197$° C on the 10th and 26th intervals, correspondingly.
Equilibrium value $D_0$ of the fractal dimension is within the range of $1.195 \geq D_0 \geq 1.255$ what, in turn, suggests stability of the values obtained. Let us note an applicable maximum value $D_0$ on the 14th and 15th intervals where the maximum temperature decrease of $-0.6$° C was observed.
The $\eta $ coefficient values are in the range of $0.102 \geq \eta \geq 0.895 \mbox{°} \mathrm{ C yr^{-1}}$, what is indicative of a great variability of thermal sources having a bearing upon a ground temperature.
The $h$ function behavior analysis performed demonstrates a doubtless connection of its behavior with the Sun's activity defined by the Wolf numbers.
The question of correlation and stochastic behavior of the process and behavior of function $h$ has been considered by the example of plague and cholera. The major predominance of initiation of diseases is observable over the period when $h \geq 0.02$.
Correlation of behavior of $h$ with other historical events will be considered in our follow-up works.
Houghton, J. T., Y. Ding, D. J. Griggs, et al. (2001), Climate Change 2001: The Scientific Basis. Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change, 881 pp., Cambridge University Press, Cambridge, United Kingdom and New York, USA.
NASA, (2013), GISS Surface Temperature Analysis: Annual Mean Temperature Change for Hemispheres, NASA, Goddard, USA, http://data.giss.nasa.gov/gistemp/graphs_v3/, 12 February 2013.
Kudinov, A. N., V. P. Tsvetkov, I. V. Tsvetkov (2011), Catastrophes in the Multi-Fractal Dynamics of Social-Economic Systems, Russian Journal of Mathematical Physics, 18, no. 2, p. 149–155, doi:10.1134/S1061920811020038.
Kudinov, A. N., O. I. Krylova, V. P. Tsvetkov, I. V. Tsvetkov (2012), Global warming in mathematical model of multifractal dynamics, Russian Journal of Earth Sciences, 12, p. ES3001, doi:10.2205/2012ES000510.
Lombroso, C. (2006), The Man of Genius, 400 pp., Kessinger Publishing , Whitefish, Montana.
Chizhevsky, A. L. (1924), The physical factors of the historical process, 72 pp., 1st Gostipolitografiya, Kaluga.
Received 27 May 2015; accepted 29 May 2015; published 8 June 2015.


Citation: Tsvetkov V. P., I. V. Tsvetkov (2015), Analysis of a piecewise linear trend of average surface temperature in the mathematical model of multifractal dynamics, Russ. J. Earth Sci., 15, ES2003, doi:10.2205/2015ES000551.
Copyright 2015 by the Geophysical Center RAS.