Scattering of VLF field at a three-dimensional ionospheric...

4. Numerical Calculation Results

Figure 2

[23] As a result of the performed calculations, a series of regularities in the behavior of the amplitude and phase of the attenuation function V( R) at the presence of a local irregularity at the upper wall of the Earth-ionosphere waveguide is found. It was assumed at calculations that the source and receiver are located on the Earth's surface: z=z_t=0. The emitting frequency of the dipole was chosen to be f=20 kHz. The height of the regular waveguide and its impedance were obtained using the vertical profiles of the concentration N_e(z) and collision frequency n_e(z) of electrons shown in Figure 2. The geomagnetic field was assumed to correspond to the mid-European conditions (in the vicinity of the point with coordinates 47^o N and 18^o E). The impedances of the base S_p and side surface S_l of the irregularity cylinder were chosen equal to d_p=0.5(1+i)10^-2 and d_l=0.5(1-i)10², respectively [Soloviev and Hayakawa, 2002]. The dimensions of the cross section of the cylinder (described by the formula [(x-x_p)/a_p]²+ [(y-y_p)/b_p]²=1, its height z_p, and location relative to the propagation path (shown in Figure 2 by arrows) determined by the coordinates of the ellipse center x_p and y_p were varied. Along the path 01500 km the amplitude and phase of the attenuation function were calculated for the cases of various path orientation relative to the geomagnetic field vector, properties of the underlying surface, and location and geometric dimensions of the irregularity ( a_p, b_p, and z_p ).

Figure 3

Figure 4

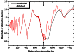
[24] Figures 3 and 4 show the amplitudes and phases of the attenuation function for the nighttime period. The distance from the source to the receiver in kilometers is shown at the x axis. The underlying surface is wet soil with a relative dielectric permeability of e_m=20 and conductivity of s=0.01 S m^-1. The radio wave propagation direction is chosen along the south-north line (the azimuth is A_z=0 ). The following parameters of the irregularity are chosen: a_p=b_p=20 km and z_p=20 km. In Figure 3 the irregularity is put directly over the signal propagation path ( y_p=0 ) in the region of the minimum of the attenuation function amplitude at the regular path ( x_p=800 km). At such choice of the coordinates, the effects related to the presence of the irregularity are best pronounced. It is demonstrated in Figure 4.

[25] No graphs of the amplitude and phase of the attenuation function for the daytime are presented in the paper. Soloviev and Hayakawa [2002] showed that such irregularities weakly distort the field in the daytime Earth-ionosphere waveguide. Moreover, the sprites modeled here are observed mainly at night.

[26] Below we consider the amplitude deviations: the difference in the attenuation function amplitude values in the undisturbed and disturbed by a three-dimensional irregularity cases. There exists an influence of the irregularity on the behavior of the attenuation function phase, but it is less important than the influence on the amplitude behavior. Since the graphs showing the phase changes are not such visual as the graphs showing the amplitude changes, the former are not presented.

Figure 5

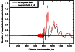
[27] Figure 5 shows the curves of amplitude disturbances corresponding to the cases when the geomagnetic field is and is not taken into account. The curves differ considerably from each other, so one may conclude that taking into account of the magnetic field is important. One can see in Figure 5 and the following figures the presence of not only forward scattering but backscattering as well.

Figure 6

Figure 7

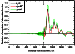
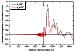
[28] The perturbations in the attenuation function amplitude illustrating the influence of the irregularity on the field as a function of the propagation direction relative the magnetic azimuth of the path are shown in Figures 6 and 7. The strongest difference is seen between the field behavior at the paths with the azimuth A_z=90^o and A_z=-90^o, the former and the latter azimuths corresponding to the eastward and westward propagation, respectively. The change of the wave propagation direction to the opposite one ( A_z=45^o and A_z=225^o ) is shown in Figure 7. It is worth noting that the presence of the irregularity influences these paths in a different way.

Figure 8

Figure 9

Figure 10

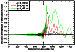
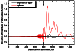
[29] Figures 8, 9, and 10 show the influence of the geometric dimensions of the irregularity on the attenuation function amplitude. Figure 8 shows curves corresponding to various values of the semiaxes of the cylinder base of the irregularity. The large and small semiaxes of ellipse are taken to be equal ( a_p=b_p ) and to have values of 10 km, 20 km, and 40 km. It is worth noting that a change of the radius of the cylinder base by a factor of 2 leads to a change in the maximum disturbance in the attenuation function amplitude approximately by the same factor.

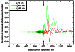
[30] The influence of the cylinder height is shown in Figure 9. The values of the impedances of the base and sidewall of the cylinder stayed fixed. The comparison of the changes caused by the irregularity in the form of a cylinder with impedance of the base d_p=0.5(1+i)10^-2 and by the irregularity of a "spot" type with impedance d_p=(2.38 -i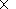 times 0.34)10^-2 (obtained by recalculation to the waveguide height by the method described above) is shown in Figure 10. Comparing the curves one can conclude that taking into account of the possibility of a descent (assent) of the local region of the waveguide upper wall relative to the level of the regular ionosphere plays an important role in the study of the irregularity impact on radio wave propagation.

Figure 11

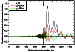
[31] Figure 11 illustrates the fact that the influence of the irregularity on the field in the waveguide depends also on the location of the irregularity relative to the radio wave propagation path. Figure 11 shows the curves corresponding to the distance of the cylinder axis from the path line equal to y_p = 0, y_p = 20, and y_p = 50 km for a_p=b_p=20 km and x_p=800 km. At relatively short distances between the irregularity and path (~50 km), a decrease of the maximum disturbance in the attenuation function amplitude by a factor of more than 10 is observed. It should be noted here that for the considered path, one can estimate the distance by the lateral dimension of the first Fresnel's zone, the small semiaxes of the latter being ~53 km.

Figure 12

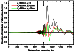
[32] The position of the observer influences considerably the estimate of the changes caused by the presence of the irregularity. A shift in the coordinates of the observational point actually corresponds to a shift in the irregularity location along and across the radio wave propagation path. The same shift in the direction lateral to the path would cause much stronger changes in the irregularity impact than a shift along the path. This dependence is shown in Figure 12.

Figure 13

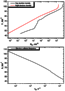
[33] The influence of the underlying surface properties is shown in Figure 13. The curves are shown corresponding to the following underlying surfaces: wet soil ( e_m=20, s = 0.01 S m^-1 ) and seawater ( e_m=81, s = 4 S m^-1 ). Figure 13 shows the graph calculated at the value of the propagation path magnetic azimuth A_z=0. It is worth noting that stronger influence of the irregularity is observed if a sea is the underlying surface than if waves propagate over a land. At other orientation of the wave propagation path, the character of the amplitude perturbations is the same.