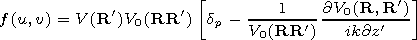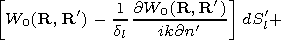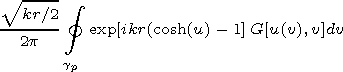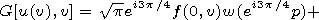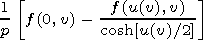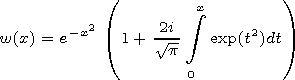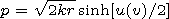3. Principal Equations
[17] Using the second Green formula one can obtain an expression
for function
P(r,j,z) in any point of the
D region via the
integral over the irregularity surface
Sp  Sl:
Sl:
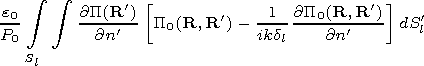 | (2) |
where
R(r,j,z) Sp, Sl denotes the observational point,
R'(r',j',z') Sp, Sl corresponds to the integration point,
n' is the
normal directed outside the wave volume,
P0( R) is the field of the initial
source in a regular waveguide with a thickness of
h and homogeneous
walls with the impedances
dg and
di, and
P0( R, R') is the Green
function. The expression for the latter may be obtained from the formula for
P0( R) substituting
r by
r1=(r2+ r'2 - 2rr' cos(j-j'))1/2 and
zt by
h (see Figure 1). In the limiting case
R
Sp, Sl corresponds to the integration point,
n' is the
normal directed outside the wave volume,
P0( R) is the field of the initial
source in a regular waveguide with a thickness of
h and homogeneous
walls with the impedances
dg and
di, and
P0( R, R') is the Green
function. The expression for the latter may be obtained from the formula for
P0( R) substituting
r by
r1=(r2+ r'2 - 2rr' cos(j-j'))1/2 and
zt by
h (see Figure 1). In the limiting case
R  Sp, Sl in the right-hand side of
equation (2), there appears an extra term of the form
P( R)/2, this fact
being related to the jump in the normal derivative of the Green function
Sp, Sl in the right-hand side of
equation (2), there appears an extra term of the form
P( R)/2, this fact
being related to the jump in the normal derivative of the Green function
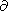 P0( R', R)/
P0( R', R)/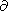 n'.
n'.
[18] This very choice of the Green function
P0( R, R') in the form of a
solution for the regular waveguide makes it possible to limit the region of
integration in equation (2) down to the dimensions of the irregularity
surfaces
Sp and
Sl. The method of construction of an approximate
solution of equation (2) with the accuracy up to the terms of the order of
O((kr)-1) was described in detail by
Soloviev [1998].
The condition of its
applicability is
kr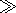 1 (that is, the observational point should be located in
the wave zone from the source). There is no additional conditions, for
example, on the dimensions of the irregularity. In this paper we describe
only the main stages of the solution of equation (2).
1 (that is, the observational point should be located in
the wave zone from the source). There is no additional conditions, for
example, on the dimensions of the irregularity. In this paper we describe
only the main stages of the solution of equation (2).
[19] Two-dimensional equation (2) is solved by asymptotic
transformation into an one-dimensional one. To do that we reveal the
quickly oscillating multiplier and introduce the attenuation function
If one introduces the ecliptic coordinates
equation (2) for attenuation function would have the form
[20] When
kr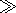 1, the exponential multiplier in the first integral becomes
quickly changing in the direction transverse to the propagation circuit on the
background of the multiplier left under the integral.
1, the exponential multiplier in the first integral becomes
quickly changing in the direction transverse to the propagation circuit on the
background of the multiplier left under the integral.
[21] The latter makes it possible to perform the calculation of the integral in
terms of
dv over the cylinder base by the stationary phase method. As a
result the integral in terms of variable
v, which may be considered as a
curvature integral along the irregularity boundary. The contour of integration
is passed clockwise. Thus, with an accuracy up to the terms of the order of
O((kr)-1), we obtain the expression for the attenuation function
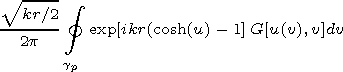 | (3) |
where
[22] To solve equation (3), we use the numerical-analytical method of
semi-inversion
[Soloviev and Agapov, 1997],
which combines the direct
inversion of the dominant part of the integral operator of the problem, that is
a Volterra operator, with the iterative process by which the remaining part
of the integral operator is inverted through successive approximations. The
influence of the side surface of the cylindrical irregularity
Sl is taken into
account
by convertional stepwise procedure.
Below, all the results of
numerical calculations are presented for the attenuation function
V( R).
This
function physically demonstrate the difference of the field in the waveguide
with a three-dimensional irregularity from the dipole field over an ideally
conducting surface.

Powered by TeXWeb (Win32, v.2.0).
 Sl:
Sl:
 Sl:
Sl:
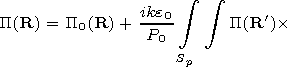
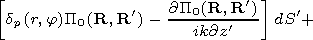
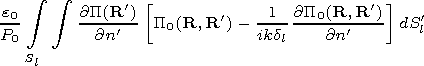
 Sp, Sl corresponds to the integration point,
n' is the
normal directed outside the wave volume,
P0( R) is the field of the initial
source in a regular waveguide with a thickness of
h and homogeneous
walls with the impedances
dg and
di, and
P0( R, R') is the Green
function. The expression for the latter may be obtained from the formula for
P0( R) substituting
r by
r1=(r2+ r'2 - 2rr' cos(j-j'))1/2 and
zt by
h (see Figure 1). In the limiting case
R
Sp, Sl corresponds to the integration point,
n' is the
normal directed outside the wave volume,
P0( R) is the field of the initial
source in a regular waveguide with a thickness of
h and homogeneous
walls with the impedances
dg and
di, and
P0( R, R') is the Green
function. The expression for the latter may be obtained from the formula for
P0( R) substituting
r by
r1=(r2+ r'2 - 2rr' cos(j-j'))1/2 and
zt by
h (see Figure 1). In the limiting case
R  Sp, Sl in the right-hand side of
equation (2), there appears an extra term of the form
P( R)/2, this fact
being related to the jump in the normal derivative of the Green function
Sp, Sl in the right-hand side of
equation (2), there appears an extra term of the form
P( R)/2, this fact
being related to the jump in the normal derivative of the Green function
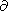 P0( R', R)/
P0( R', R)/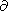 n'.
n'.
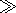 1 (that is, the observational point should be located in
the wave zone from the source). There is no additional conditions, for
example, on the dimensions of the irregularity. In this paper we describe
only the main stages of the solution of equation (2).
1 (that is, the observational point should be located in
the wave zone from the source). There is no additional conditions, for
example, on the dimensions of the irregularity. In this paper we describe
only the main stages of the solution of equation (2).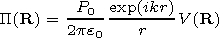
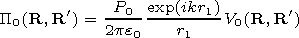
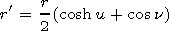

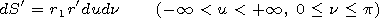



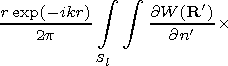
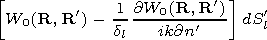
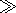 1, the exponential multiplier in the first integral becomes
quickly changing in the direction transverse to the propagation circuit on the
background of the multiplier left under the integral.
1, the exponential multiplier in the first integral becomes
quickly changing in the direction transverse to the propagation circuit on the
background of the multiplier left under the integral.