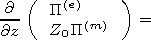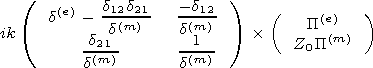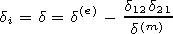2. Formulation of Electrodynamical Problem of Scattering
[12] The problem of the field of a harmonic ( exp(-i wt ))
vertical electric dipole
in the Earth-ionosphere waveguide with a three-dimensional local
irregularity is considered in the impedance formulation for the parallel-plain model of
the waveguide channel. The published estimates of the vertical and
horizontal dimensions of sprites modeled by our local irregularity show that
the dimensions do not exceed 50-100 km. This means that the
electromagnetic field scattered at such irregularity may be considerable (and
thus may be observed and registered) only at short paths of
~1000-1500 km
for which one can neglect the curvature of the Earth's surface. The
neglecting by the Earth's curvature makes the problem visual not breaking
the general character of the proposed solution algorithm. A transition to the
spherical model may be done using the formulae obtained by
Soloviev [1990] and
Soloviev and Agapov [1997].
In the considered model of the
waveguide, the lower wall described by a plain surface
Sg is assumed
to be homogeneous, its properties being determined by the surface
impedance
dg.
The waveguide is limited from the top by the surface
Si, its
properties being determined (in its regular part) by the impedance
di. The
three-dimensional local irregularity directly adjoining the upper wall of the
waveguide is chosen in the form of a finite by a height cylinder, the shape of
the cross section of it being arbitrary. The surface of the upper wall of the
cylinder coincides with the surface
Si, whereas the surface of the lower
wall
Sp is located in the plane parallel to the surface
Si.
We will denote
the side surface of the cylinder as
Sl. The properties of the waveguide
space
D  R3 limited by the waveguide walls and surfaces of the model
irregularity coincide with the properties of the vacuum, its dielectric and
magnetic permeability and wave number being
e0,
m0, and
k,
respectively.
R3 limited by the waveguide walls and surfaces of the model
irregularity coincide with the properties of the vacuum, its dielectric and
magnetic permeability and wave number being
e0,
m0, and
k,
respectively.
|
|
Figure 1
|
[13] In the cylindrical coordinate system
(r, j,z) with the
z axis going
through the source, the surfaces
Sg and
Si are described by the equations
z=0 and
z=h,
respectively. The source of the field (a vertical electrical
dipole with the dipole moment
P0 ) is located in the point
(0,0,zt ). The
surface
Sp
lies in the plane
z=zp,
and the surface
Sl is parallel to the
z axis. The problem geometry is shown in Figure 1.
In a scalar approximation
(neglecting field depolarization at the scatter at the three-dimensional
irregularity) the electromagnetic field excited by such source is described by
the vertical component of the Hertz vector which in the
D region
satisfies the inhomogeneous Helmholtz equation and the following boundary
conditions:
 | (1) |
where
n is the external normal to the boundary surfaces of the waveguide
volume,
d(M)=dg for
M  Sg,
d(M)=di for
M
Sg,
d(M)=di for
M  Si,
d(M)=dl for
M
Si,
d(M)=dl for
M  Sl,
and
d(M)=dp(r, j) for
M
Sl,
and
d(M)=dp(r, j) for
M  Sp.
Conditions at the infinity
require attenuation of
P(r, j, z) at
r
Sp.
Conditions at the infinity
require attenuation of
P(r, j, z) at
r 
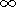 .
In this case there is no need to
attract additionally a boundary condition at the edge (the line of crossing of
Sp and
Si,
Sp,
and
Sl ) because the available conditions guarantee
unambiguousness of the solution. It should be noted that actually in the VLF
range, there are the following estimates of the impedance values for the TM
polarization field generated by the considered source:
|dg,i,p|<1 and
|dl|>1.
If the vertical component of the Hertz vector is known, the vertical
component of the electric field may be calculated by
.
In this case there is no need to
attract additionally a boundary condition at the edge (the line of crossing of
Sp and
Si,
Sp,
and
Sl ) because the available conditions guarantee
unambiguousness of the solution. It should be noted that actually in the VLF
range, there are the following estimates of the impedance values for the TM
polarization field generated by the considered source:
|dg,i,p|<1 and
|dl|>1.
If the vertical component of the Hertz vector is known, the vertical
component of the electric field may be calculated by
[14] For determination of the values of the parameters of the inhomogeneous
impedance model of the waveguide channel Earth-ionosphere, we
attracted known from publications
[Orlov et al., 2000]
vertical profiles of
the concentration
Ne(z) and effective collision frequency
ne(z) of
electrons. For the given frequency and angle of incidence of the
electromagnetic wave at an inhomogeneous layer
Y, the equation for the
impedance matrix
is integrated numerically from a height of ~100 km downward to
~40 km,
covering with a guaranty the region important for formation of the
reflected from the ionosphere VLF field
[Galiuk et al., 1989;
Kirillov, 1979,
1981].
We take the determination of the impedance in the form
Etg= Z0di[ Htg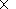 n],
where
Z0 =(m0/e0)1/2, and
Etg and
Htg are the
tangential to the considered surface components of the electric and magnetic
fields, respectively. The values
di= dd of the impedance matrix
components obtained at the lower boundary of integration
z=zd are
recalculated to the height
z=h in the vacuum. The formulae for such
recalculation we obtain using the following matrix of the reflection index of
the plane wave
on the boundary of the plasma semispace in vacuum on the vertical
coordinate
n],
where
Z0 =(m0/e0)1/2, and
Etg and
Htg are the
tangential to the considered surface components of the electric and magnetic
fields, respectively. The values
di= dd of the impedance matrix
components obtained at the lower boundary of integration
z=zd are
recalculated to the height
z=h in the vacuum. The formulae for such
recalculation we obtain using the following matrix of the reflection index of
the plane wave
on the boundary of the plasma semispace in vacuum on the vertical
coordinate
Substituting the relation of the reflection index and surface impedance matrix
at the plasma semispace-vacuum boundary
where
into the expressions for the components of the impedance matrix, we obtain
formulae for recalculation of the components of the impedance matrix to the
height
z=h in vacuum
where
[15] The height
z=h corresponds to the altitude where the combination of the
impedance matrix
d= d(e) - d12 d21/ d(m) in a minimum way depends on
the angle
Y.
For realization of such algorithm together with the equation for
the matrix
di,
the equation for its derivative
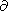 di/
di/ 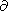 Y,
is integrated. Also
the formulae of recalculation of the derivative in vacuum were derived and
used. The value of the Earth's surface impedance
dg is determined by the
given values of the relative dielectric permeability and conductivity for the
two-layer model of the underlying surface.
Y,
is integrated. Also
the formulae of recalculation of the derivative in vacuum were derived and
used. The value of the Earth's surface impedance
dg is determined by the
given values of the relative dielectric permeability and conductivity for the
two-layer model of the underlying surface.
[16] In this paper we are not interested in what degree the initial TM
field at the scatter at the irregularity will be reexcited into the field of the TE
polarization. We will assume this effect to be negligible. So the anisotropy
related to the presence of the geomagnetic field will be approximately taken
into account. It is known that in a general case the TM and TE components
of the electric field are described by the electric
P(e) and magnetic
P(m) Hertz vectors and are related. For the field in the vacuum cavity this relation
is expressed by the following boundary conditions at the ionospheric wall of
the waveguide:
So the impedance we use in the scalar problem is taken in the form

Powered by TeXWeb (Win32, v.2.0).
 R3 limited by the waveguide walls and surfaces of the model
irregularity coincide with the properties of the vacuum, its dielectric and
magnetic permeability and wave number being
e0,
m0, and
k,
respectively.
R3 limited by the waveguide walls and surfaces of the model
irregularity coincide with the properties of the vacuum, its dielectric and
magnetic permeability and wave number being
e0,
m0, and
k,
respectively. R3 limited by the waveguide walls and surfaces of the model
irregularity coincide with the properties of the vacuum, its dielectric and
magnetic permeability and wave number being
e0,
m0, and
k,
respectively.
R3 limited by the waveguide walls and surfaces of the model
irregularity coincide with the properties of the vacuum, its dielectric and
magnetic permeability and wave number being
e0,
m0, and
k,
respectively.

 Sg,
d(M)=di for
M
Sg,
d(M)=di for
M  Si,
d(M)=dl for
M
Si,
d(M)=dl for
M  Sl,
and
d(M)=dp(r, j) for
M
Sl,
and
d(M)=dp(r, j) for
M  Sp.
Conditions at the infinity
require attenuation of
P(r, j, z) at
r
Sp.
Conditions at the infinity
require attenuation of
P(r, j, z) at
r 
 .
In this case there is no need to
attract additionally a boundary condition at the edge (the line of crossing of
Sp and
Si,
Sp,
and
Sl ) because the available conditions guarantee
unambiguousness of the solution. It should be noted that actually in the VLF
range, there are the following estimates of the impedance values for the TM
polarization field generated by the considered source:
|dg,i,p|<1 and
|dl|>1.
If the vertical component of the Hertz vector is known, the vertical
component of the electric field may be calculated by
.
In this case there is no need to
attract additionally a boundary condition at the edge (the line of crossing of
Sp and
Si,
Sp,
and
Sl ) because the available conditions guarantee
unambiguousness of the solution. It should be noted that actually in the VLF
range, there are the following estimates of the impedance values for the TM
polarization field generated by the considered source:
|dg,i,p|<1 and
|dl|>1.
If the vertical component of the Hertz vector is known, the vertical
component of the electric field may be calculated by
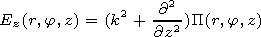
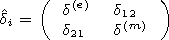
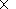 n],
where
Z0 =(m0/e0)1/2, and
Etg and
Htg are the
tangential to the considered surface components of the electric and magnetic
fields, respectively. The values
di= dd of the impedance matrix
components obtained at the lower boundary of integration
z=zd are
recalculated to the height
z=h in the vacuum. The formulae for such
recalculation we obtain using the following matrix of the reflection index of
the plane wave
n],
where
Z0 =(m0/e0)1/2, and
Etg and
Htg are the
tangential to the considered surface components of the electric and magnetic
fields, respectively. The values
di= dd of the impedance matrix
components obtained at the lower boundary of integration
z=zd are
recalculated to the height
z=h in the vacuum. The formulae for such
recalculation we obtain using the following matrix of the reflection index of
the plane wave
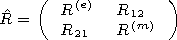

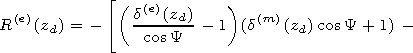
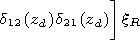

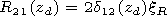
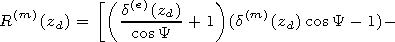
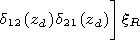
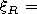

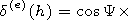
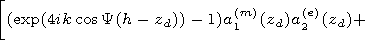



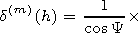
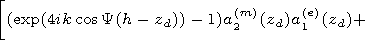
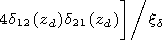
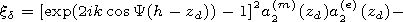
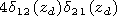
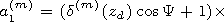
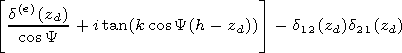

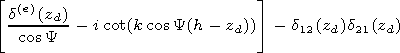
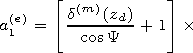
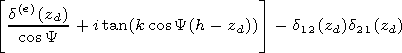
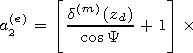
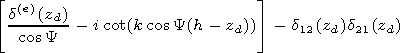
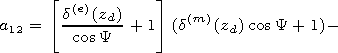
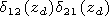
 di/
di/  Y,
is integrated. Also
the formulae of recalculation of the derivative in vacuum were derived and
used. The value of the Earth's surface impedance
dg is determined by the
given values of the relative dielectric permeability and conductivity for the
two-layer model of the underlying surface.
Y,
is integrated. Also
the formulae of recalculation of the derivative in vacuum were derived and
used. The value of the Earth's surface impedance
dg is determined by the
given values of the relative dielectric permeability and conductivity for the
two-layer model of the underlying surface.