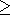 40 AU) in 1995-1996 as compared
with 1987. For
the 130-230 MeV
proton channel, the ratio between intensities in
1996 and 1987 was
J96/J87
40 AU) in 1995-1996 as compared
with 1987. For
the 130-230 MeV
proton channel, the ratio between intensities in
1996 and 1987 was
J96/J87  1.23 at the Earth's orbit,
0.44 at
r
1.23 at the Earth's orbit,
0.44 at
r  42 AU, and as low as 0.29 at
r
42 AU, and as low as 0.29 at
r  64 AU.
64 AU.
M. S. Kalinin and M. B. Krainev
P. N. Lebedev Physical Institute, Moscow, Russia
The data obtained by a network of spacecraft (IMP 8, Pioneer 10,
and Voyager 2)
during more than 2 decades and covering large
spatial scales (up to
r = 65 AU) allow
comparative analysis of the GCR
intensity behavior during two
successive 11-yr solar cycles. In spite of a limited amount of
data, this analysis
[Webber and Lockwood, 1997]
has
revealed a rather unexpected intensity behavior in the distant
heliosphere. If we consider only successive solar minima - the GCR
intensity measured by IMP 8 ( r = 1 AU)
in 1996 was approximately
equal to that in 1976 - an unexpected very weak increase in the
GCR intensity with radial distance is revealed in the distant
heliosphere ( r  40 AU) in 1995-1996 as compared
with 1987. For
the 130-230 MeV
proton channel, the ratio between intensities in
1996 and 1987 was
J96/J87
40 AU) in 1995-1996 as compared
with 1987. For
the 130-230 MeV
proton channel, the ratio between intensities in
1996 and 1987 was
J96/J87  1.23 at the Earth's orbit,
0.44 at
r
1.23 at the Earth's orbit,
0.44 at
r  42 AU, and as low as 0.29 at
r
42 AU, and as low as 0.29 at
r  64 AU.
64 AU.
These data, supplemented by Ulysses data on global latitudinal GCR gradients [Heber et al., 1996] and spectra measured by IMP 8 at the Earth's orbit, have been described by numerical solutions of the transport equation with standard boundary conditions [Potgieter, 1997]. It has been shown that in order to satisfactorily describe the spatial GCR distribution in the heliosphere at two successive intensity maxima (solar minima) periods, the main parameter of the model - radial diffusion coefficient - should be taken to be 5-6 times greater for the intensity maximum in 1987 (when the radial projection of the interplanetary magnetic field in the Northern Hemisphere was negative, A = -1 ) than for the intensity maximum in 1996 (when the projection was positive, A = 1 ). Another characteristic of the spatial distribution - latitudinal intensity gradients at 40-60 AU - proved to be too small for the period with A = -1 in this case.
The goal of this work was to show, based on numerical solution of the transport equation for protons, that experimental data on the radial intensity behavior can be satisfactorily described if we introduce additional modulation beyond the outer heliosphere boundary due to the modulating action of the electrostatic potential that changes its sign at the TSMF polarity reversal.
The spatial distribution of proton intensity was calculated by numerically solving the two-dimensional (with respect to spatial variables r (radial distance) and q (polar angle)) axisymmetric stationary diffusion equation including drift [Toptygin, 1983]
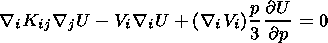 | (1) |
where
U is the particle density in the phase space ( r,p) related to the intensity
J as
J = p2U;
Kij is the total
diffusion tensor (DT) whose nonsymmetric part describing drifts
corresponds to coefficients
KT  KTf(q,a) for
the tilt angle of the current sheet of
a = 5o modified
according to
Potgieter and Moraal [1985]
and
Jokipii and Kota [1989];
and
Vi is the solar wind (SW) velocity having
only radial component depending on both spatial coordinates. The
actual dependence of the SW velocity on coordinates was
qualitatively consistent with the Ulysses data and was approximated
as
KTf(q,a) for
the tilt angle of the current sheet of
a = 5o modified
according to
Potgieter and Moraal [1985]
and
Jokipii and Kota [1989];
and
Vi is the solar wind (SW) velocity having
only radial component depending on both spatial coordinates. The
actual dependence of the SW velocity on coordinates was
qualitatively consistent with the Ulysses data and was approximated
as
 |
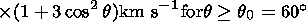 | (2) |
where r0 is the photosphere radius. At q< 60o, the SW velocity was latitude-independent and corresponded to the solution of (2) for q = 60o.
The symmetric part of the DT describing diffusion was taken to be
fully anisotropic; and the components normal to the magnetic field
were assumed to be proportional to the field-aligned component
K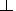 r = a1K
r = a1K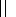 ,
K
,
K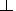 q
= a2K
q
= a2K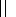 .
Fixed coefficients
a1 and
a2 were chosen so as
to fit the radial intensity behavior and to ensure the ratio
between the intensities at the pole and helioequator for radial
distances
r
.
Fixed coefficients
a1 and
a2 were chosen so as
to fit the radial intensity behavior and to ensure the ratio
between the intensities at the pole and helioequator for radial
distances
r  1 AU limited by 1.4-1.5
[Heber et al., 1996].
The field-aligned diffusion coefficient is given by
1 AU limited by 1.4-1.5
[Heber et al., 1996].
The field-aligned diffusion coefficient is given by
 | (3) |
Here, the dimensional coefficient
K0 measured in terms of
6 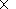 1020 cm2 s-1
was adjusted in calculations;
b = n /c,
where
n is the particle velocity and
c is the speed of light; and
function
f1(R), where
R is rigidity, was chosen so as to fit
experimental data. In practice, a simple dependence
1020 cm2 s-1
was adjusted in calculations;
b = n /c,
where
n is the particle velocity and
c is the speed of light; and
function
f1(R), where
R is rigidity, was chosen so as to fit
experimental data. In practice, a simple dependence
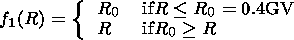 | (4) |
was used.
The antisymmetric coefficient
KT describing drift was taken in the
standard form
KT = K0(a) 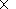 f(q, a)
f(q, a)
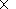 b
b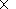 R/3B, where
B is the value of the interplanetary magnetic
field (IMF); and coefficient
K0(a),
typically equal to unity,
was varied to control the effect of drift. Function
f2(r) = 1 +rn,
where
r is expressed in AU.
R/3B, where
B is the value of the interplanetary magnetic
field (IMF); and coefficient
K0(a),
typically equal to unity,
was varied to control the effect of drift. Function
f2(r) = 1 +rn,
where
r is expressed in AU.
Equation (1) was solved with the standard initial condition U( r,pm) = UH(pm), where UH(p) is the unmodulated particle density in the Galaxy, pm = 100 GeV s-1, and conditions at the outer boundary r = rM of the modulation region are U(rM, q, p) =UH(p).
The effect of external modulation beyond the modulation region was provided by the modulating action of the electrostatic potential (EP), which was described by the expressions obtained earlier by Kalinin and Krainev [1992, 1997] (see also Krainev [1979] and Jokipii and Levy [1979]), but shifted by the value a which was chosen so as to fit experimental data
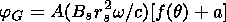 | (5) |
where
A = 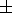 1 indicates the TSMF polarity,
rs is the radius of
the magnetic field source surface,
w is the angular speed of
rotation of the Sun,
Bs is the radial component of the magnetic
field at the source surface, and function
f(q) describes the
latitudinal dependence according to
Kalinin and Krainev [1992].
In calculations, coefficient
(Br02w/c)
equal to 0.25 GV,
typical of the heliosphere was used. The particle
density was recalculated for the outer boundary of the modulation
region by using the relation
U(rM, q, p)
= UH(p + Dp),
where
rM = 100 AU
is the modulation region radius (Liouville
theorem). In this expression,
p and
p' = p + Dp are
related by the energy integral
1 indicates the TSMF polarity,
rs is the radius of
the magnetic field source surface,
w is the angular speed of
rotation of the Sun,
Bs is the radial component of the magnetic
field at the source surface, and function
f(q) describes the
latitudinal dependence according to
Kalinin and Krainev [1992].
In calculations, coefficient
(Br02w/c)
equal to 0.25 GV,
typical of the heliosphere was used. The particle
density was recalculated for the outer boundary of the modulation
region by using the relation
U(rM, q, p)
= UH(p + Dp),
where
rM = 100 AU
is the modulation region radius (Liouville
theorem). In this expression,
p and
p' = p + Dp are
related by the energy integral
 | (6) |
Here, q is the particle charge.
As a result, a radial intensity profile of the 200-MeV protons at the helioequator was obtained and then compared with the data of the 130-230 MeV proton channel at the spacecraft obtained by Webber and Lockwood [1997].

|
| Figure 1 |
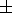 1. Figure 1b
presents calculated spectra in comparison
with the spectra obtained by IMP 8
for the same time periods. UMS
denotes the unmodulated spectrum at the modulation region boundary.
1. Figure 1b
presents calculated spectra in comparison
with the spectra obtained by IMP 8
for the same time periods. UMS
denotes the unmodulated spectrum at the modulation region boundary.
It is clear from the magnitudes of the parameters given in
the caption
to Figure 1
that even in the case of a two-fold decrease in drift
effects, coefficient
K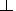 r,
responsible for radial gradients
in the distant heliosphere, must be chosen low enough to provide the
required large intensity drop within the interval of distances
r,
responsible for radial gradients
in the distant heliosphere, must be chosen low enough to provide the
required large intensity drop within the interval of distances
 20 AU
from the outer boundary of the modulation region.
20 AU
from the outer boundary of the modulation region.

|
| Figure 2 |
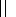 should be
sufficiently high to provide these small radial gradients. The
relevant latitudinal dependence of intensity for
A = 1 and
r = 1 AU
is shown in Figure 2.
To provide the required latitudinal gradient,
the coefficient
K
should be
sufficiently high to provide these small radial gradients. The
relevant latitudinal dependence of intensity for
A = 1 and
r = 1 AU
is shown in Figure 2.
To provide the required latitudinal gradient,
the coefficient
K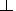 q
should exceed
K
q
should exceed
K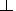 r approximately by
a factor of 10.
r approximately by
a factor of 10.

|
| Figure 3 |
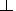 r) by a factor of
5-6. In this case, realistic latitudinal
gradients for radial distances of ~1 AU result. Calculations and
also initial parameters are shown in Figure 3.
It is evident that
in this case, the situation at
A = 1 is not described.
r) by a factor of
5-6. In this case, realistic latitudinal
gradients for radial distances of ~1 AU result. Calculations and
also initial parameters are shown in Figure 3.
It is evident that
in this case, the situation at
A = 1 is not described.
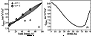
|
| Figure 4 |
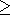 20 AU
corresponds to the intensity at the
helioequator). It is obvious that the negative latitudinal gradient
changes the sign at distances
20 AU
corresponds to the intensity at the
helioequator). It is obvious that the negative latitudinal gradient
changes the sign at distances
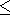 20 AU.
However, as shown in the
right-hand panel (b) presenting latitudinal intensity dependence
for
A = -1 at radial distance
20 AU.
However, as shown in the
right-hand panel (b) presenting latitudinal intensity dependence
for
A = -1 at radial distance
 64 AU, this maximum
latitudinal gradient does not exceed 1%/AU. It is by a factor of
2-3 lower than the experimental estimates given by
Webber and Lockwood [1997]
for
r = 42 AU and extrapolated to
r = 64 AU.
64 AU, this maximum
latitudinal gradient does not exceed 1%/AU. It is by a factor of
2-3 lower than the experimental estimates given by
Webber and Lockwood [1997]
for
r = 42 AU and extrapolated to
r = 64 AU.
The major conclusion inferred from the above consideration is that the transport equation is not able to describe the experimental spatial GCR distribution within the heliosphere at successive solar minima periods in terms of the standard approach involving the same set of kinetic coefficients. To adequately describe measurements, at least the diffusion coefficients responsible for the radial distribution of the GCR intensities must considerably differ in these sets (by a factor of 5-6).
Thus, the obtained results confirm the conclusions made by
Potgieter [1997],
who considered an analogous problem in terms of
another model dependence of the diffusion coefficients on the
rigidity. Note also that our results are not the consequence of the
diffusion coefficient dependence on the radial distance in the form
K
 (1+r) that
we have chosen. For instance, the
K
(1+r) that
we have chosen. For instance, the
K
 1/B dependence (where
B is the IMF value) often
used gives the same qualitative picture. The difference is in
insignificant changes in the transport equation parameters.
1/B dependence (where
B is the IMF value) often
used gives the same qualitative picture. The difference is in
insignificant changes in the transport equation parameters.
The results given in the previous section suggest that other modulating factors can exist. By considering them, it is possible to avoid inconsistencies arising in description of the measured spatial GCR distribution. It is quite natural that these factors must be associated with the Sun - the only cause and source of modulation - and, in addition, they must exhibit a "correct" dependence on the sign of the 22-yr solar cycle phase (that is, on the sign of A ) and on heliolatitude. In a correct dependence, the effects of these factors fit the experimentally observed GCR behavior.
If we extend the radial intensity dependence to the outer
heliosphere boundary using the same gradients as in the distant
heliosphere, it becomes evident that two successive solar minima
can have different intensity levels at the outer heliosphere
boundary. In this case, the ratio between unmodulated intensities
for the energy interval considered must be
 3-4. However,
the attempt to describe the radial intensity behavior at two
successive solar minima by varying only the value of the intensity
spectrum at the modulation region boundary, without changing its
shape (that is, with unvaried energy dependence), and by using the
same set of transport equation coefficients for different signs of
A is not justified, on the one hand, and does not give the desired
result, on the other hand.
3-4. However,
the attempt to describe the radial intensity behavior at two
successive solar minima by varying only the value of the intensity
spectrum at the modulation region boundary, without changing its
shape (that is, with unvaried energy dependence), and by using the
same set of transport equation coefficients for different signs of
A is not justified, on the one hand, and does not give the desired
result, on the other hand.
Kalinin and Krainev [1992, 1997] derived the expression for the heliospheric electrostatic potential (EP) averaged over the azimuthal variable relative to infinity on the basis of the Parker spiral IMF structure and high electric conductivity of the SW plasma. Since the EP induced in this heliosphere model is completely included in the transport equation, which is solved for the inner regions of the heliosphere, the action of such induction field beyond the heliosphere can be reduced, in the first approximation, to the effect of its EP on the intensity spectrum at the heliosphere boundary. In this case, the dependence of EP on global sign-defining multiplier A describing polarity of the 11-yr cycle and on latitude provides the necessary and correct dependence on it of the modulating effect beyond the heliosphere. The EP value necessary to provide the required modulation level at the modulation region boundary for different A is determined by the intensity difference in the distant heliosphere. It depends also on how completely physical mechanisms affecting the true unmodulated intensity spectrum at large distances beyond the heliosphere are taken into account. If we ignore energy losses of particles during their travel to the outer heliosphere boundary from the local interstellar medium and assume the efficient action of nondissipative scattering, the particle density along their trajectories in the phase space must be preserved, according to the Liouville theorem. If, in determining the phase trajectories, we restrict ourselves to the EP effect and ignore the IMF influence, all trajectories will belong to the constant-energy surfaces with uniform filling. In this case, the spectrum at the modulation region boundary can be found from the expression: U( rM, p) = UH(p') (see the expression in the above discussion). Note that this approach can be regarded only as the first approximation to the actual picture, but it is useful owing to its simplicity [Jokipii and Levy, 1979].
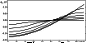
The qualitative picture of the modulating EP effect beyond the heliosphere in terms of the approach described above is sufficiently clear and follows from (6). It is not reduced to a mere change in the spectral amplitude at the heliosphere boundary. For the period with A = -1, the EP effect at low latitudes leads to a considerable shift of the initial unmodulated intensity spectrum toward higher kinetic energies (that is, the spectrum goes higher and simultaneously is cut from the left).

|
| Figure 5 |
Thus, the intensity spectrum at the heliosphere boundary for any above-threshold energy determined by the EP amplitude (~125 MeV) at A = 1 is lower in near-equatorial regions and higher in the polar regions as compared with that at A = -1, thereby providing the necessary sign of the effect. In addition, this picture of the influence on the unmodulated intensity spectrum should lead to increasing latitudinal gradient in the distant heliosphere, thus providing a better fit to measurements.
|
| Figure 6 |

|
| Figure 7 |
 0.125 GeV,
the latitudinal dependence
remaining the same. The qualitative picture of the EP effect on the
radial intensity behavior for different
A and relevant transport
equation coefficients (given under Figures 2 and 3) providing
adequate description of the radial behavior without the EP effect
is presented in Figure 7.
The lower curve in panel (a) and the
upper curve in panel (b) correspond to
a = 0.5. Figure 7
demonstrates a higher sensitivity of intensity to the EP value in
the distant heliosphere at
A = -1.
The intensity at distances
0.125 GeV,
the latitudinal dependence
remaining the same. The qualitative picture of the EP effect on the
radial intensity behavior for different
A and relevant transport
equation coefficients (given under Figures 2 and 3) providing
adequate description of the radial behavior without the EP effect
is presented in Figure 7.
The lower curve in panel (a) and the
upper curve in panel (b) correspond to
a = 0.5. Figure 7
demonstrates a higher sensitivity of intensity to the EP value in
the distant heliosphere at
A = -1.
The intensity at distances
 20 AU from the boundary drops more than
by an order of
magnitude.
This is associated with a characteristic peak-like shape
of the intensity spectrum in the region of energies approximately
equal to the amplitude of
jG at
A = -1. With this
A, the EP
effect on the intensity for
a = 0 (the lower curve in panel (b)) is
insignificant for radial distances 1-64 AU.
On the contrary, at
A= 1,
the effect of the potential is more pronounced in the middle
and near heliosphere because at positive
A, the mechanism of
particle drift from near-polar regions of the heliosphere toward
the equator is efficient.
20 AU from the boundary drops more than
by an order of
magnitude.
This is associated with a characteristic peak-like shape
of the intensity spectrum in the region of energies approximately
equal to the amplitude of
jG at
A = -1. With this
A, the EP
effect on the intensity for
a = 0 (the lower curve in panel (b)) is
insignificant for radial distances 1-64 AU.
On the contrary, at
A= 1,
the effect of the potential is more pronounced in the middle
and near heliosphere because at positive
A, the mechanism of
particle drift from near-polar regions of the heliosphere toward
the equator is efficient.

|
| Figure 8 |
 40 AU
go higher than
the experimental points. An intensity decrease can be achieved only
by limiting the linear growth of the diffusion coefficient with
1 +r by the values corresponding to some radial distance
rP. A
reasonable result given in Figure 8 (panel (b)) can be obtained for
rP = 50 AU. Figure 8 shows that the radial intensity behavior
at
A= -1 is more sensitive to the EP value than at
A = 1. In addition,
the intensity at
A = -1 in the distant heliosphere remains somewhat
higher than the experimental values. Since the point at
r = 64 AU
was obtained by extrapolating the intensity at 42 AU (see above),
and measurements for
r
40 AU
go higher than
the experimental points. An intensity decrease can be achieved only
by limiting the linear growth of the diffusion coefficient with
1 +r by the values corresponding to some radial distance
rP. A
reasonable result given in Figure 8 (panel (b)) can be obtained for
rP = 50 AU. Figure 8 shows that the radial intensity behavior
at
A= -1 is more sensitive to the EP value than at
A = 1. In addition,
the intensity at
A = -1 in the distant heliosphere remains somewhat
higher than the experimental values. Since the point at
r = 64 AU
was obtained by extrapolating the intensity at 42 AU (see above),
and measurements for
r 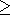 64 AU
are not available, this
difference cannot be considered significant.
64 AU
are not available, this
difference cannot be considered significant.
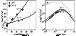
|
| Figure 9 |
 20 AU
near the outer boundary. The
calculations and the values of coefficients used are shown in
Figure 9a.
Panel b of Figure 9
presents the calculated spectra for
r = 1 AU.
20 AU
near the outer boundary. The
calculations and the values of coefficients used are shown in
Figure 9a.
Panel b of Figure 9
presents the calculated spectra for
r = 1 AU.
The obtained results show that
1. It is impossible to fit the measurements of spatial GCR distribution in the heliosphere at successive solar minima in terms of the standard approach to the solution of the transport equation involving the use of the same set of diffusion coefficients. There is a question: whether the difference in transport equation parameters corresponds to the difference in actual physical conditions of the GCR particle propagation in the heliosphere at successive solar minima periods is distinguished, according to modern ideas, only by the TSMF sign. The question still remains unresolved.
2. Since the required difference in diffusion coefficients is associated with a low intensity level in the distant heliosphere at the solar minimum when the TSMF sign was positive and the drift mechanism had to be effective, the question about the actual contribution of drifts into modulation arises. The contribution of drifts derived from the standard first-order orbit theory is likely to be overestimated, and the fit to measurements can be achieved only by assuming the contribution of this mechanism to be half its standard value. Since a much lower radial diffusion coefficient in the distant heliosphere is also required to fit measurements during this period, this result can be interpreted as the effect of diffusion on the drift efficiency (a low diffusion coefficient corresponding to intense scattering leads to a weaker drift mechanism).
3. One of the ways to avoid inconsistencies accompanying the
standard approach is to assume that the radius of the Sun's action
on charged GCR particles extends beyond the boundaries of the
modulation region, which is typically thought of as heliosphere
sizes. A direct physical mechanism in this case is the EP effect on
the GCR intensity spectrum beyond the modulation region. According
to the results given in section 3,
the EP having the amplitude of
250-300 MV and depending on the TSMF sign is needed to fit
measurements. This potential differs from the EP typically
associated with the heliosphere by a shift by a constant value,
Br02w/2c
 125 MV;
the latitudinal dependence
remains unvaried. This EP value can be associated with the
positively charged heliosphere when the total charge within any
radius is not zero. This possibility cannot be excluded, though
there are no arguments in favor of this hypothesis as well. Another
possible way to increase the EP amplitude can be taken into
account: the latitudinal dependence of the magnetic field at the
source surface, which is usually neglected for simplicity
[Krainev, 1981].
Consideration of both assumptions is beyond the
scope of this paper. In conclusion, a conceptually similar
approach, but in terms of a more realistic model, was successfully
employed by
Jokipii and Kota [1997]
to describe the radial
behavior of the anomalous CR component.
125 MV;
the latitudinal dependence
remains unvaried. This EP value can be associated with the
positively charged heliosphere when the total charge within any
radius is not zero. This possibility cannot be excluded, though
there are no arguments in favor of this hypothesis as well. Another
possible way to increase the EP amplitude can be taken into
account: the latitudinal dependence of the magnetic field at the
source surface, which is usually neglected for simplicity
[Krainev, 1981].
Consideration of both assumptions is beyond the
scope of this paper. In conclusion, a conceptually similar
approach, but in terms of a more realistic model, was successfully
employed by
Jokipii and Kota [1997]
to describe the radial
behavior of the anomalous CR component.
Heber, B., et al., Spatial variation of > 40 MeV/n nuclei fluxes observed during the Ulysses rapid latitude scan, Astron. Astrophys., 316, 538, 1996.
Jokipii, J. R., and J. Kota, The polar heliospheric magnetic field, Geophys. Res. Lett., 16 (1), 1, 1989.
Jokipii, J. R., and J. Kota, The energy spectrum of anomalous cosmic rays, in Proceedings of the 25th International Cosmic Ray Conference, vol. 2, pp. 229-232, Durban, 1997.
Jokipii, J. R., and E. H. Levy, Electric field effects on galactic cosmic rays at the heliospheric boundary, in Proceedings of the 16th International Cosmic Ray Conference, vol. 3, pp. 52-56, Kyoto, Japan, 1979.
Kalinin, M. S., and M. B. Krainev, The electromagnetic heliospheric field and galactic cosmic rays during the periods of low solar activity, in Mathematical Models of the Near Space, Proceedings of the 2nd National Meeting in Memory of V. P. Shabanskiy (in Russian), Moscow University, Moscow, 1992.
Kalinin, M. S., and M. B. Krainev, The electric field beyond the termination shock and some possible GCR and ACR effects, Adv. Space Res., 19 (6), 969, 1997.
Krainev, M. B., The solar corona expansion geometry and cosmic ray effects, IV, On the cosmic ray energy change due to the electric field, in Proceedings of the 16th International Cosmic Ray Conference, vol. 3, pp. 236-241, Kyoto, Japan, 1979.
Krainev, M. B., The electromagnetic field in and outside the solar wind cavity and the galactic cosmic rays, in Proceedings of the 17th International Cosmic Ray Conference, vol. 3, p. 357, Paris, 1981.
Potgieter, M. S., Applications of enhanced perpendicular diffusion in the heliospheric modulation of cosmic rays, in Proceedings of the 25th International Cosmic Ray Conference, vol. 2, pp. 1-4, 1997.
Potgieter, M. S., and H. Moraal, A drift model for the modulation of galactic cosmic rays, Astrophys. J., 294 (2), 425, 1985.
Toptygin, I. N., Cosmic Rays in the Interplanetary Magnetic Fields (in Russian), Nauka, Moscow, 1983.
Webber, W. R., and J. A. Lockwood, Intensities of anomalous and galactic cosmic rays in the outer heliosphere near the heliospheric equator in 1987 and during the period from 1994 to 1996, J. Geophys. Res., 102, 9773, 1997.