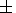 0.06, on average.
0.06, on average.
B. I. Klain and N. A. Kurazhkovskaya
Borok Geophysical Observatory, Yaroslavl Region, Russia
Studies of geomagnetic storms play an essential role in analyzing of the solar wind plasma interaction with the Earth's magnetosphere. It is known since the work of Akasofu and Chapman [1975] that geomagnetic storms are one of the solar activity manifestations which results in a global depletion of the magnetic field H component. A typical scheme of the magnetic storm development includes several phases. The arriving to the Earth of the high-velocity plasma and related shock wave leads to a sharp increase in the H component which constitutes a storm sudden commencement (SSC) [Nishida, 1980]. SSC is followed by a short period during which the magnetic field does not show any considerable changes, the fact being manifested by the positive values of the Dst index. This stage of the geomagnetic storm development is caused by the additional compressing of the magnetosphere by the increased pressure of the solar wind and is called the initial phase. The initial phase is determined as a quiet state of the magnetic field which may last for several hours. However, in the magnetosphere at high latitudes in the midday sector of the sunlit hemisphere, an intensification of wave processes after a sudden commencement is observed [Akasofu and Chapman, 1975].
Numerous studies have shown that the influence of geomagnetic storms is significant on the wave field dynamics of the region of dayside cusp and polar cap where various oscillatory regimes are observed [Nishida, 1980]. The long period irregular geomagnetic pulsations with periods from 3 to 20 min belong to one of the most characteristic oscillatory regimes in the region of dayside cusp and polar cap. They are called as ipcl-type (irregular pulsations, continuous, long) [Bolshakova et al., 1975]. The pulsations ipcl have maximum intensity in the regions of the cusp. The amplitude of these pulsations depends on the solar wind velocity and negative values of IMF Bz [Troitskaya and Bolshakova, 1988]. It was shown by Kleimenova et al. [1985] that there are at least two different types of ipcl pulsations in two frequency bands: 2.1-5.6 mHz (3-8-min period), "noise pulsations" (np), and 0.8-1.1 mHz (15-20-min period), "long period" (lp). In this paper we investigate the np pulsations, which look like the permanent stationary noise in the 3-8 min range. The pulsations np have the following properties [Kleimenova et al., 1985]: (1) they have maximum intensity at a very narrow geomagnetic latitude region (74o- 76o during weak and moderate geomagnetic activity ( Kp index ~1-3); (2) the maximum of their occurrence falls on the prenoon time (0600-1100 MLT); (3) the average amplitudes of np pulsations are about 40-60 nT; and (4) np pulsations occur at both IMF Bz<0 and Bz>0.
It is believed that the geomagnetic pulsation characteristics manifest the processes of the solar wind interaction with the terrestrial magnetosphere during geomagnetic storms.
Earlier, Kurazhkovskaya and Klain [1995] studied the dynamics of the np-pulsation amplitude during severe magnetic storms. We have found that the highest intensity of the np pulsations is observed in the beginning of the main phase of a storm. However, an intensification of the np pulsations begins yet during the initial phase of a storm. Therefore, not only the amplitude but the spectral composition and field structure of geomagnetic pulsations are changed dramatically.
It should be noted that irregular np pulsations are a chaotic
signal very difficult to study, especially in disturbed conditions.
Recently, the fractal analysis methods began to be used to study
such vibrational processes
[Burlaga and Klein, 1986;
Mundt et al., 1991;
Vassiliadis et al., 1990;
Voros, 1991].
Klain and Kurazhkovskaya [1998, 1999,
2000a, 2000b]
were the first to use the
fractal approach to the analysis of the nature of long-period
irregular pulsations. They
showed that the ipcl burst
regime and "noise" pulsations have a fractal structure.
The fractal dimensionality for 30 series of
ipcl pulsations are computed to be
1.83 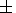 0.06, on average.
0.06, on average.
As a result of the studies performed, the fractal characteristics of long-period irregular pulsations have been obtained, and their relations to the interplanetary medium parameters and structural formations in the magnetosphere have been revealed. For example, Klain and Kurazhkovskaya [1998] showed that the fractal dimensionality dynamics of series of ipcl pulsation bursts and, respectively, variations of the oscillations structure, are controlled by the magnitude of the interplanetary magnetic field (IMF) B. Certain threshold value of B was obtained. When this value is exceeded, the burst structures are destroyed the chaos degree of the vibrations increases and the burst ipcl regime is transformed into a homogeneous stationary noise.
Studies of the np-pulsation fractal properties at the meridional
chain of observatories showed that the np-pulsation field
structure depends on the geomagnetic latitude.
For moderate perturbed
condition the latitudinal profile of fractal dimensionality
np-pulsations was constructed. It was revealed, that in a
narrow interval of latitude (69o-
71o the value of
D is less
( D 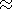 1.62 ), than at lower and high
latitudes
( D
1.62 ), than at lower and high
latitudes
( D 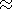 1.78-1.82 ).
It was made it possible
to obtain information on the magnetospheric resonator boundary
under moderate geomagnetic activity
[Klain and Kurazhkovskaya, 1999,
2000a].
1.78-1.82 ).
It was made it possible
to obtain information on the magnetospheric resonator boundary
under moderate geomagnetic activity
[Klain and Kurazhkovskaya, 1999,
2000a].
The fractal analysis of np pulsations performed by Klain and Kurazhkovskaya [2000b], showed that there exists an asymmetry of the dynamics of the fractal dimensionality of the np pulsations observed simultaneously in the conjugated points of the magnetosphere. The analyzed events have been divided into two groups depending on the value of the np pulsation fractal dimensionality in the Northern and Southern Hemispheres of the magnetosphere: D N/D S > 1 (group I) and D N/D S < 1 (group II) [Klain and Kurazhkovskaya, 2001]. It has been found that the probability of observation of the group I and group II events depends on the IMF orientation and direction of the azimuthal component of the solar wind electric field ( Ey ). Events of the group I are observed at Bz < 0 and Ey >0. Events of the group II are observed at Bz > 0 and Ey <0. Comparing the fractal dimensionality of the np pulsations in both hemispheres, the influence of the turbulent level of the stationary field-aligned currents entering the ionosphere in the prenoon sector of the magnetosphere in the vicinity of the auroral oval on the pulsation chaosization was found.
Studies of the fractal properties of long-period irregular pulsations during geomagnetic storms was left outside our consideration. This paper continues, on one hand, our studies of morphological characteristics of the np pulsations during magnetic storms [Kurazhkovskaya and Klain, 1995], and, on the other hand, studies of the fractal properties of these pulsations [Klain and Kurazhkovskaya, 1998, 1999, 2000a, 2000b] and their relations to various geophysical events. Since the dynamics of the np-pulsation fractal characteristics may be specific at various phases of a geomagnetic storm, for the beginning we analyze it at the initial phase of a storm.
This paper is aimed at studying of the dynamics of the np-pulsation fractal dimensionality during the initial phase of a geomagnetic storm, as well as to investigate the np-pulsation relation to the main characteristics of this phase of a storm.
The data used in this study are continuous recordings of the magnetic field variations at the Antarctic magnetic observatory Mirny (geographic coordinates 66.6o S, 93.0o E; corrected geomagnetic coordinates -77.2, 122.7) for 1981-1986 (rapid-run magnetograms, 90 mm h -1 ), archived at the Geophysical Observatory Borok). These magnetograms were digitized with a resolution of 10 s for the periods of selected magnetic storms. The time series obtained were approximated by the least square method using the Chebyshev polynomial [Korn and Korn, 1968]. Then the trend was withdrawn by subtracting the smoothed signal from the initial realizations. Fourteen storms were chosen, fulfilling the following criteria: (1) all the storms were of the burst type with a sudden commencement; (2) the SSC was observed, as a rule, during the daytime, when the Mirny observatory was located in the noon sector of the sunlit hemisphere; (3) all the storms were isolated, that is, they contained no recovery phases of a preceding storm ( Dst > 0 in the initial phase of a storm); (4) all the storms were moderate or strong according to the classification by Loewe and Proells [1997] and the value of the Dst variation during the main phase was from -50 to -200 nT; (5) the duration of the storm initial phase was longer than 1 hour.
Table 1 lists storms chosen to analyze the np-pulsation fractal dimensionality. The date of the storm beginning, SSC moment, minimum value of the Dst variation during the main phase of the storm and the time interval of the np pulsations analyzed are presented in Table 1.
First, we analyzed the records of np pulsations during the initial phase of each storm. The spectral densities of the np pulsations were obtained by the fast fourier transformation [Otnes and Enochson, 1982]. The maximum of the analyzed np-pulsation signals is identified to be in the 2.1-5.5 mHz frequency range. Analyzing the obtained spectra, we found that the pulsation spectral density at low frequencies changes according to the power law
 |
where f is a frequency, a is a power index, and S is a spectral density. Since the spectral density of the np pulsations is a power function, the analyzed signals may be considered as fractal formations with the dimensionality ( D ) [Feder, 1991], and the power index a may be used to calculate D [Berry, 1979]. To determine the spectral density index a, we used the "critical exponents" method proposed by Nakagawa [1993] and based on calculations of the signal power spectra momenta. We omit here a detailed description of the method, noting only that it is based on calculations of the functions of the type
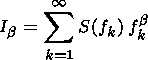 | (1) |
where b is a power index. Further an asymptotic in terms of the b function is used:
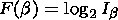 | (2) |
which makes it possible to determine the critical value bc. The value of bc is related to a by the expression
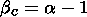 | (3) |
According to Berry [1979] one can find the fractal dimensionality from the relation
 | (4) |
Thus, using equation (2) and (3) one can find bc and a, respectively. Then, using equation (4), one can find the signal fractal dimensionality D. This method is most usable for time series the power spectra of which at low frequencies is a typical power function. The critical exponent method is simple, convenient to use, and has already been used, for example, by Klain and Kurazhkovskaya [1998]. Using the critical exponent method, one can obtain D within the needed accuracy. In our calculations, the error of the fractal dimensionality of every pulsation time series.

|
| Figure 1 |
Figure 1 shows that the np-pulsation regime has a noise character and its spectral density at lower frequencies is fairly well approximated by a power function. The crossing point of the tangent to function (2) projected onto the b axis gives the value of bc which in this case is 0.22. It follows from equation (3) that a=1.22 and thus the np-pulsation fractal dimensionality is 1.89.
Using the procedure of determination of time series fractal structure described above, the value of D for all the pulsation observation intervals analyzed in this paper was determined. The analysis showed that the D value is different for different events. Before describing the results obtained, we make an essential note which clarify the sense of the fractal dimensionality.
According to
Feder [1991]
the fractal dimensionality is related to
the Herst power index
H by the formula:
D = 2 - H. It is known that
there exist three intervals for classification of the Herst index:
(1)
H = 0.5, (2)
0 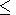 H < 0.5, and (3)
0.5 < H < 1.0.
The first value
corresponds to random series (the Brownian motion). The second and
third ranges of the Herst index correspond to antipersistent and
persistent (generalized Brownian motion) series, respectively. It
should be noted that when the
H value increases ( D decreases) the
time series become more structured. However, a decrease of
H (increase of
D ) means that the series are more noisy. Thus,
D is an
indicator of the changes in the structure of time series and a
qualitative measure of these changes. In other words, the fractal
dimensionality characterize the chaotic degree of the oscillation
process.
H < 0.5, and (3)
0.5 < H < 1.0.
The first value
corresponds to random series (the Brownian motion). The second and
third ranges of the Herst index correspond to antipersistent and
persistent (generalized Brownian motion) series, respectively. It
should be noted that when the
H value increases ( D decreases) the
time series become more structured. However, a decrease of
H (increase of
D ) means that the series are more noisy. Thus,
D is an
indicator of the changes in the structure of time series and a
qualitative measure of these changes. In other words, the fractal
dimensionality characterize the chaotic degree of the oscillation
process.
The fractal dimensionality of np pulsations is close to 2. This
means that the time series of the signals analyzed are very
changeable and chaotic. According to this value of
D, the Herst
index range
0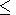 H < 0.5 corresponds to the np-pulsation
regime.
Therefore, the time series are antipersistent or ergodic.
H < 0.5 corresponds to the np-pulsation
regime.
Therefore, the time series are antipersistent or ergodic.
It follows from the D -value analysis that the structures of the np-pulsation field in the initial phase of a storm are different for different events. It is worth clarifying how the fractal dimensionality of irregular pulsations is related to the main characteristics of the storm initial phase: its duration ( Dt ) and Dst -variation value. To do this, a correlation analysis between D and characteristics of the storm initial phase was performed. Before coming to the obtained results, it is worth noting that both Dt and Dst variation are internal parameters of the magnetosphere and manifest the impact of the solar wind plasma flux on the terrestrial magnetosphere in the beginning of the storm. Below we consider the relation of these characteristics to D and, respectively, to the changes of the np-pulsation regime.
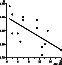
|
| Figure 2 |
The regression formula

|
| Figure 3 |
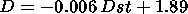 |
describes the relation between D and Dst. The values of the correlation coefficient between D and Dst is -0.65. This experimental fact may be interpreted as an argument in favor of the relations between the np-pulsation fractal dimensionality and Dst variations at the initial phase of a storm. Now we consider the relation between the np-pulsation fractal dimensionality and the duration of the initial phase of a storm ( Dt ). Figure 3 shows the dependence of D on Dt for the storms analyzed. The duration of the initial phase is determined as the time interval between the storm sudden commencement (SSC) moment and the beginning of the decrease of the Dst index (that is, the main phase of the storm).
It follows from Figure 3
that there exists an inverse correlation between
D and
Dt.
The longer is the duration of a magnetic storm, the lower is the
value of the np-pulsation fractal dimensionality corresponding to
the period of this phase. The relation between
D and
Dt was
found statistically significant ( r 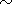 -0.73 ) with the following
regression equation:
-0.73 ) with the following
regression equation:
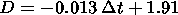 |
Thus, the np-pulsation fractal dimensionality during the initial phase of a storm is related to the Dst index value and the initial phase duration, both parameters manifesting the processes in the magnetosphere occurring in the initial phase period of every geomagnetic storm.
According to Akasofu and Chapman [1975], the Dst variation is a combination of the fields of the currents flowing on the magnetopause (disturbance of corpuscular flux, DCF) and the ring current in the magnetosphere (disturbance of the ring current, DR):
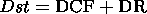 |
Later on, Dremukhina et al. [1999] discussed the contribution to Dst variation of different magnetospheric current systems, including magnetopause current, symmetric ring current, and geotail current. Because of the increase of the solar wind dynamical pressure on the geomagnetic field and compressing of the magnetosphere front boundary, at initial phase of a geomagnetic storm the DCF fields intensify at the magnetopause providing the main input into the Dst variation, whereas the role of the DR currents and of the tail currents is negligible small. Using the np-pulsation fractal analysis, we showed that the variations of the irregular pulsation field structure is evidently governed by two factors: the Dst index and duration of the initial phase of a storm. On the basis of the D dependence on the initial phase duration (Figure 3) one may assume that the structural changes in the np-pulsation regime depend on the characteristic time of the DCF fields action. During storms with short initial phase the np pulsations with relatively high value of the fractal dimensionality are observed and correspondingly represent more chaotic regime. At the same time, a more regular np-pulsation regime is typical for the storms with a durable initial phase.
It follows from Figure 2 that more chaotic np pulsations are observed during the initial phase of a storm under relatively small positive Dst index than under high values of Dst . It has already been mentioned above that during the initial phase, the positive values of Dst index actually are determined by the intensity of the DCF-currents field. Therefore, one can conclude that the storms with more intense current at the magnetopause in the initial phase provide generation of more regular pulsation regimes. It follows from Figures 2 and 3 that most chaotic pulsation regime would be observed during the initial phase of such storms, which either have a short initial phase or small values of the positive values of the Dst variations during this phase.
Thus, the dependencies obtained between D and Dt and also between D and Dst may be interpreted as a manifestation of the influence on the np-pulsation signal structure of the duration of the DCF-currents action at the magnetopause and their intensity in the initial phase of a storm. The relation between the fractal dimensionality of the high-latitude irregular pulsations and the
At the same time, the fractal dimensionality may serve as a measure of the magnetosphere disturbance since this dimensionality is linearly related to the Dst -index value which in its turn characterizes the geomagnetic activity level. Actually (see Figure 2), when the Dst variation is close to zero, the np pulsations have the highest value. Evidently, during the transition of the Dst variations to negative values one should expect even stronger increase of the D value. Transformation of the signal to a homogeneous noise in its turn manifests an increase of the magnetospheric disturbance. Theretofore, the higher is the fractal dimensionality of the np pulsations the more disturbed is the magnetosphere.
1. On the basis of the spectral analysis and "critical exponent" method, the fractal dimensionality of the long-period irregular np-pulsations at the initial phase of 14 geomagnetic storms is determined.
2. A linear dependence of D on positive values of the Dst variations and the duration of the storm initial phase is found. Regression equations relating these values are derived.
3. It is suggested that the structure of the np-pulsation field is governed by the intensity and action time of the DCF fields at the initial phase of a storm.
4. It is proposed to consider the np-pulsation fractal dimensionality as an indicator of the magnetosphere disturbance degree during geomagnetic storms.
Akasofu, S. I., and S. Chapman, Solar-Terrestrial Physics, 512 pp., Oxford Univ., Oxford, 1972.
Berry, M. V., Diffractals, J. Phys. A Meth. Gen., 12, 781, 1979.
Bolshakova, O. V., V. A. Troitskaya, and V. P. Hessler, Determination of position of the polar boundary of the day side cusp from the intensity of high-latitude pulsations, Geomagn. Aeron. (in Russian), 15, 569, 1975.
Burlaga, L. F., and L. W. Klein, Fractal structure of the interplanetary magnetic field, J. Geophys. Res., 91, 347, 1986.
Dremukhina, L. A., Y. I. Feldstein, I. I. Alexeev, V. V. Kalegaev, and M. E. Greenspan, Structure of the magnetospheric magnetic field during magnetic storms, J. Geophys. Res., 104, 28,351, 1999.
Feder, J., Fractals (in Russian), Mir, Moscow, 1991.
Klain, B. I., and N. A. Kurazhkovskaya, Fractal properties of series of bursts of the high-latitude long-period irregular ipcl pulsations, Geomagn. Aeron. (Engl. Transl.), 38 (3), 387, 1998.
Klain, B. I., and N. A. Kurazhkovskaya, Fractal dynamics of the high-latitude long-period irregular pulsations in the frequency band 2.1-5.5 mHz, IUGG XXII General Assembly, Birmingham, UK, July 19-30, 1999, Abstracts B351, 1999.
Klain, B. I., and N. A. Kurazhkovskaya, The dynamics of the fractal dimension of the long-period irregular np pulsations at the meridional network of observatories, Geomagn. Aeron. (Engl. Transl.), 40 (4), 511, 2000a.
Klain, B. I., and N. A. Kurazhkovskaya, The fractal characteristics of the long-period np pulsations in magnetoconjugated regions, Geophys. Res. Abstr., 2, 781, 2000b.
Klain, B. I., and N. A. Kurazhkovskaya, North-South asymmetry in the fractal properties of irregular np pulsations, Geomagn. Aeron. (in Russian), 41 (4), 445, 2001.
Kleimenova, N. G., O. V. Bolshakova, V. A. Troitskaya, and E. Friis-Christensen, Two types of the long-period geomagnetic pulsations near the boundary of the dayside polar cusp, Geomagn. Aeron. (Engl. Transl.), 25 (1), 139, 1985.
Korn, G. A., and T. M. Korn, Mathematical Handbook for Scientists and Engineers (in Russian), 720 pp., Nauka, Moscow, 1968.
Kurazhkovskaya, N. A., and B. I. Klain, Dynamics of long-period irregular pulsations at high latitudes during strong magnetic storms, Geomagn. Aeron. (in Russian), 35 (6), 53, 1995.
Loewe, C. A., and G. M. Proelss, Classification and mean behavior of magnetic storms, J. Geophys. Res., 102, 14,209, 1997.
Mundt, M. D., W. B. Magoire, and R. R. P. Chase, Chaos in the sunspot cycle: Analysis and prediction, J. Geophys. Res., 96, 1705, 1991.
Nakagawa, M., A critical exponent method to evaluate fractal dimensions of self-affine data, J. Phys. Soc. Jpn., 62 (12), 4233, 1993.
Nishida, A., Geomagnetic Diagnosis of the Magnetosphere (in Russian), 300 pp., Mir, Moscow, 1980.
Otnes, R. K., and L. Enochson, Applied Time Series Analysis (in Russian), 428 pp., Mir, Moscow, 1982.
Troitskaya, V. A., and O. V. Bolshakova, Diagnostics of the magnetosphere using multipoint measurements of ULF-waves, Adv. Space Res., 8 (9), 413, 1988.
Vassiliadis, D. V., et al., Low-dimensional chaos in magnetospheric activity from AE time series, Geophys. Res. Lett., 17 (11), 1841, 1990.
Voros, Z., Synergetic aspects of geomagnetic indices, Geophys. Trans., 36 (3-4), 347, 1991.