
Yu. P. Maltsev and A. A. Ostapenko
Polar Geophysical Institute, Apatity, Russia
The magnetospheric magnetic field is
 | (1) |
where B int is the field due to currents inside the Earth and B ext is the field produced by magnetospheric currents. The internal field B int is rather stable; the external field B ext exhibits a strong variability. In particular, magnetic storms are accompanied by considerable variations in the magnetospheric magnetic field. The main characteristic of a magnetic storm is the hourly Dst index defined as the H component of the magnetic disturbance averaged over magnetograms of several low-latitude observatories located at different longitudes. The Dst index anticorrelates with the AE, AL, and Kp indexes which serve mainly to measure the substorm activity.
It is impossible to build a detailed distribution of the external magnetospheric field during a particular storm because of an insufficient number of spacecraft, and, therefore, we are limited to statistical studies. In previous works the external field was studied in relation with the other than Dst indexes or with the Dst index, but in separate limited magnetospheric regions. For instance, Sugiura and Poros [1973] considered the field at 3-23 RE for quiet ( Kp = 0-1 ) and slightly disturbed ( Kp = 2-3 ) conditions. In the inner magnetosphere ( r < 5 RE at noon and r < 10 RE at midnight) the external field was found to be directed preferentially in the negative z direction (in the SM coordinate system). A similar result was obtained by Mead and Fairfield [1975], who approximated the external field at the distances from 4 RE to 17 RE by second-degree polynomials in the geocentric distance.
The dependence of the field on the Dst index was analyzed in the equatorial plane at 2.3-3.6 RE only. For these distances the empirical relation for the field averaged over longitude was obtained [Sugiura, 1973]
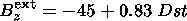 | (2) |
The external field at 4-8.8
RE near the equatorial plane was
plotted by
Iijima et al. [1990]
for long disturbed periods
( 2 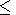 Kp
Kp 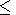 6,
-70
6,
-70 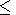 Dst
Dst 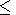 -20 nT). A strong azimuthal
field inhomogeneity which is likely to be due to the fact that the
current in the nightside magnetosphere is by a factor of 2 or
3 stronger than in the dayside magnetosphere was discovered.
-20 nT). A strong azimuthal
field inhomogeneity which is likely to be due to the fact that the
current in the nightside magnetosphere is by a factor of 2 or
3 stronger than in the dayside magnetosphere was discovered.
Ostapenko and Maltsev [1997] approximated the fields at 3-10 RE by the forth-degree polynomial in the geocentric distance. The polynomial coefficients were sought for as a linear combination of Dst and Kp indexes, dynamic solar wind pressure, and vertical IMF component. The dependence on Dst proved to be similar to that described by (2). With increasing distance from the Earth the dependence on Dst becomes weaker and at r = 10 RE it is negligibly weak. Earlier a similar result was obtained by Fairfield et al. [1987] for dependence of the external field on the Kp value.
So far the statistical dependence of the tail lobe field on the Dst index has not been studied. It was found that the tail lobe field grows with the AE index [Baumjohann et al., 1990]; the AL index [Nakai et al., 1991]; the southward IMF component [Fairfield and Jones, 1996; Nakai et al., 1991]; and dynamic solar wind pressure [Fairfield and Jones, 1996; Nakai et al., 1991; Ostapenko and Maltsev, 1998].
Up until now, the field variations caused by a storm have not been studied for the entire magnetosphere. The goal of this work was to investigate the response of the magnetic field at distances -30 RE < x < 10 RE; -15 RE < y < 15 RE; and -15 RE < z < 15 RE to changes in the Dst index.
The database described by Fairfield et al. [1994] was used. It includes more than 70,000 three-component magnetic field measurements carried out by 11 satellites in the region from 3 to 60 RE during 20 years. All the magnetic field measurements are supplemented by hourly Dst indexes and 3-hour values of the Kp index. Sixty-seven percent of the data are complemented by hourly averages of the dynamic solar wind pressure p and three IMF components. For 47% of the data in the database, an hourly AE index is also given.
We used the data for the region -30 RE < x < 10 RE, y < 15 RE, and z < 15 RE. Depending on the Dst value, the initial data set was divided into three subsets. Table 1 shows the number of data points N in each subset and average values of Dst, Kp, AE, p, and IMF Bz. For each subset the external magnetic field was averaged over a three-dimensional mesh with the side length of 4 RE.
In averaging, the dawn-dusk and north-south symmetries were taken into account. For distances x > -10 RE, the SM coordinate system with the z axis antiparallel to the Earth dipole axis was used. For distances x < -10 RE, in the magnetotail, the GSM coordinate system with the x axis pointed toward the Sun was employed. To improve spatial resolution in the vicinity of the neutral sheet which experiences considerable variations due to changes in the Earth dipole tilt, we introduced the coordinate z = z GSM - z ns, where z GSM is the solar-magnetospheric coordinate and z ns is the coordinate of the neutral sheet determined from the expression [Peredo et al., 1993]
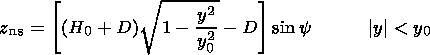 |
where y is the Earth dipole tilt angle, H0 = 9 RE, D = 7 RE, and y0 = 13.5 RE.

|
| Figure 1 |
|
| Figure 2 |

|
| Figure 3 |

|
| Figure 4 |

|
| Figure 5 |

|
| Figure 6 |
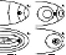
|
| Figure 7 |
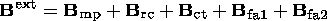 | (3) |
The fields of the currents at the magnetopause, ring current, tail current and field-aligned currents of zones 1 and 2 are in the right-hand side of formula (3), respectively. The fields of each of these currents in the noon-midnight meridian plane are schematically shown in the right-hand side of Figure 7.
Comparing Figure 1
to the right-hand side of Figure 7, one can
see that the effect of the tail currents
B ct
dominates at any level of
magnetic activity. Only in the vicinity of the daytime
magnetopause the field of the currents at the magnetopause
B mp
prevails. The effect of the ring current
B rc
is slightly pronounced.
It is manifested evidently in the increase of the depression while
approaching the Earth (Figure 2). The effect of the field-aligned
currents B
fa1 and B
fa2
is manifested even weaker.
Figures 3
and 4
show that the magnetic field in the tail lobes
increases at the depression increase during a storm. It indicates to
an intensification of the tail currents.
Figure 5 shows that the most considerable increase of
Bx during
a storm occurs in the near-Earth part of the tail lobes at
x = 0. This
means that the closest part of the tail current is intensified. It is
worth noting that according to Figure 7 the ring current gives
( B
rc)x = 0 in the
x = 0
plane. One may expect that the field-aligned
currents of zone 1 (entering the ionosphere in the morning and
leaving in the evening) are also intensified during a storm. The
x component of the field of the field-aligned and tail currents is of
the same sign above the Earth poles (see Figure 7). At
the
magnetic shells located deeper than the field-aligned current the
Bx component induced by the field-aligned current changes
its sign,
thus reducing the field in the low-latitude parts of the nearest tail
lobe. Thus, the field-aligned current leads to a irregularity of the
magnetic field in the nearest lobe. This irregularity is seen in the
top part of Figure 5. However it is not well pronounced and this
means that the tail currents produce stronger effect in the
x = 0
plane than the field-aligned currents.
The field-aligned currents of zone 2 short-circuited
to the
partially-ring current should also be intensified during a storm.
The magnetic field of the given current system is in a way similar
to the fields formed by the tail and ring currents.
Usually it is accepted that the total field-aligned current of
zone 2 is about 70% of the zone 1 currents. Since no effects of the
zone 1 currents are seen in
Figures 1,
2,
3,
4,
and 5,
the zone 2 field-aligned
currents hardly impact considerably on the field distribution in the
magnetosphere. The
By component of the external field almost does
not depend on
Dst at the distance
x = - 20 RE (Figure 3). A weak
dependence on
Dst appears at the distance
x = -10 RE
(Figure 4).
In the
x = 0 plane passing though the center of the Earth, the
dependence of the
By component on the storm intensity is very
strong (Figure 5).
The magnetic depression occurs in the major part of the
magnetospheric equatorial plane at all activity levels (see Figure 2).
With an increase of the storm activity the depression becomes
deeper and covers more distant regions. The epicenter of
the
depression is shifted relative to the Earth center by about
3 RE towards the nightside. It should be noted that there
is no
measurements at the distances less than
3 RE so the isolines in this
region in Figure 2
are a result of an interpolation.
Sugiura [1973]
studied the field in the equatorial plane at distances of
2.3-3.6 RE.
For the field averaged over longitudes the empirical relation (2)
was obtained.
Iijima et al. [1990]
drew a distribution of the field in
the vicinity of the equatorial plane at distances of
4-8.8 RE for the
-70  Dst
Dst  - 20 nT
conditions at the mean value
Dst = - 34 nT.
The field distribution in Figure 2 resembles the field obtained in
the above-mentioned publications but differs by better smoothness.
Apparently it is due to the fact that we have averaged the field
within larger sells. Otherwise there would not be enough data to
derive the field dependence on the
Dst index in the entire volume
of the magnetosphere. The differential field shown in Figure 6
most of all resembles the B
ct
field in Figure 7.
This means that at
the storm intensification mainly the tail current is increased.
- 20 nT
conditions at the mean value
Dst = - 34 nT.
The field distribution in Figure 2 resembles the field obtained in
the above-mentioned publications but differs by better smoothness.
Apparently it is due to the fact that we have averaged the field
within larger sells. Otherwise there would not be enough data to
derive the field dependence on the
Dst index in the entire volume
of the magnetosphere. The differential field shown in Figure 6
most of all resembles the B
ct
field in Figure 7.
This means that at
the storm intensification mainly the tail current is increased.
Variations in the external magnetic field at distances up to 30 RE have been studied as a function of storm intensity. It has been shown that for all storm activity levels the effect of magnetotail currents dominates. As the storm enhances, the tail current effect becomes stronger. The field due to magnetopause currents prevails in the distant region of the dayside magnetosphere.
Baumjohann, W., G. Paschmann, and H. Luhr, Pressure balance between lobe and plasma sheet, Geophys. Res. Lett., 17, 45, 1990.
Fairfield, D. H., and J. Jones, Variability of the tail lobe field strength, J. Geophys. Res., 101, 7785, 1996.
Fairfield, D. H., M. H. Acuna, L. J. Zanetti, and T. A. Potemra, The magnetic field of the equatorial magnetotail: AMPTE/CCE observations at R < 8.8 RE, J. Geophys. Res., 92, 7432, 1987.
Fairfield, D. H., N. A. Tsyganenko, A. V. Usmanov, and M. V. Malkov, A large magnetosphere magnetic field database, J. Geophys. Res., 99, 11,319, 1994.
Iijima, T., T. A. Potemra, and L. J. Zanetti, Large-scale characteristics of magnetospheric equatorial currents, J. Geophys. Res., 95, 991, 1990.
Mead, G. D., and D. H. Fairfield, A quantitive magnetospheric model derived from spacecraft magnetometer data, J. Geophys. Res., 80, 523, 1975.
Nakai, H., Y. Kamide, and C. T. Russell, Influences of solar wind parameters and geomagnetic activity on the tail lobe magnetic field: A statistical study, J. Geophys. Res., 96, 5511, 1991.
Ostapenko, A. A., and Yu. P. Maltsev, Relation of the magnetic field in the magnetosphere to the geomagnetic and solar wind activity, J. Geophys. Res., 102, 17,467, 1997.
Ostapenko, A. A., and Yu. P. Maltsev, Three-dimensional magnetospheric response to variations in the solar wind dynamic pressure, Geophys. Res. Lett., 25, 261, 1998.
Peredo, M., D. P. Stern, and N. A. Tsyganenko, Are existing magnetospheric models excessively stretched?, J. Geophys. Res., 98, 15,343, 1993.
Sugiura, M., Quiet time magnetospheric field depression at 2.3-3.6 RE, J. Geophys. Res., 78, 3182, 1973.
Sugiura, M., and D. J. Poros, A magnetospheric field incorporating the Ogo 3 and 5 magnetic field observations, Planet. Space Sci., 21, 1763, 1973.