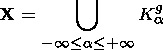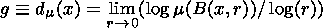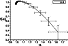International Journal of Geomagnetism and Aeronomy
Vol. 3, No. 2, December 2002
Recovering
data
gaps
through neural network methods
A. Gorban and A. Rossiev
Institute of Computational Modeling, Krasnoyarsk, Russia
N. Makarenko and Y. Kuandykov
Institute of Mathematics, Almaty, Kazakhstan
V. Dergachev
Ioffe Physical and Technical Institute, St. Petersburg, Russia
Contents
Abstract
A new method
is presented to recover the lost
data in geophysical time series.
It is clear that gaps in data
are a substantial problem in obtaining correct outcomes about phenomenon
in time series processing. Moreover, using the data with
irregular coarse steps results in the loss of prime information
during analysis. We suggest an approach to solving these problems,
that is based on the idea of modeling the data with the help of
small-dimension
manifolds,
and it is implemented with the help of
a neural network. We use this approach on real data and show
its proper use for analyzing time series of cosmogenic
isotopes. In addition, multifractal analysis was applied to
the recovered 14C concentration in the Earth's atmosphere.
1. Introduction
It is well known that
the dynamics of
most global processes under
investigation have a
long time range.
So, to study them properly
requires good data sets.
Data here
are represented by means of historical time series of cosmogenic
isotopes
14C and
10Be,
and
a number
of natural characteristics such as Wolf numbers,
AA index,
and other
indexes
are associated with them.
Here, the term "good data samples" denotes long range,
equidistant, solid data without gaps, but because of imperfection
of astronomical tools
that were used by researchers over the
years, the inadequacy of these time series for strict
scientific investigation is typical.
Since the recovery itself serves not only to restore
important lost information but
also to process
data
gained
as well, we suppose
the multifractal analysis and time series processing are useful
for demonstrating that statement. So, to further
clarify such problems influence on the whole application
area of time series analysis, let us consider the details.
The goal of time series analysis is to
ascertain
and
describe
the nature of
sources that
produce signals. As a rule, the information consisting in
a time series frequently
contains different processes with
different scales of coherence. In many cases,
correlation structure
of the time series specifies the resulting property of stochastic
self-similarity,
that is, invariance under the group of affine
transformations
X  arX,
t
arX,
t  rt, where
ar is a random variable
[Veneziano, 1999].
The values having
stochastic self-similarity properties are often considered as
multifractal measures, which are described with the help of scaling
exponents
[Falconer, 1994],
characterizing singularities, and
irregular structures. It is important to study the irregular
structures to infer properties about the underlying physical
phenomena
[Davis et al., 1994a].
Until recently, the Fourier
transform was the main mathematical tool for analyzing
singularities
[MacDonald, 1989].
The Fourier transform is global
and describes the overall regularity of signals,
but it is not well adapted for finding the location and spatial
distribution of singularities. That was the major motivation
for studding the wavelet transform
in applied domains
[Davis et al., 1994b].
By decomposing signals into elementary building
blocks, which are well localized both in space and time, the
wavelet transform can characterize the local regularity of signals.
rt, where
ar is a random variable
[Veneziano, 1999].
The values having
stochastic self-similarity properties are often considered as
multifractal measures, which are described with the help of scaling
exponents
[Falconer, 1994],
characterizing singularities, and
irregular structures. It is important to study the irregular
structures to infer properties about the underlying physical
phenomena
[Davis et al., 1994a].
Until recently, the Fourier
transform was the main mathematical tool for analyzing
singularities
[MacDonald, 1989].
The Fourier transform is global
and describes the overall regularity of signals,
but it is not well adapted for finding the location and spatial
distribution of singularities. That was the major motivation
for studding the wavelet transform
in applied domains
[Davis et al., 1994b].
By decomposing signals into elementary building
blocks, which are well localized both in space and time, the
wavelet transform can characterize the local regularity of signals.
Real records are contaminated with noise, which is rarely additive,
Gaussian, or white. Often, noisy
data are generated by
nonlinear chaotic processes, which can produce time series having
periodic, quasi periodic, and chaotic patterns
[Abarbanel et al., 1993].
All
of these factors lead to complex, nonlinear, and nonstationary
cosmogenic time series. The investigation of such data is not
trivial. For time series that arise from chaotic systems of low
dimension, there are certain quantities,
for example, the
dimension of the
attractor or the Lyapunov exponents that can be obtained using
up-to-date topology tools
[Sauer et al., 1991].
The values are
especially interesting because they characterize intuitively useful
concepts,
for example, the
number of active degrees of freedom or the rate of
divergence of nearby trajectories for underlying physical systems.
Algorithms for estimating these quantities are available. If we
cannot assume the existence of underlying low dimension dynamics, we
can use the Wold decomposition
[Anderson, 1971]
time series.
The Wold theorem states that any (linear or nonlinear) stationary
zero-mean process can be decomposed into the sum of two
non-correlated components: deterministic and nondeterministic.
It follows from the theorem that any stationary process can be
modeled as an autoregressive moving-average (ARMA models).
However, almost
all methods of time series analysis, whether traditional linear or
nonlinear, must assume some kind of stationarity. Testing the
nonstationarity of time series is a difficult task
[Schreiber, 1997],
and a number of statistical tests of the stationarity have been
proposed in the literature. If it is absent, one could expect that
the differentiation of time series can remove nonstationarity in
the mean. Another way is to divide data into segments over which
the process is essentially stationary and then use the wavelet
scale spectrum to estimate the parameters of the time series
[Bacry et al., 1993].
Thus, investigators now have a few tools for
analyzing complex data. Nevertheless, to apply these techniques one
should have enough long, equidistant time series;
however, such
cosmogenic data do not exist.
Besides the short length of historical time
series,
another substantial problem remains:
how to obtain correct
results about phenomenon in a time series if there are no
fragments of data, as is typical for cosmogenic isotope data.
Non-equidistant data distorts even ordinary statistic
characteristics. Traditional methods of filling gaps are not
highly
effective for nonstationary and nonlinear time series
[Little and Rubin, 1987].
When
a great number of
data are
missed
and
when their location is random, there is no solution to this problem.
We suggest some approaches for solving the problems of recovering
missed data in time series based on neuromathematical methods.
The structure of this paper is
as follows.
In Section 2 we give a full description of the
proposed method and, moreover, we state the conception of
the model construction using this method. In Section 3,
we
discuss our results
after applying such models to
14C,
10Be isotope,
and Wolf index data recovery;
we also define multifractal analysis and
its application to
14C isotope data recovery. The
summary is found in the conclusion.
2. Recovering Missing Data by Neuromathematical Methods
In this section, we discuss a new neural non-linear approach to the
problem of gap recovery
[Gorban et al., 1998;
Rossiev, 1998].
The method is founded on Anzatz reasoning, and it
only one
allows
to obtain plausible values of missed data.
However, the testing of time series with artificial holes
has shown a good result. So, a method of modeling data with gaps by
using a sequence of curves has been developed. The method is a
generalization of iterative construction of singular expansion of
matrices with gaps
[Hastie and Stuetzle, 1988;
Kramer, 1991].
2.1. The Model
The idea of modeling data with the help of manifolds of small
dimension was conceived a long time ago. The most widespread,
oldest, and feasible implementation for modeling
data without gaps is the
classical method of principal components. The method calls for
modeling the data by their orthogonal projections over "principal
components" -- eigen vectors of the correlation matrix with
corresponding largest eigen values. Another algebraic
interpretation of the principal component method is a singular
expansion of the data table. Generally, to present data with
sufficient accuracy requires relatively few principal components.
Imagine a table of data
A={aij}; its rows correspond to
objects, and its columns correspond to features. Then, let a portion
of information in the table be missing. Let us
look at the object
x whose features are represented in a
vector form ( x1, x2,...,xn ).
There may be
k gaps in
the vector
x,
that is, some components of
x are lost. We suppose
that this vector is represented as a
k dimensional linear
manifold
Lk, parallel to
k coordinate axes corresponding to
the missing data. Under a priori restrictions on the missing values
instead of
Lk, we use a rectangular parallelepiped. A manifold
M of a given small dimension (in most cases a curve)
approximating the data in the best way and satisfying certain
regular conditions is sought. For the complete vectors of
data, an accuracy of approximation is determined as a regular
distance from a point to a set (the lower bound of the distances to
the points of the set). For the incomplete data,
the lower bound of the distances between the points of
M and
Lx (or, accordingly,
Pk ) may be used.
From the data closest to
them, points of
M are subtracted.
We obtain a residue, and the
process is repeated until the residues are close enough to zero.
Proximity of the linear manifold
Lk, or parallelepiped
Pk,
to zero means that the distance from zero to the point of
Lk (accordingly,
Pk ), which is closest to it is small. Desired
approximation can be constructed recursively
[Gorban et al., 2000;
Rossiev, 1998]
for three models: linear, quasilinear, or essentially
non-linear (self-organizing curves (SOC)). We illustrate the idea
using an example of a
linear model. Let there be a rectangular table
A={aij}, the cells of which are filled with real
numbers or
with some symbol @ denoting absence of data. The problem is to
approximate
A with a matrix
P1 in a form of
xiyj+bj,
by means of the least squares method
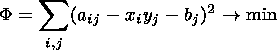 | (1) |
where
aij @.
If there are any two known vectors, then the
third one will be calculated through
explicit formulas. As a result, for
the given matrix
A,
we will find the best approximation,
that is the
matrix
P1. Further on, we look for a matrix,
P2,
that is the best approximation of
A-P1 and so on, while the
norm of
A is not sufficiently close to zero. Thus, the initial
matrix
A is presented in the form of a sum of matrices of rank 1,
that is,
A=P1+P2+
@.
If there are any two known vectors, then the
third one will be calculated through
explicit formulas. As a result, for
the given matrix
A,
we will find the best approximation,
that is the
matrix
P1. Further on, we look for a matrix,
P2,
that is the best approximation of
A-P1 and so on, while the
norm of
A is not sufficiently close to zero. Thus, the initial
matrix
A is presented in the form of a sum of matrices of rank 1,
that is,
A=P1+P2+  +Pq. The
Q factorial recovering of the
gaps consists in their definition through the sum of matrices
Pq. For incomplete data after a number of iterations, we
get a
system of factors that we will use for recovery. Further, we
again construct a system of factors with the help of already
recovered data and so on.
+Pq. The
Q factorial recovering of the
gaps consists in their definition through the sum of matrices
Pq. For incomplete data after a number of iterations, we
get a
system of factors that we will use for recovery. Further, we
again construct a system of factors with the help of already
recovered data and so on.
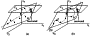
|
|
Figure 1
|
Geometrical interpretation of a linear model is shown in
Figure 1a,
for
A  R2. We considered
our example in
R3 space, so our data point
x is presented as
(x1,x2,x3).
Imagine there is a point and that two of its
coordinates are lost (we have only
x3 coordinate), so a plane,
Lk, corresponds to it. The plane
Lk is modeled by the
vector y that is an inclined line approximating known data in a
best manner; vector x
is a set of projections of initial data on
y (
R2. We considered
our example in
R3 space, so our data point
x is presented as
(x1,x2,x3).
Imagine there is a point and that two of its
coordinates are lost (we have only
x3 coordinate), so a plane,
Lk, corresponds to it. The plane
Lk is modeled by the
vector y that is an inclined line approximating known data in a
best manner; vector x
is a set of projections of initial data on
y (  M ). The lost coordinate now is
substituted by the
intersection
Lk
M ). The lost coordinate now is
substituted by the
intersection
Lk  M.
M.
Quasilinear models
[Gorban et al., 2000;
Rossiev, 1998]
are
based on the algorithm of linear model construction described
above. First, we construct a linear model, then the vector-function
f(t) (a cubic spline or a polynomial) that minimizes the
functional:
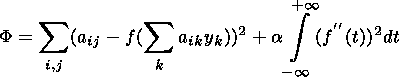 | (2) |
where
a>0 is a smoothing parameter.
So, first we are
looking for the projection of data vector
a on a manifold of
small dimension
y:
Pr(a)=ty+b,
t=(a,y), then we find a point
on the curve
f(t). For incomplete data,
the closest point
t(a) is taken on the manifold. And after that, we take the corresponding
point on the curve
f(t ) for
t=t(a). After construction of
f(t), the matrix
A is substituted by the matrix of deviations
from the model (Figure 1b). The process is repeated several times,
and at the end the initial table,
A is represented in a form of
Q factorial model:
aij
 i,jfi(tj).
i,jfi(tj).
The
third model is based on the Kohonen self-organizing maps theory or,
more exactly, on the paradigm of self-organizing curves. These
curves are defined by a set of points (a kernel) situated on a
curve (at the first approach this curve is a polygonal one), on
which a set of data point (taxon) must be mapped. Under fixed
decomposition of the data set on taxons, the SOC is constructed
uniquely. Under fixed location of kernels, taxons are easily
constructed, too, with the help of minimizing of some functional,
which consists of three addends: a measure of the best
approximation, a measure of connectedness, and a measure of
nonlinearity
[Gorban et al., 2000].
Successive searching; kernels
 taxons
taxons
 kernels
kernels
 ... leads
to the convergence of the algorithm. The computational process is
implemented on the neural conveyor Famaster 2 made by Gorban's team
at the Institute of
Computational Mathematics of
the Siberian Division of the
Russian Academy of Sciences.
... leads
to the convergence of the algorithm. The computational process is
implemented on the neural conveyor Famaster 2 made by Gorban's team
at the Institute of
Computational Mathematics of
the Siberian Division of the
Russian Academy of Sciences.
3. Results
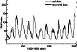
|
|
Figure 2
|
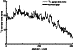
|
|
Figure 3
|
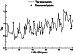
|
|
Figure 4
|
We carried out the experiments with different time series. The
results of some experiments are shown in Figure 2.
About 50% of the points in the annual Wolf number
time series
were delete. For gap recovery, we used the SOC model. Strings of
the initial data table were F. Takens
m dimensional delay
vectors
[Sauer et al., 1991].
The time delay equals 1, and the
embedding dimension equals 6.
The strings look as
follows:
akj=xk,xk+1,...,xk+5.
The embedding
dimension was estimated with the help of
the
False Nearest Neighbours' (FNN) method
[Abarbanel et al., 1993].
Thus, deleting a point in a time series implied
deleting the whole diagonal corresponding to that point. As
you can see, the neural conveyor
even
recovered
the peaks of
cycles well.
Figure 3
shows a fragment of the cosmogenic isotope
14C time series. The whole time series
ranges from 5995 BC to 1945 AD. We give only the results recovering
30% of deleted points of the fragment from 5995 BC to 10 AD.
And the last time series used in our experiment was
10Be
(1428-1999 AD, annual data),
and
about 10%
of points
were deleted
(Figure 4).
Some results of recovery (in
numerical form) are provided in Table 1.
The
construction of the initial table by F. Takens
(unlike the arbitrary method
of construction mentioned in
Gorban et al. [[2000];
Rossiev [1998]
essentially changes the situation. Really, a
lost value of
y component of the vector on Figure 1a induces a
gap of
x component in the next (by F. Takens) vector. The
intersection of two lines recovers a missed value. In the
multidimensional case, the problem is reduced to the search of
a transverse intersection of hyperplanes
[Sauer et al., 1991].
Thus,
the method of gap recovery takes on a formal context.
3.1. Multifractal Spectrum of \boldmath
<UNDEF>14 C Time Series
After
applying the
recovery
procedure
to the time
series, we had an equidistant and complete one, so it became
possible to use more refined tools to implement our investigations.
We used an approach in which time series is considered as
multifractal random measures.
Remember
[Barreira et al. 1997]
that multifractal spectrum of singularities of Borel finite measure
m on a compact set
X is a function
f(a) defined by a pair
(g,G). Here,
g:X [-
[- ,+
,+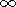 ] is a function, which determines
the level sets:
g:Kag={x
] is a function, which determines
the level sets:
g:Kag={x
 X:g(x)=a
} and produces a
multifractal decomposition
X:
X:g(x)=a
} and produces a
multifractal decomposition
X:
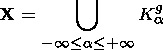 |
Let
G be a real function, which is defined on
Zi X such that
G(Z1)2) if
Z1
X such that
G(Z1)2) if
Z1 Z2. Then
multifractal spectrum is
f(a)=G(Kag).
Let
g be
determined as pointwise dimension
dm of measure
m at all
points
x
Z2. Then
multifractal spectrum is
f(a)=G(Kag).
Let
g be
determined as pointwise dimension
dm of measure
m at all
points
x X for which the limit
X for which the limit
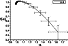
|
|
Figure 5
|
exists, where
m(B(x,r)) is a "mass" of
measure in the ball of
radius
r centered at
x. Since we have chosen
g=dm, we
can omit the subscript from further references to
Kag.
Then
Ka={x:dm(x)=a},
where the exponent is a
local density of
m. The singular distribution
m can then be
characterized by Hausdorff dimension of
Ka, that is,
f(a)=G(Ka)=
dimH(Ka). If
m is
self-similar in some sense,
f(a) is a well-behaved concave
function of
f(a) [Falconer, 1994].
To estimate
f(a), we
applied the method of the partition sum
[Riedi, 1997].
For analysis,
annual
14C time series (1510-1954)
was used. Initial time
series had a fragment, where known data values were given in a
period of 2 years (1890.5-1910.5), and there were some real data gaps
(1911-1912, 1914, 1946).
With the help of the method suggested above,
this time series was recovered and became equidistant. Thus,
the time series is applicable for multifractal
analysis. In Figure 5,
a
f(a) -spectrum of
this time series
is shown.
It shows that
14C records have multifractal
properties in a large range of scales (1-2.2).
4. Conclusion
Our experiments have shown that the neural method for gap
recovery in a time series is quite eligible for analyzing
cosmogenic isotopes. This method allows
equidistant time
series
to be obtained,
which can be researched by using the modern tools of
non-linear analysis.
References
Abarbanel, H. D. I., R. Brown, J. J. Sidorowich, and
L. Sh. Tsimring,
The analysis of observed chaotic data in physical
systems,
Rev. Mod. Phys., 65 (4), 1331, 1993.
Anderson, T. W.,
The Statistical Analysis of Time Series, Wiley, New York, 1971.
Bacry, E., J. F. Muzy, and A. Arnedo,
Singularity spectrum
of fractal signals from wavelet analysis: Exact results,
J. Statist. Phys., 70 (3/4), 635, 1993.
Barreira, L., Y. Pesin, and J. Schmeling,
On a general
concept of multifractality: Multifractal spectra for dimensions,
entropies, and Lyapunov exponents. Multifractal rigidity,
Chaos, 7 (1), 27, 1997.
Davis, A., A. Marshak, W. Wiscombe, and R. Cahalan,
Multifractal characterizations of nonstationarity and intermittence
in geophysical fields: Observed, retrieved, or simulated,
J. Geophys. Res., 99 (D4), 8055, 1994a.
Davis, A., A. Marshak, and W. Wiscombe,
Wavelet-based
multifractal analysis of nonstationary and/or intermittent
geophysical signals,
in Wavelets in Geophysics,
edited by Efi Foufoula-Georgiou and Praveen Kumar,
249 pp., Academic Press, New York, 1994b.
Falconer, K. J.,
The Multifractal spectrum of
statistically self-similar measures,
J. Theor. Probab., 7 (3), 681, 1994.
Gorban, A. N., S. V. Makarov, and A. A. Rossiev,
Neural
conveyor to recover gaps in tables and construct regression by
small samplings with incomplete data,
Mathematics, Computer, Education (in Russian), 5 (II), 27, 1998.
Gorban, A. N., A. A. Rossiev, and D. C. Wunsch II,
Self-organizing curves and neural modeling of data with gaps,
Proceeding of Neuroinformatics 2000 (in Russian),
Part 2, p. 40,
Moscow,
2000.
Hastie, T., and W. Stuetzle,
Principal curves, J. Am. Stat. Assoc., 84 (406),
502,
1988.
Kramer, M. A., Non-linear principal component analysis
using autoassociative neural networks,
AIChE J., 37 (2), 233, 1991.
Little, R. J. A., and D. B. Rubin,
Statistical Analysis With Missing Data,
John Wiley & Sons, Inc., New York, 1987.
MacDonald, G. J., Spectral analysis of time series
generated by nonlinear processes,
Rev. Geophys., 27 (4), 449, 1989.
Riedi, R. H.,
An Introduction to Multifractals,
Rice University, 1997.
Rossiev, A. A., Modeling data by curves to recover the
gaps in tables,
Nueroinformatics Methods, 6, KGU Publishers,
Krasnoyarsk, 1998.
Sauer, T., J. A. Yorke, and M. Casdagli,
Embedology,
J. Stat. Phys., 65 (3/4), 579, 1991.
Schreiber, T., Detecting and analyzing nonstationarity in
time series using nonlinear cross predictions,
Phys. Rev. Lett., 78 (5), 843, 1997.
Veneziano, D., Basic properties and characterization of
stochastically self-similar processes,
Rd. Fractal., 7 (1), 59, 1999.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on December 8, 2002.
 arX,
t
arX,
t  rt, where
ar is a random variable
[Veneziano, 1999].
The values having
stochastic self-similarity properties are often considered as
multifractal measures, which are described with the help of scaling
exponents
[Falconer, 1994],
characterizing singularities, and
irregular structures. It is important to study the irregular
structures to infer properties about the underlying physical
phenomena
[Davis et al., 1994a].
Until recently, the Fourier
transform was the main mathematical tool for analyzing
singularities
[MacDonald, 1989].
The Fourier transform is global
and describes the overall regularity of signals,
but it is not well adapted for finding the location and spatial
distribution of singularities. That was the major motivation
for studding the wavelet transform
in applied domains
[Davis et al., 1994b].
By decomposing signals into elementary building
blocks, which are well localized both in space and time, the
wavelet transform can characterize the local regularity of signals.
rt, where
ar is a random variable
[Veneziano, 1999].
The values having
stochastic self-similarity properties are often considered as
multifractal measures, which are described with the help of scaling
exponents
[Falconer, 1994],
characterizing singularities, and
irregular structures. It is important to study the irregular
structures to infer properties about the underlying physical
phenomena
[Davis et al., 1994a].
Until recently, the Fourier
transform was the main mathematical tool for analyzing
singularities
[MacDonald, 1989].
The Fourier transform is global
and describes the overall regularity of signals,
but it is not well adapted for finding the location and spatial
distribution of singularities. That was the major motivation
for studding the wavelet transform
in applied domains
[Davis et al., 1994b].
By decomposing signals into elementary building
blocks, which are well localized both in space and time, the
wavelet transform can characterize the local regularity of signals.
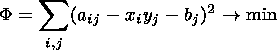
 @.
If there are any two known vectors, then the
third one will be calculated through
explicit formulas. As a result, for
the given matrix
A,
we will find the best approximation,
that is the
matrix
P1. Further on, we look for a matrix,
P2,
that is the best approximation of
A-P1 and so on, while the
norm of
A is not sufficiently close to zero. Thus, the initial
matrix
A is presented in the form of a sum of matrices of rank 1,
that is,
A=P1+P2+
@.
If there are any two known vectors, then the
third one will be calculated through
explicit formulas. As a result, for
the given matrix
A,
we will find the best approximation,
that is the
matrix
P1. Further on, we look for a matrix,
P2,
that is the best approximation of
A-P1 and so on, while the
norm of
A is not sufficiently close to zero. Thus, the initial
matrix
A is presented in the form of a sum of matrices of rank 1,
that is,
A=P1+P2+  +Pq. The
Q factorial recovering of the
gaps consists in their definition through the sum of matrices
Pq. For incomplete data after a number of iterations, we
get a
system of factors that we will use for recovery. Further, we
again construct a system of factors with the help of already
recovered data and so on.
+Pq. The
Q factorial recovering of the
gaps consists in their definition through the sum of matrices
Pq. For incomplete data after a number of iterations, we
get a
system of factors that we will use for recovery. Further, we
again construct a system of factors with the help of already
recovered data and so on.
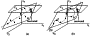
 R2. We considered
our example in
R3 space, so our data point
x is presented as
(x1,x2,x3).
Imagine there is a point and that two of its
coordinates are lost (we have only
x3 coordinate), so a plane,
Lk, corresponds to it. The plane
Lk is modeled by the
vector y that is an inclined line approximating known data in a
best manner; vector x
is a set of projections of initial data on
y (
R2. We considered
our example in
R3 space, so our data point
x is presented as
(x1,x2,x3).
Imagine there is a point and that two of its
coordinates are lost (we have only
x3 coordinate), so a plane,
Lk, corresponds to it. The plane
Lk is modeled by the
vector y that is an inclined line approximating known data in a
best manner; vector x
is a set of projections of initial data on
y (  M ). The lost coordinate now is
substituted by the
intersection
Lk
M ). The lost coordinate now is
substituted by the
intersection
Lk  M.
M.

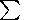 i,jfi(tj).
i,jfi(tj).
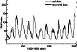
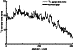
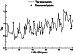
 ,+
,+ X:g(x)=a
} and produces a
multifractal decomposition
X:
X:g(x)=a
} and produces a
multifractal decomposition
X: