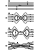
V. S. Semenov, O. A. Alexandrova
Institute of Physics, St. Petersburg State University, St. Petersburg, Russia
N. V. Erkaev
Institute of Computational Modelling, Russian Academy of Sciences, Russia
S. Mühlbachler, H. K. Biernat
Space Research Institute, Austrian Academy of Sciences, Graz, Austria
also at Institute for Geophysics, Astrophysics, and Meteorology, University of Graz, Graz, Austria
From the theoretical point of view, the magnetosphere is a direct result of impenetrability or frozen-in magnetic field condition of two highly conducting magnetoplasmas. Hereby, the magnetopause can be interpreted as a tangential discontinuity across which pressure is in balance. Hence, as investigated first by Mead and Beard [1964], the standoff distance of the magnetopause can be determined from pressure balance. More specifically, the magnetopause is located at a distance where the planetary magnetic field pressure (the particles make only a negligible contribution) equals the dynamic pressure of the solar wind (neglecting the small contribution of the interplanetary magnetic field (IMF)). It is clear that when parameters defining the pressure balance change, the position of the magnetopause will also vary.
It emerges from the above that the primary source of magnetopause motion is a change in dynamic pressure of the solar wind. However, there is another source that makes the magnetopause move earthward even when the dynamic pressure is constant. This phenomenon is called "erosion" and was identified in the 1970s when magnetopause crossings made by the OGO 5 spacecraft were investigated [Aubry et al., 1970; Fairfield, 1971]. Recent observational signatures of erosion in the inner magnetosphere have been reported by Sibeck [1994] and Tsyganenko and Sibeck [1994].
Quite generally, one can say that erosion happens during intervals when the IMF has a persistent southward component, Bz<0. Furthermore, the amount of erosion depends on the strength of this north-south component and can be of the order of 1 RE for every 5 nT Bz negative [Kawano and Russell, 1997]. With this in mind, models of magnetopause shape have been developed that account for both the solar wind dynamic pressure and the IMF Bz component [Petrinec and Russell, 1996; Roelof and Sibeck, 1993; Shue et al., 1997, 1998]. For fixed dynamic pressure, these empirically based models give the displacement of the magnetopause resulting from the IMF Bz.
Since a persistent southward orientation of the IMF is a prerequisite for magnetic reconnection, a physical connection between the erosion and reconnection phenomenon was established. The reconnection process "opens" terrestrial field lines; that is, as a result, magnetic field lines exist with one "end" in the ionosphere and another in the flowing magnetosheath plasma, that is ultimately in the solar wind [Dungey, 1961]. Indeed, many features of erosion can be modeled in terms of a reconnection model. Nevertheless, one can say in general terms that the physics of dayside magnetosphere erosion is still only partially understood.
So far, the analysis of erosion leads only to the identification of several distinct features, which in turn lead to the development of specific model approaches. These can be summarized as follows:
Hence, at present, although various aspects of magnetopause erosion have been studied, a global picture of the detailed physics behind this phenomena awaits elaboration.
A goal of this paper is to analyze the above-mentioned approaches and put them into a global perspective. To correctly understand the effects of magnetospheric erosion, it is necessary -- in our view -- to take into account a variety of interrelated phenomena, including the appearance of the magnetic barrier near the magnetopause, unsteady (bursty) reconnection of the IMF and the magnetospheric magnetic field, and consequences of reconnection such as the penetration of the IMF to the magnetosphere. Only after a careful investigation of all these effects is it possible to analyze pressure balance and investigate erosion phenomenon in detail.
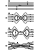
|
| Figure 1 |
Due to the frozen-in condition, the plasma and magnetic field from different sources do not intermix and occupy separate regions, magnetosphere and magnetosheath, for example, and in our simple case, half spaces above and below the current sheet. From the physical point of view, it is clear that free energy cannot be accumulated infinitely by adding magnetic flux from outside and storing it at the current sheet. Eventually, the gradients there become so sharp that the plasma loses the frozen-in property, and this is the starting point for reconnection.
Since current sheets such as the magnetopause are highly non-uniform in nature, it seems reasonable to suppose that the breakdown of the frozen-in approximation occurs locally in the current sheet due to some kind of dissipation mechanism rather than instantaneously throughout the whole length. This natural assumption distinguishes Petschek-type reconnection (local dissipation) from magnetic field annihilation theories such as magnetic field diffusion [Parker, 1963; Sweet, 1958] or the tearing instability [Galeev et al., 1986]. For space and astrophysical applications, pure magnetic field diffusion is too slow to be of interest, but, as was first realized by Petschek [1964], those disturbances can be transmitted through the plasma via large-amplitude MHD waves or shocks. These waves rapidly escape from the dissipative region where reconnection is initiated, transfer the reconnection-associated disturbances to other parts of the current sheet, and establish an outflow region for the plasma streaming toward the current sheet (Figure 1b). Plasma entering the outflow region is accelerated and heated at the slow shocks and then collected inside. The outflow region is also referred to as the field-reversal region, since it connects magnetic field lines across the current sheet, thus establishing a topologically new region of reconnected flux. The leading front of the outflow region is propagated along the current sheet with Alfvén velocity, and therefore the size of the outflow region rapidly outgrows that of the diffusion region, so that the former provides the dominant means of converting and transporting energy and momentum during the reconnection process [Semenov et al., 1983].
So far, we have described the switch-on phase of reconnection, when a dissipative electric field is generated in the diffusion region. But Petschek's wave mechanism does not operate continuously and at all times. At some stage, reconnection should switch off (Figure 1c), in which case no more reconnected flux is added to the system. The slow shocks and the separatrices, which bound the reconnected flux tubes, detach from the former site of diffusion at the time of switch-off. Since the diffusion region no longer acts as a generator of a dissipative electric field and MHD waves, the outflow region will also detach from the reconnection site, and it propagates like a pair of solitary waves in opposite directions along the current sheet. But the outflow region cannot be considered as a soliton, because the slow shocks previously generated continue to propagate toward the edges of the current sheet and to accelerate and heat plasma so that all plasma inside the reconnected tubes bounded by separatrices will be trapped inside the outflow region. Therefore, the outflow region continues to change shape and increase in size even though no more reconnected flux is added.
During the switch-on phase in the immediate vicinity of the diffusion region, the structure of magnetic field and plasma flow is very similar to the original Petschek model (Figure 1b) and, indeed, it can be shown that the time-dependent reconnection solution tends to Petschek's solution in this limit [Pudovkin and Semenov, 1985; Semenov et al., 1983]. So, we can say that our model is an extension of Petschek's wave mechanism for the case of a time-varying reconnection rate. On the other hand, the global structure differs quite a lot from Petschek's picture depicted in Figure 1d, in particular, during the switch-off phase. We believe that a time-dependent reconnection model is more useful for applications than the original Petschek model of steady-state reconnection, since nearly all manifestations of reconnection are strongly time-dependent in nature and even are explosive in character.
We do not know enough about the way in which reconnection is initiated, but we can describe the large-scale consequences of the locally initiated reconnection process by adopting a semi-phenomenological approach. In this approach, we model the initiation introducting a reconnection electric field E*(r,t) inside the diffusion region rather than by specifying a concrete dissipative process. In addition, we assume, like Petschek, that the diffusion region is very small compared to the size of the system, so that in rough approximation, this region corresponds to the so-called reconnection or X-line. By the way, this is an example of a commonly used technique whereby non-ideal effects are lumped into discontinuities to work in the framework of ideal MHD. So, we are describing the diffusion region and the behavior of the dissipative process inside in terms of an initial-boundary condition to solve ideal MHD equations, and this initial-boundary condition corresponds to the specification of the X-line and the behavior of the reconnection rate E*(r,t) along it [Rijnbeek and Semenov, 1993].
The solution of the reconnection problem in an incompressible plasma in the dimensionless form can be presented as follows [Biernat et al., 1987; Pudovkin and Semenov, 1985; Semenov et al., 1983].
 | (1) |
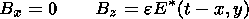 | (2) |
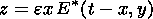 | (3) |
where (1) is the plasma velocity; (2) is the magnetic
field inside the
field reversal region (FRR); (3) is the shape of Petschek shock
for the first quadrant;
E*(t,y) is the electric field along
the reconnection line, or so-called reconnection rate. All quantities
are normalized to the initial magnetic field
B0, the initial
Alfvén velocity
vA=B0/(4pr)1/2,
the length of the
reconnection line
L, the time
L/vA, the pressure
B0/4p,
and the Alfvén electric field
EA=B0vA/c.
Here
e =E*/EA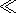 1 is a small parameter.
1 is a small parameter.

|
| Figure 2 |
The first order corrections to the x component of the magnetic field and to the total (gas + magnetic) pressure in the inflow region (IR) can be obtained from the Poisson integrals
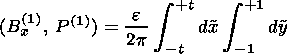 |
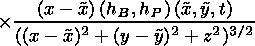 | (4) |
where
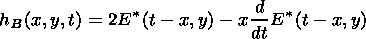 | (5) |
 | (6) |
The whole solution (1)-(6) is defined by the reconnection rate E*(t,y). To model bursty reconnection, we can use series of pulses; one is shown in Figure 2.

|
| Figure 3 |
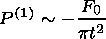 |
where F0 is the reconnected magnetic flux.
Such pressure variations happen from both the magnetosheath (sh) and the magnetosphere (mg) sides of the current sheet for the symmetric model used so far
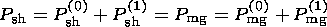 | (7) |
and therefore, they can not lead to motion of the magnetopause. For motion to start, evidently some kind of asymmetry has to appear, and, indeed, physical conditions in the magnetosheath and in the magnetosphere are highly different. First of all, in the magnetosheath there is powerful solar wind flow. Second, there is bow shock at which dynamic pressure remains unchanged at P sh(0)= const for the erosion events under consideration. Therefore, disturbances produced by reconnection at the magnetopause have to propagate against solar wind flow and then reflect from the bow shock. In the magnetosphere, there is neither bow shock nor strong plasma flow; hence, evolution of pressure disturbances produced by reconnection must be different in the magnetosheath and inside the magnetosphere.
Bearing these circumstances in mind, we can believe that total pressure from the magnetosheath side of the diffusion region has to tend to asymptotic value P sh(0)= const more quickly than from the magnetosphere side.
Theoretically,
it is rather difficult to
determine exactly how fast
P sh P sh(0),
but
we can make a simple estimation
for the first consideration.
We suppose that
P sh
P sh(0),
but
we can make a simple estimation
for the first consideration.
We suppose that
P sh P sh(0)
with some characteristic time
t sh, so that
pressure balance at the magnetopause takes the form
P sh(0)
with some characteristic time
t sh, so that
pressure balance at the magnetopause takes the form
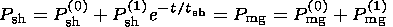 | (7a) |
A pressure pulse decays mostly due to the fast mode wave; therefore,
tsh can be estimated approximately as time propagation
of the
fast wave
vs from subsolar point to the bow shock
t sh=L sh/vs, where
L sh 3RE
is the width of the
magnetosheath. The relaxation time
t sh also
can be
estimated
from the exact solution of unsteady annihilation
[Heyn and Pudovkin, 1993]
or from numerical simulation
[Pudovkin and Samsonov, 1994].
3RE
is the width of the
magnetosheath. The relaxation time
t sh also
can be
estimated
from the exact solution of unsteady annihilation
[Heyn and Pudovkin, 1993]
or from numerical simulation
[Pudovkin and Samsonov, 1994].
The main idea of our model is that the breach in total pressure made by reconnection is closed faster from the magnetosheath side due to the powerful flow of the solar wind than from the magnetosphere side. This leads to an asymmetry in pressure balance and earthward motion of the magnetopause after each pulse of reconnection. The position of the magnetopause can be easily found from (7a)
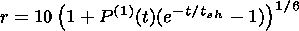 | (8) |
where the variation of total pressure has to be taken from the equation (4), and initial position is supposed to be r=10 RE. We can include N pulses of reconnection with time repetition tr
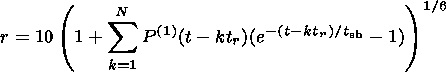 | (9) |
We take the following initial parameters for the numerical calculation: The half-length of the reconnection line is L = 3 RE, the Alfvén velocity is vA=300 km s -1 as average of Alfvén velocity in the magnetosphere and in the magnetosheath, the reconnection rate is e = 0.3, the pressure relaxation time is t sh = 3 min, the repetition time of reconnection pulses is tr = 5 min.

|
| Figure 4 |
 1/t2 (see (7)).
1/t2 (see (7)).
We still did not take into account the appearance of region 1 field-aligned currents. It is well known that a reconnection event generates field aligned currents [Pudovkin and Semenov, 1985]. As far as an FR-region moves along the current sheet (the magnetopause in our case), the contribution of this current system is included automatically in the pressure behavior near the diffusion region, but when reconnection-associated disturbances turn off from the current sheet (turn off from the magnetopause to the ionosphere in the cusp region), we have to take into account the contribution of the field-aligned current system separately.
Generally speaking, this problem is rather difficult, because we have to find a field-aligned current from each reconnection pulse, propagation of the field-aligned current in the form of an Alfvén wave from the cusp to the ionosphere, and then determine the contribution of this current system to pressure balance near the subsolar point. For the simple model under consideration, we will not attempt to solve this difficult problem but instead try to estimate the contribution of the region 1 field-aligned current system.
In our model, the FR-region propagates toward the cusp region and then
turns off to the ionosphere along a magnetic field line. The
pressure variation
P mg(1)(t) can be calculated from
equation (4) until the FR-region reaches the cusp. Our
suggestion is that the contribution of the field-aligned current
to the pressure balance at the subsolar point is constantly of the
order of
P mg(1)(t cusp), where
t cusp is the time
propagation of the FR-region from the diffusion region to the
cusp. This implies that we suppose that for each reconnection
event for
t
The result of magnetopause erosion based on this assumption
is
shown in Figure 4
(solid line). The jump-like behavior of the
magnetopause motion is the same as previously, but the average
shift is much bigger,
The model described above naturally incorporates all three
approaches to magnetopause erosion.
(1) Flux transfer
[Holzer and Slavin, 1978].
Our model is
based on the solution of the impulsive reconnection problem, which
is determined by the reconnection electric field
E*(t,y) (see (1)-(6)).
The main physical reasons for the pressure
pulse and the region 1 field-aligned current system are reconnection
events and the transfer of reconnected flux from the dayside to the
nightside of the magnetosphere.
(2) Penetration of the magnetic field from the magnetosheath
to the magnetosphere
[Kovner and Feldstein, 1973;
Pudovkin et al., 1998].
Let us rewrite pressure balance in terms of magnetic
fields. For our simple model with a symmetric current sheet, we can
suppose that the gas pressure in the magnetosheath and in the
magnetosphere is the same; hence, the pressure balance is the
following:
After each reconnection event, the second term on the right-hand
side of equation (10) is small for
t>t sh. This implies
that
magnetosheath magnetic field
effectively
penetrates
the magnetosphere at a relaxation time scale
t>t sh but
magnetospheric field does not penetrate into the magnetosheath. It
cannot be emphasized enough that no magnetic charges appear, and
the same reconnected flux is subtracted from the magnetosphere and
the magnetosheath initial flux. Penetration of magnetic field
from the magnetosheath to the magnetosphere needs to be understood
effectively as a consequence of different pressure pulse evolution
in the magnetosheath and magnetosphere as it was described
above. The bow shock and pile-up process (magnetic barrier) make
an asymmetry in pressure pulse propagation, which leads to a jump-like
motion of the magnetopause. Therefore, this effect is the essential
component of the magnetopause erosion theory.
(3) Field-aligned currents
[Maltsev and Lyatsky, 1975;
Sibeck et al., 1991].
Erosion is most often interpreted as
an effect of the region 1 Birkeland current system. It turns
out that the fringe fields of these Birkeland currents
reduce magnetic field strength near the subsolar point, and as
a consequence, the dayside magnetopause moves inward to rebuild
pressure balance.
Compared with the pressure pulse effect (or the effect of
penetration of the magnetic field from the magnetosheath to the
magnetosphere), the contribution of field-aligned currents from a
reconnection event is rather small. But it is important to note
that the effects of field-aligned currents from several
reconnection pulses are accumulated. Therefore, after each
reconnection event the magnetopause first quickly moves inward and
then reverts to a position slightly shifted to the Earth
(see Figure 4).
The difference between forward and backward motion of the
magnetopause is the effect of the region 1 Birkeland current system.
Hence, time averaged erosion mostly depends on
field-aligned currents.
1. A simple model of magnetopause erosion based on analytical
impulsive reconnection theory is presented.
2. It is shown that bursty reconnection leads to an inward jump-like
motion of the magnetopause.
3. The model incorporates all three most popular approaches:
Flux transfer, penetration of the magnetic field from
magnetosheath to magnetosphere, and the effect of a
region 1
Birkeland current system.
The first two effects are responsible
for the jump-like motion of the magnetopause, and the last one
is responsible for
the shift of the magnetopause to Earth.
Aubry, M. P., C. T. Russell, and M. G.
Kivelson, Inward motion of the magnetopause before a substorm,
J. Geophys. Res., 75, 7018, 1970.
Baker, D. N., S.-I. Akasofu, W. Baumjohann, J. W. Bieber,
D. H. Fairfield, E. J. Hones, Jr., B. Mauk, R. L. McPherron, and
T. E. Moore,
Substorms in the magnetosphere, in
Solar-Terrestrial Physics: Present and Future,
Ch. 8,
edited by D. M. Butler and
K. Papadopoulos, NASA Ref. Publ., NASA, Washington, D.C.,
1120, 1984.
Biernat, H. K., M. F. Heyn, and V. S. Semenov, Unsteady Petschek
reconnection,
J. Geophys. Res., 92, 3392, 1987.
Dungey, J., Interplanetary magnetic field and the auroral zones,
Phys. Rev. Lett., 6, 47, 1961.
Fairfield, D. H., Average and unusual locations of the Earth's
magnetopause and bow shock,
J. Geophys. Res., 76,
6700, 1971.
Galeev, A. A., M. M. Kuznetsova, and L. M.
Zelenyi, Magnetopause stability threshold for patchy reconnection,
Space Sci. Rev., 44, 1, 1986.
Heyn, M. F., and M. I. Pudovkin, A time-dependent model of magnetic field
annihilation,
J. Plasma Phys., 49, 1, 17,
1993.
Holzer, R. E., and J. A. Slavin, Magnetic flux
transfer associated with expansions and contractions of the
dayside magnetosphere, J. Geophys. Res., 84, 3831, 1978.
Kawano, H., and C. T. Russell, Survey of flux transfer events
observed with the ISEE 1 spacecraft: Dependence on the
interplanetary magnetic field,
J. Geophys. Res., 102,
11,307, 1997.
Kovner, M. S., and Ya. I. Feldstein, On solar wind interaction with
the Earth's magnetosphere,
Planet. Space Sci., 21,
1191, 1973.
Maltsev, Yu. P.,
and W. B. Lyatsky, Field aligned currents and
erosion of the dayside magnetopause,
Planet. Space Sci., 23, 1257, 1975.
McPherron, R. L., C. T. Russell, and M. P. Aubry, Satellite
studies of magnetospheric substorms on August 15, 1968,
Phenomenological model of substorms,
J. Geophys. Res., 78, 3131, 1973.
Mead, C. D., and D. B. Beard, Shape of the
geomagnetic field solar wind boundary, J. Geophys. Res., 69, 1169, 1964.
Parker, E. N., The solar flare phenomenon and the theory of
reconnection and annihilation of magnetic fields,
Astrophys. J., Suppl. Ser., 8, 177, 1963.
Petschek, H. E., Magnetic field annihilation,
NASA Spec. Publ., 50, edited by
W. N. Ness, pp. 425-439, 1964.
Petrinec, S. M., and C. T. Russell, Influencing factors on the
shape and size of the dayside magnetopause,
Adv. Space. Res., 18, 207, 1996.
Pudovkin, M. I., and A. Samsonov, Generation of pressure pulses in the
magnetosheath, in
Current topics in astrophysical and fusion plasma research, Proceedings
of the International Workshop on Plasma Physics,
edited by M. F. Heyn, W. Kernbichler, H. K. Biernat,
pp. 121-124,
Technische Univ., Graz,
1994.
Pudovkin, M. I., and V. S. Semenov, Magnetic field reconnection
theory and the solar wind magnetosphere interaction: A review,
Space Sci. Rev., 41, 1, 1985.
Pudovkin, M. I., B. P. Besser, and S. A. Zaitseva, Magnetopause
standoff distance in dependence on the magnetosheath and solar
wind parameters,
Ann. Geophys., 16, 388, 1998.
Rijnbeek, R. P., and
V. S. Semenov, Features of a Petschek-type reconnection model,
Trends in Geophys. Res., 2, 247, 1993.
Roelof, E. C., and D. G. Sibeck,
The magnetopause shape as a
bivariate function of IMF
Bz and solar wind dynamic pressure,
J. Geophys. Res., 98, 21,421, 1993.
Semenov, V. S., M. F. Heyn, and I. V. Kubyshkin, Time-dependent
field line reconnection,
Soviet. Astr. J. (in Russian), 60, 1138,
1983.
Sibeck, D. G., Signatures of flux erosion from the dayside
magnetosphere,
J. Geophys. Res., 99, 8513, 1994.
Sibeck, D. J., R. E. Lopez, and E. C. Roelof,
Solar wind control of the magnetopause shape, location, and
motion, J. Geophys. Res., 96, 5489, 1991.
Shue, J.-H., J. K. Chao, H. C. Fu, C. T. Russell, P. Song,
K. K. Khurana, and H. J. Singer, A new functional form to study solar
wind control of the magnetopause size and shape,
J. Geophys. Res., 102, 9497, 1997.
Shue, J.-H., et al.,
Magnetopause location under extreme solar
wind conditions,
J. Geophys. Res., 103, 17,691, 1998.
Sweet, P. A., The neutral point theory of solar flares, in
Electromagnetic Phenomena in Cosmic Physics, edited by B. Lehnert,
pp. 123-129, Cambridge Univ. Press, New York, 1958.
Tsyganenko, N. A., and D. J. Sibeck,
Concerning flux erosion from the dayside magnetosphere, J. Geophys. Res., 99,
13,425, 1994.
 1 RE. Therefore, the
details (jumps)
of magnetopause motion are determined by bursty reconnection, but
erosion itself mostly depends on the strength of the region 1
field-aligned current system.
1 RE. Therefore, the
details (jumps)
of magnetopause motion are determined by bursty reconnection, but
erosion itself mostly depends on the strength of the region 1
field-aligned current system.
4. Discussion
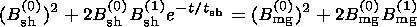
(10) 5. Conclusions
Acknowledgments
Part of the work was done while V.S.S. and N.V.E. were at the Space
Research Institute of the Austrian Academy of Sciences in Graz, and while H.K.B.
and S.M. were at the Institute of Physics of the State University of St. Petersburg.
This work is partially supported by INTAS-ESA project 99-01277, by the INTERGEOPHYSICS
programme of the Russian Ministry of Higher Education, by the Austrian "Fonds zur
Förderung der wissenschaftlichen Forschung''
under project P13804-TPH, by grant No. 98-05-65290 of the Russian Foundation
of Basic Research, by grant No. 97-0-13.0-71 of the Russian Ministry of Education,
and by the Austrian Academy of Sciences "Verwaltungstelle für Auslandsbeziehungen."
References
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on December 6, 2002.