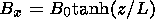
A. V. Runov and M. I. Pudovkin
St. Petersburg State University, St. Petersburg, Russia
Bruno P. Besser
Space Research Institute, Austrian Academy of Sciences, Graz, Austria
As is now known, the most powerful space plasma processes occur in the vicinity of relatively small-scale regions, which, following Alfvén, may be called "active regions" [Alfvén, 1981]. They may be force-free structures in the solar atmosphere, pinch configurations, or plasma sheets. In any case, the active region is a conditionally stable plasma-magnetic field configuration. The main characteristic feature of objects of such kind is the ability to accumulate magnetic energy as long as the stability conditions are valid. As soon as the stability conditions are violated, the plasma-magnetic field configuration system loses its stability, and the accumulated energy may be released.
This scenario seems to be realized during solar flares and magnetospheric substorms. In the latter case, the magnetotail plasma sheet plays the role of the active region, which is able to accumulate magnetic field energy. The source of the energy may be the solar wind-magnetospheric interaction. This interaction has a complex character and may include the day-side reconnection process as well as quasi-viscous interaction at the magnetopause, and hydrodynamic instabilities that may develop in the solar wind plasma passing by the magnetosphere. All of the processes included produce an electric field in the vicinity of and at the magnetopause. This electric field may locally constrict the plasma sheet of the magnetotail, which is followed by current density enhancement in the sheet, or, similarly, by magnetic energy accumulation. But the increase of the current density or the total pressure gradient may lead to the development of current- or gradient-driven plasma instabilities in the compressed plasma sheet, and to its destruction and subsequent release of the accumulated energy. The first phase of this draft sketch -- the phase of energy storage -- may be associated with the preliminary or growth phase of the magnetospheric substorm, and the second phase with the substorms' onset.
The scenario roughly prescribed below may correspond to a driven-in or forced magnetic field reconnection process. Driven magnetic reconnection was a subject of many studies. This process was investigated in detail in a set of papers by T. Hayashi and T. Sato [Hayashi and Sato, 1978; Sato, 1979; Sato and Hayashi, 1979] and M. Hoshino [Hoshino, 1991]. In all of these papers, the results of MHD numerical simulations are discussed. In the series of T. Hayashi and T. Sato papers, the strong or fast reconnection process model is analyzed. This process is initialized by the plasma and total energy inflow given at the inflow boundary. The initial configuration in this case is not a plasma sheet, but a current sheet with a uniform plasma density distribution. The magnetic field pressure is balanced by a plasma pressure gradient produced by a non-uniform plasma temperature. The density of the inflow plasma is two times the uniform background density. This fast moving flux of dense plasma converges symmetrically to the neutral line and compresses the current sheet. As a result, the temperature (pressure) grows about ten times in the compressed current sheet. The electrical resistivity of the plasma is supposed to be dependent on the current density excess over a given critical value. The intensification of the current sheet followed by resistivity growth results in magnetic field reconnection, high plasma acceleration along the current sheet, and slow-mode shock formation. At a quasi steady-state stage, this process is quite similar to Petschek's model prediction [Petschek, 1964].
In contrast, M. Hoshino had considered a slow process. The initial state in his model is the isothermic Harris-type plasma sheet, and the disturbance is given by a small amplitude plasma velocity variation. In this case, there is no dense plasma injection into the plasma sheet, the plasma density increases at the neutral line of the sheet, and it decreases near the inflow boundary -- the situation is quite contrary to the Hayashi and Sato model. The electrical resistivity of the plasma is supposed to depend on the magnetic pressure gradient which is a model representation of the low hybrid drift-type (LHD) plasma instability. In the Hoshino model, the resistivity plays a key role. After a long period of plasma sheet compression, the current density at the neutral line of the plasma sheet increases about 10 times. A maximum value of the resistivity normalized to its background value in the vicinity of the neutral line is about 0.0005. So, the inductive electric field in this case is not more than 0.005 normalized units. In Hoshino's model of weak magnetic reconnection, the plasma outflow velocity is about 0.15-0.2 va. The resulting magnetic field topology and plasma convection are interpreted as the tearing-mode instability result.
Concerning the plasma sheet in the Earth's magnetotail, Hoshino's model is more preferable. But the substorm onset is a more dynamical process than the process of weak reconnection described by this model.
In both models of strong [Sato and Hayashi, 1979] and weak [Hoshino, 1991] forced reconnection, only a late stage of the process is studied. In particular, the phase of energy storage in the plasma (current) sheet is not investigated.
As was mentioned in the paper by Sato and Hayashi [1979], the process of driven magnetic field reconnection is preceded by a rather long period of magnetic energy accumulation associated with plasma (current) sheet thinning. This process is shown to stop at the moment the current density within the central part of the plasma sheet reaches a critical value corresponding to the development of the hypothetical plasma instability (most probably of LHD or ion-cyclotron type). From the moment of plasma instability development followed by resistivity growth, the reconnection phase of the process is beginning.
In our work, a part of which is presented in this paper, a set of computer experiments was carried out to investigate all phases of the process in detail. At the first part of this set of simulations, the evolution of the simplest plasma sheet configuration, known as the Harris sheet or a flat pinch, used also in the Hoshino [1991] model, in the presence of a non-uniform external electric field is modeled. We analyze the fast (strong) regime as well as the slow one. The following question should be answered:
The analysis is based on a numerical solution of the one-fluid nonideal MHD equations. This paper is devoted mainly to the detailed investigation of the first phase of the process: fast wave-plasma sheet interactions.
The simplest current-carrying plasma sheet description known as the "Harris sheet" or "flat pinch" is used as the initial equilibrium state:
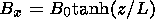 |
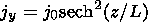 | (1) |
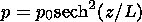 |
where
Bx is the
x component of the magnetic field,
Bz=By=0,
jy is the current density,
j0=B0/m0
L,
p is the plasma pressure,
p0=B02/2m0,
L is the
characteristic length of the sheet. The
x and
z coordinates are directed
along and across the sheet, correspondingly. It is assumed that
there is no dependence of physical values on
y, so
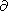 /
/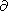 y=0.
Besides, an unlimited extension of the layer in
the
x direction is assumed.
y=0.
Besides, an unlimited extension of the layer in
the
x direction is assumed.
The initial steady-state sheet (1) is disturbed by an externally given electric field that has only a y component in the same direction as the electric current in the plasma sheet. The external electric field is given at the inflow boundary as
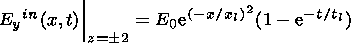 | (2) |
where E0 is the given value, which is small compared to the Alfvénic electric field Ea=va Bx0, xl is the scale of the disturbance in the x direction, and tl is the disturbance growth time introduced into the model to avoid numerical instabilities. This external electric field gives rise to plasma convection, according to Ohm's law
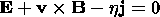 | (3) |
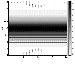
|
| Figure 1 |
It should be noted that this model of the initial disturbance as well as the initial state model essentially differs from the model of the initial state and disturbance used by Sato and Hayashi [1979], Sato [1979]. The dense plasma inflow is not supposed in our model, in contrast to the Sato and Hayashi [1979] model, and we use the isothermal Harris-type plasma sheet, like Hoshino [1991], as the initial condition (see Section 1). In our opinion, the model with a plasma sheet and a given external electric field at the boundary as a disturbance is more adequate for the magnetotail situation.
It is presumed that the plasma sheet evolution caused by the disturbance (2) may be described in the MHD approach. The MHD approach is valid if the characteristic scale of the gradients of physical quantities is not less than about 10 Larmor radii. In this case, the plasma sheet evolution is characterized by the following set of equations of one-fluid, nonideal isotropic compressible MHD [Hayashi and Sato, 1978; Scholer et al., 1990]:
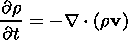 | (4) |
 | (5) |
 | (6) |
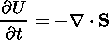 | (7) |
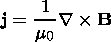 | (8) |
 | (9) |
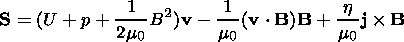 | (10) |
where the magnetic field B is normalized by the value B0, r is the mass density, v is the plasma velocity, normalized by r0=(g/Cs20) p0, where Cs0=(gp0/r0)1/2, and va=Bx0(m0r0)-1/2; h is the electrical resistivity, normalized by h0=m0 L va, and the time is normalized by the Alfvén transport time ta=L/va. g is the polytropic exponent, I is the unit tensor, and combination aa denotes a diad.
It is assumed, following Sato and Hayashi [1979] and Scholer and Roth [1987], that plasma electrical resistivity is a threshold-like function of the electric current density:
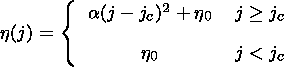 | (11) |
where a is a coefficient that defines the magnitude of the resistivity, jc is some critical value of the current density, h0 is the uniform background resistivity.
As the initial state and the disturbance are symmetric with
respect to both the
x=0 and
z=0 axes, the MHD equation
system (3-6) is solved numerically in a rectangular box of
104  104 meshpoints, which corresponds to the
upper right
quadrant
(x>0, z>0). Besides, the physical computation region
x=[0,10],
z=[0,2] corresponds to a numerical box of
100
104 meshpoints, which corresponds to the
upper right
quadrant
(x>0, z>0). Besides, the physical computation region
x=[0,10],
z=[0,2] corresponds to a numerical box of
100  100 points, so the mesh size along the
x axis equals
Dx=0.1 and the mesh size along the
z axis equals
Dz=0.02;
additional points in both directions are used to construct the
boundary conditions. It should be emphasized that the mesh size
along the
x axis,
Dx, is very large, so the numerical
resistivity is rather high. However, as we analyze the initial phase
of the process (fast wave-plasma sheet interaction), which is
not connected to shock-wave generation, the smoothing of
plasma parameter gradients associated with the relatively high
numerical resistivity is not essential in this case.
This value of
Dx is used to minimize the run time of the
computation. For the analysis of the
latest stage of the process connected with magnetic reconnection and
slow shock fronts generation, a more dense grid is used.
100 points, so the mesh size along the
x axis equals
Dx=0.1 and the mesh size along the
z axis equals
Dz=0.02;
additional points in both directions are used to construct the
boundary conditions. It should be emphasized that the mesh size
along the
x axis,
Dx, is very large, so the numerical
resistivity is rather high. However, as we analyze the initial phase
of the process (fast wave-plasma sheet interaction), which is
not connected to shock-wave generation, the smoothing of
plasma parameter gradients associated with the relatively high
numerical resistivity is not essential in this case.
This value of
Dx is used to minimize the run time of the
computation. For the analysis of the
latest stage of the process connected with magnetic reconnection and
slow shock fronts generation, a more dense grid is used.
The boundary conditions are specified for three types of boundaries: the inflow boundary ( z=2.0 ), the free outflow boundary ( x=10.0 ), and two symmetry/antisymmetry boundaries ( x=0.0 and z=0.0 ). The specifications are summarized in Table 1; extrapol. denotes fb+1=fb, where the subscript b denotes the point at the physical boundary, and f corresponds to the value to be computed, and symm./asymm. denote fb+1=fb-1 and fb+1=-fb-1, correspondingly.
The two-step Lax-Wendroff (LW) numerical scheme is used. A time step of the numerical procedure is determined by the Courant-Friedrichs-Levi stability criterion.
As follows from the previous section, the model has the following set of free parameters: polytropic exponent g, initial value of the sound velocity Cs0, the disturbance magnitude v0, scale xl and growth time tl, the current dependent resistivity coefficient a, and the critical value of the current density jcr. Because a two-dimensional model is considered, the value of g is taken to be 2 [Sato and Hayashi, 1979]. The value of Cs0 is chosen equal to (2)1/2, so the effective temperature T=p/r at t=0 equals 1. Other parameters are varied in the set of calculations. The results, discussed below are obtained with v0=0.05, xl= a=0.1, jcr=2.50.

|
| Figure 2 |
The positive variation of the current density has its maximum at the front of the wave. Thus, the front of the fast magnetosonic wave is the front of a "switch-on" wave.
It is interesting to note that the configuration of the disturbance profile changes upon moving to the sheet. Indeed, as is seen in the figure, the velocity of the back front of the disturbance is higher than that of the leading front. And as a result, the width of the disturbance along the z axis decreases with time, so that in the vicinity of the current sheet, the extension of the disturbance along the z axis proves to be about Dz=(0.3-0.4)L.

|
| Figure 3 |
|
| Figure 4 |
The two-dimensional distribution of the electric field in the motionless frame of reference at time instances t=0.50, 1.00, 1.50, and 2.00 of the normalized time is displayed in Figure 3. The electric field, expanding from the inflow boundary inward as the fast-wave front, switches on the plasma convection. The plasma velocity vector distributions at the same moments are shown in Figure 4.
At this point, it must be noted that though the plasma convection front moves at the fast magnetosonic wave speed, the plasma behind it is moving with the electric drift velocity, which is much less than the wave front velocity.
The calculations show that the fast magnetosonic wave is reflected
from the plasma sheet neutral plane after the front reaches it
and moves backward to the inflow boundary. Then, as the electric
field is supposed to be constant in time at the inflow boundary,
the wave front is reflected from the boundary and moves toward the
neutral line again. This process has a well pronounced
quasi-recurrent character. It should be noted that the change of
front motion direction, described below, is not followed by
the change of electric field and, correspondingly, plasma
convection direction. For the entire period under consideration,
the plasma generally flows toward the neutral line. However, the
reflection of the disturbance from the current sheet is
essentially "inelastic," that is, the interaction of the
disturbance with the sheet results in a noticeable change of the
parameters of the latter. In particular, the current intensity,
plasma density and pressure increase by the values of
Dj=0.003 ,
Dr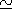 0.03, and
Dp=0.005,
correspondingly. As a result, after a series of wave bounces,
the magnetic energy of the system essentially increases. Besides,
as may be seen in the graphics presented in Figure 4, a
remarkable
x component of the plasma velocity appears. At
t=2.0, the plasma flow shows a vortex character. The vortices of
plasma convection at
x=
0.03, and
Dp=0.005,
correspondingly. As a result, after a series of wave bounces,
the magnetic energy of the system essentially increases. Besides,
as may be seen in the graphics presented in Figure 4, a
remarkable
x component of the plasma velocity appears. At
t=2.0, the plasma flow shows a vortex character. The vortices of
plasma convection at
x= 2.5 -
2.5 -  5.0 are associated with
regions of the negative electric field (Figure 3).
5.0 are associated with
regions of the negative electric field (Figure 3).

|
| Figure 5 |
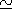 4.0. After that moment, the
magnetic energy increase stops, and the process approaches
and proceeds in a steady-state regime
(analogy of the stationary convection in the
magnetotail plasma sheet), and the plasma convection exhibits a
quasi-hyperbolic character. Taking into account that energy
continues to enter the system, one may suppose that the energy
input is balanced by an increased output rate during this period. The
physical mechanism of the increase of the energy output rate may
be understood from the data presented in Figure 5, where graphics
of time variations of the current density (upper panel),
current-dependent resistivity, the electric field, and
the plasma pressure
at the point
x=0, z=0 are presented. As is seen from the
presented data, the current density at the axis of the sheet grows
in a step-like manner until
t
4.0. After that moment, the
magnetic energy increase stops, and the process approaches
and proceeds in a steady-state regime
(analogy of the stationary convection in the
magnetotail plasma sheet), and the plasma convection exhibits a
quasi-hyperbolic character. Taking into account that energy
continues to enter the system, one may suppose that the energy
input is balanced by an increased output rate during this period. The
physical mechanism of the increase of the energy output rate may
be understood from the data presented in Figure 5, where graphics
of time variations of the current density (upper panel),
current-dependent resistivity, the electric field, and
the plasma pressure
at the point
x=0, z=0 are presented. As is seen from the
presented data, the current density at the axis of the sheet grows
in a step-like manner until
t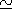 4.5, and at
t
4.5, and at
t 3 the
current density in the region of maximal compression of the sheet
reaches and then exceeds the critical value
jcr=2.50.
According to the model, this has to result in a burst-like increase of
the plasma resistivity and intensification of the magnetic field
reconnection process.
In accordance with equation (11),
the "anomalous" resistivity
h develops at
t
3 the
current density in the region of maximal compression of the sheet
reaches and then exceeds the critical value
jcr=2.50.
According to the model, this has to result in a burst-like increase of
the plasma resistivity and intensification of the magnetic field
reconnection process.
In accordance with equation (11),
the "anomalous" resistivity
h develops at
t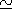 4, when the current density approaches
the threshold value
jcr, then the resistivity significantly grows with a peak
at
t
4, when the current density approaches
the threshold value
jcr, then the resistivity significantly grows with a peak
at
t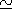 4.5. It is interesting to note that
in spite of a rapid
increase of plasma resistivity, the current density also
increases at that time, which supposes a corresponding increase of
electric field intensity. And indeed, as may be seen from
the
results
presented, the time variation of the electric field at
the vicinity of the point (0,0) is completely determined by the
time behavior of the current-dependent resistivity. In particular,
a jump of
h at
t=4 results in a corresponding jump of the
E field. And though the
E field intensity at this point is
much lower than
E0 at the inflow boundary, it is sufficient to
provide the necessary increase of the plasma and energy outflow.
Further variations of the resistivity and the electric field in
the region of maximal compression of the plasma sheet are
characterized by a set of quasi-recurrent activations with
decreasing amplitude.
4.5. It is interesting to note that
in spite of a rapid
increase of plasma resistivity, the current density also
increases at that time, which supposes a corresponding increase of
electric field intensity. And indeed, as may be seen from
the
results
presented, the time variation of the electric field at
the vicinity of the point (0,0) is completely determined by the
time behavior of the current-dependent resistivity. In particular,
a jump of
h at
t=4 results in a corresponding jump of the
E field. And though the
E field intensity at this point is
much lower than
E0 at the inflow boundary, it is sufficient to
provide the necessary increase of the plasma and energy outflow.
Further variations of the resistivity and the electric field in
the region of maximal compression of the plasma sheet are
characterized by a set of quasi-recurrent activations with
decreasing amplitude.
The plasma pressure also grows significantly during the period
0
The other circumstance leading to this situation is a rather small
scale of the external electric field in the
x direction,
which results in a correspondingly extensive stretching of the compressed
current layer in the
x direction.
As follows from the results presented above, the external
electric field given at the inflow boundary propagates through
the plasma sheet as the fast magnetosonic wave. The front of that
wave switches on plasma convection and the Poynting vector flux
and thereby provides the energy input into the current sheet. A
very interesting feature of the electric field penetration into
the plasma sheet is repeated reflection of the wave front from the
current sheet and the inflow boundary. Every act of the
front
reflection from the current sheet manifests itself in a pulse of
the electric field intensity, current density, and plasma pressure
jump at the neutral line of the sheet. It seems tempting to
suppose that repeated intensifications of equatorward-moving
auroral arcs observed during the preliminary phase of substorms
may be associated with an analogous process within the
magnetospheric plasma sheet.
At the same time, the reflections of the wave front from the
current sheet are not associated with the change of the sign of the
electric field.
Correspondingly, the Poynting vector
provides a continuous energy input into the current sheet and the
increase of the current intensity up to the values exceeding the
plasma stability threshold value. This, in turn, results in the
development of the anomalous resistivity, formation of a magnetic
X line, and onset of the magnetic reconnection process. All these
features of the process developing during the initial phase of the
plasma sheet evolution seem to be peculiarly independent of the
geometrical characteristics of the current sheet and the electric field
intensity
E0.
However, the intensity and properties of the subsequent
reconnection process in the case under consideration are rather special:
as is seen in Figure 5, the maximum value of the electric
field within the current sheet is about
2.5
All these peculiarities of the magnetic reconnection in the
model
discussed
may be explained by two factors.
As was stated above, a relatively high numerical resistivity of the
plasma results in a correspondingly low jump of
resistivity described by equation (11).
This, in turn, results in a rather small variation of the current
density and magnetic field intensity, in particular, in a small
z component of the magnetic field in the reconnection region.
Then, in the expression for the
y component of the electric
field within the current sheet
E=hj + vx
Bz, the last term
on the right-hand side may be neglected, and the electric field
variation is described mainly, in accordance with Figure 5, by the first
term:
E=hj. Thus, the magnetic field reconnection
in the
current sheet with the chosen input parameters corresponds on the
whole to the Sweet-Parker model rather than to the Petschek model.
At the same time, the
solution
obtained
allows one to formulate the
conditions favorable for a model of fast Petschek-type
reconnection. First of all, it is necessary to decrease the
numerical resistivity. Besides, it would be necessary to decrease
the value of the ratio
zb/L, which will result in a more narrow
localization of the region of fast wave interaction with the
current sheet, and, correspondingly, in a smaller scale of the
diffusion region.
Results of the calculations will be presented in a subsequent
paper.
Alfvén, H.,
Cosmic Plasma,
D. Reidel Publishing Company, Dordrecht, Holland, 1981.
Hayashi, T., and T. Sato,
Magnetic reconnection: Acceleration, heating and shock formation,
J. Geophys. Res., 83, 217, 1978.
Hoshino, M., Forced magnetic reconnection in a plasma sheet
with localized resistivity profile excited by lower hybrid drift type
instability,
J. Geophys. Res., 96, 11,555, 1991.
Petschek, H. E., Magnetic field annihilation, in
Proceedings of the AAS-NASA Symposium on Physics of Solar Flares, NASA Spec.
Publ., 50, 425,
1964.
Sato, T., Strong plasma acceleration by slow shocks resulting from
magnetic reconnection,
J. Geophys. Res., 84, 7177, 1979.
Sato, T., and T. Hayashi, Externally driven magnetic reconnection and
a powerful magnetic energy convertor,
Phys. Fluids, 22, 1189, 1979.
Scholer, M., and D. Roth,
A simulation study on reconnection and small-scale plasmoid
formation,
J. Geophys. Res., 92, 3223, 1987.
Scholer, M., T. Terasawa, and F. Jamitzky,
Reconnection and fluctuations in compressible MHD: A comparison of
different numerical methods,
Comput. Phys. Commun., 59, 175, 1990.
The magnetic field configuration, plasma convection,
current density, and plasma pressure
at
t=10.0 are shown in Figure 6. As is seen in the figure, the
reconfiguration of the plasma flow associated with the
propagation of the external electric field into the plasma sheet
results in the formation of a quasi-hyperbolic plasma flow all over the
system under consideration without any shock wave appearance. At
the same time, the magnetic field line structure is characterized
by the existence of a neutral line of
X type, which may be
considered as obvious evidence for magnetic field
reconnection development. On the whole, the magnetic field-plasma
convection system corresponds to that in the Sweet-Parker
problem rather than that of the Petschek model. This situation seems to
be associated first of all with a rather large numerical viscosity
of the calculation scheme that results in a relatively small
increase of the current-driven
plasma resistivity (by about an order of
magnitude).

Figure 6
4. Discussion and Conclusions
 10-3Ea.
Besides, the reconnection process is not associated with the
formation of any shock waves. And, finally, the reconnection
process is not followed by any visible decrease of the accumulated
magnetic energy.
10-3Ea.
Besides, the reconnection process is not associated with the
formation of any shock waves. And, finally, the reconnection
process is not followed by any visible decrease of the accumulated
magnetic energy.
Acknowledgments
This work was supported by the Russian Foundation for Basic Research,
grants No. 99-05-04006 and No. 00-05-64894.
References
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on December 6, 2002.