International Journal of Geomagnetism and Aeronomy
Vol. 3, No. 1, January 2002
Substorm study based on the Paraboloid model of the magnetosphere
I. I. Alexeev and S. Yu. Bobrovnikov
Institute of Nuclear Physics, Moscow State University,
Moscow, Russia
Received 14 August 2001, published online 24 January 2002
Contents
Abstract
A substorm is widely accepted to be a global phenomenon in
magnetospheric physics. It is a large-scale process consisting of
coherent phenomena. It is very interesting to study individual phenomena
such as reconnection during the
onset of a
substorm
flows in the tail,
ionospheric precipitation, particle injection, etc.
However, we would like to emphasize that it is important to investigate
the substorm as a unified process depending on the conditions in the solar
wind and within the magnetosphere. For this purpose we should use a global
magnetospheric model. In this case it is the Paraboloid model. It is important
to note that the Paraboloid model comprises all the necessary sources
of the magnetic field in the magnetosphere which can be distinguished
from each other. This enables calculation of the magnetic field of
different sources with different timescales. By using this model,
we can
also calculate global characteristics of the magnetosphere, such as the
magnetic fluxes in the polar cap and in the auroral oval as a function
of model parameters depending on time and
solar wind conditions. This makes it possible to find the criteria of
magnetosphere transformation into the metastable configuration, when
development of a substorm becomes inevitable.
Using these criteria, constrains were found which should be imposed on
the model parameters to determine the substorm onset.
The results obtained make it feasible to explain the external
substorm triggering by the northward turning of the
interplanetary magnetic field
in the solar wind.
A case study of the 10 January 1997,
substorm event confirms
our findings.
Introduction
Substorms are currently known as global phenomena consisting
of a coherent set of processes within the magnetosphere, ionosphere, and the
interplanetary medium. Magnetospheric dynamics during substorms consists of
a sequence of energy loading and dissipation events accompanied by
well-known observational phenomena such as cross-tail current and polar cap
magnetic flux enhancement, field line stretching with subsequent dipolarization,
Joule heating in the ionosphere,
auroral particle precipitation, ring current enhancement, and plasmoid
formation
[ Baker et al., 1996].
These observations support the idea that a substorm is
a global configurational instability of the magnetosphere
[ Baker et al., 1999;
Sitnov et al., 2000].
On the
basis of
viewpoint, it is important to answer certain questions.
Can one apply a global model of the magnetospheric magnetic field to the
substorm investigation? If one can, what are the main features of this model?
In our study we used the Paraboloid model of the magnetosphere, and in
this paper we try to explain why it can be used for the consideration of
substorms triggered by the
interplanetary magnetic field
(IMF) northward turning.
Substorm triggering by the IMF northward turning is a very interesting
and contradictory field of substorm physics.
This problem has been studied since 1975.
Caan et al. [1975]
performed a statistical analysis of a large set of
substorms and have shown that the onset begins at a time when the
IMF
Bz changes from a negative value to zero, after a long
period of being
directed southward.
Rostoker et al. [1982]
found a distinct relation between
IMF northward turnings and substorm onsets for a number of intense substorms.
Later,
Rostoker [1983]
found more evidence for this phenomenon.
He showed that
Bz remained negative for a period of ~2 hours
for the storm on 20 January 1978, and
 1 hour for the storm on August
19, 1978.
Lyons [1995]
noted that sudden changes in the IMF
By could also control the substorm onset.
Troshichev et al. [1986] showed
that a decrease of
|By| down to zero can trigger substorm onset.
McPherron et al. [1986]
studied the IMF
Bz at the time of onsets and showed that 44% of 126 events
were directly
related to the IMF northward turning,
and 29% of events occurred at a steady negative
Bz.
Taking into account changes in the IMF
By investigated by McPherron,
Lyons [1996]
revealed a distinct relation between sudden IMF
changes and substorm onsets.
Lyons [1995]
proposed a substorm model
that explains the IMF triggering of a substorm expansion by a
decrease of the electric
field in the near-Earth magnetotail and, as a consequence, development of
field-aligned currents.
Nishida [1997]
carried out recently a case study
and found no evidence for the Lyons theory. They have found an
increase of the electric field just before substorm expansion,
a fact contradicting
the Lyons
theory. Thus there is no commonly accepted theory of the mechanism
that connects changes in the IMF to a substorm expansion onset.
1 hour for the storm on August
19, 1978.
Lyons [1995]
noted that sudden changes in the IMF
By could also control the substorm onset.
Troshichev et al. [1986] showed
that a decrease of
|By| down to zero can trigger substorm onset.
McPherron et al. [1986]
studied the IMF
Bz at the time of onsets and showed that 44% of 126 events
were directly
related to the IMF northward turning,
and 29% of events occurred at a steady negative
Bz.
Taking into account changes in the IMF
By investigated by McPherron,
Lyons [1996]
revealed a distinct relation between sudden IMF
changes and substorm onsets.
Lyons [1995]
proposed a substorm model
that explains the IMF triggering of a substorm expansion by a
decrease of the electric
field in the near-Earth magnetotail and, as a consequence, development of
field-aligned currents.
Nishida [1997]
carried out recently a case study
and found no evidence for the Lyons theory. They have found an
increase of the electric field just before substorm expansion,
a fact contradicting
the Lyons
theory. Thus there is no commonly accepted theory of the mechanism
that connects changes in the IMF to a substorm expansion onset.
In this paper we would like to answer two questions:
(1) Can we use the global magnetospheric model to study substorms,
and how can
this be done? (2) What is a possible
mechanism of substorm triggering by the IMF northward turning?
As a case study, we will focus on the substorm of 10 January 1997.
The Model
Let us define the features of the model of the magnetospheric magnetic field
used to study the substorm.
First, we should consider the time constraints. The characteristic times
of different current systems in the magnetosphere are in the range from
minutes (as Region 1 field-aligned currents) to tens of minutes
(tail current
system) and to hours (ring currents). Thus the first feature of the model should
be its ability to operate with a
time scale of a
few minutes. We cannot
use a timescale with steps less than a few minutes because the model of the
magnetospheric magnetic field does not take into account wave processes.
A level of disturbances in the magnetosphere, which can be estimated by the
Dst or
Kp indices, can change rather strongly. Fluctuations
in the magnetic field have to be either of the same order or exceed the mean value.
Thus
the second feature of the model should be its ability to provide reasonable
calculation results at any level of a disturbance. This means that
the calculated magnetic field in each region of the magnetosphere should
not contradict observations and physical sense. On the other hand,
the appearance
of such contradictions should correspond to some active magnetospheric
phenomena (as substorm onset) and be accepted as a limit of the
model application. This feature should be accompanied by the following:
a continuous dependence on the input data. In other words, small differences
in the input data (measurements, indices, etc.) should lead to relatively small
differences in the calculated magnetic field at the point of interest. This
is an important feature that
can only be satisfied when the parameters of the
model have continuous functional dependencies on the input data and time.
The time-dependent calculation demands that the model parameters
follow a time-dependent behavior
of different current systems. Thus the next feature is a reasonable
set of model parameters. It is also important for the model to make possible
using different calculation schemes to obtain the best results for
the case study. Different calculation schemes can be used for different
sets of input data. Thus the model of the magnetic field should not
depend directly on the input data (measurements).
The model that
satisfies all these requirements is the Paraboloid model
of the magnetosphere which has been developed by I. I. Alexeev and is
maintained by
a group of researchers from the Skobeltsyn Institute of Nuclear Physics of
the Moscow State University
[Alexeev, 1987;
Alexeev and Bobrovnikov, 1997, 1999].
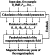
|
|
Figure 1
|
The magnetic field calculation using the Paraboloid model
is presented in
Figure 1.
It is important
to note that this is a two-step
scheme. The first one is the calculation of the
model parameters. At this step, some empirical ideas or models
("submodels")
can be used to find the parameters. However, the Paraboloid model can be used
at this step for the iteration process ("Feedback'' arrow in
Figure 1)
to obtain the best results. It is one of the most important
parts of any calculation
scheme. It allows us to satisfy the important conditions
that cannot be obtained
with an appropriate accuracy from empirical "submodels." The
second step is a calculation of the magnetic field anywhere
in the magnetosphere.
An example of the calculation using this
scheme is presented below.
Substorm Onset in the Model
Substorm onset is the most important feature of substorms.
Thus the model we are going to use
should represent the substorm onset in terms
of its parameters. Let us consider
three principal parameters of the Paraboloid
model: the distance to the subsolar point
R1, the distance to the
earthward edge of the tail current sheet
R2, and the magnetic flux
in the polar cap
F PC. There are also three sources
of the
magnetospheric
magnetic field: the dipole, the magnetopause currents screening the dipole,
and the tail current system consisting of the cross-tail current and
magnetopause screening (and closure) currents. Playing with these
parameters of the magnetic field, we found that at appropriate values
of these parameters a point with
Bz=0 appears at the inner edge
of the tail current sheet. This can be associated with neutral line formation
in the plasma sheet at the onset time. However, the question that remains
to be
answered is: Does it really have physical meaning?
The neutral point appears at relatively high values of the magnetic flux in
the polar cap (in the tail lobe). This high value of
F PC corresponds
to the enhanced cross-tail current observed during substorms. Thus
the neutral point in the Paraboloid model is formed when the cross-tail current
is highly enhanced, the situation being very similar to the substorm onset conditions.
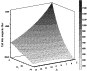
|
|
Figure 2
|
|
|
Figure 3
|
The Paraboloid model enables calculation of all possible values
of the
model parameters corresponding to the neutral point formation. The
results obtained are presented in
Figure 2.
It can be seen
that the critical value of
F PC increases strongly when the
distances
to the subsolar point and to the inner edge of the tail current sheet decrease
and vice versa. It is important to note that taking into account the ring current
and Region 1
field-aligned current slightly changes the results of the
calculations.
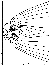
On the basis of
Figure 3,
which shows the field lines in
the Paraboloid
model at the noon-midnight meridian, we define three magnetospheric
domains and their magnetic fluxes.
1.
F head is the magnetic flux in the
inner magnetosphere.
2.
F lobe is the magnetic flux in the
tail lobe (at the infinity)
equal to the polar cap magnetic flux ( F PC ).
3.
F PS is the magnetic flux through
the plasma sheet
(from the inner edge of the current sheet up to infinity),
forming the auroral oval.
Therefore the main condition for the stability of the magnetosphere is
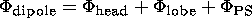 | (1) |
F dipole is the total magnetospheric
magnetic flux
which is equal to the magnetic flux of the Earth's dipole.
Formation of the neutral point
violates this equation. At this time,
F PS becomes different from
the auroral oval magnetic flux,
and
F lobe becomes different from
the polar cap magnetic flux. The polar cap and auroral oval magnetic fluxes
decrease abruptly and the magnetic flux in the inner magnetosphere increases
(dipolarization). This is the process that goes on after the expansion
of a substorm. We believe that we defined the substorm onset
conditions in terms of the model parameters.
The location
of
the neutral point
remains to be mentioned.
In our model
the neutral point
appears at the inner edge of the tail current sheet close to
the magnetopause, and one can say that it is not a proper place for a
substorm onset initiation. As mentioned above, "contradictions
to the observations should correspond to some of the active magnetospheric
phenomena and should be considered as a limit for the model application";
that is, formation of the neutral point corresponds to the limit of the
model applicability. The results of the calculations performed after this
limit time
cannot be treated as reliable.
Indeed, for our study it is most important that the
Bz component of
the magnetic field becomes zero somewhere in the magnetosphere as the
cross-tail
current increases.
It corresponds to the conditions when an additional magnetic
flux is needed to transform the magnetospheric configuration. This is what we
call global instability of the magnetosphere. The neutral point formation
is considered as an incapability of the magnetosphere to redistribute the magnetic
flux according to new external or internal conditions.
Equation (1)
yields that an increase of the magnetic
flux in one of the defined domains leads to a decrease of the fluxes in the other
domains.
After the IMF turns northward,
the inner magnetospheric domain grows, and
F head increases. At the same time,
the tail lobe magnetic flux
F lobe does not change.
In fact, this process must be accompanied by a decrease of the magnetic flux
in the plasma sheet. If this decrease is larger than the initial
F PS, the neutral line should appear.
Thus the final statement of this section is that the above considerations
are model independent: only real values of the magnetic fluxes depend on
particular model.
Scenario of a Substorm
Now we would like to propose a possible scenario for substorms
triggered by the IMF northward turning. This kind of substorm is chosen
it has the most obvious influence on the model parameters.
Again,
let us consider
three parameters of the model:
R1,
R2,
and
F lobe.
During the growth phase of the substorm the standoff
distance decreases, the magnetopause shifting earthward.
The subsolar distance and the magnetopause form were found as functions of
solar wind parameters by
Shue et al. [1997].
It has been noted that this distance depended on
the IMF
Bz component, decreasing when the IMF
Bz becomes
negative. We think this phenomenon may have two explanations.
The first cause: when the IMF turns southward the intensity of the field-aligned
currents increases significantly. They give a negative contribution
of about 10 nT to the magnetic field in the dayside magnetosphere
[Alexeev et al., 1997;
Tsyganenko and Sibeck, 1994].
The other cause is an increase of the cross-tail current.
Its contribution to the dayside magnetosphere is of
the same order as that of the field-aligned currents
[Alexeev and Bobrovnikov, 1997;
Alexeev et al., 1997].
The magnetic pressure at the subsolar
point decreases with the enhancement of
the field-aligned or tail currents.
This is followed by a decrease of the standoff distance.
Other parameters changing during substorms are the distance to the inner
edge of the tail current sheet and the magnetic flux in the tail lobe.
It is also well known that during the substorm growth phase the magnetic flux
increases and the tail current sheet moves earthward. An increase of the
magnetic flux corresponds to a high level of energy transport from the solar
wind to the magnetosphere, the cross-tail current enhancing simultaneously.
We assume that the magnetosphere tends to develop in such a way that the energy of
the solar-wind-magnetosphere
interaction remains minimal. An increase of the
tail lobe magnetic flux increases the flaring angle of the magnetosphere,
leading to an enhancement of the magnetosphere cross section as viewed from
the Sun.
If one considers the dependence of the magnetic flux on the distance to the inner
edge of the tail current sheet with
other
fixed
parameters (the subsolar distances
and current at the inner edge of the current sheet), one finds that
the magnetic flux decreases as the cross-tail current moves
earthward. Taking into account this feature, we can present the growth phase
as a sequence of two-step processes:
(1) the enhancement of
the cross-tail current and magnetic flux in tail lobe
and
(2) the earthward displacement of the current sheet.
The last step partially compensates the increase of the magnetic flux
and is limited by
magnetohydrodynamic
(MHD) equilibrium conditions in the tail. Thus
the earthward displacement of the current sheet reduces the energy of the
solar-wind-magnetosphere
interaction. It can also be noted that the
R1 and
R2 values cannot decrease without limit. The displacement is
limited by the pressure balance on the magnetopause and MHD equilibrium in the
tail.
Now the scenario of substorm growth and expansion can be described as follows:
When the IMF turns southward and energy transfer into the magnetosphere
increases,
both of the above mentioned distances ( R1 and
R2 ) decrease and
an increase of the tail flux ( F lobe ) begins. This process
has a
low probability to reach the critical values and thus low probability of
substorm onset. The tail lobe magnetic flux comes very close to the
"critical" value,
but the behavior of the model parameters ( R1 and
R2 ) does
not allow
F lobe to exceed it. When the IMF
turns northward,
the negative contribution of the Region 1 field-aligned currents to the magnetic
field in the dayside magnetosphere disappears, the magnetic field pressure in the
dayside magnetosphere increasing and the magnetopause moving away from the
Earth. Moreover, the positive contribution of the field-aligned currents to the
magnetic field in the nightside magnetosphere also disappears, the Ampere
force decreasing and the tail current sheet moving tailward. It is important
to note that changes in the IMF, which first appear at the subsolar point, can
change the current in the plasma sheet with some delay. This delay can be
estimated as 5-15 min.
During this period the following process will take place.
When IMF turns northward, the Region 1 field-aligned currents disappear,
the magnetic pressure at the dayside magnetosphere (near the subsolar point)
increasing. The magnetopause moves away from the Earth ( R1 increases). The same process begins in the tail:
the current sheet moves
tail-ward ( R2 increases).
During this period of time the tail lobe magnetic flux
F lobe does not decrease, but the
critical value does.
If, during the substorm
growth phase, a sufficient amount of energy
has been stored in the magnetospheric tail or
tail lobe, the magnetic flux comes very close to the "critical" value
(metastable state),
and it is quite possible for the
F lobe magnetic flux to reach and
exceed the critical value.
It is important to note, again, that the tail will react to the changes
in the IMF with some delay, but the Region 1 field-aligned currents will react
to these changes almost simultaneously.
This is the core of the substorm triggering
by the IMF northward turning
[Alexeev and Bobrovnikov, 1999].
Substorm Event of 10 January 1997
Although the scenario described in the previous section looks rather
promising, it is very important to test it with a real event,
using the
above described calculation scheme.
There is an interesting approach to the study of magnetospheric substorms
by using nonlinear filters
[e.g., Sitnov et al., 2000;
Vassiliadis et al., 1995].
The basic idea of these filters is to reproduce the output time series of
the substorm activity, mainly the
AL index, based on the input time series,
which are mainly the solar wind parameters and the
interplanetary magnetic field.
This technique can also be called a forecasting of the
AL index.
In such methods,
filters represent the magnetospheric dynamics,
no real magnetospheric processes being involved in the scheme.
In this case,
the magnetosphere acts as a "black box" with an input
gate for the solar wind data and an output gate for the magnetospheric indices.
Another widely used approach is a detailed investigation of the plasma
processes in various domains of the magnetosphere and
ionosphere. The essence of
such type of research is to study a sequence of local processes in the
magnetosphere by applying the sophisticated physical models of plasma processes
based on local MHD, particle, or wave simulation. When this approach is used, a
substorm as a global phenomenon becomes hidden.
As it was mentioned earlier, current studies support the idea
that a substorm
is a global instability of the magnetosphere. From this viewpoint the
former approach seems more adequate but veiling the magnetosphere
as a system of the magnetic field and plasma processes. In this paper we
would like to present the calculation scheme,
which resembles the filtering
approach but uses the real magnetospheric model in the core of the filter.
Let us now explain our choice of the substorm event. First of all,
it is a
typical and clear case of the substorm triggering by the IMF northward
turning, and it can thus support (or reject) our scenario of such events.
The other reason is that it presents a well-investigated substorm, and
most of the investigations support our ideas, especially those concerning
time delay between the changes in the IMF and substorm expansion onset.
Tsurutani et al. [1998] estimated it to be about 8-12 min,
and this value is also supported by the Lyons study
[Lyons et al., 1998].
In the latter paper the degradation of the ionospheric
convection related to the Region 1 field-aligned currents
was observed immediately after the IMF turned northward.
It presents the evidence that we are right
in assuming that the Region 1 field-aligned
currents play a key role in substorm triggering
by IMF northward turning.
Now we present the calculation scheme taking into account
the solar wind dynamic pressure, IMF
Bz component,
and time delay
(6-8 min)
between the changes in the IMF and the tail reaction to them.

|
|
Figure 4
|
Using the input data presented in
Figure 4,
let us
try to satisfy the pressure balance at the subsolar point.
Then the calculation scheme can be described as follows:
1. Take a reasonable value of
R1 (the magnetopause subsolar
distance) based on, for example,
Shue et al. [1997].
2. Calculate
R2 (the distance to the earthward edge of
the tail current sheet) with the simple formula
R2(t)=K(Bz(t-Dt))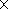 R1(t-Dt) (taking into account the time delay).
R1(t-Dt) (taking into account the time delay).
3. Take the value of the magnetic flux
F lobe=380 MWb
as the initial value for iterations.
4. Trace the inner edge of the current sheet ( R2 )
along a magnetic field line to the ionosphere, which can be
done in the Paraboloid model very simply.
5. Calculate the new flux
F lobe through the polar cap.
At this point we use the empirical relation between the auroral oval magnetic
flux, which can be calculated directly,
and the polar cap magnetic flux.
This relation depends on the IMF
Bz with the same delay.
6. Compare the new value of the magnetic flux with the old one
and repeat steps 4 and 5 to attain appropriate precision by changing
R2.
7. If the pressure balance is not attained, change
R1 with the appropriate step and repeat the scheme from step
2 except for the
initial magnetic flux,
which should now have the last calculated value.
|
|
Figure 5
|
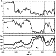
The results of the calculations are presented in
Figure 5.
At the
time, marked by the second vertical dashed line,
the magnetic flux in the tail
lobe exceeds its critical value. This time corresponds well to the auroral
intensifications observed onboard the polar spacecraft and by the ground-based
magnetometers.
Now it is time to answer the question: What can we obtain
from this scheme?
The answer is simple. As our scheme resembles the use of filters on the
solar wind data, it enables prediction of some features of a substorm. First
of all,
the time of the substorm expansion onset is predicted. It can be seen
from
Figure 4
that there are two IMF northward turnings during
the period of substorm development. However,
only the latter one produces
the substorm onset in reality and in our calculations.
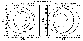
|
|
Figure 6
|
The major advantage of our method is that we have a set of model parameters
continuous in time. It enables various calculations based on
the Paraboloid model. They may be a calculation of
Dst index,
a calculation of the magnetic field at geostationary orbits
during substorm,
a field-line tracing that
reveals the dynamics of the magnetic field line
during the
substorm growth phase, and calculation of the auroral oval and polar cap
boundaries, which enables estimation of the substorm energetics. An example of
the results of such calculations is shown in
Figure 6.
This figure shows the auroral oval and polar cap boundaries for the
quiet magnetosphere (left) and for the late substorm growth phase.
A significant increase of the polar cap and auroral oval due to the substorm
development can be seen. The equatorward edge of the auroral oval approaches
60o of latitude and this is
in a good agreement whith
the ultraviolet images (UVI)
images from the polar spacecraft.
Our calculations of the polar cap behavior are also in a good agreement
(minimum at 0240 UT and maximum at 0337 UT) with the results
obtained by
Brittnacher et al. [1999].
Discussion and Conclusions
In conclusion, we would like to point
out the advantages and disadvantages of
our study. First of all, it concerns the Paraboloid model of the
magnetospheric magnetic field
and the appearance of the neutral point. The neutral point appears at the
inner edge of the tail current sheet close to the magnetopause, but
measurements show that this should happen close to the Earth-Sun line at
~10-20
RE.
This discrepancy can be explained by a relatively simple model of the tail
current system magnetic field. For example, this model has insufficient warp
of the inner edge around the Earth, so the magnetic field produced
by the tail current system in the near magnetopause region at the earthward
edge becomes overestimated. However, the displacement of this point would not
influence the essence of our approach. Assuming the substorm to be a global
instability of the magnetosphere, we would like to answer the
following question:
Why can the
IMF northward turning trigger the substorm,
and we would not like to answer
the question where the onset starts.
The presented scenario of the external triggering is based on
well-examined facts. It is well known that the magnetopause moves earthward
during the substorm growth phase and there exists a number of models of
the standoff distance
[e.g., Shue et al., 1997].
The enhancement of the lobe magnetic flux is also well known due to
measurements of the lobe magnetic field
and polar cap boundaries. The earthward displacement of the tail current
sheet is also confirmed by an increase of the auroral oval size. We
tried to clarify the causes of such magnetospheric dynamics and to create
the simplest scenario of the substorm growth phase.
We have a simple scenario, and we have a simple calculation scheme based
on simple assumptions on the model parameter dependencies upon the solar
wind and interplanetary magnetic field data. In the future we plan to develop
a better scenario of substorms, taking into account a greater number of
the input data and the model parameters.
Now, what can be inferred from our study? First, we would like to
support
the idea that a
substorm is a global magnetospheric phenomenon which comprises
many different processes with different spatial timescales
and intensity. To answer the questions when and where the
onset will start and what will be the intensity of the expansion phase, we need to
know
simultaneously the conditions in many regions of the magnetosphere, in the
ionosphere, and in the solar wind. We would also like to point out that it is
possible to determine the onset time and intensity of the substorm
expansion phase using the global model,
which yields the information about the
magnetic field in every magnetospheric region, and knowing the
conditions in the solar wind. Finally, the presented scenario of
substorms triggered by the IMF northward turning and the calculation scheme
can be described as a good approximation of real events.
However, it is important
to improve the scenario to be able to investigate a wider range of substorms.
References
Alexeev, I. I.,
Regular magnetic field in the Earth's magnetosphere,
Geomagn. Aeron. (in Russian), 18, 656, 1987.
Alexeev, I. I., and S. Yu. Bobrovnikov,
Tail current sheet dynamics during substorm,
Geomagn. Aeron.
(in Russian),
37, 24, 1997.
Alexeev, I. I., and S. Yu. Bobrovnikov,
Magnetospheric dynamics during substorm: external
substorm triggering,
in
Problems of Geocosmos, vol. 2,
Monogr.,
edited by V. S. Semenov,
Austrian Acad. of Sci.,
Vienna, Austria, 1999.
Alexeev, I. I., E. S. Belenkaya, and D. G. Sibeck,
Comparison of effects of field-aligned
and tail current on the structure of the magnetosphere,
Geomagn. Aeron. (in Russian), 37 (5), 19,
1997.
Baker, D. N., T. I. Pulkkinen, V. Angelopoulos, W. Baumjohann, and
R. L. McPheron,
Neutral line model of substorm: Past results and present view,
J. Geophys. Res., 101, 12,975, 1996.
Baker, D. N., T. I. Pulkkinen, J. Buchner, and A. J. Klimas,
Substorms: A global
instability of the magnetosphere-ionosphere system,
J. Geophys. Res., 104, 14,601,
1999.
Brittnacher, M., M. Fillingim, G. Parks, G. Germany, and
J. Spann,
Polar cap
and boundary motion during substorms, J. Geophys. Res., 104,
12,251, 1999.
Caan, M. N., R. L. McPherron, and C. T. Russell,
Substorms and interplanetary magnetic
field effects on the geomagnetic tail lobes,
J. Geophys. Res., 80, 191, 1975.
Lyons, L. R., A new theory for magnetospheric substorms,
J. Geophys. Res., 100, 19,065, 1995.
Lyons, L. R., Substorms: Fundamental
observation features, distinction from other
disturbances, and external triggering,
J. Geophys. Res., 101, 13,011,
1996.
Lyons, L. R., G. T. Blanchard, and K. B. Baker,
Substorm onset: the result of IMF-driven
reduction in large-scale convection,
in
Proceedings of the Fourth International Conference on Substorms,
edited by Y. Kamide, p. 265, Terra Sci., Tokyo, Japan, 1998.
McPherron, R. L., T. Terasawa, and A. Nishida,
Solar wind triggering of substorm
onset,
J. Geophys. Geoelectr., 38, 1089, 1986.
Nishida, A., and
N. Mukai, Response of the near-Earth magnetotail to a northern
turning of the IMF,
Geophys. Res. Lett., 24 (8), 943, 1997.
Roelof, E. C., and D. G. Sibeck,
Correction to "Magnetopause shape
as a bivariate function of interplanetary
magnetic field
Bz and solar wind dynamic pressure,
J. Geophys. Res., 98, 21,421, 1993,"
J. Geophys. Res., 99, 8787, 1993.
Rostoker, G., Triggering of expansion phase
intensifications of magnetospheric
substorm by northward turning of
the interplanetary magnetic field,
J. Geophys. Res., 88, 6981, 1983.
Rostoker, G., M. Mareschal, and J. C. Samson,
Response of dayside net downward field-aligned
current to changes in the interplanetary magnetic
field and to substorm perturbations,
J. Geophys. Res., 87, 3489, 1982.
Shue, J.-H., J. K. Chao, H. C. Fu, and C. T. Russel,
A new function form to study the
solar wind control of the magnetopause
size and shape,
J. Geophys. Res., 102, 9497, 1997.
Sitnov, M. I., A. S. Sharma, K. Papadopoulos, D. Vassiliadis,
J. A. Valdiva, A. J. Klimas, and D. N. Baker, Phase
transition-like
behavior of the magnetosphere during substorms,
J. Geophys. Res., 105, 12,955,
2000.
Troshichev, O. A., A. L. Kotikov,
B. D. Bolotinskaya, and
V. G. Andrezen,
Influence
of the IMF azimuthal component on magnetospheric
substorm dynamics,
J. Geophys. Geoelectr., 38, 1075, 1986.
Tsurutani, B. T.,
J. K. Arballo, G. S. Lakhina, C. M. Ho,
J. M. Ajello, and J. S. Pickett,
A CME loop and January 10, 1997 first substorm,
Proceedings of the Fourth International Conference on Substorms,
edited by Y. Kamide, p. 309, Terra Sci., Tokyo, Japan, 1998.
Tsyganenko, N. A., and D. G. Sibeck,
Concerning flux
erosion from the dayside magnetosphere,
J. Geophys. Res., 99, 13,425,
1994.
Vassiliadis, D. V., A. J. Klimas, D. N. Baker, and D. A. Roberts,
A description of solar
wind-magnetosphere coupling based on nonlinear filters,
J. Geophys. Res., 100, 3495, 1995.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on January 27, 2002.
 1 hour for the storm on August
19, 1978.
Lyons [1995]
noted that sudden changes in the IMF
By could also control the substorm onset.
Troshichev et al. [1986] showed
that a decrease of
|By| down to zero can trigger substorm onset.
McPherron et al. [1986]
studied the IMF
Bz at the time of onsets and showed that 44% of 126 events
were directly
related to the IMF northward turning,
and 29% of events occurred at a steady negative
Bz.
Taking into account changes in the IMF
By investigated by McPherron,
Lyons [1996]
revealed a distinct relation between sudden IMF
changes and substorm onsets.
Lyons [1995]
proposed a substorm model
that explains the IMF triggering of a substorm expansion by a
decrease of the electric
field in the near-Earth magnetotail and, as a consequence, development of
field-aligned currents.
Nishida [1997]
carried out recently a case study
and found no evidence for the Lyons theory. They have found an
increase of the electric field just before substorm expansion,
a fact contradicting
the Lyons
theory. Thus there is no commonly accepted theory of the mechanism
that connects changes in the IMF to a substorm expansion onset.
1 hour for the storm on August
19, 1978.
Lyons [1995]
noted that sudden changes in the IMF
By could also control the substorm onset.
Troshichev et al. [1986] showed
that a decrease of
|By| down to zero can trigger substorm onset.
McPherron et al. [1986]
studied the IMF
Bz at the time of onsets and showed that 44% of 126 events
were directly
related to the IMF northward turning,
and 29% of events occurred at a steady negative
Bz.
Taking into account changes in the IMF
By investigated by McPherron,
Lyons [1996]
revealed a distinct relation between sudden IMF
changes and substorm onsets.
Lyons [1995]
proposed a substorm model
that explains the IMF triggering of a substorm expansion by a
decrease of the electric
field in the near-Earth magnetotail and, as a consequence, development of
field-aligned currents.
Nishida [1997]
carried out recently a case study
and found no evidence for the Lyons theory. They have found an
increase of the electric field just before substorm expansion,
a fact contradicting
the Lyons
theory. Thus there is no commonly accepted theory of the mechanism
that connects changes in the IMF to a substorm expansion onset.



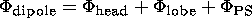

 R1(t-Dt) (taking into account the time delay).
R1(t-Dt) (taking into account the time delay).