Investigation of MHD slow shocks propagating along the Io flux tube

N. V. Erkaev

Institute of Computational Modelling, Russian Academy of Sciences, Krasnoyarsk, Russia

V. S. Semenov

Physical Institute, St. Petersburg University, St. Petersburg, Russia

V. A. Shaidurov

Institute of Computational Modelling, Russian Academy of Sciences, and State University, Krasnoyarsk, Russia

D. Langmayr, H. K. Biernat, and H. O. Rucker

Space Research Institute, Austrian Academy of Sciences, Graz, Austria

Received 18 April 2001, published online 24 January 2002

Contents

Abstract

Introduction

In 1954, Burke and Franklin [1955] discovered radio emissions from Jupiter at 22.2 MHz. Subsequent observations established the strong control of these decametric emissions (DAM) by the satellite Io. Considerable theoretical and experimental attention has been given to explain this strong control. These examinations are based on the global interaction between Io and Jupiter. It is generally believed that the main factors of the plasma torus-Io-Jupiter electrodynamic interaction are Alfvén wings which are standing Alfvén waves attached to the satellite [Bagenal and Leblanc, 1988; Neubauer, 1980]. Slow waves are expected to be much less intensive and therefore these magnetohydrodynamic (MHD) waves received less attention although they have been investigated in several publications [Kopp, 1996; Krisko and Hill, 1991; Linker et al., 1991; Wright and Schwartz, 1990]. Unfortunately, these studies were restricted to the vicinity of Io, whereas the most important and interesting effects are expected when a slow wave propagates into the region with strong magnetic field above the ionosphere of Jupiter. The purpose of this paper is outlined as follows: We follow a slow wave traveling from its source point at Io toward Jupiter, estimate the consequences of this propagation process along the Io flux tube, and finally find some possible application for the DAM radiation.

There are at least two possibilities how the slow mode waves can be excited in the vicinity of Io. The first one is connected with the high volcanic activity of Io. Direct volcanic plumes at Io cannot supply the bulk of the torus plasma, because the characteristic plume speed is much less than the escape velocity (2.6 km s ^-1 ) [Hill et al., 1983]. Nevertheless, small portions of volcanic material are stripped by a cometary type of interaction with the plasma in the Io torus. Observations show that the plasma density in the Io torus remains roughly constant, although the volcanic activity on Io is sporadic. Probably there is a feedback mechanism due to which an increase of the mass in the plasma torus causes a corresponding increase in the loss [Brown and Bouchez, 1997]. However, the details of this process are still poorly understood, the characteristic relaxation times are unknown, and so far, it is difficult to calculate the increase in the plasma pressure produced by a concrete volcanic eruption. The generation of kinetic Alfvén waves produced by volcanic eruption at Io has been recently investigated by Das and Ip [[2000].

Figure 1

The second possibility for the development of a pressure pulse might be the flow of the torus plasma around Io. Analytical and numerical studies show a rather complicated picture of the gas pressure distribution with firstly an enhancement followed by rarefaction, but slow mode wings are clearly seen [Kopp, 1996; Linker et al., 1991]. The gas pressure enhancement in the maximum is relatively small (~30%) and increases with mass loading [Kopp, 1996]. As noted, the exact mass loading rate is rather uncertain. Therefore it is a good idea to use experimental data for the estimation of the pressure pulse intensity. These experimental data are provided by the Galileo spacecraft. Figure 1 shows a direct observation of the plasma pressure in the vicinity of Io at a closest approach of about 0.5  R _Io (900 km) [Frank et al., 1996]. As can be seen, the pressure is enhanced by a factor ~2-3. However, after this increase, the spacecraft crossed the cold ionosphere of Io, and thus the data points are not valid for the warm plasma in the torus. Extrapolating the increasing curve with a Gaussian function reveals that the real enhancement of the gas pressure must be in the range ~6-8, as Figure 1 shows.

Moving along its orbit, Io is followed by a wake of disturbed plasma pressure. In the frame of Io, these wings look like a steady-state structure. However, in a frame of a given magnetic flux tube passed by Io, the plasma perturbations are not steady: The plasma pressure is a function of time.

The background plasma parameters of the magnetic flux tube are considered to be in equilibrium. This equilibrium is reached after some relaxation time, when a new portion of plasma injected into the tube is precipitating due to the loss process. This relaxation time should be much less than the period of the Io motion along its orbit. The latter condition seems to be valid for the Io-Jupiter interaction.

In the following, we suggest that there is a positive pressure pulse of an amplitude of about 6 in a flux tube and calculate the slow mode propagation toward Jupiter. From the physical point of view, crossing of the fresh Io flux tube is similar to an explosion in this Io flux tube, but an explosion of a very specific type. The peculiar feature of this explosion stems from two basic facts. First, the slow mode wave is guided along the magnetic field (one-dimensional (1-D) explosion), and second, the slow wave propagates inside a dipole flux tube with progressively decreasing cross section. For the Io flux tube ( L 6 ) the cross section of the tube decreases 380 times within a distance of 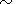7.13 R _J, and in addition, the magnetic pressure increases 1.5 10⁵ times. As a result, the flow velocity has to increase toward Jupiter rather than to decrease, as it usually happens after a regular explosion.

So, a scenario that is justified in this paper can be described as follows (see Figure 2): A pressure pulse produced near Io generates two slow waves propagating along the Io flux tube into the southern and northern ionosphere of Jupiter. These slow waves are quickly converted into nonlinear waves due to a steepening mechanism with a supersonic flow behind the shock front. The flow velocity behind the shock increases in the course of the propagation to Jupiter and reaches values of the order of the initial Alfvénic velocity (~150 km s ^-1 ) at the site of Io. In its turn, the plasma flow streaming along the Io flux tube has to generate a field-aligned potential difference due to the Alfvén mechanism [see Serizava and Sato, 1984], which can be as large as 1 kV. Therefore the slow mode wave mechanism seems to contribute to the Io-controlled aurora and radio emissions together with the generally accepted Alfvén wings model.

Mathematical Formulation of the Problem

Figure 2

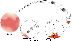
From the mathematical point of view we have to simulate a local explosion inside the Io flux tube. The geometrical situation of the problem is illustrated in Figure 2.

To describe the perturbations of the magnetic field and the plasma parameters, we basically apply the system of ideal MHD equations without dissipation

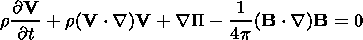(1)

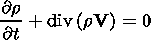(2)

(3)

(4)

(5)

Here r, V, P, and B are the mass density, bulk velocity, plasma pressure, and magnetic field, respectively. The quantity P denotes the total pressure (the sum of magnetic and plasma pressures), P = P + B²/(8p), and k is the polytropic exponent.

Considering the case of low plasma beta, we assume the total pressure to be approximately equal to the dipole magnetic pressure. Therefore in this approximation the total pressure is a known function of the distance S along the tube.

From the momentum equation (1), we obtain the equation for the field-aligned velocity component

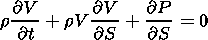(6)

where S is the distance measured along the tube.

The conservation law for the magnetic flux results in a new equation for the magnetic field, i.e., B F = Y, where Y is the magnetic flux, which is constant along the flux tube, and F is the cross section of the magnetic flux tube. For an ideally conducting plasma, the magnetic field is frozen-in and the magnetic flux is not a function of time for a given flux tube.

The mass conservation law applied to the thin tube yields the continuity equation in the following form

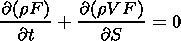(7)

Substituting the cross section expressed through the magnetic field strength, we obtain the equation

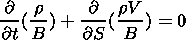(8)

The system of relations (6)-(8) is closed by the entropy equation

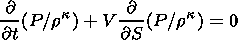(9)

We normalize the magnetic field and the plasma parameters as follows:

(10)

Here R _J is the Jupiter radius, V_A0 is the Alfvén velocity, and r₀, B₀ are the mass density and magnetic field strength in vicinity of Io. The undisturbed plasma parameters along the magnetic field line are considered to satisfy the equilibrium equation

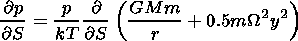(11)

where G is the gravitational constant, m is the average mass of particles, M is the mass of Jupiter, r is the radial distance from the center of Jupiter, y is the distance to the rotational axis, k is the Boltzman constant, T is the temperature assumed to be constant along the tube, and W is the angular speed of Jupiter, respectively.

The plasma parameters at the Io orbit used in our calculations are the following [Neubauer, 1998]:

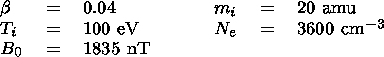(12)

These parameters correspond to an Alfvén speed of V_a = 150 km s ^-1. Similar parameters were used also by Combi et al. [1998] for the numerical simulation of mass loading in the vicinity of Io.

Next, we introduce the material coordinate a, which is determined as follows:

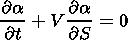(13)

In accordance with the equation above, the quantity a is constant along the trajectory of the particle.

From the definition of a, a differential relation is obtained

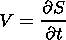(14)

This is the partial derivative with respect to time under a constant a.

Using equations (8), (13), and (14), we obtain a relation between a and B

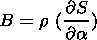(15)

This coordinate a is a particular case of the so-called frozen-in coordinates introduced by Pudovkin and Semenov [1977] for ideal magnetohydrodynamics.

Using the independent coordinate a instead of S, we finally obtain the system of equations

(16)

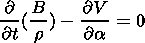(17)

(18)

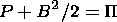(19)

(20)

For the computation of the shock discontinuities, the adiabatic equation is not appropriate, because the entropy has a jump at the shock. Therefore to calculate the shock fronts, the adiabatic equation has to be replaced by the more general energy equation:

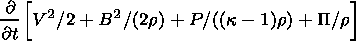(21)

To solve the problem, we use a two-step differential numerical method with a right-angled grid. At the first step, the method of characteristics is used to calculate the density, velocity, and magnetic field in the intermediate grid points labeled with half-integer numbers. Along the characteristics we have the following equations:

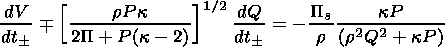where Q = B/r, and

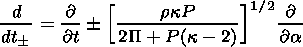For the second step, the plasma parameters and the magnetic field are calculated in the main grid points labeled with integer numbers

Here the different signs correspond to the intermediate points i 0.5 and t + 0.5 , for the parameters marked by 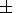and .

The gas pressure and density are calculated from the system of algebraic equations

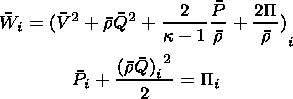This variant of the differential scheme is appropriate for the computation of plasma parameters in the tube where the total pressure is not very large compared to the plasma pressure. It is important to note that the total pressure varies along the magnetic flux tube from Io to Jupiter by a factor of 1.5 10⁵. In the case of very large magnetic pressure, the plasma pressure obtained from the equation for the total pressure, is the difference between two very large quantities, the total and the magnetic pressures. This brings about an inaccuracy in the numerical solution.

Therefore the entropy equation is more convenient for the computation of the plasma pressure in a region of very large total pressure. In such a case, the shock front must be separated, thereby using the jump conditions for the slow shock.

In our calculations, the energy equation together with equations (16)-(20) are only used for the description of the first stage of the formation of the slow shock, produced by the local enhancement of the plasma pressure near Io. After that, when the shock front is formed, we calculate the propagation of the slow shock along the magnetic flux tube toward Jupiter by separating the shock front and using the system with the entropy equation behind the shock.

Results of MHD Simulation

Figure 3

The first stage of the slow mode wave generation is shown in Figure 3. It can be clearly seen that the initial pressure pulse is quickly divided into two waves propagating along the flux tube in opposite directions. The amplitudes of these waves are decreasing in the course of time, the leading fronts getting more and more steep, and eventually slow waves are converted into shocks.

The initial stage is very similar to a classical 1-D explosion, and the behavior of all parameters (pressure, density, velocity) is also quite analogous. Thus if the tube cross section would not change any more, the process of the wave propagation could be easily predicted: Slow shocks would travel along the flux tube and be gradually damped with decreasing flow velocity behind the shock fronts.

Figure 4

Figure 5

However, the flux tube cross section is inversely proportional to the magnetic field strength and therefore has to decrease as r³ due to the dipole field configuration. Hence the plasma flow has to move into a more and more narrow flux tube, and in addition, the total pressure is increasing even more rapidly as r^-6. As a result, the wave amplitude firstly stays roughly constant as long as damping, due to the expansion, is balanced by the narrow channel effect. After that, the tube cross section starts to decrease so rapidly that the wave amplitude begins to enhance, as Figure 4 shows. All these three stages are especially evident in Figure 5 where the positions of the maximum values of the plasma pressure, density, and velocity are shown. The first stage, corresponding to a classical explosion, is rather small, restricted to the proximity of Io. It can be seen in numerical simulations of the plasma torus flow around Io [Kopp, 1996; Linker et al., 1991]. However, in their simulations the pressure perturbations for the compression (there are also rarefactions that we do not consider here) are weaker than our pressure quantity. This discrepancy stems from the fact that the amplitude of the pressure variation is strongly dependent on the mass loading rate, which is poorly known so far. Strong plasma pressure perturbations are related with a large mass loading rate [Combi, 1998; Kopp, 1996]. In our simulations, we use the initial pressure variation amplitude of the factor 6 from the Galileo observations [Frank et al., 1996].

The second stage is characterized by approximately constant parameters and is the most prolonged one. Nearly all the way from Io to Jupiter expanding, damping, and narrow channel effects effectively compensate each other.

By the arrival at the point ( S 6.3 R _J ), the plasma velocity reaches its maximum value 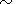0.9 V_A0. After the maximum point, the velocity starts to decrease near Jupiter because of the enhancement of the background pressure due to the gravitational force.

As it was shown, an explosion in a flux tube with an increasing magnetic field and correspondingly decreasing of the tube cross section is considerably different from an usual 1-D explosion. The narrow channel effect leads to an intensification of the propagating wave rather than to damping due to its expansion. This effect might be important not only in the case of Io but also for all other situations on the Sun or on the other planets where pressure pulses can be produced inside a thin flux tube.

Field-Aligned Electric Field

As we saw, pressure pulses created near Io eventually generate slow shocks accompanied by an accelerated plasma flow behind the shock. It is known that a supersonic flow produces a field-aligned electric field [Serizava and Sato, 1984]. It is a fact that if the mass velocity of ions is much bigger then the thermal velocity (supersonic flow), then most of the ions must have small pitch angles, whereas the electrons, for which the thermal velocity is much greater, should not be noticeably disturbed. As a result, the mirror points of the streaming protons and electrons are located at different positions along the flux tube leading to a charge separation and the occurrence of a field-aligned electric field. To calculate the potential difference, we use the method of Serizava and Sato [1984], modified for the Io flux tube with its very special types of ions. This method has been checked with numerical simulations [Schriver, 1999], and both results coincide within 5%, which is accurate enough for our purpose.

As a starting point for the mathematical analysis, we assume the different plasma components at the initial position to be modeled by the so-called parallel beam distribution function given as

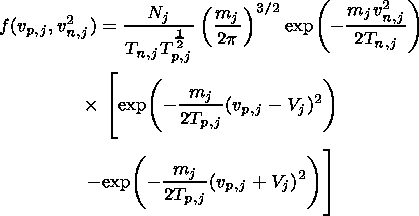(22)

where N, m, v, T, and V refer to particle number density, mass, velocity, temperature in energy units, and flow velocity, respectively. Subscript j denotes the particle species and subscripts p and n characterize the parallel and normal components of the relevant quantities with respect to the magnetic field.

In the following, we explicitly use the particle conservation along the magnetic flux tube and assume that there is no field-aligned current present. In other words, the flux carried by the reflected electron contribution F_e has to be equal to the reflected ion flux F_i,s. Thus we have

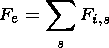(23)

where s denotes the different kinds of ions. This current-free condition together with the initial charge neutrality lead us to

(24)

where subscript zero refers to quantities at the initial position.

As a next step, we evaluate the respective reflected fluxes carried by the different species of particles. Therefore we start with the consideration of the magnetic moment m, characterizing the particle's perpendicular velocity. This quantity is conserved as the particles precipitate toward higher magnetic field strengths. Hence assuming a dipole magnetic field configuration leads us to

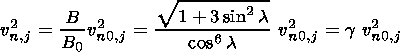(25)

where l denotes the magnetic latitude, and we introduced the parameter g referring to the ratio of the magnetic fields.

Additionally, from the conservation of energy we have

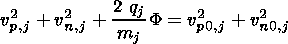(26)

where F denotes the electric potential difference, which is initially zero, and q refers to the charge. Substituting relation (25) into (26) yields

(27)

It is reasonable that at the mirror points the parallel component of the particle velocity vanishes. Thus the right-hand side of expression (26) determines a curve in the velocity space separating the reflected particles from those passing through. The corresponding fluxes are now derived by calculating the first moment of the distribution function (22), with regard to the particular contributions, which carry the reflected flux. The result is as follows

(28)

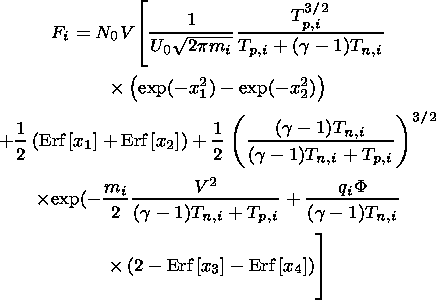(29)

with

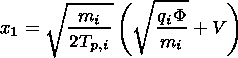(30)

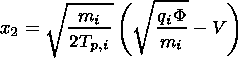(31)

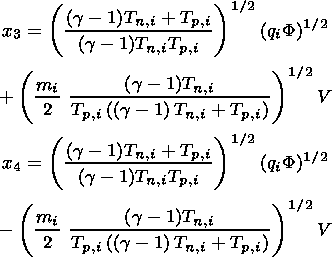(32)

where Erf[ x ] is the error function. The current-free condition (23) permits to solve expression (28) together with (29) numerically to obtain the potential as a function of the distance from the equatorial plane along the flux tube S normalized to the Jupiter radius R _J.

As the electrons pass the developed potential they pick up the potential drop and are effectively accelerated. The electron velocity can be determined by

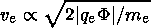(33)

Figure 6

To simulate the conditions in the Io flux tube, we assume the plasma stream to contain hot anisotropic ions (S ⁺ and O ⁺ ) with T_n,i = 5 and T_p,i = 200 eV, and isotropic electrons with T_n,e = T_p,e = 150 eV, following thereby [Mei et al., 1995]. The electric potential calculated for the different plasma velocities and the ratio of the current and thermal speeds of electrons accelerated by the potential difference are shown in Figure 6 as functions of the distance along the magnetic flux tube.

We can summarize the results of our investigations as follows: First, we note that the potential tends to saturate toward a maximum value. The prevailing quantities determining the strength of this maximum potential are the flow speed and the composition of the ion population. As shown in Figure 6, the potential increases with the flow speed. In fact, the strength of the saturation potential is proportional to the flow energy of the ion contribution and therefore increases with the square of the ion flow velocity. Now, the influence of the mass of the streaming ion populations can be clarified. Heavy ion constituents lead to an enhancement of the potential drop, whereas light ion populations do not effectively contribute to the potential difference. For our purpose, the ion population is assumed to consist of heavy sulfur and oxygen, which leads to a considerable high potential drop.

The main result of this study is that the amount of the maximum potential difference can be of the order of 1 kV. As the precipitating electrons pass through the developed potential they pick up the potential drop and are effectively accelerated to energies of the order of the strength of the potential drop. The electron velocity can be determined by v_e 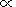2 q_e F / m_e. These energetic electrons play a crucial role in the explanation of aurora on Jupiter and the DAM radio emissions [Hill et al., 1983; Wu, 1987].

Discussion

In this paper we tried to emphasize the role of slow mode waves, which are not only important in the course of the torus plasma flow around Io [Kopp, 1996; Krisko and Hill, 1991; Linker et al., 1991; Wright and Schwartz, 1990] but can also be responsible for some specific phenomena such as aurora or DAM radiation together with Alfvén waves. The latter mechanism is much more powerful, and as far as aurora is concerned, we suggest the following interpretation: Direct observations of the Io footprint aurora show that there is a bright leading point corresponding to the projection of Io. In addition, a diffuse fainter emission is observed, which is extended in longitude with several bright spots in the tail [Connerney et al., 1999]. The leader is certainly connected with the first Alfvén wave arrival at the Jovian ionosphere. The trailing spots have been interpreted as arrivals of reflected Alvfén waves [Connerney et al., 1999]. Our point is that one of these bright spots in the tail might be connected with the arrival of the slow shock. The DAM emissions are also believed to be caused by Alfvén wings having their source near the instantaneous Io flux tube [Bagenal, 1983; Menietti and Curran, 1990]. However, studies of Queinnec and Zarka [1998] show that some parts of the DAM emission, in particular the Io-B radiation, have a 30^o- 50^o lag of the source field line and the instantaneous Io flux tube for the maximum emission frequency. This lag would require an unrealistically increasing plasma density (more than 10 times higher than that used by Bagenal [1983]) to explain the propagation time of Alfvén waves.

Our study shows that the role of this carrier can be played by nonlinear slow wave. As it was pointed out, the consequence of the slow shock propagation is a strong plasma flow behind the shock front, which in turn leads to a field-aligned electric potential difference of the order of 1 kV. The nonlinear wave is much slower than an Alfvén wave and gives the needed longitude lag in the range of 30^o-50^o. Therefore we believe that the slow wave mechanism can also be responsible for some parts of the DAM emissions.

Acknowledgments

References

Bagenal, F., Alfvén wave propagation in the Io plasma torus, J. Geophys. Res., 88, 3013, 1983.

Bagenal, F., and Y. Leblanc, Io's Alfvén wave pattern and the Jovian decametric arcs, Astron. Astrophys., 197, 311, 1988.

Brown, M. E., and A. H. Bouchez, The response of Jupiter's magnetosphere to an outburst on Io, Science, 278, 268, 1997.

Burke, B. F., and K. L. Franklin, Observations of a variable radio source associated with the planet Jupiter, J. Geophys. Res., 60, 213, 1955.

Combi, M. R., T. I. Gombosi, and D. L. DeZeeuw, Io's plasma environment during the Galileo flyby: Global three-dimensional MHD modeling with adaptive mesh refinement, J. Geophys. Res., 103, 9071, 1998.

Connerney, J. E. P., T. Sato, and J. T. Clarke, Tracking the Io flux tube footpoints, in The 31st Annual Meeting of the AAS Division for Planetary Sciences, Am. Astron. Soc., Washington, D.C., 1999.

Das, A. C., and W.-H. Ip, Field-aligned current and particle acceleration in the near-Io plasma torus, Planet. Space Sci., 48, 127, 2000.

Frank, L. A., W. R. Paterson, K. L. Ackerson, V. M. Vasyliunas, F. V. Coronity, and S. J. Bolton, Plasma observations at Io with the Galileo spacecraft, Science, 274, 394, 1996.

Hill, T. W., A. J. Dessler, and C. K. Goertz, Magnetospheric models, in Physics of the Jovian Magnetosphere, edited by A. J. Dessler, Cambridge Univ. Press, New York, 1983.

Kopp, A., Modification of the electrodynamic interaction between Jupiter and Io due to mass loading effects, J. Geophys. Res., 101, 24,943, 1996.

Krisko, P. H., and T. W. Hill, Two-dimensional model of a slow-mode expansion fan at Io, Geophys. Res. Lett., 18 (11), 1947, 1991.

Linker, J. A., M. G. Kivelson, and R. J. Walker, A three-dimensional MHD simulation of plasma flow past Io, J. Geophys. Res., 96, 21,037, 1991.

Mei, Y., R. M. Thorne, and F. Bagenal, Analytic model for the density distribution in the Io plasma torus, J. Geophys. Res., 100, 1823, 1995.

Menietti, J. D., and D. B. Curran, Instantaneous Io flux tube as the source of Jovian DAM: Possible second harmonic emissions, J. Geophys. Res., 95, 21,273, 1990.

Neubauer, F. M., Nonlinear standing Alfvén wave current system at Io: Theory, J. Geophys. Res., 85, 1171, 1980.

Neubauer, F. M., The sub-Alfvénic interaction of the Galilean satellites with the Jovian magnetosphere, J. Geophys. Res., 103 (9), 19,843, 1998.

Pudovkin, M. S., and V. S. Semenov, Stationary frozen-in coordinate system, Ann. Geophys., 33, 429, 1977.

Queinnec, J., and P. Zarka, Io-controlled arcs and Io-Jupiter interaction, J. Geophys. Res., 103, 26,649, 1998.

Schriver, D., Particle simulation of the auroral zone showing parallel electric fields, waves, and plasma acceleration, J. Geophys. Res., 104, 14,655, 1999.

Serizava, Y., and T. Sato, Generation of large scale potential difference by currentless plasma jets along the mirror field, Geophys. Res. Lett., 11 (6), 595, 1984.

Wright, A. N., and S. J. Schwartz, The equilibrium of a conducting body embedded in a flowing plasma, J. Geophys. Res., 95, 4027, 1990.

Wu, C. S., Cyclotron maser instability and its applications, in Planetary Radio Emissions II, edited by H. O. Rucker, S. J. Bauer, and B. M . Pedersen, pp. 339, Austrian Acad. of Sci. Press, Graz, Austria, 1988.