B, generated by the current layer with
density,
j,
is determined by Maxwell's equation
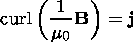 | (12) |
Because of the assumption of one-dimensionality
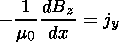 | (13) |
Magnetic fields generated by the currents carried by the
magnetosheath and
magnetospheric ions,
Bz sh(x) and
Bz sp(x),
respectively, can be found by integration the
equations for
jay
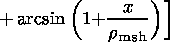 | (14) |
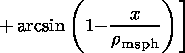 | (15) |
where
B0 sh and
B0 sp are the constants of integration,
giving the values that the magnetic field
Bz(x)=Bz sh(x)+Bz
sp(x) approaches as
x goes to
-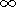 and to
+
and to
+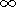 :
B msph0 and
B msh0, respectively
(the input parameters of the model).
Taking into account that
.Bz sh(x)x=-
:
B msph0 and
B msh0, respectively
(the input parameters of the model).
Taking into account that
.Bz sh(x)x=-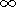 =.B z sh(x)x=-2r msh,
.Bz sp(x)x=-
=.B z sh(x)x=-2r msh,
.Bz sp(x)x=-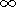 =.B z sp(x)x=0,
.Bz sh(x)x=
=.B z sp(x)x=0,
.Bz sh(x)x=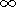 =.B z sh(x)x=0,
and
.Bz sp(x)x=
=.B z sh(x)x=0,
and
.Bz sp(x)x=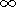 = .B z sp(x)x=2r msph,
we obtain
= .B z sp(x)x=2r msph,
we obtain
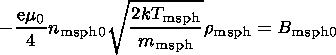 | (16) |
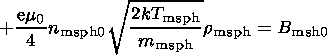 | (17) |
and at
x=0
 | (18) |
If
the value
.Bz(x)x=0 is known, the solution
of the system of three equations
(16)-(18)
with three variables --
B0 B0
sh+B0 sp,
r msh, and
r msph --
can be found.
Quantity
.Bz(x)x=0 can be defined from the
equilibrium condition
for each current sheet boundary.
For the existence of the described current structure, the pressure
balance
must be fulfilled at the edges of each current layer:
B0
sh+B0 sp,
r msh, and
r msph --
can be found.
Quantity
.Bz(x)x=0 can be defined from the
equilibrium condition
for each current sheet boundary.
For the existence of the described current structure, the pressure
balance
must be fulfilled at the edges of each current layer:
 | (19) |
where
P tot is the total pressure,
Pxx is the plasma pressure, and
B is the total magnetic field
strength. So, this condition is valid at the boundary between two
current
sheets, at
x=0, and determines the value
.Bz(x)x=0:
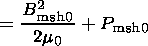 | (20) |
From
(8),
(16)-(18), and
(20)
we conclude that
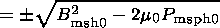 | (21) |
Here we will consider only the sign "
+ " in front of the square
root (the
northward magnetic field inside the magnetopause).
The corresponding solution for the system of equations
(16)-(18) is:
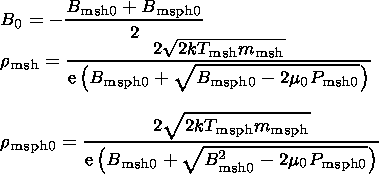 | (22) |
This solution gives the constant of integration,
B0,
satisfying the magnetic field boundary conditions;
-B0 plays the role of the "background" external
magnetic field existing in the
problem;
r msh and
r msph are
the half-thickness of the current layers created by the
magnetosheath and magnetospheric ions, respectively, in the
steady-state case.
The values of magnetic fields in which ion gyroradii should be
calculated are
determined.
Equation (21)
defines the minimum value of the magnetic field strength inside the
magnetopause at the boundary between two current sheets.
The linear integral current density,
Jay, for the
magnetosheath
and magnetospheric ion currents are, respectively,
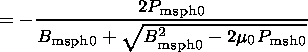 | (23) |
The resulting magnetic field
corresponding to the two current layers
at the subsolar low-shear magnetopause
is
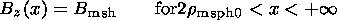 | (24) |
A peculiarity of the obtained solution
is due to our particular choice of the distribution function.
It should be noted that
in figures demonstrating calculations performed by
Lee and Kan [1979a],
for northward IMF, one can see at the magnetopause two pairs of
antiparallel currents carried by the magnetospheric and magnetosheath
ions and electrons. However, in the text by
Lee and Kan [1979a],
the existence of antiparallel magnetopause currents is not even
mentioned.
Moreover, the authors considered that the magnitude of the magnetic
field
intensity inside the magnetopause current sheet should be greater
than that
on the two sides. This situation opposes that presented here.
3.5. Comparison With Observations
For comparison with observations we use 4.35-s data from the
AMPTE/IRM satellite
[Phan et al., 1994],
which provide dayside plasma and magnetic field
observations obtained on 13 and 24 October 1985
(see Figure 4 and Figure 3 from
Phan et al. [1994]).
On 13 October 1985, the magnetopause crossing was at
1132:07 UT for the low magnetic shear which was less than
30o.
The magnetosheath magnetic field direction in this case remained
rather steady for at least 30 min prior to the magnetopause
encounter.
In this time, a decrease in the magnetic field
B (from
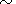 67 nT
to
67 nT
to
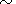 57 nT) and an increase of the plasma pressure,
p pla (from
57 nT) and an increase of the plasma pressure,
p pla (from
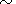 0.4 nPa to
0.4 nPa to
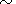 0.8 nPa),
were
observed, followed by a reverse increase of
B to
0.8 nPa),
were
observed, followed by a reverse increase of
B to
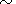 65 nT
and decrease of
p pla to
65 nT
and decrease of
p pla to
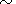 0.5 nPa.
0.5 nPa.
Taking the
observed data for this event as the input values, we can
calculate the model
"background" external
magnetic field, the minimum magnetic field strength
in the magnetopause double-layer current structure, and the
character length scale of each current layer.
According to
Phan et al. [1994],
the magnetosheath parameters
were:
n msh 8 cm-3,
T msh
8 cm-3,
T msh 4
4 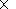 106 K,
B msh
106 K,
B msh 67 nT,
and the magnetospheric parameters near the
magnetopause were:
n msph
67 nT,
and the magnetospheric parameters near the
magnetopause were:
n msph 2 cm-3,
T msph
2 cm-3,
T msph 20
20 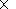 106 K,
and
B msph
106 K,
and
B msph 65 nT.
For these values, we obtain for the
magnetosheath protons:
V msh
65 nT.
For these values, we obtain for the
magnetosheath protons:
V msh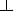
 180 km s
-1,
r msh
180 km s
-1,
r msh 44 km,
jy mshmax
44 km,
jy mshmax 1
1 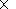 10-7 A m
-2,
and
J msh
10-7 A m
-2,
and
J msh 1.3
1.3 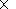 10-2 A m
-1.
10-2 A m
-1.
Similarly, for the magnetospheric protons:
The thermal velocity
V msph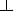
 400 km s
-1,
r msph
400 km s
-1,
r msph 94 km,
j msphy
94 km,
j msphy -0.6
-0.6 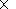 10 -7 A m
-2,
and
J msph
10 -7 A m
-2,
and
J msph  -1.6
-1.6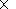 10-2 A m
-1.
The "background" magnetic field
-B0=66 nT,
and the minimum magnetic field
at the magnetopause, between two current layers, is
Bz min=57 nT,
which agrees well with observations (
10-2 A m
-1.
The "background" magnetic field
-B0=66 nT,
and the minimum magnetic field
at the magnetopause, between two current layers, is
Bz min=57 nT,
which agrees well with observations ( 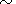 57 nT).
57 nT).
The observation data
show that the
duration of the magnetopause structure connected with the
negative spike in
magnetic field
and the positive spike in plasma pressure is approximately
1.5 min. If we
use, after
Phan et al. [1994],
the average
low-shear
magnetopause normal velocity of
11 km s
-1, this duration
translates into a
thickness of
0.15 RE ( RE=6.4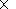 106 m).
This value may be considered only as an upper
limit. As
Phan et al. [1994] mention,
this is
due to the fact that the magnetopause is unlikely to move
unidirectionally
at the same speed. If we assume the magnetopause to be
stationary for
1.5 min if the typical satellite velocity of
2 km s
-1 is used, the
1.5 -min duration translates into a thickness of
180 km,
which may be
considered as a lower limit
[Phan et al., 1994].
According to our model of the magnetopause structure, the distance
between two current magnetopause layers is of the order of
r msh + r
msph
106 m).
This value may be considered only as an upper
limit. As
Phan et al. [1994] mention,
this is
due to the fact that the magnetopause is unlikely to move
unidirectionally
at the same speed. If we assume the magnetopause to be
stationary for
1.5 min if the typical satellite velocity of
2 km s
-1 is used, the
1.5 -min duration translates into a thickness of
180 km,
which may be
considered as a lower limit
[Phan et al., 1994].
According to our model of the magnetopause structure, the distance
between two current magnetopause layers is of the order of
r msh + r
msph 138 km
(consequently, the
thickness of the magnetopause is
138 km
(consequently, the
thickness of the magnetopause is
 276 km).
276 km).
Another example of low-shear ( < 15o) dayside magnetopause
crossing is also published in
Phan et al. [1994]
and presented in their Figures 2 and 3. On 24 October 1985
at 1302:47 UT, AMTE/IRM reached magnetopause. For the
magnetosheath
parameters,
n msh 10 cm-3,
T msh
10 cm-3,
T msh  3
3 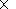 106 K,
B msh
106 K,
B msh  67 nT, we obtain:
V msh
67 nT, we obtain:
V msh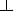
 160 km s
-1,
r msh
160 km s
-1,
r msh 36 km,
j mshy
36 km,
j mshy  1.1
1.1 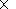 10-7 A m
-2,
and
J msh
10-7 A m
-2,
and
J msh  1.3
1.3 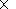 10-2 A m
-1.
10-2 A m
-1.
Respectively, for the magnetospheric parameters,
n msph  1 cm-3,
T msph
1 cm-3,
T msph  20
20 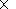 106 K,
B msph
106 K,
B msph  69 nT, we calculate:
V msph
69 nT, we calculate:
V msph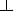
 400 km s
-1,
r msph
400 km s
-1,
r msph  93 km,
j msphy
93 km,
j msphy  -0.3
-0.3 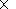 10-7 A m
-2,
J msph
10-7 A m
-2,
J msph  -0.9
-0.9 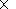 10-2 A m
-1.
The "background" magnetic field
-B0=68 nT,
and the minimum magnetic field
at the magnetopause, between two current layers, is
Bz min=61 nT.
The observed minimum magnetic field strength is of the order
of
60 nT.
The
duration of examined structure is
2 min. So, its thickness is
10-2 A m
-1.
The "background" magnetic field
-B0=68 nT,
and the minimum magnetic field
at the magnetopause, between two current layers, is
Bz min=61 nT.
The observed minimum magnetic field strength is of the order
of
60 nT.
The
duration of examined structure is
2 min. So, its thickness is
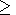 240 km, and the model
thickness of the magnetopause is
240 km, and the model
thickness of the magnetopause is
 258 km.
258 km.
For comparison, characteristic values of the
y component of the
magnetosheath and magnetospheric ion current densities calculated by
Lee and Kan [1979a]
and presented in their
Figures 2-4,
are, respectively:
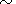 0.28
0.28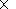 10
-7 A m
-2 and
10
-7 A m
-2 and
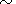 0.09
0.09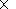 10-7 A m
-2 for
Bz msh
10-7 A m
-2 for
Bz msh 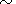 18 nT,
Bz msph
18 nT,
Bz msph 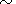 35 nT,
n msh ~18 cm
-3,
n msph ~4.5 cm
-3,
T msh ~0.3 keV,
T+ msph
35 nT,
n msh ~18 cm
-3,
n msph ~4.5 cm
-3,
T msh ~0.3 keV,
T+ msph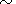 0.4 keV.
On average, electron current densities are less than the ion
densities.
0.4 keV.
On average, electron current densities are less than the ion
densities.
Our estimation of the magnetopause current layer thickness
2(r msh + r
msph) is in good agreement with the
Eastman et al. [1996]
result that the inferred
magnetopause thickness in units of plasma ion gyroradii ranges from
1.4 to 3.4, and with the
Le and Russell [1994]
conclusion that magnetopause current thickness is 2-4
ion gyroradii.
The results of our model and
observations
[e.g.,
Eastman et al., 1996;
Le and Russell, 1994]
show
that the magnetic field rotation
is connected with the ion currents.
The scale length of the
magnetopause current layer is determined by the distribution
of protons
(and positive ions) of the magnetosheath and magnetospheric
plasmas at
the boundary between them.
As mentioned above
(see
Sestero [1966]),
the
solution
obtained
satisfying the same conditions at infinity, is not unique.
Such
solutions depend on an assigned distribution function.
However, all integral characteristics of the constructed double-layer
current structure are determined unambiguously from the equilibrium
conditions.
In the
model
presented, by gyroradius we mean the Larmor radius
of an ion of energy
equal to the mean thermal energy, in the magnetic field, equal to the
arithmetic mean between the magnetic fields at the two ends of
corresponding
current
sheet at the outer space.
We constructed a model
describing the interaction
between the magnetosheath and magnetospheric plasmas at the subsolar
magnetopause for
northward IMF.
This model
is physically realistic,
gives a good representation of observations, and at the same time
is rather
simple mathematically.
9. Conclusions
The investigation of an interpenetration at the subsolar
magnetospheric
boundary of the two sorts of collisionless plasmas in a strong
magnetic field allows us to construct a model of the magnetopause
current
structure and to obtain the following results:
1. The subsolar magnetopause consists of the two current sheets
created by the magnetosheath and magnetospheric
ions.
Ion double-current layer is connected with the magnetic field
rotation.
For southward IMF, both ion currents flow from noon to dusk. This
is a
metastable configuration in which reconnection may occur.
For northward IMF,
the current created by the magnetosheath ions is
directed to dusk, and the current generated by the magnetospheric
ions
flows to dawn.
2. At the magnetopause, an interpenetration of both plasma species
exists
in the range ( -2r msh,
2r msph ).
A mechanism of generation of two double-current layers at
the subsolar magnetopause is connected with the
difference of plasma parameters and magnetic fields in the
magnetosheath and magnetosphere.
In the steady-state case,
the distance between the two ion
current sheets responsible for the magnetic field rotation
is of the order of
D mp/2 (r
msh+r msph).
Here,
r msh ( r msph ) is
the gyroradius of the thermal magnetosheath (magnetospheric) ion,
penetrating into the outer space, in the magnetic field equal
to the arithmetic mean of the fields at the
edges of the magnetosheath (magnetospheric) current layer.
(r
msh+r msph).
Here,
r msh ( r msph ) is
the gyroradius of the thermal magnetosheath (magnetospheric) ion,
penetrating into the outer space, in the magnetic field equal
to the arithmetic mean of the fields at the
edges of the magnetosheath (magnetospheric) current layer.
3. The direction of charged particle gyration at the
magnetopause is such that the magnetic field generated by each
boundary
current creates a diamagnetic effect.
4. At the subsolar magnetopause, between two ion current
sheet the strengths of the magnetic field ( B ) and its
z component
( Bz ) decrease and the plasma pressure increases. For
this
reason,
the magnetopause current region may be identified even for
northward IMF,
when the magnitudes and directions of the magnetospheric and
magnetosheath
magnetic fields are rather similar.
The main restrictions of the
model
presented
are the lack of
electrostatic field
effects and self-consistency; the initial
assumption of the
zero-width boundary between two external magnetic fields is
not in agreement
with
the thickness of the double current sheet
structure
that is obtained.
Acknowledgments
This work was supported partly by NSF Grant ATM-9801941
and RFBR Grant 98-05-64784.
V. B. Lyatsky and I. I. Alexeev provided valuable
discussions.
References
Alexeev, I. I., and E. S. Belenkaya, The structure of
convection in the
magnetosphere for a southern and northern direction of the IMF,
Geomagn. Aeron. (in Russian), 29, 640, 1989.
Belenkaya, E. S., Reconnection modes for near-radial IMF,
J. Geophys. Res., 103, 26,487, 1998a.
Belenkaya, E. S., High-latitude ionospheric convection patterns
dependent on the variable IMF orientation,
J. Atmos. Solar-Terr. Phys., 60 (13), 1343, 1998b.
Belenkaya, E. S., The current sheet structure at the
low-latitude dayside
magnetopause for different IMF directions,
Geomagn. Aeron. (in Russian), 38, 40, 1998c.
Berchem, J., and H. Okuda,
A two-dimensional particle simulation of the
magnetopause current layer,
J. Geophys. Res., 95, 8133,
1990.
Berchem, J., and C. T. Russell, The thickness of the
magnetopause current layer: ISEE 1 and 2 observations,
J. Geophys. Res., 87, 2108,
1982a.
Berchem, J., and C. T. Russell, Magnetic field rotation through
the magnetopause: ISEE 1 and 2 observations,
J. Geophys. Res., 87, 8139,
1982b.
Cargill, P. J., Hybrid simulations of tangential discontinuities,
J. Geophys. Res., 17, 1037,
1990.
Chapman, S., and V. C. A. Ferraro,
A new theory of magnetic storms,
Terr. Magn. Atmos. Elect., 36, 77,
1931a.
Chapman, S., and V. C. A. Ferraro,
A new theory of magnetic storms,
Terr. Magn. Atmos. Elect., 36, 171,
1931b.
Chapman, S., and V. C. A. Ferraro,
A new theory of magnetic storms,
Terr. Magn. Atmos. Elect., 37, 147,
1932.
Chapman, S., and V. C. A. Ferraro,
A new theory of magnetic storms,
Terr. Magn. Atmos. Elect., 38, 79,
1933.
Chapman, S., and V. C. A. Ferraro,
A new theory of magnetic storms,
Terr. Magn. Atmos. Elect., 45, 245,
1940.
De Keyser, J., and M. Roth, Equilibrium conditions for the
tangential discontinuity magnetopause,
J. Geophys. Res., 102 (A5), 9513, 1997.
Eastman, T. E., and E. W. Hones, Jr.,
Characteristics of the magnetospheric boundary layer and
magnetopause layer as observed by IMP 6,
J. Geophys. Res., 84, 2019,
1979.
Eastman, T. E., S. A. Fuselier, and J. T. Gosling, Magnetopause
crossings without a boundary layer,
J. Geophys. Res., 101, 49, 1996.
Le, G., and C. T. Russell,
The thickness and structure of high beta
magnetopause current layer,
Geophys. Res. Lett., 21, 2451,
1994.
Le, G., C. T. Russell, and J. T. Gosling, Structure of the
magnetopause for low Mach number and strongly northward
interplanetary
magnetic field,
J. Geophys. Res., 99, 23,723, 1994.
Lee, L. C., and J. R. Kan,
A unified kinetic model of the tangential magnetopause structure,
J. Geophys. Res., 84, 6417,
1979a.
Lee, L. C., and J. R. Kan,
Transition layer between two magnetized plasmas,
J. Plasma Phys., 22, part 3, 515,
1979b.
Lin, Y., and L. C. Lee, Structure of the
dayside reconnection layer in resistive MHD and hybrid models,
J. Geophys. Res., 98, 3919,
1993.
Mitchell, D. G., F. Kutchko, D. J. Williams, T. E. Eastman,
L. A. Frank, and C. T. Russell, An extended study of the
low-latitude
boundary layer on the dawn and dusk flanks of the magnetosphere,
J. Geophys. Res., 92, 7394, 1987.
Omidi, N., and D. Winske, Structure of the magnetopause inferred from
one-dimensional hybrid simulations,
J. Geophys. Res., 100, 11,935,
1995.
Paschmann, G., N. Sckopke, G. Haerendel, J. Papamastorakis,
S. J. Bame, J. R. Asbridge, J. T. Gosling,
E. W. Hones, Jr., and
E. R. Tech,
ISEE plasma observations near the subsolar magnetopause,
Space Sci. Rev., 22, 717, 1978.
Paschmann, G., W. Baumjohann, N. Sckopke, T.-D. Phan, and
M. Lühr, Structure of the dayside magnetopause
for low magnetic
shear,
J. Geophys. Res., 98, 13,409, 1993.
Phan, T.-D., and G. Paschmann, The magnetosheath region
adjacent to
the dayside magnetopause,
in
Physics of the Magnetopause, Geophys. Monogr. Ser., vol. 90,
edited by P. Song, B. U. Ö. Sonnerup,
and M. F. Thomsen,
pp. 115-122, AGU, Washington, D.C., 1995.
Phan, T.-D., and G. Paschmann, Low-latitude dayside
magnetopause and boundary layer for high
magnetic shear: 1. Structure and
motion,
J. Geophys. Res., 101, 7801, 1996.
Phan, T.-D., G. Paschmann, W. Baumjohann, N. Sckopke, and
M. Lühr, The magnetosheath region adjacent
to the
dayside magnetopause: AMPTE/IRM observations,
J. Geophys. Res., 99, 121, 1994.
Phan, T.-D., G. Paschmann, and B. U. Ö.
Sonnerup,
Low-latitude dayside
magnetopause and boundary layer for high magnetic shear:
2. Occurrence of magnetic reconnection,
J. Geophys. Res., 101, 7807, 1996.
Pudovkin, M. I., V. S. Semenov,
H. K. Biernat, C. A. Bachmaier, and M. T. Kiendl,
Structure of the subsolar magnetopause on
November 1, 1978, 1510-1530 UT: An
effect of reconnection?,
J. Geophys. Res., 100, 19,239,
1995.
Roth, M.,
The plasmapause as a plasma sheath: A minimum thickness,
J. Atmos. Terr. Phys., 38, 1065,
1976.
Roth, M., Structure of tangential discontinuities
at the magnetopause:
The nose of the magnetopause,
J. Atmos. Terr. Phys., 40, 323, 1978.
Roth, M.,
A microscopic description of interpenetrated plasma regions,
in
Proceedings of Conference on Magnetospheric Boundary Layers, ESA SP-148,
edited by B. Battrick
and J. Mort, European Space Research and Technology, Noordwijk, The
Netherlands, 1979.
Roth, M.,
J. De Keyser, and M. M. Kuznetsova,
Vlasov theory
of the equilibrium structure of tangential discontinuities
in space plasmas,
Space Sci. Rev., 76, 251,
1996.
Russell, C. T., The structure of the magnetopause,
in
Physics of the Magnetopause, Geophys. Monogr. Ser., vol. 90,
edited by P. Song, B. U. O. Sonnerup,
and M. F. Thomsen, pp. 81-98, AGU,
Washington, D.C., 1995.
Sestero, A., Structure of plasma sheets,
The Physics of Fluids, 7, 44,
1964.
Sestero, A., Vlasov equation study of plasma motion across
magnetic fields,
The Physics of Fluids, 9, 2006,
1966.
Song, P., R. C. Elphic, C. T. Russell, J. T. Gosling, and
C. A. Cattell, Structure and properties of the subsolar
magnetopause for northward IMF: ISEE observations,
J. Geophys. Res., 95, 6375, 1990.
Song, P., C. T. Russell, R. J. Fitzenreiter,
J. T. Gosling, M. F. Tomsen, D. G. Mitchell, S. A. Fuselier,
G. K. Parks, R. R. Anderson, and D. Hubert,
Structure and properties of the subsolar
magnetopause for northward
interplanetary magnetic field: Multiple-instrument particle
observations,
J. Geophys. Res., 98, 11,319,
1993.
Sonnerup, B. U. Ö., G. Paschmann, I. Papamastorakis,
G. Haerendel, S. J. Bame, J. R. Asbridge,
J. T. Gosling, and C. T. Russell,
Evidence for magnetic field reconnection at the Earth's magnetopause,
J. Geophys. Res., 86, 10,049,
1981.
Van Allen, J. A., and J. Adnan, Observed currents on the Earth's
high-latitude magnetopause,
J. Geophys. Res., 97, 6381, 1992.
Whipple, E. C., J. R. Hill, and J. D. Nichols,
Magnetopause structure and the question of particle accessibility,
J. Geophys. Res., 89, 1508,
1984.
Winglee, R. M., Non-MHD influences on the magnetospheric current
system,
J. Geophys. Res., 99, 13,437, 1994.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on December 8, 2002.
 0.03
RE.
Eastman et al. [1996]
noted that the overall
magnetopause current layer is one or a few ion gyroradii in
thickness.
Berchem and Russell [1982a]
wrote that the
parameters typical
of experimental particles and magnetic field measurements
[Paschmann et al., 1978]
give a predicted
gyroradius or
"magnetopause thickness" of between close to 1 and 100 km for
106 K electrons and
107 K protons in a 40 nT average magnetic field.
0.03
RE.
Eastman et al. [1996]
noted that the overall
magnetopause current layer is one or a few ion gyroradii in
thickness.
Berchem and Russell [1982a]
wrote that the
parameters typical
of experimental particles and magnetic field measurements
[Paschmann et al., 1978]
give a predicted
gyroradius or
"magnetopause thickness" of between close to 1 and 100 km for
106 K electrons and
107 K protons in a 40 nT average magnetic field.
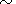 90o) through the
magnetopause
in the
(y,z) plane.
To describe the fact that charged particles from one side cannot
penetrate
arbitrarily deep into the other side, a cut-off factor is required
in the
distribution function (for example, an error function
of momenta, or a step function).
Lee and Kan [
90o) through the
magnetopause
in the
(y,z) plane.
To describe the fact that charged particles from one side cannot
penetrate
arbitrarily deep into the other side, a cut-off factor is required
in the
distribution function (for example, an error function
of momenta, or a step function).
Lee and Kan [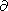 B/
B/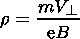
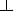 is a component of particle
velocity
perpendicular to
the magnetic field lines.
Let us briefly examine what happens at the boundary between two
different sorts of plasmas for
antiparallel
and parallel
magnetic fields.
We assume
in the first approximation that the
magnetic field boundary can be treated as a
discontinuous jump in the magnetic field
at
x=0 (at the magnetopause).
At this boundary, the density of each sort of ions penetrating
the
opposite region begins to decrease. It is postulated that
the characteristic temperature of the penetrated
particles does not change. The penetration
is limited by the ion Larmor diameter
in the magnetic field of the opposite domain.
is a component of particle
velocity
perpendicular to
the magnetic field lines.
Let us briefly examine what happens at the boundary between two
different sorts of plasmas for
antiparallel
and parallel
magnetic fields.
We assume
in the first approximation that the
magnetic field boundary can be treated as a
discontinuous jump in the magnetic field
at
x=0 (at the magnetopause).
At this boundary, the density of each sort of ions penetrating
the
opposite region begins to decrease. It is postulated that
the characteristic temperature of the penetrated
particles does not change. The penetration
is limited by the ion Larmor diameter
in the magnetic field of the opposite domain.
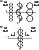
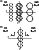
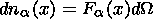
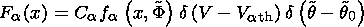

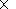 10-23 kg m
2 s
-2 is the Boltzmann constant;
Ca is a constant appropriate
to the prescribed boundary
conditions.
The cut-off function,
fa(x,F),
represents the fact that the ions from
one side cannot penetrate arbitrarily deep into the other side.
10-23 kg m
2 s
-2 is the Boltzmann constant;
Ca is a constant appropriate
to the prescribed boundary
conditions.
The cut-off function,
fa(x,F),
represents the fact that the ions from
one side cannot penetrate arbitrarily deep into the other side.


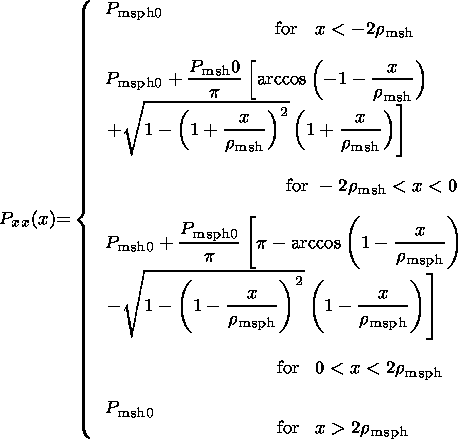

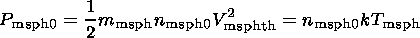
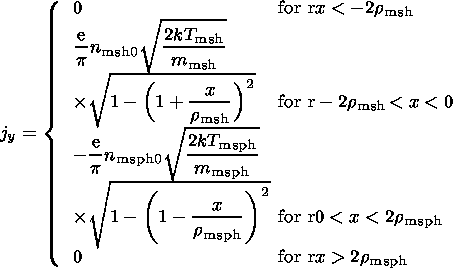
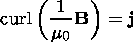
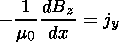

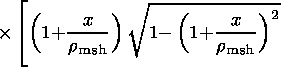
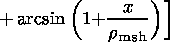
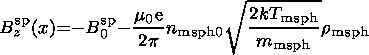
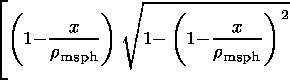
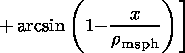
 and to
+
and to
+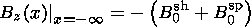
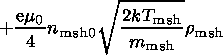
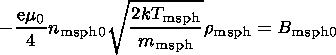
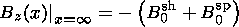
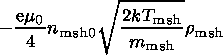
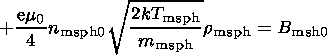
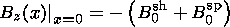
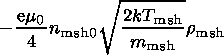

 B0
sh+B0 sp,
r msh, and
r msph --
can be found.
Quantity
.Bz(x)x=0 can be defined from the
equilibrium condition
for each current sheet boundary.
For the existence of the described current structure, the pressure
balance
must be fulfilled at the edges of each current layer:
B0
sh+B0 sp,
r msh, and
r msph --
can be found.
Quantity
.Bz(x)x=0 can be defined from the
equilibrium condition
for each current sheet boundary.
For the existence of the described current structure, the pressure
balance
must be fulfilled at the edges of each current layer:

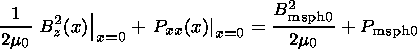
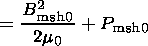

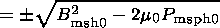
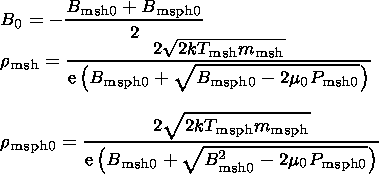
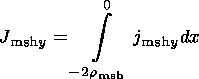
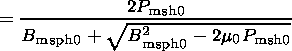
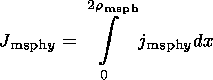
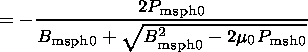
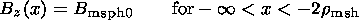
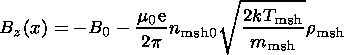
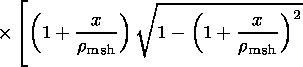
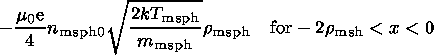
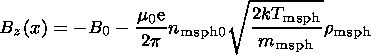
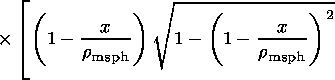
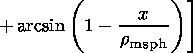
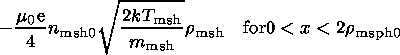
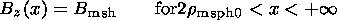
 240 km, and the model
thickness of the magnetopause is
240 km, and the model
thickness of the magnetopause is