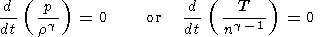
M. I. Pudovkin and S. A. Zaitseva
Physics Research Institute, St. Petersburg State University, St. Petersburg, Russia
C.-V. Meister
Astrophysikalisches Institut Potsdam, Potsdam, Germany
B. P. Besser
Institut für Weltraumforschung, Österreichische Akademie der Wissenschaften, Graz, Austria
 (x) and
T
(x) and
T (x) obtained are
used to estimate
variations of the polytropic indices
g
(x) obtained are
used to estimate
variations of the polytropic indices
g and
g
and
g across the magnetosheath.
Experimental profiles of
T
across the magnetosheath.
Experimental profiles of
T (x) and
T
(x) and
T (x) are known to
essentially
differ from the adiabatic ones. This fact may be explained by relatively intensive
energy transfer between the parallel and the perpendicular degrees of freedom.
The influence of the energy transfer between
the perpendicular and the parallel proton
temperatures on the temperature and adiabatic index profiles across the
magnetosheath is discussed, and a method of estimating the characteristic
time ( t ) of the proton temperature anisotropy relaxation
is proposed.
The relaxation time
t obtained from
T
(x) are known to
essentially
differ from the adiabatic ones. This fact may be explained by relatively intensive
energy transfer between the parallel and the perpendicular degrees of freedom.
The influence of the energy transfer between
the perpendicular and the parallel proton
temperatures on the temperature and adiabatic index profiles across the
magnetosheath is discussed, and a method of estimating the characteristic
time ( t ) of the proton temperature anisotropy relaxation
is proposed.
The relaxation time
t obtained from
T profiles
( t
profiles
( t )
is shown to be systematically greater than that obtained
from
T
)
is shown to be systematically greater than that obtained
from
T profiles ( t
profiles ( t ),
which suggests existence of some
sinks of the perpendicular proton energy.
It is shown that in spite of a rather complicated variation of
g
),
which suggests existence of some
sinks of the perpendicular proton energy.
It is shown that in spite of a rather complicated variation of
g and
g
and
g across the sheath, the
effective polytropic index
geff estimated for the entire magnetosheath
is 1.6-1.7.
across the sheath, the
effective polytropic index
geff estimated for the entire magnetosheath
is 1.6-1.7.
In the thermodynamics of gases and isotropic plasmas the relationship between variations of the gas pressure p (or temperature T ) and density for adiabatic processes is determined by the expressions
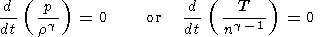 | (1) |
where r and n are plasma mass and number densities, g=cp/cv is the adiabatic index, and g=5/3 for ideal one-atomic gases. Besides thermodynamic quantities the value of g determines also some characteristics of the gas flow, such as the standoff distances of the bow shock in front of obstacles, as well as the jump of plasma parameters across the shock. This has provoked physicists to try to estimate the value of g in the solar wind plasma from corresponding experimental data [Fairfield, 1971; Farris et al., 1991; Peredo et al., 1995; Slavin et al., 1983; Zhuang and Russell, 1981]. However, results of these estimates proved to be rather contradictory and sometimes even absurd (see a short review of the problem presented by Pudovkin et al. [1997]). On the other hand, it is known that the magnetized solar wind plasma is essentially anisotropic, and the value of g obtained for it from (1) being valid for an isotropic plasma, in an anisotropic plasma, represents only some empirical relationship between the total proton (or electron) temperature and the plasma number density variations, and so it may be considered as a formal or effective adiabatic index geff.
It seems evident that in a general case,
geff is not equal to the ratio of the
specific
heats
cp/cv, and its relationship to
plasma
temperature
( T , T
, T )
component
variations and to flow characteristics is not clear.
)
component
variations and to flow characteristics is not clear.
Using the double-adiabatic laws,
Pudovkin et al. [1997]
obtained recently a general
expression for the effective adiabatic index
geff in a convecting
anisotropic collisionless plasma.
In their analysis,
geff was defined as an index which
characterizes the relationship
between the total proton temperature ( T=(T + 2 T
+ 2 T )/3 )
and plasma number density ( n ) variations expressed in the form of (1).
In particular, they showed that the
anomalous value of
geff<1, which seems to occur in the
vicinity
of the
magnetopause
[Pudovkin et al., 1995a, 1995b]
may be explained by
peculiarities of a magnetized plasma compression. However,
in their analysis the authors assumed that
the transfer between the perpendicular and
the parallel (with respect to the magnetic field
B ) components
of the temperature is negligible.
)/3 )
and plasma number density ( n ) variations expressed in the form of (1).
In particular, they showed that the
anomalous value of
geff<1, which seems to occur in the
vicinity
of the
magnetopause
[Pudovkin et al., 1995a, 1995b]
may be explained by
peculiarities of a magnetized plasma compression. However,
in their analysis the authors assumed that
the transfer between the perpendicular and
the parallel (with respect to the magnetic field
B ) components
of the temperature is negligible.
At the same time, a detailed analysis of the experimental data carried out by Denton et al. [1994] and Hill et al. [1995] has shown that such a transfer does exist and seems to be rather effective, at least in the magnetosheath regions adjacent to the magnetopause. Then there arises a problem on the applicability of the above mentioned model to studies of the real magnetosheath plasma.
Besides, an effective transfer between the perpendicular and parallel
proton temperatures
has to change significantly the relationship of the proton temperature
( Tp ) and its
component
T and
T
and
T variations to variations
of the
plasma density and hence the values of
g
variations to variations
of the
plasma density and hence the values of
g ,
g
,
g ,
and
geff. In this connection
the results of
Hau [1996]
and
Hau et al. [1993]
are
of a great interest.
They used the data from the AMPTE/IRM spacecraft for 29 magnetosheath
crossings and obtained the values of
g
,
and
geff. In this connection
the results of
Hau [1996]
and
Hau et al. [1993]
are
of a great interest.
They used the data from the AMPTE/IRM spacecraft for 29 magnetosheath
crossings and obtained the values of
g =0.94
=0.94
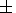 0.1 and
g
0.1 and
g = 1.14
= 1.14 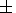 0.13 for the entire magnetosheath. These
relatively low values of
g
0.13 for the entire magnetosheath. These
relatively low values of
g and
g
and
g were explained by them in terms of
nonadiabatic effects. On the other
hand, the same experimental profiles of
T
were explained by them in terms of
nonadiabatic effects. On the other
hand, the same experimental profiles of
T and
T
and
T were explained
by
Denton et al. [1994]
and
Hill et al. [1995]
by an effective
energy transfer from
T
were explained
by
Denton et al. [1994]
and
Hill et al. [1995]
by an effective
energy transfer from
T to
T
to
T .
.
In this paper we consider in detail characteristics of the
magnetosheath plasma
flow in the vicinity of the subsolar streamline predicted by the model
[Pudovkin and Lebedeva, 1987;
Pudovkin et al., 1995a, 1995b].
The aim of the consideration is
to estimate expected values of the
polytropic indices
g ,
g
,
g ,
and
geff and their variations across
the magnetosheath for an
adiabatic flow. Special attention is paid to the influence
of the proton
pitch-angle diffusion on the expected values of
g
,
and
geff and their variations across
the magnetosheath for an
adiabatic flow. Special attention is paid to the influence
of the proton
pitch-angle diffusion on the expected values of
g ,
g
,
g ,
and
geff. The results obtained will be used
for
the interpretation of
experimental data, and some conclusions
will be drawn
on to what degree the
magnetosheath plasma flow is adiabatic.
Also,
the characteristic time of relaxation of the proton temperature
anisotropy ( t )
will be estimated.
,
and
geff. The results obtained will be used
for
the interpretation of
experimental data, and some conclusions
will be drawn
on to what degree the
magnetosheath plasma flow is adiabatic.
Also,
the characteristic time of relaxation of the proton temperature
anisotropy ( t )
will be estimated.
In the analysis below we shall suppose that the temperature anisotropy
in the
convecting collisionless plasma arises due to the splitting of
the parallel and perpendicular
(with respect to the magnetic field) degrees of freedom and, as a result,
to independent
heating or cooling of the plasma in these two directions.
Variations of the perpendicular and parallel pressures ( p and
p
and
p , respectively)
and of corresponding components of the plasma temperature
( T
, respectively)
and of corresponding components of the plasma temperature
( T and
T
and
T ) are given by three
sets of equations.
The double-adiabatic equations which may be obtained from the
conservation
of two adiabatic invariants:
m=
) are given by three
sets of equations.
The double-adiabatic equations which may be obtained from the
conservation
of two adiabatic invariants:
m=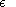
 /B,
and
I=
/B,
and
I=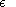

 l2, where
l is the length of the "fluid'' segment of a field line
[Chew et al., 1956]:
l2, where
l is the length of the "fluid'' segment of a field line
[Chew et al., 1956]:
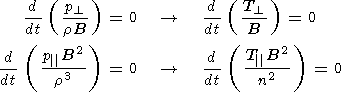 | (2) (3) |
The continuity equation
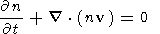 | (4) |
where v is the plasma velocity. And the frozen-in magnetic field equation
 | (5) |
Using (2)-(5), we can obtain the values of the adiabatic indices as [Belmont and Mazelle, 1992; Pudovkin et al., 1995a, 1995b]:
 | (6) (7) |
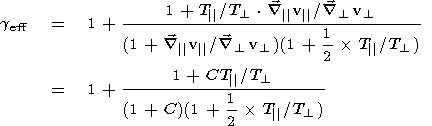 | (8) |
Here
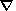

 v
v =
=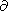 vz/
vz/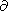 z and
z and
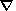

 v
v =
= 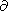 vx /
vx / 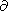 x +
x + 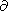 vy
/
vy
/ 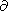 y are calculated in a local Cartesian
coordinate system with the
Z axis
directed along
the magnetic field line at the point of observation (or calculation),
and
X and
Y axes
lying in the plane perpendicular to the local
B.
C=
y are calculated in a local Cartesian
coordinate system with the
Z axis
directed along
the magnetic field line at the point of observation (or calculation),
and
X and
Y axes
lying in the plane perpendicular to the local
B.
C= 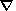

 v
v /
/ 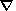

 v
v is a modification of the well-known parameter of
the magnetic
compressibility ( C=Cp-1, where
Cp is the magnetic compression index
[Belmont and Mazelle, 1992])
introduced to distinguish more obviously
between the flows
in which the plasma compression along the magnetic field is
associated with the plasma
compression or decompression in the perpendicular direction.
In particular, while analyzing
the plasma flow within the magnetosheath, we suppose that the plasma
moving earthward
along the subsolar stream line is compressed in the direction
perpendicular to the magnetic
field (
is a modification of the well-known parameter of
the magnetic
compressibility ( C=Cp-1, where
Cp is the magnetic compression index
[Belmont and Mazelle, 1992])
introduced to distinguish more obviously
between the flows
in which the plasma compression along the magnetic field is
associated with the plasma
compression or decompression in the perpendicular direction.
In particular, while analyzing
the plasma flow within the magnetosheath, we suppose that the plasma
moving earthward
along the subsolar stream line is compressed in the direction
perpendicular to the magnetic
field ( 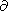 vx/
vx/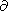 x < 0 ). Thus
C<0 corresponds to
x < 0 ). Thus
C<0 corresponds to
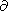 vz/
vz/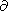 z>0,
i.e., to plasma
spreading from the subsolar streamline, and
C>0 corresponds to the flow
with streamlines converging to the subsolar line.
z>0,
i.e., to plasma
spreading from the subsolar streamline, and
C>0 corresponds to the flow
with streamlines converging to the subsolar line.
It should be noted that contrary to the generally accepted point of view,
formulae (6)
and (7) result in
g =2
only for pure perpendicular
compression of the plasma ( C=0 ), and
g
=2
only for pure perpendicular
compression of the plasma ( C=0 ), and
g differs from 2
for any oblique compression. Respectively, one has
g
differs from 2
for any oblique compression. Respectively, one has
g =3
only for a pure parallel compression, and in
any other case,
g
=3
only for a pure parallel compression, and in
any other case,
g
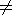 3. Thus a deviation of
g
3. Thus a deviation of
g and
g
and
g indices from their "canonical'' values does not
necessarily mean that the plasma flow is nonadiabatic.
indices from their "canonical'' values does not
necessarily mean that the plasma flow is nonadiabatic.
The value and gradients of the plasma velocity are determined by
the equation of motion. However,
to make the results of the model profile analysis
comparable with those of experimental profiles (see below),
we shall express ( 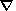
 v ),
(
v ),
( 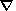

 v
v ),
and
(
),
and
( 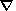

 v
v )
in terms of gradients of the magnetic field intensity and plasma density:
)
in terms of gradients of the magnetic field intensity and plasma density:
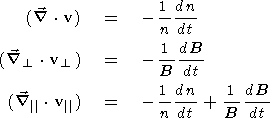 | (9) (10) (11) |
As for the temperature profiles, they are easily obtained from (2) and (3) as
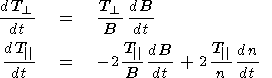 | (12) (13) |
The proton pitch-angle diffusion will be taken into account by introducing into the right-hand sides of (11) and (12) the relaxation terms (the so-called t approximation) in the form [see Denton et al., 1994; Hesse and Birn, 1992; Pudovkin and Smolin, 1988; Shishkina et al., 1995]
 |
where Teq is an equilibrium temperature, and t is the temperature anisotropy relaxation time. Then equations (12) and (13) may be rewritten in the form
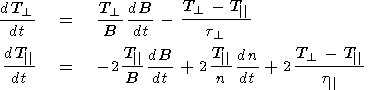 | (14) (15) |
Provided the plasma flow is constant in time, so that we can replace
d/dt by
v  d/dx, we have
d/dx, we have
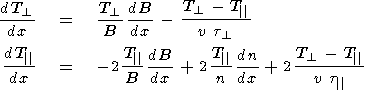 | (16) (17) |
Having inverted (16) and (17), one may obtain expressions which allow one to estimate the values of t from observed profiles of the magnetosheath plasma parameters:
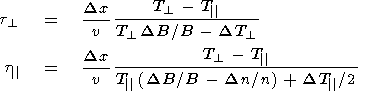 | (18) (19) |
where
DB and
DT are the differences of
B and
T over the
spatial interval
Dx. In the case of an adiabatic flow the
values
of
t, determined from the variations of
T and
T
and
T ,
which we refer to as
t
,
which we refer to as
t and
t
and
t ,
respectively,
have to coincide, since in this case there is no input or output of energy to
(from) the plasma, and the energy lost by the transversal motion of protons
has to be transferred to the energy of
their longitudinal motion (the thermal energy
of the magnetosheath electrons is small
[Phan et al., 1994]
and may
be neglected).
,
respectively,
have to coincide, since in this case there is no input or output of energy to
(from) the plasma, and the energy lost by the transversal motion of protons
has to be transferred to the energy of
their longitudinal motion (the thermal energy
of the magnetosheath electrons is small
[Phan et al., 1994]
and may
be neglected).
Using this model, we shall analyze the variations of the plasma parameters across the magnetosheath to investigate possible influence of the pitch-angle diffusion on the proton temperature anisotropy and values of the adiabatic indices and to estimate the temperature anisotropy relaxation time t.
Analyzing the observed variations of the plasma parameters across the magnetosheath, one has to bear in mind that in the presence of the magnetic field reconnection at the magnetopause resulting in a nonzero normal component of the velocity vn=(0.1-0.2)va [Feldman, 1986] ( va is the Alfvén velocity), it takes about 10-20 min for the solar wind plasma to cross the magnetosheath along the subsolar streamline and, on average, about 2 hours for a spacecraft. Correspondingly, in order to consider a crossing as a "stationary'' one, solar wind parameters should preserve their values for at least 2 hours. However, we have no solar wind data during the crossings discussed by Hau et al. [1993] and by Hill et al. [1995] and therefore do not know whether this condition was fulfilled during these crossings. Even more, there are reasons to believe, as will be shown below, that the solar wind was highly fluctuating during the first of these crossings. Nevertheless, we shall consider at first a stationary model profile, for which we shall use one of the magnetosheath parameter profiles calculated using the model by Pudovkin and Lebedeva [1987] and Pudovkin et al. [1995a, 1995b].
In this model, variations of the plasma and magnetic field parameters along the subsolar streamline are calculated under the assumption that the plasma is spreading from the symmetry plane (which contains the subsolar streamline in the magnetosheath and the reconnection line at the magnetopause [see Pudovkin and Lebedeva, 1987] in the direction perpendicular to that plane.
At this point we have to note that this model was developed for an isotropic plasma with g=5/3, which apparently restricts the applicability of the model while dealing with an anisotropic plasma. As the results of numerical modeling show, n(x) and B(x) profiles calculated for the isotropic and anisotropic plasmas differ insignificantly [Pudovkin et al., 1999], which proves applicability of the isotropic model.
 With this in mind we present in Figure 1 variations of the plasma density
( n ), velocity ( v ), and magnetic field intensity ( B ) across the
magnetosheath calculated along the subsolar streamline
for
Q=150o ( Q is the angle between the solar wind
magnetic field vector projection on the
YZ plane of the GSM coordinate
system and the
Z axis of that system), Mach number
M=8,
and
Alfvénic Mach number
Ma=10.
B and
n values in the figure are
normalized using their values in the solar wind ( Bsw=4.65 nT and
nsw=5 cm
-3 ), and values of
v are normalized using the velocity
just after the bow-shock crossing ( vbs=125 km s
-1 ).
With this in mind we present in Figure 1 variations of the plasma density
( n ), velocity ( v ), and magnetic field intensity ( B ) across the
magnetosheath calculated along the subsolar streamline
for
Q=150o ( Q is the angle between the solar wind
magnetic field vector projection on the
YZ plane of the GSM coordinate
system and the
Z axis of that system), Mach number
M=8,
and
Alfvénic Mach number
Ma=10.
B and
n values in the figure are
normalized using their values in the solar wind ( Bsw=4.65 nT and
nsw=5 cm
-3 ), and values of
v are normalized using the velocity
just after the bow-shock crossing ( vbs=125 km s
-1 ).
One can see that on the whole, the model profiles of the magnetosheath parameters are similar to the experimental ones, and the model reproduces the gross features of the magnetosheath plasma flow.
In addition, we show in Figure 1 the variations of
T and
T
and
T (normalized by their
values at the bow shock, taken as
T
(normalized by their
values at the bow shock, taken as
T 0=6
0=6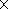 106 K and
T
106 K and
T 0=4.8
0=4.8 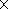 106 K)
calculated (again, in a nonself-consistent manner)
from the
B(x) and
n(x) profiles in accordance with the adiabatic equations
(2) and (3).
106 K)
calculated (again, in a nonself-consistent manner)
from the
B(x) and
n(x) profiles in accordance with the adiabatic equations
(2) and (3).
These profiles show that the drift of the magnetosheath plasma in a magnetic
field increasing on approach to the magnetopause results in an increase of
T and simultaneous decrease
of
T
and simultaneous decrease
of
T , which contradicts the
experimental data. As was said above, this contradiction was explained by
Hau et al. [1993]
by some nonadiabatic effects and by
Denton et al. [1994]
and
Hill et al. [1995]
by the pitch-angle diffusion of protons.
In the next sections we shall try to distinguish between these two effects.
, which contradicts the
experimental data. As was said above, this contradiction was explained by
Hau et al. [1993]
by some nonadiabatic effects and by
Denton et al. [1994]
and
Hill et al. [1995]
by the pitch-angle diffusion of protons.
In the next sections we shall try to distinguish between these two effects.
 For the given profiles of
B(x) and
n(x) the values of (
For the given profiles of
B(x) and
n(x) the values of ( 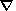
 v
v ), (
), ( 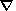
 v
v ),
and their ratio
C(x)=(
),
and their ratio
C(x)=( 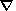
 v )/(
v )/( 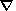
 v ) may be
calculated using (10) and (11), and
the results are presented in Figure 2.
v ) may be
calculated using (10) and (11), and
the results are presented in Figure 2.
As is seen from Figure 2, C(x) is negative throughout the magnetosheath (this corresponds to a plasma compression along the X axis and its expansion in perpendicular directions), gradually decreasing from C(x)=-0.75 near the bow shock to C(x)=-3 in the magnetopause vicinity.
This regular behavior of the C(x) index obtained for a stationary model will be compared below with experimental data to judge on the stationarity of the experimental profiles under consideration.
Values of
g and
g
and
g may be calculated from the
profiles of
T
may be calculated from the
profiles of
T ,
T
,
T ,
and
n presented in Figure 2.
Indeed, from the adiabatic laws one has
,
and
n presented in Figure 2.
Indeed, from the adiabatic laws one has
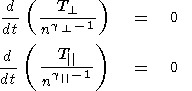 | (20) (21) |
and therefrom
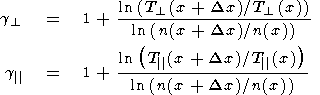 | (22) (23) |
Profiles of
g and
g
and
g obtained in this manner are
also given in Figure 2.
In spite of rather rapid
variations of
g
obtained in this manner are
also given in Figure 2.
In spite of rather rapid
variations of
g and
g
and
g the sum
Sg
(g
the sum
Sg
(g +2g
+2g )
is equal to
5 throughout the entire
magnetosheath, consistent with an adiabatic process
[Belmont and Mazelle, 1992].
)
is equal to
5 throughout the entire
magnetosheath, consistent with an adiabatic process
[Belmont and Mazelle, 1992].
 Until now, we have neglected the possible energy transfer
between parallel
and perpendicular degrees of freedom in the magnetosheath plasma. To
illustrate the influence of such a transfer, we have integrated
(using the Runge-Kutta method) the system of equations (16) and
(17) for different values of
t, and the results are presented
in Figure 3.
The curves in Figure 3 show that as should be expected, the
pitch-angle diffusion significantly alters the temperature profiles across
the magnetosheath, and when
t
Until now, we have neglected the possible energy transfer
between parallel
and perpendicular degrees of freedom in the magnetosheath plasma. To
illustrate the influence of such a transfer, we have integrated
(using the Runge-Kutta method) the system of equations (16) and
(17) for different values of
t, and the results are presented
in Figure 3.
The curves in Figure 3 show that as should be expected, the
pitch-angle diffusion significantly alters the temperature profiles across
the magnetosheath, and when
t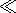 Dt
(where
Dt
Dt
(where
Dt 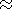 300-1000 s
is the time taken by the solar wind plasma to cross the
magnetosheath),
T
300-1000 s
is the time taken by the solar wind plasma to cross the
magnetosheath),
T and
T
and
T rapidly approach an equilibrium
state, and then vary together. In the region adjacent to the magnetopause,
both components of the proton temperature decrease, which agrees with
the experimental data by
Denton et al. [1994],
Hau [1996],
Hau et al. [1993],
and
Hill et al. [1995].
rapidly approach an equilibrium
state, and then vary together. In the region adjacent to the magnetopause,
both components of the proton temperature decrease, which agrees with
the experimental data by
Denton et al. [1994],
Hau [1996],
Hau et al. [1993],
and
Hill et al. [1995].
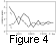 The change of
T
The change of
T (x) and
T
(x) and
T (x) profiles immediately
results
in a change of the polytropic indices
g
(x) profiles immediately
results
in a change of the polytropic indices
g and
g
and
g (see Figure 4).
In particular, in the case
t
(see Figure 4).
In particular, in the case
t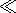 Dt
(e.g., for
t=5 s and
t=10 s),
T
Dt
(e.g., for
t=5 s and
t=10 s),
T
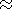 T
T and the magnetosheath
plasma
behaves like an isotropic plasma with
g
and the magnetosheath
plasma
behaves like an isotropic plasma with
g
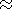 g
g
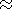 5/3.
5/3.
Thus the values of
g and
g
and
g can differ strongly
from their adiabatic values; however, this does not imply the existence of
sources or sinks of energy; all the calculations were carried out
for an adiabatic process.
can differ strongly
from their adiabatic values; however, this does not imply the existence of
sources or sinks of energy; all the calculations were carried out
for an adiabatic process.
 It seems interesting to consider the variations of
geff for given
n(x),
T
It seems interesting to consider the variations of
geff for given
n(x),
T (x),
and
T
(x),
and
T (x) profiles across
the magnetosheath
for various values of
t. In this connection we present in Figure 5
profiles of
geff, calculated as
(x) profiles across
the magnetosheath
for various values of
t. In this connection we present in Figure 5
profiles of
geff, calculated as
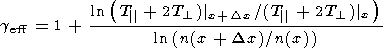 | (24) |
for
t = 5 s,
100 s, and
t
 .
One can see from Figure 5 that in the case
t= 5 s,
geff
.
One can see from Figure 5 that in the case
t= 5 s,
geff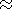 5/3 through the entire magnetosheath.
When
t=100 s,
geff varies from about
2 at the beginning of the profile
to approximately
1.5 on approach to
the magnetopause. When
t
5/3 through the entire magnetosheath.
When
t=100 s,
geff varies from about
2 at the beginning of the profile
to approximately
1.5 on approach to
the magnetopause. When
t
 ,
geff,
being greater than
2 in the outer
magnetosheath, proves to be less than unity in the inner regions of the sheath.
,
geff,
being greater than
2 in the outer
magnetosheath, proves to be less than unity in the inner regions of the sheath.
Finally, we shall consider the possibility of determining the value
of the temperature anisotropy relaxation time
t from the
T (x),
T
(x),
T (x),
B(x),
n(x),
and
v(x) profiles.
(x),
B(x),
n(x),
and
v(x) profiles.
 A solution of that problem (in connection with the proton temperature
anisotropy within the plasma sheet in the magnetotail) was proposed by
Hesse and Birn [1992],
Pudovkin and Smolin [1988], and
Shishkina et al. [1995]
on the basis of equations similar to (16) and
(17); an estimate of
t was obtained from a comparison of
calculated profiles of the temperature anisotropy with the observed ones.
Using the same equations,
Denton et al. [1994]
obtained the value of
t in the magnetosheath in the
close vicinity of the magnetopause. In their analysis,
Denton et al. [1994],
as well as
Pudovkin and Smolin [1988],
assumed the
variations of
T
A solution of that problem (in connection with the proton temperature
anisotropy within the plasma sheet in the magnetotail) was proposed by
Hesse and Birn [1992],
Pudovkin and Smolin [1988], and
Shishkina et al. [1995]
on the basis of equations similar to (16) and
(17); an estimate of
t was obtained from a comparison of
calculated profiles of the temperature anisotropy with the observed ones.
Using the same equations,
Denton et al. [1994]
obtained the value of
t in the magnetosheath in the
close vicinity of the magnetopause. In their analysis,
Denton et al. [1994],
as well as
Pudovkin and Smolin [1988],
assumed the
variations of
T and
T
and
T to be determined by the
same values of
t, which is correct only
in the case of adiabatic processes
[see
Hau, 1996;
Hau et al., 1993].
In this connection it seems useful to determine
t
to be determined by the
same values of
t, which is correct only
in the case of adiabatic processes
[see
Hau, 1996;
Hau et al., 1993].
In this connection it seems useful to determine
t and
t
and
t independently and thus to judge
to what degree the process under consideration is adiabatic. These estimates
may be obtained using equations (18) and (19). To test
the method, we used
T
independently and thus to judge
to what degree the process under consideration is adiabatic. These estimates
may be obtained using equations (18) and (19). To test
the method, we used
T (x) and
T
(x) and
T (x)
profiles calculated
for
t=50 s (see Figure 1). The results of recalculating
t
(x)
profiles calculated
for
t=50 s (see Figure 1). The results of recalculating
t (x) and
t
(x) and
t (x) from these profiles are presented in Figure 6.
One can see that
t
(x) from these profiles are presented in Figure 6.
One can see that
t and
t
and
t vary around the value
t
vary around the value
t =t
=t =
49.9
=
49.9 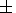 0.1,
which is rather close to the true value of
t.
0.1,
which is rather close to the true value of
t.
A more detailed analysis of the problem shows that the values of t may be obtained with reasonable accuracy when t varies in the range 0.1 Dt < t< 10 Dt, where Dt is, as earlier, the time taken by the solar wind plasma to cross the magnetosheath.
Now we shall use the model proposed above for the analysis of experimental data, in particular the magnetosheath parameter profiles presented by Hau et al. [1993] and by Hill et al. [1995] obtained onboard the AMPTE/IRM satellite. Both profiles took place in the magnetosheath in the vicinity of the subsolar streamline: the latitude of the satellite and LT varied from -4o to -3o and from 1202 to 1229, respectively, for the Hill et al. [1995] crossing and from -5.9o to -4o and 1311 to 1350, respectively, for the Hau et al. [1993] crossing. Of course, a deflection of the satellite's latitude from zero, and of its local time from 12 hours, means that the satellite trajectory does not coincide with the subsolar streamline, and this may essentially embarrass the comparison of the model and experimental data. However, we have no better data. To our regret, we had no original data for these crossings and therefore had to digitize the curves published in the journal articles. Practically, we could only obtain values of magnetosheath parameters at a few characteristic points of the profiles, and all other values were found by interpolation between these points. This is why the "experimental'' data are represented by smooth lines and do not exhibit any scatter. The values taken from the profiles are listed in Tables 1 and 2.
 First of all, we consider the character of the plasma
flow in the magnetosheath
during the crossing on November 17, 1985
[Hill et al., 1995].
Unfortunately,
we could not get hold of any data on the solar wind for this period, and
to
judge to what degree the conditions in the solar wind were (or were not)
stationary, the profile of the plasma compression parameter
C(x) was
calculated using the data given in Table 1 and formulae
(9)-(11).
The results are presented by the curves at the bottom of
Figures 7a
and 7b.
The curves show that
C(x) is negative over the entire magnetosheath and gradually varies
from
C(x)
First of all, we consider the character of the plasma
flow in the magnetosheath
during the crossing on November 17, 1985
[Hill et al., 1995].
Unfortunately,
we could not get hold of any data on the solar wind for this period, and
to
judge to what degree the conditions in the solar wind were (or were not)
stationary, the profile of the plasma compression parameter
C(x) was
calculated using the data given in Table 1 and formulae
(9)-(11).
The results are presented by the curves at the bottom of
Figures 7a
and 7b.
The curves show that
C(x) is negative over the entire magnetosheath and gradually varies
from
C(x) 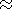 -0.8 near the bow shock
to
C(x)
-0.8 near the bow shock
to
C(x) 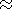 -1.5 in the magnetopause
vicinity
(a relatively rapid jump of the
C(x) value at
x
-1.5 in the magnetopause
vicinity
(a relatively rapid jump of the
C(x) value at
x 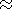 5500 km is
most probably associated with an inaccuracy in digitizing the experimental
curves). This variation is similar to the
C(x) variation
shown in Figure 2,
and the crossing on November 17, 1985 may be considered to
be in a quasi steady state regime.
This allows one to use the results of the model presented above for the
interpretation
of data of this crossing. Curves in the top part of Figure 7a show the
expected variations of
T
5500 km is
most probably associated with an inaccuracy in digitizing the experimental
curves). This variation is similar to the
C(x) variation
shown in Figure 2,
and the crossing on November 17, 1985 may be considered to
be in a quasi steady state regime.
This allows one to use the results of the model presented above for the
interpretation
of data of this crossing. Curves in the top part of Figure 7a show the
expected variations of
T calculated from the
B(x), v(x),
and
n(x) profiles according to equations (16) and (17) for various
values of
t.
Again, we have to remind here that a rapid bending of
all the curves at
X=5500 km is associated
with inaccuracy in digitizing experimental profiles
B(x) and
n(x) and by
substitution of the real smooth curves by a sequence of segments with linearly
changing variables. One can see that experimental values (also given in
Figure 7a)
are in a close agreement with the model curves
with
5 < t < 50 s,
which suggests a rather intense output of energy from transversal
degrees of freedom, supposingly, to the field-aligned ones.
calculated from the
B(x), v(x),
and
n(x) profiles according to equations (16) and (17) for various
values of
t.
Again, we have to remind here that a rapid bending of
all the curves at
X=5500 km is associated
with inaccuracy in digitizing experimental profiles
B(x) and
n(x) and by
substitution of the real smooth curves by a sequence of segments with linearly
changing variables. One can see that experimental values (also given in
Figure 7a)
are in a close agreement with the model curves
with
5 < t < 50 s,
which suggests a rather intense output of energy from transversal
degrees of freedom, supposingly, to the field-aligned ones.
However, the variations of the parallel temperature
T given in the
top part of Figure 7b seem to be more complicated.
Indeed, in the first half
of the profile the experimental curve of
T
given in the
top part of Figure 7b seem to be more complicated.
Indeed, in the first half
of the profile the experimental curve of
T almost coincides with
the model curve with
t
almost coincides with
the model curve with
t
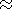 500 s, which means that the
decrease of
T
500 s, which means that the
decrease of
T proceeds almost adiabatically,
and only in the inner
part of the magnetosheath the slope of the experimental curve corresponds to
the model curves with
t
proceeds almost adiabatically,
and only in the inner
part of the magnetosheath the slope of the experimental curve corresponds to
the model curves with
t varying in the range
5-100 s.
varying in the range
5-100 s.
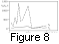 This estimate may be confirmed by the direct calculation
of
t
This estimate may be confirmed by the direct calculation
of
t and
t
and
t from the
T
from the
T (x) and
T
(x) and
T (x) profiles with
the use of formulae (18) and (19). Corresponding
values of relaxation times are presented in Figure 8, in which one can see
that in the first half of the profile,
t
(x) profiles with
the use of formulae (18) and (19). Corresponding
values of relaxation times are presented in Figure 8, in which one can see
that in the first half of the profile,
t is equal to
50-150 s, while
t
is equal to
50-150 s, while
t varies from
300 to
1300 s, and only
in the inner part of the magnetosheath it drops to 100-200 s.
This estimate is close to (though somewhat larger than) the value of
t obtained by
Denton et al. [1994]
for the flow near the magnetopause.
varies from
300 to
1300 s, and only
in the inner part of the magnetosheath it drops to 100-200 s.
This estimate is close to (though somewhat larger than) the value of
t obtained by
Denton et al. [1994]
for the flow near the magnetopause.
Thus the plasma flow in the magnetosheath in the case under consideration seems
to pass two distinctly different stages: in the outer regions of the
magnetosheath the energy transfer between the perpendicular and
the parallel temperatures is relatively small and does not play any significant
role, at least in the behavior of
T . Whereas in the inner
magnetosheath this energy transfer increases to such a degree that it affects
the variations of both
T
. Whereas in the inner
magnetosheath this energy transfer increases to such a degree that it affects
the variations of both
T and
T
and
T and causes a
significant deflection of the
T
and causes a
significant deflection of the
T (x) profile from
the adiabatic one.
(x) profile from
the adiabatic one.
Besides, it has to be noted that even in the outer magnetosheath, the rate of
the
T increase is somewhat less
than it is predicted by the adiabatic
law, which means that the transverse thermal energy is dissipated.
At the same time, as we have seen, this energy is not transferred to the
parallel temperature energy, which suggests the
existence of some other sinks of perpendicular energy (e.g., the energy may be
transmitted from protons to electrons, where the latter, due to their very high
heat conduction, move almost isothermically).
increase is somewhat less
than it is predicted by the adiabatic
law, which means that the transverse thermal energy is dissipated.
At the same time, as we have seen, this energy is not transferred to the
parallel temperature energy, which suggests the
existence of some other sinks of perpendicular energy (e.g., the energy may be
transmitted from protons to electrons, where the latter, due to their very high
heat conduction, move almost isothermically).
In the inner magnetosheath,
t is also 1.5-2 times greater than
t
is also 1.5-2 times greater than
t ; however, taking into account the low accuracy of the
experimental data, we cannot be sure of the reality of this difference.
; however, taking into account the low accuracy of the
experimental data, we cannot be sure of the reality of this difference.
What may be the cause of the change of the proton pitch-angle diffusion? It seems reasonable to suppose that it is associated with the change of the intensity of the plasma wave turbulence responsible for the proton pitch-angle scattering. Hill et al. [1995] suppose that the mirror-wave instability plays the main role in that process. This conclusion seems to be convincingly confirmed by observations of plasma density and magnetic field intensity variations identified by the authors with mirror waves and by fulfillment of the mirror-wave-instability criterion in most of the cases analyzed by them.
In this connection we present, in the bottom panels
of Figures 7a
and 7b,
curves
showing the variations of the value of
Kph=T /T
/T -(1+ 0.85 (b
-(1+ 0.85 (b )1/2 ) with
b
)1/2 ) with
b = 8 pn k T
= 8 pn k T /B2, which determines the threshold
of the development of the mirror-wave
instability
[Phan et al., 1994].
Figures 7a
and 7b
show that during the entire
crossing the value of
T
/B2, which determines the threshold
of the development of the mirror-wave
instability
[Phan et al., 1994].
Figures 7a
and 7b
show that during the entire
crossing the value of
T /T
/T is close to the instability
threshold, and an intensive proton pitch-angle diffusion starts when the
temperature anisotropy
T
is close to the instability
threshold, and an intensive proton pitch-angle diffusion starts when the
temperature anisotropy
T /T
/T exceeds the threshold value,
which seems to confirm the idea of the leading role of the mirror-wave
instability in the process under consideration. On the other hand, the
variations of the
Kph value are relatively
small,
so some doubts arise whether they really can cause such significant
changes of the rate of the pitch-angle diffusion. In this
connection
we should like to draw attention to the fact that the change of the
pitch-angle diffusion regime coincides
in time with a rather rapid increase of the plasma expansion
along the magnetic field lines, manifested
by the decrease of the
C(x) value (see Figures 7a and 7b),
which allows one to
suppose that this change in the plasma flow character, and consequently
in the rate of the
T
exceeds the threshold value,
which seems to confirm the idea of the leading role of the mirror-wave
instability in the process under consideration. On the other hand, the
variations of the
Kph value are relatively
small,
so some doubts arise whether they really can cause such significant
changes of the rate of the pitch-angle diffusion. In this
connection
we should like to draw attention to the fact that the change of the
pitch-angle diffusion regime coincides
in time with a rather rapid increase of the plasma expansion
along the magnetic field lines, manifested
by the decrease of the
C(x) value (see Figures 7a and 7b),
which allows one to
suppose that this change in the plasma flow character, and consequently
in the rate of the
T decrease,
may be responsible for the observed increase of the energy transfer rate.
The next question we should like to discuss here is the variation of the
polytropic index values across the magnetosheath.
decrease,
may be responsible for the observed increase of the energy transfer rate.
The next question we should like to discuss here is the variation of the
polytropic index values across the magnetosheath.
Expected variations of
g and
g
and
g for a flow
with
T
for a flow
with
T /T
/T
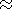 1.2-1.3 and
t
1.2-1.3 and
t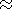 50 s
have been
discussed earlier and are shown in Figure 4. It shows that in the bulk
of the magnetosheath the
g
50 s
have been
discussed earlier and are shown in Figure 4. It shows that in the bulk
of the magnetosheath the
g and
g
and
g values are expected to vary in the range 1.5-2.
values are expected to vary in the range 1.5-2.
 The observed values of
g
The observed values of
g and
g
and
g are given
in Figure 9.
One can see in Figure 9 that the behavior
of
g
are given
in Figure 9.
One can see in Figure 9 that the behavior
of
g generally agrees with the model prediction.
At the same time, the observed variation of
g
generally agrees with the model prediction.
At the same time, the observed variation of
g drastically
differs from the expected one and is much closer to that
of an adiabatic flow (see Figure 2). This result confirms once more
the conclusion that the energy transfer from the perpendicular component
of the proton temperature to the parallel one is small in the outer regions
of the magnetosheath.
drastically
differs from the expected one and is much closer to that
of an adiabatic flow (see Figure 2). This result confirms once more
the conclusion that the energy transfer from the perpendicular component
of the proton temperature to the parallel one is small in the outer regions
of the magnetosheath.
Concerning the Sg index, one can see from Figure 9 that at the first part of the profile, it ranges between -2 and -4, which greatly differs from its adiabatic value Sg=5. This also confirms the assumption that the proton temperature in that part of the magnetosheath changes nonadiabatically.
On the other hand, within the inner layers of the magnetosheath, Sg varies around the value Sg=5, which agrees with the adiabatic model.
Beside the
g and
g
and
g profiles, Figure 9
shows also
variations of the effective adiabatic index
geff calculated using
(24). The figure shows that at the outer part of the crossing
the observed variations of
geff significantly differ from the expected
ones for both
t=50 s and
t
profiles, Figure 9
shows also
variations of the effective adiabatic index
geff calculated using
(24). The figure shows that at the outer part of the crossing
the observed variations of
geff significantly differ from the expected
ones for both
t=50 s and
t
 (see Figure 5),
which may be explained by the adiabatic decrease of
T
(see Figure 5),
which may be explained by the adiabatic decrease of
T along with the nonadiabatic
change of
T
along with the nonadiabatic
change of
T with
t
with
t
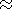 100 s.
Within the inner magnetosheath,
geff is seen to be close to the value
predicted by the model with
t=100 s.
100 s.
Within the inner magnetosheath,
geff is seen to be close to the value
predicted by the model with
t=100 s.
At the same time, it is interesting to note that the "mean" value of geff characterizing the variation of the proton temperature across the entire magnetosheath and calculated substituting into (24) the values of T and n measured at the magnetopause edge of the profile and in the vicinity of the bow shock is
 geff
geff
 = 1.7
= 1.7 This agrees with the results of Fairfield [1971], Farris et al. [1991], Peredo et al. [1995], Slavin et al. [1983], and Zhuang and Russell [1981], where g was found using such integral characteristics as the magnetosheath thickness.
 Values of the magnetosheath parameters obtained for this
crossing
were analyzed in the same manner as above.
The bottom curve in Figures 10a and 10b shows
the variation of the plasma compression index
C(x). One can see from
Figure 10a
that contrary to the previous case, the value of
C(x) at the
beginning of the profile is positive. For
a stationary flow this would mean that the magnetosheath plasma, instead
of diverging from the subsolar streamline, converges toward it,
which is impossible. This suggests that the flow is highly variable during
this period, and this is not surprising. Indeed, judging on the plasma
velocity near the bow shock ( v
Values of the magnetosheath parameters obtained for this
crossing
were analyzed in the same manner as above.
The bottom curve in Figures 10a and 10b shows
the variation of the plasma compression index
C(x). One can see from
Figure 10a
that contrary to the previous case, the value of
C(x) at the
beginning of the profile is positive. For
a stationary flow this would mean that the magnetosheath plasma, instead
of diverging from the subsolar streamline, converges toward it,
which is impossible. This suggests that the flow is highly variable during
this period, and this is not surprising. Indeed, judging on the plasma
velocity near the bow shock ( v 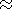 250 km s
-1 ),
the solar wind velocity
at that time has a value of about
1000 km s
-1, which corresponds
to a sporadic high-velocity stream which as a rule is greatly irregular.
Thus we may expect some contradictory results for this part of the profile.
250 km s
-1 ),
the solar wind velocity
at that time has a value of about
1000 km s
-1, which corresponds
to a sporadic high-velocity stream which as a rule is greatly irregular.
Thus we may expect some contradictory results for this part of the profile.
At x>10,000 km, C(x) is negative, and its variation corresponds to the stationary flow in the remaining part of the magnetosheath with the exception in the close vicinity of the magnetopause, where C(x) rapidly decreases. The variation of C(x) may be explained by the fact that plasma streamlines in the vicinity of the magnetopause are tangential to the magnetopause, so the satellite is moving there not along a streamline but perpendicularly to the line.
The observed profile of
T along with profiles of
T
along with profiles of
T calculated for different values
of
t from
the observed profiles of
B(x),
n(x), and
v(x) are also shown in Figure 10a. From a comparison of the model curves
with the experimental one, one can see that the latter is close to the model
profile with
t =5 s.
calculated for different values
of
t from
the observed profiles of
B(x),
n(x), and
v(x) are also shown in Figure 10a. From a comparison of the model curves
with the experimental one, one can see that the latter is close to the model
profile with
t =5 s.
As for the longitudinal temperature
T (Figure 10b), the
experimental curve is initially below all the model curves, which means that
T
(Figure 10b), the
experimental curve is initially below all the model curves, which means that
T decreases at that time
more rapidly than adiabatically.
This may be explained either by the existence of
rather effective sinks of the parallel energy or, and this seems to be
more likely, by the nonstationarity of the flow during this time.
For
x>15,000 km (with exception of a close vicinity to the magnetopause),
the variation of
T
decreases at that time
more rapidly than adiabatically.
This may be explained either by the existence of
rather effective sinks of the parallel energy or, and this seems to be
more likely, by the nonstationarity of the flow during this time.
For
x>15,000 km (with exception of a close vicinity to the magnetopause),
the variation of
T corresponds, judging
on
the slope of the curves, to a flow with
t=50-100 s.
corresponds, judging
on
the slope of the curves, to a flow with
t=50-100 s.
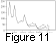 Results of calculation of
t
Results of calculation of
t and
t
and
t from the
B(x), n(x),
T
from the
B(x), n(x),
T (x), and
T
(x), and
T (x) profiles using
the formulae
(18) and (19) are presented in Figure 11. The value of
t
(x) profiles using
the formulae
(18) and (19) are presented in Figure 11. The value of
t for
x<15,000 km could not be obtained for the reasons
mentioned above. At
x>15,000 km, where the plasma flow
seems to be relatively
stationary, one can see that
t
for
x<15,000 km could not be obtained for the reasons
mentioned above. At
x>15,000 km, where the plasma flow
seems to be relatively
stationary, one can see that
t and
t
and
t are rather close to each other and equal to 10-50 s,
which is by 0.5-1 order
of magnitude less than in the previous case. This may be explained by
different values of the magnetosheath parameters and plasma velocity
during the two crossings.
are rather close to each other and equal to 10-50 s,
which is by 0.5-1 order
of magnitude less than in the previous case. This may be explained by
different values of the magnetosheath parameters and plasma velocity
during the two crossings.
The mirror-wave instability criterion Kph is also shown in Figures 10a and 10b, and as in the previous case, the rapid increase of the pitch-angle diffusion observed at x=10,000-15,000 km seems to be associated with the increase of the rate of the plasma expansion along the magnetic field rather than with any variation of the Kph value.
 Variations of the adiabatic indices are presented in Figure 12.
As one can see from Figure 12, variations of
g
Variations of the adiabatic indices are presented in Figure 12.
As one can see from Figure 12, variations of
g ,
g
,
g ,
and
Sg
indices along the first (outer) part of the
crossing significantly differ from the model ones, which seems to be
explainable in this case mainly by the nonstationary character of the flow
at that time. As in the previous case, the values of the three polytropic
indices within the inner layers of the magnetosheath are
close to those predicted by the adiabatic model.
,
and
Sg
indices along the first (outer) part of the
crossing significantly differ from the model ones, which seems to be
explainable in this case mainly by the nonstationary character of the flow
at that time. As in the previous case, the values of the three polytropic
indices within the inner layers of the magnetosheath are
close to those predicted by the adiabatic model.
The profile of
geff is seen to agree, on the whole,
with the model;
 geff
geff = 1.6 for the entire profile under consideration,
which is
close to the
= 1.6 for the entire profile under consideration,
which is
close to the
 geff
geff value obtained for the previous
case.
value obtained for the previous
case.
Thus in spite
of the difference in the flow characteristics during corresponding periods
the analysis of the experimental variations of the plasma and magnetic
field parameters during the two magnetosheath crossings
shows that one can distinguish two regions in the magnetosheath: an outer
one, from the bow shock to approximately the point where the plasma density
approaches its maximum, and an inner one, leading up to the magnetopause.
In the first region the energy transfer between the perpendicular and
the parallel temperatures is relatively slow, which taking into account the
observational noise makes it difficult to obtain there values
of the adiabatic indices and of the characteristic relaxation time
t.
Nevertheless, the results obtained allow us to suppose that the
T variations in this region
proceed almost adiabatically.
At the same time, the perpendicular temperature
T
variations in this region
proceed almost adiabatically.
At the same time, the perpendicular temperature
T increases in
this region significantly slower
than is predicted by the double-adiabatic law, which suggests the existence
of some dissipative process
[Hau, 1996;
Hau et al., 1993].
increases in
this region significantly slower
than is predicted by the double-adiabatic law, which suggests the existence
of some dissipative process
[Hau, 1996;
Hau et al., 1993].
In the second region the estimates of
t,
obtained from
T and
T
and
T ,
are close to each other, which suggests an effective energy
transfer between the perpendicular and the parallel temperatures.
The model of the
plasma turbulence responsible for the proton pitch-angle diffusion is not
quite clear. However, on the basis of the fact that the mirror-wave
instability criterion is not fulfilled in the second part of the profile on
October 24, 1985, this turbulence may be
associated with the development of the ion-cyclotron instability
[Gary, 1992].
,
are close to each other, which suggests an effective energy
transfer between the perpendicular and the parallel temperatures.
The model of the
plasma turbulence responsible for the proton pitch-angle diffusion is not
quite clear. However, on the basis of the fact that the mirror-wave
instability criterion is not fulfilled in the second part of the profile on
October 24, 1985, this turbulence may be
associated with the development of the ion-cyclotron instability
[Gary, 1992].
Results of the analysis presented above may be summarized as follows:
1. Variations of the perpendicular ( T ) and parallel ( T
) and parallel ( T )
temperatures along the subsolar streamline in the magnetosheath are calculated
for a model adiabatic flow. The profiles of
T
)
temperatures along the subsolar streamline in the magnetosheath are calculated
for a model adiabatic flow. The profiles of
T (x) and
T
(x) and
T (x) obtained are
used to estimate variations
of the adiabatic indices
g
(x) obtained are
used to estimate variations
of the adiabatic indices
g and
g
and
g across the magnetosheath. It is shown
that both indices significantly change along the streamline.
across the magnetosheath. It is shown
that both indices significantly change along the streamline.
2. The analysis of the experimental profiles of
T and
T
and
T shows that they
essentially differ from the adiabatic ones, which suggests the existence of
some nonideal processes which may be associated with the pitch-angle
diffusion of protons.
shows that they
essentially differ from the adiabatic ones, which suggests the existence of
some nonideal processes which may be associated with the pitch-angle
diffusion of protons.
3. As the numerical model simulation shows, the energy transfer between the
perpendicular and the parallel proton temperatures significantly changes not only
the temperature ( T , T
, T ,
and
T ) profiles but also the values
of the polytropic indices
g
,
and
T ) profiles but also the values
of the polytropic indices
g ,
g
,
g ,
and
geff.
Thus the observed deviation of those indices from their adiabatic values does
not necessarily mean that the process under consideration is not adiabatic
(see the discussion by
Denton et al. [1994],
Hau [1996], and
Hau et al. [1993]),
and some additional analysis of experimental data is needed.
,
and
geff.
Thus the observed deviation of those indices from their adiabatic values does
not necessarily mean that the process under consideration is not adiabatic
(see the discussion by
Denton et al. [1994],
Hau [1996], and
Hau et al. [1993]),
and some additional analysis of experimental data is needed.
4. The relaxation time of the proton temperature
anisotropy obtained from experimental
T profiles
( t
profiles
( t )
within the outer magnetosheath is
systematically greater than the time obtained from
the
T
)
within the outer magnetosheath is
systematically greater than the time obtained from
the
T variations
( t
variations
( t ).
This means that the rate of the perpendicular energy decrease
is greater than the rate of the parallel
energy increase, which suggests the existence of perpendicular energy sinks,
the nature of those sinks being yet unclear.
).
This means that the rate of the perpendicular energy decrease
is greater than the rate of the parallel
energy increase, which suggests the existence of perpendicular energy sinks,
the nature of those sinks being yet unclear.
5. In spite of a rather complicated behavior of
g and
g
and
g indices, the effective polytropic index
geff calculated for the entire magnetosheath
is equal to 1.7 for the crossing presented
by
Hill et al. [1995], and
indices, the effective polytropic index
geff calculated for the entire magnetosheath
is equal to 1.7 for the crossing presented
by
Hill et al. [1995], and
 geff
geff
 = 1.6 for the
crossing discussed by
Hau et al. [1993].
This may explain why the
estimates of the polytropic index obtained from the characteristics of the
magnetosheath as a whole
[Fairfield, 1971;
Farris et al., 1991;
Peredo et al., 1995;
Zhuang and Russell, 1981]
give a value of
g approximately equal to
5/3.
= 1.6 for the
crossing discussed by
Hau et al. [1993].
This may explain why the
estimates of the polytropic index obtained from the characteristics of the
magnetosheath as a whole
[Fairfield, 1971;
Farris et al., 1991;
Peredo et al., 1995;
Zhuang and Russell, 1981]
give a value of
g approximately equal to
5/3.
Belmont, G., and C. Mazelle, Polytropic indices in collisionless plasmas: Theory and experiment, J. Geophys. Res., 97, 8327, 1992.
Chew, G. F., M. L. Goldberger, and F. E. Low, The Boltzmann equation and the one fluid hydromagnetic equations in the absence of particle collisions, Proc. R. Soc. London, Ser. A, 236, 112, 1956.
Denton, R. E., B. J. Andersson, S. P. Gary, and S. A. Fuselier, Bounded anisotropy fluid model for ion temperatures, J. Geophys. Res., 99, 11,225, 1994.
Fairfield, D. M., Average and unusual location of the Earth's magnetopause and bow shock, J. Geophys. Res., 76, 6700, 1971.
Farris, M. H., S. M. Petrinec, and C. T. Russell, The thickness of the magnetosheath: Constraints on the polytropic index, Geophys. Res. Lett., 18 (10), 1821, 1991.
Feldman, W. C., Magnetic reconnection in the terrestrial magnetosphere, in Magnetospheric Phenomena, pp. 145-156, Astrophys. Workshop, New York, 1986.
Gary, S. P., The mirror and ion cyclotron anisotropy instabilities, J. Geophys. Res., 97, 8519, 1992.
Hau, L.-N., Nonideal MHD effects in the magnetosheath, J. Geophys. Res., 101, 2655, 1996.
Hau, L.-N., T.-D. Phan, B. U. Ö. Sonnerup, and G. Paschmann, Double-polytropic closure in the magnetosheath, Geophys. Res. Lett., 20 (20), 2255, 1993.
Hesse, M., and J. Birn, MHD modeling of magnetotail instability for anisotropic pressure, J. Geophys. Res., 97, 10,643, 1992.
Hill, P., G. Paschmann, R. G. Treumann, W. Baumjohann, N. Sckopke, and H. Lühr, Plasma and magnetic field behavior across the magnetosheath near local noon, J. Geophys. Res., 100, 9575, 1995.
Peredo, M., J. A. Slavin, E. Mazur, and S. A. Curtis, Three-dimensional position and shape of the bow shock and their variation with Alfvénic, sonic and magnetosonic Mach numbers, and interplanetary magnetic field orientation, J. Geophys. Res., 100, 7907, 1995.
Phan, T.-D., G. Paschmann, W. Baumjohann, N. Sckopke, and H. Lühr, The magnetosheath region adjacent to the dayside magnetopause: AMPTE/IRM observations, J. Geophys. Res., 99, 121, 1994.
Pudovkin, M. I., and V. V. Lebedeva, Solar wind parameters in the magnetosheath in a model with a magnetic barrier, Geomagn. Aeron. (in Russian), 27 (1), 22, 1987.
Pudovkin, M. I., and S. V. Smolin, Pitch-angle particle distribution in the convecting magnetospheric plasma, Geomagn. Aeron. (in Russian), 28 (2), 268, 1988.
Pudovkin, M. I., B. P. Besser, V. V. Lebedeva, S. A. Zaitseva, and C.-V. Meister, Magnetosheath model in the Chew- Goldberger-Low approximation, Physics of Plasma, 6 (7), 2887, 1999.
Pudovkin, M. I., C.-V. Meister, B. P. Besser, and H. K. Biernat, The effective polytropic index in a magnetized plasma, J. Geophys. Res., 102, 27,145, 1997.
Pudovkin, M. I., V. S. Semenov, H. K. Biernat, G. A. Bachmaier, and M. T. Kiendl, Structure of the subsolar magnetopause on November 1, 1978, 1510-1530 UT: An effect of reconnection?, J. Geophys. Res., 100, 19,239, 1995a.
Pudovkin, M. I., S. A. Zaitseva, and B. P. Besser, Magnetopause magnetic barrier parameters in dependence on the solar wind magnetic field orientation, Ann. Geophys., 13, 828, 1995b.
Shishkina, E. M., M. I. Pudovkin, and N. G. Matveeva, Peculiarities of pitch-angle diffusion in auroral plasma at initial and active phases of substorms, Proc. Arc. Antarct. Res. Inst. (in Russian), 436, 35, 1995.
Slavin, J. A., D. S. Chaussee, R. E. Holzer, J. H. Spreiter, and S. S. Stahara, Solar wind flow about the terrestrial planets, 2, Comparison with gas dynamic theory and implications for solar-planetary interactions, J. Geophys. Res., 88, 19, 1983.
Zhuang, H. C., and C. T. Russell, An analytic treatment of the structure of the bow shock and magnetosheath, J. Geophys. Res., 86, 2191, 1981.