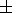 90 V, this value being
limited by the amplifier. The detector part of the device was fixed
at the rod and installed at a distance of 1 m in front of the solar
panels in the direction of the spacecraft velocity.
90 V, this value being
limited by the amplifier. The detector part of the device was fixed
at the rod and installed at a distance of 1 m in front of the solar
panels in the direction of the spacecraft velocity.
V. N. Oraevsky, V. S. Dokukin, A. S. Volokitin, S. A. Pulinets, and Yu. Ya. Ruzhin
Institute of Terrestrial Magnetism, Ionosphere, and Radio Wave Propagation, Troitsk, Moscow Region, Russia
E. Chouieri
Electric Propulsion and Plasma Dynamics Laboratory, Princeton University, New Jersey, Princeton, USA
V. V. Afonin
Institute of Space Research, Moscow, Russia
The phenomenon of critical ionization velocity (CIV) is a fast (abnormal) ionization of a neutral gas occurring when the relative speed of a gas cloud in a magnetized plasma exceeds some critical value at which the atom kinetic energy is higher than its ionization potential. This fundamental phenomenon of plasma physics was proposed by Alfvén [1954] as an explanation of various aspects of the formation of the solar system and ionospheres of both distant planets and comets. The CIV phenomenon includes, as an essential component, the development of low-frequency plasma turbulence due to interaction of the ion beam with the plasma waves. The wave-particle and nonlinear wave-wave interactions, characteristic for this low-frequency turbulence, provide heating and acceleration of electrons and, as result, ionization of the neutral gas [Haerendel, 1982; Papadopoulos, 1985].
The CIV phenomenon was a goal of many theoretical [Galeev and Chabibrachmanov, 1986] and experimental [Torbert, 1990] investigations over the last few years. An opportunity to use the Earth's ionosphere and magnetosphere as an ideal laboratory for the experimental study of the CIV phenomenon is attractive, and a number of active experiments in space with injection of neutral gas has been carried out: Porcupine [Torbert, 1990], Condor [Haerendel et al., 1986], Star of Lima [Wescott et al., 1986], the ATLAS 1 [Marshall et al., 1993]. The observations of a low-frequency turbulence excited in a magnetized plasma by an ion beam or plasma jet, obtained in the COMBI and Porcupine rocket experiments, are of interest also for studying the CIV phenomenon, as a basic process, controlling ionization of a neutral gas cloud. Unfortunately, many CIV details in these experiments still remain obscure and even a manifestation of the CIV in some of them remains doubtful.
Conducting the experiments with injection of xenon plasma (beams of Xe ions) in the ionosphere in the scope of the APEX (Active Plasma Experiment, which was an Institute of Terrestrial Magnetism, Ionosphere, and Radio Wave Propagation (IZMIRAN) project) program, there were more than 20 cases not planned beforehand, when the plasma gun operated in a mode of neutral gas injection. Under the conditions of the APEX the kinetic energy of the relative movement of Xe atoms and the ionospheric plasma exceeded the xenon ionization potential, so the obligatory condition of the CIV phenomenon was fulfilled. The injections of neutral xenon were made in a height range from 400 up to 3000 km. The experimental conditions (the values of the geomagnetic field, background density, angle between the vector of the gas velocity and the magnetic field, etc.) considerably changed along the polar orbit of the spacecraft, and this is a distinctive feature of the experiment as compared with other experiments, for example, ATLAS 1.
Since the research of anomalous ionization was not part of the original APEX program, the satellite was not designed with an ability to increase the neutral xenon mass flow above the nominal value of 3 mg s -1. This is 3 orders of magnitude lower than the gas output in the ATLAS 1 experiment. However, contrary to the gas injections at ATLAS 1, which lasted 100 ms each, the duration of the gas releases in APEX was a few minutes.
Analyzing the APEX data for the processes responsible for CIV, one should investigate the following: influence of the gas injection on the electron distribution and the spectra of low-frequency plasma waves, dependence of the plasma turbulence spectra on the angle between the magnetic field and the gas motion direction, and other effects. The observations of the xenon ions with the characteristic energy corresponding to the kinetic energy of the atoms, the spectra of accelerated electrons, and electric field oscillations in the vicinity of the lower hybrid resonance also are of interest.
The data obtained in the experiment indicate that the ambient plasma reacted to the impact of the neutral gas flow. In some cases, changes in the density, temperature and plasma anisotropy, variations of the spacecraft potential, and an increase of the wave activity almost in the entire frequency range are observed.
The structure of the paper is as follows: Section 2 describes briefly the satellite instrumentation. Section 3 discusses the experimental data based mainly on the onboard observations of the cold plasma and HF waves. A theoretical analysis of the interaction of the neutral cloud with the plasma in the APEX is presented in section 4. The analysis includes consideration of the processes of the gas preionization and formation of a nonequilibrium distribution of the ions, quasi-linear theory of instability of a spatially limited ion beam in the plasma, including electron heating in this process, and also discussion of extra ionization of the neutral gas and other effects accompanying CIV. Section 5 contains the results of the above analysis.
The scientific equipment onboard the Intercosmos 25 spacecraft includes two electron guns with the acceleration voltage of 8 keV and a current of 100 mA, the injector of neutral gas and Xe plasma with the effective current of 2-4 A, and also the scientific devices, which provide measurements of microparameters and macroparameters of the thermal and "suprathermal" plasma components, quasi-constant components of the magnetic and electric fields, and electromagnetic fields in the ELF/VLF/LF/HF ranges. The devices, whose measurements are of interest in studying anomalous ionization, are briefly described below.
The HF wave block provided measurements of one component of the electric and magnetic field in the frequency range 0.1-10 MHz. The data are discussed below.
The ionospheric plasma parameters (the ion density and three
components of the electron temperature) were measured by the KM-10
device, which uses
flat nickel probes with a diameter of
3.5 cm
as sensors.
One of the probes was chosen for permanent control of the
probe potential relative to the spacecraft body. Due to a high
input impedance of the differential amplifier, the probe potential
was close to the one given by the balance between the electron flux
and the flux of the inflowing ions. The KM-10 device was able to
measure the potential residual up to
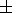 90 V, this value being
limited by the amplifier. The detector part of the device was fixed
at the rod and installed at a distance of 1 m in front of the solar
panels in the direction of the spacecraft velocity.
90 V, this value being
limited by the amplifier. The detector part of the device was fixed
at the rod and installed at a distance of 1 m in front of the solar
panels in the direction of the spacecraft velocity.
The quasi-constant magnetic field was measured by the three-axis
magnetometer with a dynamical regime of
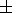 64,000 nT. The data of
the other (service) three-axis magnetometer, which was a part of
the navigation system, were also available.
64,000 nT. The data of
the other (service) three-axis magnetometer, which was a part of
the navigation system, were also available.
Xenon injection was conducted through a stationary plasma injector (UPM), which operated in the regime without discharge ignition. The plasma injector was put into the upper part of the spacecraft with its axis directed under an angle of 45o to the spacecraft vertical axis. Due to some technical reasons, the ionization voltage was not switched on in 20 operational series. The standard regimes of the UPM operation contained a 5 to 6 s interval with a release of xenon neutral atoms in the beginning of each session. The kinetic energy of the xenon atom relative motion was above 20 eV and exceeded significantly the xenon ionization potential UI = 12.13 eV; however, the total mass of the injected xenon atoms was relatively small, and so one should hardly expect observation of all the manifestations of the anomalous ionization process (a total CIV) in these experiments. Nevertheless, some physical processes participating in CIV may be observed.
The only distinct manifestation of effects of the neutral gas injection in the observational data analyzed up to date is in the results of the wideband measurements of HF waves in the MHz range. Most probably, this result of the search for manifestation of the anomalous ionization processes may be due to the low flux density (small mass) of the gas injected in the APEX experiment. Even if the conditions of ion beam instability were realized, the turbulence developed was much weaker than that registered in the ATLAS 1 experiment [Marshall et al., 1993].
The HF wave activity observations are represented by the following broadband data, which demonstrate two cases of injection with high and low pitch angles and manifest distinctly strong pitch-angle dependence. The observed effects may be summarized as follows:
In all neutral xenon releases studied with a high (close to the normal) pitch angle (between 85o and 115o) an intensification of the emission of the HF plasma waves in the frequency range 3-10 MHz is observed.
In all releases with low pitch angle (between 57o and 71o) studied, no such intensification of the wave emission was observed.
 Figure 1 shows typical broadband HF spectra in the range
1-10 MHz for the neutral xenon injection at orbit 419 (the orbit
parameters are shown in Table 1). The signal amplitude is shown by
the color, the injection moments are shown by
vertical lines. The red curves show the first three harmonics of the
electron cyclotron frequency. The injection was conducted with a
high pitch angle, beginning from
94.8o at valve opening
moment and ending at
113o at closing.
Figure 1 shows typical broadband HF spectra in the range
1-10 MHz for the neutral xenon injection at orbit 419 (the orbit
parameters are shown in Table 1). The signal amplitude is shown by
the color, the injection moments are shown by
vertical lines. The red curves show the first three harmonics of the
electron cyclotron frequency. The injection was conducted with a
high pitch angle, beginning from
94.8o at valve opening
moment and ending at
113o at closing.
Figure 1 shows the following features of the broadband spectra:
1. There is wave activity in a narrow band (manifested as a light blue band with some green in it) with a center at approximately 3.7 MHz, which begins at the valve switching on (with the accuracy up to the device resolution) and continues till the valve is switched off.
2. There is more wideband activity, mainly manifested as a green band with some blue colors spread from 8 MHz up to a frequency of at least 10 MHz. This wave activity has the same properties as the above described narrowband activity, except that the emission stops more abruptly when the valve is switched off.
3. Both of the above described wave bands are horizontal and do not manifest temporal changes in the magnetic field, which would cause variations in the electron-cyclotron frequency harmonics shown in Figure 1.
4. All other properties are either natural ionospheric phenomena or wave activity, which is not influenced by the neutral gas release.
Complete explanation of the character of this wave activity is a hard task. Since the frequencies of the amplified waves do not manifest significant changes in the magnetic field and density during the data registration time, they cannot be directly related to the natural plasma frequencies. Nevertheless, the fact stays that their appearance and properties observed correspond well to the gas release events.
 Another example of the broadband HF data for a release with
high
pitch angle is shown in Figure 2. The injection took place at orbit
490 with the parameters shown in Table 1. The same comments are
true here as have been done for Figure 1 (for orbit 419) with some
addition that there is a distinct increase of the broadband noise
over the entire spectrum. The increase starts from the moment of
the switching on the cathode heater and stops at the moment of
switching off all UPM subsystems.
Another example of the broadband HF data for a release with
high
pitch angle is shown in Figure 2. The injection took place at orbit
490 with the parameters shown in Table 1. The same comments are
true here as have been done for Figure 1 (for orbit 419) with some
addition that there is a distinct increase of the broadband noise
over the entire spectrum. The increase starts from the moment of
the switching on the cathode heater and stops at the moment of
switching off all UPM subsystems.
 An example of the injection with low pitch angle is shown
in Figure 3
for orbit 496. The corresponding orbital data are also shown in
Table 1.
An example of the injection with low pitch angle is shown
in Figure 3
for orbit 496. The corresponding orbital data are also shown in
Table 1.
Contrary to the high-angle injection discussed above, these data show no change in the wave activity, which might have been related to any event of the neutral gas release.
 The results of the measurements of the cold plasma parameters in
the periods of neutral gas injection show no significant changes in
the plasma density. Figure 4 shows the results of the measurements
of the plasma density and temperature and the spacecraft potential
by the KM-10 device at orbit 419.
These data
have been filtered to exclude telemetry noise
and demonstrate rather strong variations of
the plasma density and temperature and also of the spacecraft
potential not related to the xenon injection.
The results of the measurements of the cold plasma parameters in
the periods of neutral gas injection show no significant changes in
the plasma density. Figure 4 shows the results of the measurements
of the plasma density and temperature and the spacecraft potential
by the KM-10 device at orbit 419.
These data
have been filtered to exclude telemetry noise
and demonstrate rather strong variations of
the plasma density and temperature and also of the spacecraft
potential not related to the xenon injection.
 The variations of the plasma density and electron temperature
along
and across the magnetic field are shown in Figure 5 versus the
number of the telemetry frame, which corresponds to a time
dependence. In spite of the fact that a strong noise related to
telemetry fails is seen in Figure 5, the character of
the
r and
Te changes
is fairly distinct, and one can conclude that there is no
significant changes in the density related to the gas injection.
There is a small peak at the temperature dependence, which
coincides with the time of gas injection, but it is, most probably,
an effect of the heating or acceleration of the electrons under the
interaction of the xenon jet with the ambient plasma.
The variations of the plasma density and electron temperature
along
and across the magnetic field are shown in Figure 5 versus the
number of the telemetry frame, which corresponds to a time
dependence. In spite of the fact that a strong noise related to
telemetry fails is seen in Figure 5, the character of
the
r and
Te changes
is fairly distinct, and one can conclude that there is no
significant changes in the density related to the gas injection.
There is a small peak at the temperature dependence, which
coincides with the time of gas injection, but it is, most probably,
an effect of the heating or acceleration of the electrons under the
interaction of the xenon jet with the ambient plasma.
It should be emphasized that though the above described effects correlate well with the pitch angle in all the cases considered, it is still obscure, whether this correlation is of a random character or whether the appearance of the above mentioned emissions is governed by other conditions, for example, by the position at the orbit and plasma parameters which correlate with the pitch angle.
In particular, it is interesting that all the high pitch-angle injections studied were carried out under solar illumination, whereas all the small pitch-angle injections were conducted in darkness. This fact is a consequence of the unplanned synchronism between the motion along the polar orbit, solar illumination cycle and injection program. Therefore it is possible that the presence of the sunlight fluxes, but not the pitch angle value, is the governing parameter for the effects described above. In this case the role of the solar flux, in excitation of the broadband HF activity by the effects of the type of plasma expansion due to the photoionization, is worth studying. Since the changes in the sunlight flux during the injection time are small and the gas expenditure under the injection is constant, such a mechanism may provide explanation to the constancy of the excited band frequency with time.
In conclusion, we cannot exclude the role of ground-based radio sources in formation of the horizontal frequency bands observed in the spectra. However, the question still remains, why these bands appear (or are intensified) only during injections.
The gas expenditure in the regime of neutral gas injection
corresponds to the injection plasma current (2-3 A) of
dNXe/dt = 2-6  1019
atoms per second. The mean release velocity
v is
1-2 vT ( vT being the Xe thermal velocity in the reservoir).
Though the value of
vT is not exactly known, one can accept that
vT
1019
atoms per second. The mean release velocity
v is
1-2 vT ( vT being the Xe thermal velocity in the reservoir).
Though the value of
vT is not exactly known, one can accept that
vT 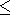 104 cm s
-1.
As a result, a neutral gas cloud, which moves
with a velocity of
5
104 cm s
-1.
As a result, a neutral gas cloud, which moves
with a velocity of
5  8 km s
-1 through the ambient plasma, is
formed around the spacecraft. We assume that the cloud forms a
spherical cone with the angle of
60o and a ring in the lateral
cross section. Assuming that the gas density in the spherical cone
is homogeneous within the cross section (to be more exact, one can
assume a Gaussian distribution of the density), one can express it
at a distance
r as
8 km s
-1 through the ambient plasma, is
formed around the spacecraft. We assume that the cloud forms a
spherical cone with the angle of
60o and a ring in the lateral
cross section. Assuming that the gas density in the spherical cone
is homogeneous within the cross section (to be more exact, one can
assume a Gaussian distribution of the density), one can express it
at a distance
r as
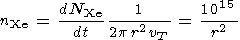 | (1) |
Here
d NXe / dt = (2-6) 1019
atoms per second and the velocity
v = vT
1019
atoms per second and the velocity
v = vT 104 cm s
-1.
For example, at
r = 100 m and 1000 m,
nXe = 109 cm
-3 and
107 cm
-3, respectively.
104 cm s
-1.
For example, at
r = 100 m and 1000 m,
nXe = 109 cm
-3 and
107 cm
-3, respectively.
If some of these Xe atoms are ionized, the interaction of these ions with the ambient plasma may initiate a process of anomalous ionization. There are several possibilities to reach the necessary preionization. They are as follows: ionization by electric charges in the injector, Xe atom ionization in inelastic collisions with the ions of the ambient plasma with charge transfer, electron impact ionization in collisions with the plasma electrons, and photoionization. We assume that at least in 20 cases of neutral gas release, the first possibility should be excluded. So we consider the efficiency of the latter three processes.
Inelastic collisions of the Xe atoms with O
+ ions with a charge
transfer have the cross section
sch  2
2  10-15 cm
2, which is lower than the elastic collision
cross section. The
local formation rate of the Xe ions in the charge transfer reaction
may be evaluated as
10-15 cm
2, which is lower than the elastic collision
cross section. The
local formation rate of the Xe ions in the charge transfer reaction
may be evaluated as
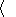 sch niv
sch niv
 nXe
nXe
Bearing in mind that the number of the atoms injected increases linearly with time, we obtain, after integration over the volume, the total number of the Xe ions formed during time t in charge transfer collisions with plasma ions
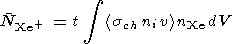 |
 |
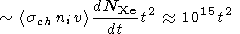 |
One can hardly expect an ability to observe the newly born ions by
the diagnostics available at the spacecraft. First of all, the
Larmor radius of the Xe ions is high ( rL 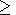 500 m). Then,
the Xe
ions never reach the spacecraft (the diagnostic tools) because of
both, [
E
500 m). Then,
the Xe
ions never reach the spacecraft (the diagnostic tools) because of
both, [
E B ] drift and the initial velocities.
B ] drift and the initial velocities.
The evaluation of the number of the Xe ions formed in inelastic collisions with the plasma electrons may be done in the same way as it has been done in the previous section. However, a significant difference should be taken into account. Under the ambient plasma electron temperature of 1-2 eV, the number of the electrons with the energy exceeding the ionization potential is very low. Therefore the effective ionization frequency
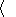 se
ionne v
se
ionne v 
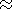 10-16 ne
vTe e-eUi/Te
10-16 ne
vTe e-eUi/Te
and the local ion formation rate may be evaluated by
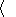 se ionne
v
se ionne
v  nXe
nXe 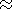 10-16 ne vTe
e-eUi/Te nXe
10-16 ne vTe
e-eUi/Te nXe
Now we obtain the evaluation of the total Xe ion formation under the electron impact ionization
 |
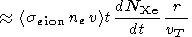 |
 | (2) |
and see that the ionization rate in the charge transfer reaction is higher by 2 orders of magnitude.
The consequences of the Xe ion appearance in the environment under neutral gas injection are discussed below. However, there is another process, not considered above, which is a more effective source of plasma disturbance, leads to a heating of the ambient plasma, and creates prerequisites to anomalous ionization. The process is the reflection of the ambient plasma ions under elastic collisions with the neutral gas jet, which we consider in section 4.3.
The gas density in the vicinity of the injector is high, and collisions of the Xe atoms with the ambient ions may be significant. We evaluate the distance from the injector at which the mean free path of the ions in the neutral gas l = 1/snXe is less than or equal to this distance ( rc = l ). If the elastic collision cross section s is 10-14 cm 2, at the distance of less than 10-20 cm from the injector, actually the entire flux of the ionospheric plasma through the very beginning of the Xe cloud would be stopped (or reflected and scattered) due to collisions with the neutrals.
The inelastic collisions are able to influence
the distribution function up to a distance of
100-300 cm. The probability of an ionospheric ion to be scattered
in the Xe cloud at the path
dl is about
dl/l.
Then passing
the path
dl through the cross section
dS in the Xe cloud,
the ionospheric ion flux of about
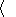 niv
niv  loses
loses
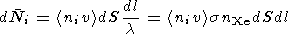 |
particles per second. The total number of the ionospheric ions reflected per second is given by
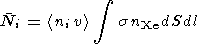 |
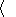 ni v
ni v  snXe
dV =
snXe
dV = 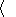 ni v
ni v
 sNXe
sNXe
where
NXe is the total number of the injected Xe atoms. Thus
under typical parameters ( ni 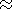 104,
v
104,
v 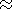 vsc
vsc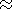 8
8  106 cm s
-1 )
after
t seconds the total flux of the scattered
O
+ ions is
106 cm s
-1 )
after
t seconds the total flux of the scattered
O
+ ions is
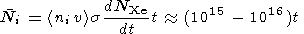 | (3) |
The oxygen ion energy almost do not change after a collision
because of the large difference between the O
+ and the Xe masses. So
as a first approximation, the reflected ion distribution may be
considered as isotropic in the frame of reference of the Xe cloud
(spacecraft). The ionospheric ions reflected from the neutral cloud
are magnetized and continue the [
E B ]
drift in the cloud system
together with the main flux. However, in the frame of reference of
the ionospheric plasma at a distance shorter than the Larmor
radius, the reflected ions or a hot ion flux with the drift
velocities about
vsc and the velocity scatter within about
(1/2-1/3)vsc.
B ]
drift in the cloud system
together with the main flux. However, in the frame of reference of
the ionospheric plasma at a distance shorter than the Larmor
radius, the reflected ions or a hot ion flux with the drift
velocities about
vsc and the velocity scatter within about
(1/2-1/3)vsc.
Thus some part of the ionospheric ion flux is captured by the
neutral Xe cloud. This effect of raking together may be observed
and the ionospheric plasma ion density may increase. However, the main
effect of the ion collisions with the Xe gas is formation of an
unstable (beam)
velocity
distribution
and, as a result,
generation of the lower hybrid oscillations in the plasma. The ion
flux formed is significantly irregular in space. We are able to
evaluate the flux density, which is a principal parameter
controlling the instability conditions, if we assume that the
distance
R (the main input to the flux density) is provided by the
ions scattered for
r < R and
t 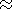 R/vT.
Thus
R/vT.
Thus
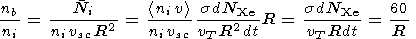 |
For
R 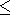 104 cm we obtain
nbni
104 cm we obtain
nbni 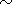 10-3-10-4.
10-3-10-4.
Acceleration or heating of the electrons by waves under development
of the ion-ion instability is usually considered as a significant
part in the chain of events leading to anomalous ionization in
the rarefied medium. Evaluation of the typical mean free path of
the ionospheric electrons in the Xe cloud under elastic collisions
( se- Xe 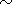 (0.3-1)
(0.3-1)  10-15 cm
2 )
and neutral density
r is given by
10-15 cm
2 )
and neutral density
r is given by
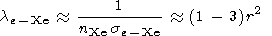 |
Here
r is the distance from the injector in meters. This formula
shows that the
e -Xe elastic collisions are significant up to
r 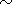 1 m. At distances
r > 3 m,
electron collisions occur very seldom to
change their dynamics or distribution. According to the previous
consideration, the density of the plasma ions scattered by the Xe
atoms is rather high at
r
1 m. At distances
r > 3 m,
electron collisions occur very seldom to
change their dynamics or distribution. According to the previous
consideration, the density of the plasma ions scattered by the Xe
atoms is rather high at
r 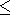 3 m, and in this region, oscillations
of the ion sound type may develop, leading to a strong heating of the
electrons (this is possible under their capture and crossing of
trajectories in the wave potential). The energy of the accelerated
electrons may be evaluated, if we assume that the ion-ion
instability is stabilized by the ion trapping in the potential hole
jtrapp. In this case the electron obtains
additional
energy
e
3 m, and in this region, oscillations
of the ion sound type may develop, leading to a strong heating of the
electrons (this is possible under their capture and crossing of
trajectories in the wave potential). The energy of the accelerated
electrons may be evaluated, if we assume that the ion-ion
instability is stabilized by the ion trapping in the potential hole
jtrapp. In this case the electron obtains
additional
energy
e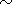 ejtrapp = mivdv
= 3
ejtrapp = mivdv
= 3 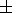 5 eV,
where
dv is the velocity shift between the beam and the wave. Thus the
heating of the electron to energies higher than the ionization
potential is possible only in resonance interaction with waves
of much longer wavelength in a much larger volume.
5 eV,
where
dv is the velocity shift between the beam and the wave. Thus the
heating of the electron to energies higher than the ionization
potential is possible only in resonance interaction with waves
of much longer wavelength in a much larger volume.
Thus the reflected ions form a bump-of-tail distribution near the
injector. In this case, development of ion-ion instability is
possible, because the relative velocity
Vb of the ionospheric
plasma and the ions of the beam exceeds significantly the thermal
velocity of the background plasma ions. The ion-sound instability
is suppressed in the ionosphere under
Te 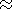 Ti,
and under
these conditions, the main instability is the instability of the
quasi-potential lower hybrid oscillations under their resonance
interaction with the ion beam
kVb
Ti,
and under
these conditions, the main instability is the instability of the
quasi-potential lower hybrid oscillations under their resonance
interaction with the ion beam
kVb 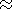 -k
-k | Vb |
| Vb |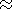 w = wc(kz/k),
where
wpe and
wc are
Langmuir and electron cyclotron frequencies, respectively. It is
assumed that
w
w = wc(kz/k),
where
wpe and
wc are
Langmuir and electron cyclotron frequencies, respectively. It is
assumed that
w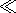 wc,
and the parallel vector of the
wave
kz is less than the
k
wc,
and the parallel vector of the
wave
kz is less than the
k vector perpendicular to the
magnetic field. Taking the wavelength of the instable wave to be
less than the ion cloud dimension, we calculate the local
instability increment of the ion beam according to
[Mikhailovskii, 1974]
vector perpendicular to the
magnetic field. Taking the wavelength of the instable wave to be
less than the ion cloud dimension, we calculate the local
instability increment of the ion beam according to
[Mikhailovskii, 1974]
 |
where DVb is the velocity dispersion in the beam, which in our case is about 1/2Vb.
The threshold of the ion-ion instability is determined by the
velocity, with which the wave exits the region of the interaction
with the beam. The velocity may be represented by the effective
attenuation rate
n = Vgz/R, where
Vgz is the group velocity
of the waves
Vgz = 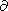 w
/
w
/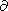 kz = w
/ kz.
The necessary condition
gb
kz = w
/ kz.
The necessary condition
gb 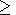 n is fulfilled if
kzR
n is fulfilled if
kzR 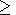 ninb
ninb
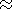 103.
103.
Above the threshold the instability is saturated because of the quasi-linear resonance interaction of electrons with the lower hybrid waves. If the equilibrium state is reached and there is a balance of the swinging and attenuation rates of the waves according to the equation
one is able to determine the distribution function of the electrons accelerated as a result of development of the ion beam instability. Here Wk is the wave energy density, ge is the Landau damping under the resonance w = kzvez with the magnetized electrons, which is given by the formula
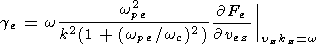 |
Using the equation
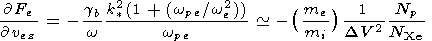 | (4) |
we find a solution [see Lizunov et al., 1995], which is a universal distribution of the accelerated electrons:
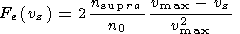 |
where
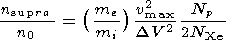 |
The maximum velocity, to which the waves may accelerate the electrons, is determined by the condition
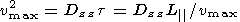 | (5) |
where
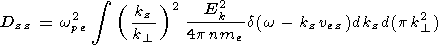 |
is the coefficient of the electron diffusion in the velocity space. Further we use the expression
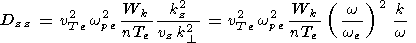 |
where
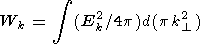 |
is the energy distribution along
the spectral lines, and the
k = k
= k (kz) ratio is taken
along this line. Taking into account the resonance condition
w/k
(kz) ratio is taken
along this line. Taking into account the resonance condition
w/k Vb,
we can estimate
Vb,
we can estimate
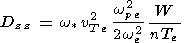 |
where
 |
and w* is the frequency, corresponding to maximum of the spectrum. Then from (4) and (5)
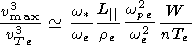 |
Unfortunately, the quasi-linear theory is not able to determine
W/nTe and
w* with reasonable accuracy. To be
able to accelerate
electron to energy exceeding the potential ionization
(vmax2 / vTe2  30),
one has to reach (at
wpe2/we2
= 10 and
w*
30),
one has to reach (at
wpe2/we2
= 10 and
w*  10-2we)
10-2we)
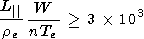 |
This condition is rather difficult but possible to satisfy at
realistic
W/Te = 3  10-2
and
L| = 105re.
10-2
and
L| = 105re.
The suprathermal electrons accelerated by the lower hybrid turbulence provide an extra source of ionization of Xe. The rate may be evaluated if one uses the calculated electron distribution in the same way as in section 4.2
 |
 |
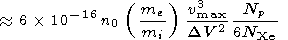 |
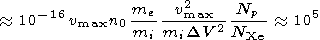 |
Here
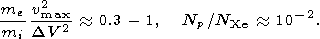 |
For example, only 1% of the atoms would be ionized during the neutral Xe injection time of about 1000 s.
 It follows from our theoretical consideration that
(1) the amount of the injected neutral Xe is small.
However, due
to the collisional interaction of this gas with the background
plasma, there appear enough initiating ions. They are new Xe ions
and the scattered ions of the ionospheric plasma.
(2) One may expect development of the ion-ion instability of
the lower hybrid waves at a distance of
r
It follows from our theoretical consideration that
(1) the amount of the injected neutral Xe is small.
However, due
to the collisional interaction of this gas with the background
plasma, there appear enough initiating ions. They are new Xe ions
and the scattered ions of the ionospheric plasma.
(2) One may expect development of the ion-ion instability of
the lower hybrid waves at a distance of
r  3-100 m. These
waves in the satellite frame of reference are perpendicular to
the magnetic field component of the phase velocity in the range of
the reflected ion velocities of 0-7 km s-1. Their group velocity is
directed mainly along the magnetic field, so they are able to reach
the spacecraft and be observed.
(3) In a quasi-linear interaction the lower hybrid wave
accelerates the electrons along the magnetic field up to
suprathermal energies. These electrons may reach the spacecraft and
be observed (see Figure 6).
(4) The expected flux of these electrons and the volume of
their collisional interaction with the neutral xenon is not enough
to produce a significant increase in the plasma density.
3-100 m. These
waves in the satellite frame of reference are perpendicular to
the magnetic field component of the phase velocity in the range of
the reflected ion velocities of 0-7 km s-1. Their group velocity is
directed mainly along the magnetic field, so they are able to reach
the spacecraft and be observed.
(3) In a quasi-linear interaction the lower hybrid wave
accelerates the electrons along the magnetic field up to
suprathermal energies. These electrons may reach the spacecraft and
be observed (see Figure 6).
(4) The expected flux of these electrons and the volume of
their collisional interaction with the neutral xenon is not enough
to produce a significant increase in the plasma density.
These conclusions agree with the observational data presented and make it possible to explain them. Unfortunately, the absence of the data on the low-frequency (lower hybrid) wave activity in the spectra of the energetic electrons makes it impossible to present a complete picture of the event and draw final conclusions.
Alfvén, H., On the Origin of the Solar System, Oxford Univ. Press, New York, 1954.
Galeev, A. A., and I. C. Chabibrachmanov, The critical ionization phenomenon in astrophysics, in Proceedings of the Joint Varenna-Abastumani International School and Workshop on Plasma Astrophysics, May 1986, ESA-SP-251, pp. 129-136, Eur. Space Agency, Paris, 1986.
Haerendel, G., Alfvén's critical velocity effect tested in space, Z. Naturforsch., 37a, 728, 1982.
Haerendel, G., M. C. Kelley, and R. F. Pfaff, Electric field measurements during the Condor critical velocity experiment, J. Geophys. Res., 91 (A9), 9939, 1986.
Lizunov, G. V., V. N. Oraevsky, and A. S. Volokitin, Whistler generation by an ion beam limited in the transverse direction, Plasma Phys. Rep., 21 (1), 85, 1995.
Marshall, J. A., J. L. Burch, E. Y. Chouieri, and N. Kawashima, CIV experiment on ATLAS 1, Geophys. Res. Lett., 20 (6), 499, 1993.
Mikhailovskii, A. B., Theory of Plasma Instabilities, Consult. Bur., New York, 1974.
Papadopoulos, K., On the physics of the critical ionization velocity phenomena, in Advances in Space Plasma Physics, pp. 33-58, Plasma Phys. Coll., Trieste, Italy, 1985.
Torbert, R. B., Review of critical velocity experiments in the ionosphere, Adv. Space Res., 10, 47, 1990.
Wescott, E. M., et al., Star of Condor: A strontium critical velocity experiment, Peru, 1983, J. Geopys. Res., 91, 9923, 1986.