V. A. Pilipenko and Yu. P. Kurchashov
Institute of Physics of the Earth, Moscow, Russia
Hydromagnetic diagnostics of the magnetospheric plasma density from ground-based data is based on signatures of the resonance effects in the spatial-spectral structure of the geomagnetic pulsation field. The gradient method [Baranskiy et al., 1985; Best et al., 1986] seems to be the most effective method for isolation of resonance frequencies in the spectrum of geomagnetic pulsations. This method is based on precision measurements of the H components of the pulsation field at two stations situated at a small spacing along the geomagnetic meridian. The physical basis of the gradient method is the characteristic feature of the spatial structure of the pulsation field in the resonance region, notably the superposition of the large-scale magneto-acoustic wave from the source and the local resonance response of the magnetospheric Alfvén resonator. It is the difference in spatial scales of these wave processes that provides the basic possibility of isolation of even feeble resonance effects. The gradient method has successfully been used for the determination of parameters of the magnetospheric resonator at middle and low latitudes from Pc3-4 pulsation data [Baranskiy et al., 1988; Fedorov et al., 1989; Pilipenko et al., 1988]. A modified gradient method ensures the determination of resonance magnetospheric frequencies even in the presence of lateral geoelectric inhomogeneity of the crust [Pilipenko and Fedorov, 1993]. To determine the resonance frequency of the field line running between the stations, the standard method uses either the ratio of the signal amplitude spectra [Baranskiy et al., 1985] or the difference of the phase spectra [Best et al., 1986; Waters et al., 1991].
In the present paper, we propose a geometric method for analyzing gradient measurement data, which simultaneously uses amplitude and phase information. To evaluate the new method, we used Pc4 pulsation data from a meridional network of magnetic stations in the L range from 4.7 to 3.0 [Green, 1978]. This event can be considered a reference event since it had received thorough study [Baranskiy et al., 1988; Fedorov et al., 1989] to demonstrate the resonance magnetospheric effects.
According to resonance theory (see the review by Pilipenko and Fedorov [1993] and references therein), the spectrum of the resonant component of a signal can be presented in the form
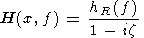 | (1) |
where z = (x-xR(f))/e is the normalized distance from the resonance point xR(f) ; hR(f) is the amplitude of pulsations at the resonance point, x is the field line coordinate measured along the geomagnetic meridian on the ground surface, and e is the half width of the resonance region. The x axis is directed from the source of oscillations. (It is assumed that the resonance frequency fR(x) increases with x and e >0 ). By measuring signal's resonant component at two stations of a meridional profile with coordinates x1 and x2 one can find the ratio of their complex spectra:
 | (2) |
Upon a change in frequency
f, the image
R{x(f)} will cover on the
complex plane a certain curve which is a hodograph of the ratio of the
spectra.
This hodograph
has a number of remarkable properties
that make it a quite suitable and informative tool for data
representation. For the time being, we will not be interested in
specific behavior and range of values of
xR(f) we will just assume
that
x=xR covers the entire real axis (Figure 1a). The
right-hand part of formula (2) essentially prescribes a fractional
linear transformation of the complex plane
x. Such a transformation
translates a set of straight lines and circle into the very
same set.
The
pole
(x2 - i e,
e >0) lies below the real axis;
 therefore it is transformed into a circle (Figure 2a), and
in this context, with increasing
x, its image circles this
circle counterclockwise. Note that the circle does
not contain
an origin point
0, since zero and pole
of (2)
the
mapping
lie on one side of the real axis. As is seen from
Figure 1a,
the spectrum ratio argument arg
R equal to the angle of
rotation from the vector representing the denominator to the
numerator vector does not reverse its sign upon a change in
x.
From this and from the fact that
R(
therefore it is transformed into a circle (Figure 2a), and
in this context, with increasing
x, its image circles this
circle counterclockwise. Note that the circle does
not contain
an origin point
0, since zero and pole
of (2)
the
mapping
lie on one side of the real axis. As is seen from
Figure 1a,
the spectrum ratio argument arg
R equal to the angle of
rotation from the vector representing the denominator to the
numerator vector does not reverse its sign upon a change in
x.
From this and from the fact that
R(  )=1, it follows
that the hodograph is tangent to the real axis at point
R=1. The
half plane, wherein lies the hodograph, is determined by the signal
phase difference between the two stations and by the choice of their
ordering in calculating the cross spectra. If the signal at a
station whose spectrum is in the numerator of (2) is lagging in
phase behind the other station, then the hodograph is below the
real axis.
)=1, it follows
that the hodograph is tangent to the real axis at point
R=1. The
half plane, wherein lies the hodograph, is determined by the signal
phase difference between the two stations and by the choice of their
ordering in calculating the cross spectra. If the signal at a
station whose spectrum is in the numerator of (2) is lagging in
phase behind the other station, then the hodograph is below the
real axis.
Let us place on the hodograph a coordinate scale containing certain characteristic values of x. Let x0 be the coordinate of the point that lies exactly in the middle between the stations (x0 =(x1 + x2)/2 ). As is seen from Figure 1a, for a random pair of points x and x' symmetric in relation to x0 , the arguments of corresponding values of R and R' are the same, and the moduli are mutually inverse. This means that the images of these points lie on one secant drawn from the origin 0 (Figure 2a). In particular, this goes for the coordinates of both observatories, x1 and x2. The minimum and maximum values of R are also seen to be symmetric relative to x0. Symmetric points are confluent when x=x'=x0 whereas their images merge when the secant changes into a tangent. Therefore the image of x0 lies on the tangent to the hodograph, drawn from origin 0.
To completely prescribe the circle, its radius r remains to be determined. Let 2 d denote the distance x2-x1 between the stations, and comparing Figures 1b and 2a, we find
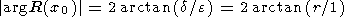 | (3) |
In other words, the angle arg R(x0), at which the hodograph is seen from the origin of coordinates, is equal to the angle at which the interval between the stations is seen from the distance equal to a half width of the resonance. From (3), we find the hodograph radius
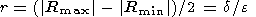 | (4) |
where Rmin and Rmax are the minimum and maximum spectrum ratio values that are attained at points xmin and xmax. Thus the hodograph radius is equal to the distance between the stations expressed in units of the resonance width. This is a clearly visual criterion for determining a situation: large hodographs correspond to narrow resonances or distant stations.
It is seen from Figure 1a that the triangle formed by the numerator
and denominator of
R at
x=x2 differs from half of a similar
triangle at
x=x0 by 2 times increased
cathetus
d This fact
represented in Figure 2a by a doubled cathetus
r in the triangle
with vertices 0 and 1. This means that the image of the coordinate
x2 is diametrically opposite to the image of an
infinite point
 (R=1) and that at
x=x2 there is an extremum of the
imaginary part of the
spectrum ratio
Im
R.
(R=1) and that at
x=x2 there is an extremum of the
imaginary part of the
spectrum ratio
Im
R.
Let us note that the secant that corresponds to the minimum and maximum values of R(f) passes through the hodograph center, whereas the secant corresponding to the positions of the stations passes through the end of diameter connecting R(x2) and 1 (Figure 2a). This means that the interval between the points xmin and xmax contains within itself the interval between the stations. With a monotonic dependence xR(f), from this it follows that the resonance frequencies of the stations always lie between the frequencies corresponding to Rmin and Rmax.
Heretofore, we discussed the hodograph orientation with increasing
x.
This orientation coincides with the orientation with increasing
f if
 xR /
xR / f >0 and is opposite otherwise. Upon a reversal of sign
of the resonance frequency gradient, the sign of
e also
reverses, which in turn results in a reversal of the sense of
covering the hodograph. Thus the hodograph frequency scale is
always counterclockwise.
f >0 and is opposite otherwise. Upon a reversal of sign
of the resonance frequency gradient, the sign of
e also
reverses, which in turn results in a reversal of the sense of
covering the hodograph. Thus the hodograph frequency scale is
always counterclockwise.
As was noted by Gul'el'mi [1989], having simultaneously available frequency dependencies of the amplitude ratio and phase differences at two stations, one can find a continuous dependence of the resonance frequency on the coordinate fR(x). This dependence can also be reconstructed in our approach. To this end, we will use the circle that on the one hand, the spectrum ratio R(x) is determined by formula (2) as a function of coordinate x, and on the other hand, this ratio is known from experiment as a tabulated frequency function. In fact, R(x) is a reversible function of the normalized coordinate X= (x1 -x2)/e
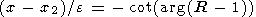 | (5) |
Using relationship (5), one can reconstruct the dependence of resonance frequency on coordinate.
In applications of the gradient method to actual data, there were
situations when the relationship
Rmin Rmax
=1 was not met. A possible cause was assumed to be
the effect of local geology displaying itself in the occurrence of
amplitude and phase distortions specific to each station. To
exclude these distortions,
Green et al. [1993]
proposed a
modified gradient method based on the assumption of independence of
these distortions of frequency.
In our approach, within the assumptions of the
modified gradient method, the complex spectrum ratio acquires an
additional constant complex factor
M . This results in expansion
(contraction) of the hodograph at a coefficient
M and
its rotation at angle
arg M relative to the origin of coordinates
(Figure 2b).
Neither the linear element ratio nor the angular
lengths of arcs between the characteristic points of the hodograph
are affected by this transformation; therefore the majority of the
aforementioned hodograph properties still hold true. The basic
difference is that the hodograph is no longer tangent to the real
axis at
R=1. Instead,
R=M will be the image of
x=  . The sign of
phase lagging between the stations is no longer determined
unambiguously by the half plane wherein the hodograph is found.
However, the phase difference sign can be determined by the
behavior of
arg R(x). For example, if rotation from
R(
. The sign of
phase lagging between the stations is no longer determined
unambiguously by the half plane wherein the hodograph is found.
However, the phase difference sign can be determined by the
behavior of
arg R(x). For example, if rotation from
R(  ) to
R(x0) proceeds clockwise, then the phase difference, after
geology correction, is negative. Also lost is the extremal property
of Im
R for the point representing one of the stations. In order to
determine the value of ( d / e )
from (4), one now must
use, instead of the hodograph radius
r, its "modified" value
(r/ M ).
In addition, the term ( R-M ) will replace ( R-1 ) in
(5). Since in approaching
R(
) to
R(x0) proceeds clockwise, then the phase difference, after
geology correction, is negative. Also lost is the extremal property
of Im
R for the point representing one of the stations. In order to
determine the value of ( d / e )
from (4), one now must
use, instead of the hodograph radius
r, its "modified" value
(r/ M ).
In addition, the term ( R-M ) will replace ( R-1 ) in
(5). Since in approaching
R( ), the conditions of
applicability of initial assumptions are violated and experimental
points drift from the circle, point
R=M may not lie on the real
hodograph. However, to determine
M, one can use the evident
relationships (Figure 2b)
), the conditions of
applicability of initial assumptions are violated and experimental
points drift from the circle, point
R=M may not lie on the real
hodograph. However, to determine
M, one can use the evident
relationships (Figure 2b)
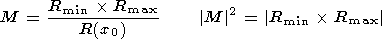 | (6) |
As experience has shown, even an intuitive visual extrapolation of that part of the hodograph which approximates a circle quite well can give a reliable estimate of this coefficient.
The geometric method of analysis of gradient observations is advantageous in that it makes possible a preliminary best-fit approximation for a certain set of frequencies, after which, instead of individual values of R(f) subject to random deviations, one can take values closest thereto that belong to this idealized hodograph. Selection of the frequency range to be used for the construction of the best-fit approximation circle is governed by the following two circles: (1) frequencies far away from the resonance region clearly do not fit the idealized hodograph and are interferences; (2) isolation of a too narrow frequency range within the resonance region makes the hodograph parameters too sensitive to a particular selection of the initial and final frequencies. In practice, estimates of the parameters are stable enough when the selected frequency range turns out to be of the same order of magnitude as the difference of frequencies corresponding to Rmin and Rmax. If the distance between the stations is known, then one can, switching from normalized to conventional coordinates and using the ratio ( d / e ) defined from the radius of best-fit hodograph obtain the resonance width and the Q factor of the resonator.
Oscillations in the Pc4 range were detected at five stations of a United Kingdom meridional network: (1) ( F =62.5o ), (2) ( F =60.0o ), (3) ( F =58.9o ), (4) ( F =57.1o ), and (5) ( F =54.6o ). The extreme northern and southern stations had a rather low signal; therefore, data from these stations should be treated with caution. Amplitude and phase spectra at each station were calculated using the Fourier transform and then smoothed with the aid of a five-point running average. The network of stations is described in detail by Green [1978], and a general view of the spectra can be found in the papers by Baranskiy et al. [1988] and Fedorov et al. [1989].
 The spectrum ratio hodographs were calculated using a specially
developed program making it possible to interactively determine the
values of resonance frequencies
f1= fR(x1),
f2= fR(x2),
fA= fR(x0),
and the
Q factor.
Stability of the
results
obtained
was monitored by (1) varying the
length of the spectral interval wherein appropriate points fit
the circle
well
and (2) changing to the inverse ratio
R-1 (f).
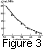
Figure 3
shows the results of calculations of resonance frequencies
fR( F ) for
each pair of stations. For comparison, Figure 3
shows by circles the values of resonance frequencies
fA( F) of the
field lines running between the stations, determined by the
standard gradient method
[Baranskiy et al., 1988].
This
method is seen to give somewhat underestimated (by 1 mHz
on average) values of local resonance frequencies. This
discrepancy is attributed to the fact that
Baranskiy et al. [1988]
did not introduce in their calculations the amplitude and phase
correction coefficients amounting for this profile to
M =0.9
The spectrum ratio hodographs were calculated using a specially
developed program making it possible to interactively determine the
values of resonance frequencies
f1= fR(x1),
f2= fR(x2),
fA= fR(x0),
and the
Q factor.
Stability of the
results
obtained
was monitored by (1) varying the
length of the spectral interval wherein appropriate points fit
the circle
well
and (2) changing to the inverse ratio
R-1 (f).
Figure 3
shows the results of calculations of resonance frequencies
fR( F ) for
each pair of stations. For comparison, Figure 3
shows by circles the values of resonance frequencies
fA( F) of the
field lines running between the stations, determined by the
standard gradient method
[Baranskiy et al., 1988].
This
method is seen to give somewhat underestimated (by 1 mHz
on average) values of local resonance frequencies. This
discrepancy is attributed to the fact that
Baranskiy et al. [1988]
did not introduce in their calculations the amplitude and phase
correction coefficients amounting for this profile to
M =0.9 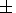 0.2 and
arg M=10
0.2 and
arg M=10  5o.
5o.
It should be noted that the resonance frequencies of a particular station, calculated by the hodograph method in tandem with a northern or southern station, differed on average by 0.2-0.5 mHz. This difference (clearly seen in Figure 3 between greatly spaced stations) displays itself in small jumps in fR( F ) at latitudes of the stations. This discrepancy seems to be associated with the occurrence of asymmetry of the resonance amplitude curve in receding from the resonance point: the northern slope becomes steeper than the southern one, which is ignored by the main leading (1) of the asymptotic expansion of the wave field in the resonance region [Fedorov et al., 1989].
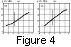 As was mentioned above, the described approach makes it possible
not
only to determine the discrete values of resonance frequencies at
characteristic points, but also to reconstruct the
continuous latitudinal
distribution of
fR( F ).
Figures 4a
and 4b
show examples of restoration of the resonant
frequency dependence
fR(X) on the normalized distance
X=(x-x2)/e for
station pairs 2/3 and 3/4.
The station positions correspond to points
X=0 and
X=(x1-x2)e,
the latter is being marked
by vertical bar. Note that
the hodograph method enables
us to restore the distribution
fR(X) not only between the
stations, but even in a latitude range beyond this interval.
As was mentioned above, the described approach makes it possible
not
only to determine the discrete values of resonance frequencies at
characteristic points, but also to reconstruct the
continuous latitudinal
distribution of
fR( F ).
Figures 4a
and 4b
show examples of restoration of the resonant
frequency dependence
fR(X) on the normalized distance
X=(x-x2)/e for
station pairs 2/3 and 3/4.
The station positions correspond to points
X=0 and
X=(x1-x2)e,
the latter is being marked
by vertical bar. Note that
the hodograph method enables
us to restore the distribution
fR(X) not only between the
stations, but even in a latitude range beyond this interval.
As was noted above, the hodograph
method
also
makes it possible
to
determine the
QA factor of the magnetospheric Alfvén resonator.
It should be kept in mind that the
Q factor of Alfvén oscillations
observed on the ground comprises the contribution of the effects of
phase mixing and spatial integration
[Yumoto et al., 1995].
The magnetospheric resonator
Q factor values
QA 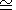 6
6 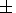 3 calculated considering this circumstance correspond to the values
of a model of the ionospheric dissipation of the fundamental mode of
Alfvén field line oscillations
[Yumoto et al., 1995].
3 calculated considering this circumstance correspond to the values
of a model of the ionospheric dissipation of the fundamental mode of
Alfvén field line oscillations
[Yumoto et al., 1995].
A visual geometric method of analysis of pulsation observations at a meridional profile of stations has a number of advantages compared with the standard gradient method. The new approach based on the construction of a hodograph of complex spectrum ratio allows a visual check of the degree of fit of experimental data to a theoretical model in the entire frequency range. Accordingly, calculations of parameters of the resonance structure are carried out by least-square approximation of a curve in a finite frequency range and not by one characteristic point of the spectrum, as in the gradient method. As a result, the results produced by the hodograph method turn out to be more stable. Besides, this method has additional potentialities compared with the standard gradient method. Measurements at two points can provide the following: (1) not only the resonance frequency of the median field line, but also local resonant frequencies of the observation points themselves; (2) the Q factor of the magnetospheric Alfvén resonator; and (3) continuous distribution of resonance frequencies in a finite latitude range beyond the latitudes of the observation points.
Baranskiy, L. N., Yu. E. Borovkov, M. B. Gokhberg, and S. M. Krylov, A gradient method of measurement of resonance frequencies of field lines, Izv. Akad. Nauk SSSR Fiz. Zemli (in Russian), 8, 74, 1985.
Baranskiy, L. N., S. P. Belokris, Yu. E. Borovkov, M. B. Gokhberg, E. N. Fedorov, and C. A. Green, A gradient method of reconstruction of the meridional structure of geomagnetic pulsation field, Dokl. Akad. Nauk SSSR (in Russian), 229, 1347, 1988.
Best, A., S. M. Krylov, Yu. P. Kurchashov, and V. A. Pilipenko, A gradient temporal analysis of the Pc3 pulsations, Geomagn. Aeron. (in Russian), 26 (6), 980, 1986.
Fedorov, E. N., et al., Diagnostics of the magnetospheric plasma density from gradient observations of geomagnetic pulsations, Izv. Akad. Nauk SSSR Fiz. Zemli (in Russian), 12, 63, 1989.
Green, A. W., E. W. Worthington, L. N. Baransky, E. N. Fedorov, N. A. Kurneva, V. A. Pilipenko, D. N. Schvetzov, A. A. Bektemirov, and G. V. Philipov, Alfvén field line resonances at low latitudes ( L=1.5 ), J. Geophys. Res., 98A (9), 15,693 1993
Green, C., Meridional characteristics of Pc4 micropulsations event in the plasmasphere, Planet. Space Sci., 39, 569, 1978.
Gul'el'mi, A. V., Hydromagnetic diagnostics and geoelectric prospecting, Usp. Fiz. Nauk (in Russian), 158, 605, 1989.
Pilipenko, V. A., and E. N. Fedorov, Magnetotelluric sounding of the crust and hydromagnetic monitoring of the magnetosphere with the use of ULF waves, Annali di Geofisica, 36 (5-6), 19, 1993.
Pilipenko, V. A., T. A. Povzner, I. V. Savin, and Ya. S. Nikomarov, Local spatial structure of the geomagnetic pulsation field at middle latitudes, Izv. Akad. Nauk SSSR Fiz. Zemli (in Russian), 10, 54, 1988.
Yumoto, K., V. Pilipenko, E. Fedorov, N. Kurneva, and K. Shiokawa, The mechanisms of damping of geomagnetic pulsations, J. Geomag. Geoelectr., 47 (2), 163, 1995.
Waters, C. L., F. W. Menk, and B. J. Fraser, Phase structure of low latitude Pc3-4 pulsations, Planet. Space Sci., 39, 569, 1991.