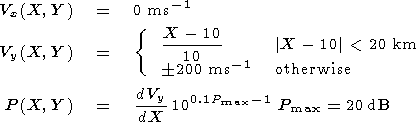International Journal of Geomagnetism and Aeronomy
Vol 2, No. 1, June 2000
On the factor conditioning
the Doppler spectral width determined from SuperDARN HF radars
R. André and M. Pinnock
British Antarctic Survey,
Natural Environment Research Council,
Cambridge,
UK
J.-P. Villain
Laboratoire de Physique et Chimie de l'Environnement,
Centre National de la Recherche Scientifique,
Orléans Cedex, France
C. Hanuise
Laboratoire de Sondage de l'Environnement Electromagnétique
Terrestre, Centre National de la Recherche Scientifique, Université
de Toulon et du Var,
La Garde Cedex, France
Contents
Abstract
The SuperDARN radars are proving
to be a very powerful experimental tool for
exploring solar wind-magnetosphere-ionosphere
interactions. They measure the autocorrelation
function (ACF) of the transmitted signal backscattered from ionospheric
irregularities, and derive parameters such as the Doppler velocity and
spectral width. This paper reviews the physical origin of the spectral
width and the factors which can affect it, such as micro-scale
ionospheric turbulence, low-frequency wave activity and gradients
which occur naturally in the polar ionosphere.
1. Introduction
SuperDARN is a network of HF radars which determines amongst other things,
the large-scale convection pattern in a plane perpendicular to the magnetic
field
[Greenwald et al., 1985]
over the ionospheric auroral zone. From the transmission
of a multiple pulse scheme,
the radars measure the autocorrelation
(ACF) of the signal backscattered at
several distances (range gates) from
the radar by field-aligned concentration
irregularities. For each range gate, this ACF is routinely analyzed by
a basic method (FITACF)
[Baker et al., 1995;
Villain et al., 1987]
which extracts the power,
the line-of-sight Doppler velocity of the irregularities and the spectral
width. This Doppler spectral width is a measure of ionospheric plasma
turbulence caused by the structured
energetic precipitation or by electric
field variations within each range-beam cell of the radar.
Baker et al. [1990, 1995],
and
Rodger et al. [1995]
have shown
that the radar spectral width, and more generally the ACF
characteristics have some particular properties inside the cusp.
They have used low-altitude satellite data and optical imagers to show
that HF data recorded in the cusp are characterized by a high-spectral
width. Several studies have used this parameter to identify the cusp,
and to derive more information about solar wind-magnetosphere-ionospheric
coupling, such as the temporal evolution
of the reconnection rate at the magnetopause
[Baker et al., 1997;
Pinnock et al., 1999].
Recently,
André et al. [1999]
have shown that wave activity in the Pc1 frequency
band can explain all the ACF characteristics observed in the cusp.
On the nightside, some studies have related the increase of spectral
width with latitude with the central plasma sheet (CPS)/boundary
plasma sheet (BPS) boundary
[Dudeney et al., 1998].
This property has been
used to observe the boundary motion during substorm events
[Lewis et al., 1997].
Few studies have explored the physical processes which
give rise to the spectral width.
Grésillon et al. [1992],
Hanuise et al. [1993]
and later
Villain et al. [1996]
have applied
collective scattering theory to the HF radar data.
They have shown that the shape of the ACF power
variation and its spectral width are related to
characteristics of the turbulent motion of density irregularities.
In this paper, we review the physical origin of the radar spectral
width, and discuss factors that can affect it. The next section
presents a general view of the spectral width behavior from a
statistical point of view. The third part discusses the link
between the spectral width and the micro-scale ionospheric
turbulence and makes some comments about the interaction
between radar waves and field-aligned irregularities. The
effect of wave activity routinely seen by low-altitude
satellites will be examined
in the fourth section. The
next two sections evaluate
the impact of the large-scale
convection pattern, and the
effect of meso-scale inhomogeneities,
like vortices, which can be present in
the convection. The last part summarizes
these effects and their
importance in our understanding of the spectral width measured by HF radars.
2. Data Overview
To have a global view of the spectral width over the whole polar ionosphere,
we have conducted a statistical study. We have built a large database, compiled
from northern hemisphere radar data recorded between October 1996 and March
1997. This database contains only ionospheric scatter from the
F region
selected by its range (900 km
< range
< 3300 km) and characterized
by a large signal-to-noise ratio ( > 3 dB). These data are localized in
a grid defined in MLT (Magnetic Local Time) and MLAT (Magnetic Latitudes)
which has a resolution of 30 minutes and 1o, respectively.
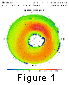 Figure 1 shows the average spectral width observed in the low-altitude
ionosphere by HF radars in the northern hemisphere. Its main characteristic
is that the spectral width is low at low latitudes and inside the polar cap
(
Figure 1 shows the average spectral width observed in the low-altitude
ionosphere by HF radars in the northern hemisphere. Its main characteristic
is that the spectral width is low at low latitudes and inside the polar cap
( 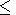 150 m s
-1 ), but increases up to 200 m s
-1 in the auroral
oval, and is at a maximum inside the cusp
( > 250 m s
-1 ). These results
have been determined before
(J. P. Villain and R. A. Greenwald, unpublished data, 1994)
using a similar statistical database. A more
detailed presentation of these two statistical studies
is the subject of a forthcoming paper
[Villain et al., manuscript in preparation, 1999].
Here, the physical mechanisms that lead to these high-spectral
widths are reviewed and discussed.
150 m s
-1 ), but increases up to 200 m s
-1 in the auroral
oval, and is at a maximum inside the cusp
( > 250 m s
-1 ). These results
have been determined before
(J. P. Villain and R. A. Greenwald, unpublished data, 1994)
using a similar statistical database. A more
detailed presentation of these two statistical studies
is the subject of a forthcoming paper
[Villain et al., manuscript in preparation, 1999].
Here, the physical mechanisms that lead to these high-spectral
widths are reviewed and discussed.
3. Micro-Scale Turbulence
The spectral width is usually described
in terms of turbulent processes and
instability mechanisms. It arises from
interactions between irregularities, or from micro-scale electric fields.
3.1. Background
In this description, we assume that all irregularities are moving with a
large-scale velocity
V0, and have a random displacement
d due to this micro-scale electric field.
The signal
backscattered by the electron density irregularities
can be written as equation (1), where
G( k) is the form factor which mainly depends
on the number of
irregularities and their amplitude
[Grésillon et al., 1992].
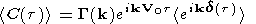 | (1) |
The ACF phase is controlled by the second term,
and gives access to the line-of-sight Doppler velocity.
The last term, which determines the spectral width,
is the Fourier transform of the probability distribution
of irregularity displacement during the
time
t ( P(d, t) ),
and is also called the statistical characteristic.
It depends on statistical properties of the micro-scale
displacements
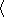 kd(t)
kd(t) 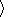 . The
average expressed by the brackets is taken over the
whole range gate and integration time (typically 7 s).
In equation (1), the second term refers to large-scale
processes (greater than a range-beam cell) and the third
one to micro-scale processes (size of the irregularities).
. The
average expressed by the brackets is taken over the
whole range gate and integration time (typically 7 s).
In equation (1), the second term refers to large-scale
processes (greater than a range-beam cell) and the third
one to micro-scale processes (size of the irregularities).
3.2. Application to Coherent HF Radar
Grésillon et al. [1992]
and
Hanuise et al. [1993]
consider the limiting cases
where the correlation length of the irregularity motion is
in turn much shorter and much longer than the observation
wavelength, to derive
P(d, t)
and thus derive the ACF
power. When this correlation length is much shorter than the radar wavelength,
P(d, t)
can be represented by a random walk and hence a
Gaussian function. The resulting ACF
power is an exponential function characterized by a decay which is
mainly controlled by a diffusion coefficient.
Grésillon et al. [1992]
have
estimated this diffusion coefficient in a tokamak and found a very
good agreement with those estimated by the classical
method. In the other limit, the displacement depends linearly on the
velocity. Under the assumption that the velocity distribution function
is Gaussian, they obtained the usual Gaussian Doppler spectrum which
depends on the microscopic velocity fluctuations
observed during the integration process.
Hanuise et al. [1993]
have
already shown that the ACF power variation observed in HF radar
data has these shapes, but more often has an intermediate state,
with an ACF starting with a Gaussian shape and ending with an
exponential one.
Extending this study to a more general case,
Cabrit [1992],
followed by
Villain et al. [1996],
have derived the general analytical function
under the assumption of a Gaussian distribution
function
P(d, t).
This general function, displayed in
equation (2), depends on both the diffusion coefficient ( D ) and the
correlation time of irregularity motions ( T ).
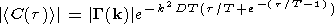 | (2) |
 These last two parameters can be estimated by fitting equation
(2) to ACFs observed by HF radars. Figure 2 shows a typical
example of the temporal evolution of the ACF power recorded
at the Halley station in the southern hemisphere. The best fit is shown
by the line, and uses a diffusion coefficient,
D, and a correlation time,
T, of 90 m
2 s
-1 and 5.5 ms, respectively. The spectral width
determined by FITACF is 125 m s
-1. This function represents well
the recorded data, with a Gaussian decay
on the first lags and an exponential decay on the last ones.
These last two parameters can be estimated by fitting equation
(2) to ACFs observed by HF radars. Figure 2 shows a typical
example of the temporal evolution of the ACF power recorded
at the Halley station in the southern hemisphere. The best fit is shown
by the line, and uses a diffusion coefficient,
D, and a correlation time,
T, of 90 m
2 s
-1 and 5.5 ms, respectively. The spectral width
determined by FITACF is 125 m s
-1. This function represents well
the recorded data, with a Gaussian decay
on the first lags and an exponential decay on the last ones.
3.3. Towards an Estimation of the Diffusion Coefficient
By making a large statistical study of the diffusion coefficient
values in the auroral
F region,
André et al. [1998]
showed that its
distribution function is frequency dependent. Its maximum is found
around 100 m
2 s
-1 and 400 m
2 s
-1 for radar
frequencies of 12 and 9 MHz, respectively. More precisely,
they have shown that the distribution functions obtained with
a radar frequency above 11 MHz are very similar, whereas the increase
in diffusion coefficient occurs for frequencies below 10 MHz.
A diffusion coefficient of 100 m
2 s
-1 is comparable
to the Bohm diffusion coefficient in the
F region (125 m
2 s
-1 ),
and to the ion cross
B field diffusion coefficient in the collisional
E region, but is much higher than the typical ambipolar
diffusion coefficient (1 m
2 s
-1 ). This suggests
an overestimation of
D in the
F region.
At low radar frequencies,
André et al. [1998]
showed that this distribution depends also
on the length of the radar wave propagation path.
This suggests an interaction between the radar wave
and the field-aligned irregularities in the ionosphere. This
interaction decreases the wavefront coherence during its
propagation, and so artificially increases the spectral width.
These studies have shown a clear correspondence between the
spectral width and micro-scale turbulent processes. They
have estimated some typical values of the turbulent transport
experienced by ionospheric irregularities which have a wavelength around 10 m.
Although the ACF shapes agree well with their theoretical counterparts, the
estimated diffusion coefficient is higher than the expected values. This
suggests that some other effects contribute to spectrum broadening.
4. Time-Varying Electric Field
4.1. Wave Activity in the Cusp
Baker et al. [1995]
have shown a clear correspondence between high spectral
width and the particle signature of the low-altitude cusp. Figure 1
shows that, on average, spectral width values in the cusp, centered
at about
73o and 11 MLT, are higher than 250 m s
-1.
More precisely, spectra recorded inside the cusp contain several
components, and both the velocity and spectral width determined
by FITACF are highly variable
[Baker et al., 1995;
Pinnock et al., 1995].
As observed by low-altitude satellite, the cusp region
is characterized by a sharp increase in low frequency
wave activity (0.1-10 Hz)
[Erlandson and Anderson, 1996;
Matsuoka et al., 1993].
A
part of these electric and magnetic field variations
arises from field-aligned currents. However,
a significant component arises from a mixture
of downgoing and upgoing Alfvén waves.
These waves are generated at the dayside magnetopause,
during reconnection processes or by the upgoing accelerated ions
at the poleward edge of the cusp
[e.g. Dyrud et al., 1997].
Their amplitudes are sufficiently high (a few mV m
-1 )
to modulate the large-scale velocity field and hence generate
temporal variations of the macroscopic contribution to the ACF in
equation (1).
4.2. Impact of the Wave Activity on the
Spectral Width in the Cusp
 Recently,
André et al. [1998]
have evaluated the effect of such electric field
variations on the ACF recorded by HF radars. They have simulated this
effect on the radar data, under the assumption that there is no turbulence
in the ionosphere: The expected ACF
power variation should have no decay
because all the irregularities are always
totally correlated. Figure 3 shows an
example of their simulation. The upper
panels show the electric field spectrum (left) and the corresponding
temporal variation of the velocity field (right).
The lower panels show the temporal evolution of
the ACF phase (left) and ACF power (right). The
dashed line shows the expected ACF without the wave.
Here, the plasma is moving with a constant velocity of
100 m s
-1, modulated by a wave characterized
by an amplitude of 40 ms
-1 and a frequency of 0.5 Hz.
Recently,
André et al. [1998]
have evaluated the effect of such electric field
variations on the ACF recorded by HF radars. They have simulated this
effect on the radar data, under the assumption that there is no turbulence
in the ionosphere: The expected ACF
power variation should have no decay
because all the irregularities are always
totally correlated. Figure 3 shows an
example of their simulation. The upper
panels show the electric field spectrum (left) and the corresponding
temporal variation of the velocity field (right).
The lower panels show the temporal evolution of
the ACF phase (left) and ACF power (right). The
dashed line shows the expected ACF without the wave.
Here, the plasma is moving with a constant velocity of
100 m s
-1, modulated by a wave characterized
by an amplitude of 40 ms
-1 and a frequency of 0.5 Hz.
This example shows that the temporal evolution of both
the phase and the power are modulated. This implies that
the associated spectrum contains more than one component,
as recorded in the cusp. The power decays despite the fact
that there are no turbulent processes included in this simulation.
If the velocity deduced by FITACF is representative of the input
field, then the spectral width obtained is very high, greater than
300 m s
-1. They have also shown that under these
conditions, and even with a low-amplitude wave, the velocity
and spectral width determined from these ACFs are highly
variable, and that the spectral width is very high.
To produce a high-spectral width, the wave amplitude
has to be greater than a threshold which is frequency
dependent
(R. André et al., Identification of the
low altitude cusp by SuperDARN radars: A physical explanation
for the empirically derived signature, Submitted to
J. Geophys. Res., Nov. 1999,
hereinafter referred to as André, 1999).
For example, the minimum value is 20 ms
-1 (which corresponds
to an electric field amplitude of 1 mV m
-1 ) at 0.5 Hz, and only
2 m s
-1 (0.1 mV m
-1 ) at 5 Hz.
These amplitudes are low
compared to those usually recorded by satellites
[Maynard et al., 1991].
All the waves which have a frequency lower than the Nyquist
frequency (4 mHz in the common radar's running mode, and 50 mHz
in the high-resolution mode) are correctly resolved by the radar,
but the highest frequency waves are undersampled
(André, 1999).
In this case, the Doppler spectrum contains several components.
These supplementary components are caused by the radar technique
and are artefacts. At last, These results are independent
of the background line-of-sight velocity
(André, 1999).
4.3. Extension to Elsewhere in the Auroral Oval
Low frequency wave activity is also observed along magnetic
field lines in the auroral oval
[Gurnett, 1991].
Hence, one
can probably use the same mechanism to explain the high
spectral widths found over the whole auroral oval (see
Figure 1),
and especially in the nightside where a smooth
increase of the spectral width has been found together
with both the central plasma sheet/boundary plasma sheet
boundary layer and with an increase in the wave activity
[Dudeney et al., 1998].
Following
Gary et al. [1998],
this wave activity over the auroral zone could
be the signature of boundaries in the large-scale field-aligned current
system. Therefore, because low-frequency waves (0.1-10 Hz) strongly
perturb the ACF, leading to multi-component spectra and very high
spectral width, one can probably use these characteristics to map
boundaries of the large-scale current system, however rigorous
testing of this idea has yet to be carried out.
5. Large-Scale Convection Pattern
5.1. Impact
The large-scale plasma motion at high latitudes
is driven by the solar wind-magnetosphere-ionosphere
system, and is usually composed of two, three or four
cells depending on the interplanetary magnetic field
orientation
[Cowley and Lockwood, 1992].
This ionospheric convection
results in several gradients in the velocity field over
the whole auroral oval, which are sufficiently sharp to
affect the velocity distribution experienced by the irregularities.
For example, one can expect that inside a convection reversal, one
part of a radar range gate is sensitive to an electric field
directed in one direction whereas the other part is mainly
dominated by an electric field directed in the opposite direction.
Thus, the measured ACF should reflect these two different velocities,
and the spectrum should contain two components. Because the FITACF
method is not well adapted to these kind of ACFs, the computed spectral
width is expected to be higher.
Such a situation regularly appears in the radar data. For example,
Barthes et al. [1998]
have applied the high-resolution spectral analysis
method MUSIC (MUltiple SIgnal Classification) to radar data. They
have found that the probability of finding multi-component
spectra is strongly enhanced in convection reversals.
5.2. Estimated Spectral Width
By considering a realistic convection model
[e.g. Rich and Maynard, 1989]
derived from
Heppner and Maynard [1987],
one can assign an electric field
vector to each point in the high latitude ionosphere. One can
also define a grid in a given radar range gate which has a spatial
resolution (1 km) much smaller than the gate dimensions (45 km long,
100 km wide on average). Thus, at any particular time, one can compute
the line-of-sight velocity at each grid point,
and then compute the velocity distribution found over the whole
range gate. Assuming there is no turbulent effect, the ACF spectrum
should reflect this distribution, and thus its width should be the
spectral width recorded by the radar. Thus, at one particular time
and for a given range gate, one can estimate the spectral width
induced by the large-scale ionospheric convection pattern.
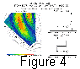 Figure 4 (left panel) shows the estimated spectral width
in the Stokkseyri radar field of view at 1900 UT. At this
time, the radar is looking mainly at the convection reversal.
Black lines represent isocontours of the convection model
defined by
Rich and Maynard [1989].
Two examples of the computed
velocity distribution are also
shown. When the radar is looking in
a region where there is no large velocity
gradient (upper right panel), the velocity
distribution is narrow, and the associated spectral width is negligible.
By contrast, when this range gate is inside a large velocity gradient
(lower right panel), the spectral width can be as large as 250 m s
-1.
Figure 4 (left panel) shows the estimated spectral width
in the Stokkseyri radar field of view at 1900 UT. At this
time, the radar is looking mainly at the convection reversal.
Black lines represent isocontours of the convection model
defined by
Rich and Maynard [1989].
Two examples of the computed
velocity distribution are also
shown. When the radar is looking in
a region where there is no large velocity
gradient (upper right panel), the velocity
distribution is narrow, and the associated spectral width is negligible.
By contrast, when this range gate is inside a large velocity gradient
(lower right panel), the spectral width can be as large as 250 m s
-1.
One can also see that the distribution shown in the lower right hand panel
is not totally flat but has a minimum value near 0. If the velocity gradient
increases in this convection reversal, one can expect a better separation
between the positive and negative values of the velocity. Then, one can
obtain a clear multi-component spectrum. Despite the fact that this
ionospheric convection model is based on a representative description
of the real convection pattern
[Heppner and Maynard, 1987],
it smoothes the velocity
gradients. Thus one can conclude that convection reversals can naturally
introduce some multi-component spectra, and that they should induce a
high spectral width value.
Because the radar records only the line of sight velocity
( k  v ), the results presented
in Figure 2
can be different when looking in the same geophysical region
with another radar. For example, when considering a radar
which is mainly looking poleward, the gradients will be smaller,
even in the convection reversal. In this case, the deduced spectral
width is also much smaller.
v ), the results presented
in Figure 2
can be different when looking in the same geophysical region
with another radar. For example, when considering a radar
which is mainly looking poleward, the gradients will be smaller,
even in the convection reversal. In this case, the deduced spectral
width is also much smaller.
We have estimated the contribution of the convection pattern
to the
spectral width by using the statistical ensemble (radar/beam/gate)
found in Figure 1.
Because radars in the northern hemisphere have
different orientations with respect to a magnetic coordinate system,
and most of them are oriented northward, the maximum spectral width
found in the convection reversals has a value of only 150 m s
-1.
In other geophysical regions, the spectral width is lower than
50 m s
-1.
This clearly shows that this effect cannot be used
to explain the high spectral values recorded in the cusp and along
the auroral oval, and even at low latitudes where spectral width is
of the order of 150 m s-1
(see Figure 1).
One can conclude that velocity gradients induced
by the large-scale convection pattern can affect
the radar spectral width. This effect becomes
important when the gradient is orthogonal to the
radar beam direction, but it cannot be used to explain the spectral
width usually recorded by the HF radars.
6. Meso-Scale Inhomogeneities
If the ionospheric convection leads to large-scale
velocity gradients ( 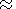 100 km), specific
events in the solar wind-magnetosphere-ionosphere
system can induce smaller-scale perturbations in
the ionospheric convection, such as flux transfer events or
travelling convection vortices. To clearly evaluate their
effects on the ACF, we have conducted a realistic simulation
of the radar processing technique. We first apply the simulation to a
velocity shear that could be induced by either a large-scale
convection reversal, as shown previously, or by an auroral arc.
Secondly, the simulation is applied to meso-scale vortices (
100 km), specific
events in the solar wind-magnetosphere-ionosphere
system can induce smaller-scale perturbations in
the ionospheric convection, such as flux transfer events or
travelling convection vortices. To clearly evaluate their
effects on the ACF, we have conducted a realistic simulation
of the radar processing technique. We first apply the simulation to a
velocity shear that could be induced by either a large-scale
convection reversal, as shown previously, or by an auroral arc.
Secondly, the simulation is applied to meso-scale vortices ( 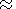 10 km).
10 km).
6.1. Methodology
To evaluate more precisely the ACF resulting from meso-scale inhomogeneities
in one range gate, we have to write equation (1) as (3), where
Pj is the backscattered power from a single irregularity,
Vj is
its velocity,
r0j+ d rj is its
initial position, and where the average is made over
the integration time, which represents about 65 individual ACFs.
 | (3) |
To simplify this description, we remove turbulent effects
(first term of (3)), and define a velocity profile onto a
grid
r0j which has a spatial resolution of 2 km.
The defined range gate is 45 km long and 90 km wide, and corresponds to
a
gate located at about 1500 km from the radar.
To take into account the various positions of the scatterers, we have
applied a small perturbation
d r0j to their initial
position on the grid. This perturbation is linked to the fact that
during two successive individual ACFs, the irregularities have
moved, producing a phase shift in (3) which can be simulated by
a small random number which has a maximum value of 10 meters,
much smaller than the grid resolution (2 km). One has to note that
this initial perturbation does not vary during the
construction of each individual ACF and thus cannot
be compared to the displacement due to turbulent
processes
d(t).
Finally, the power
Pj is linked to the irregularity
backscattering cross section, their number and amplitude.
The backscattering cross section depends on the geophysical
conditions which give rise to the irregularities and should increase in their
source region.
The grid coordinates are defined such that the directions parallel and
perpendicular to the wavevector are in the
Y and
X directions, respectively.
The center of this coordinate system corresponds to the gate center.
6.2. Velocity Shear
The first application is a velocity shear, which may result from a
more realistic large-scale convection pattern, i.e., with a sharper
gradient. In this example, the velocity shear is defined by (4) and
is superimposed on a background velocity of 50 m s
-1 in
both the
X and
Y direction. The backscattered power associated
with the plasma outside the structure is 3 dB
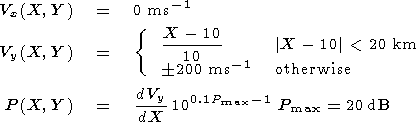 | (4) |
 Figure 5a shows the resulting velocity vectors of the plasma
flow and the backscattered power coded in gray scale. Most
power is defined to come from the velocity shear itself;
the velocity shear instability
[Kintner, 1976]
can increase
both the irregularity number and their amplitude. In this simulation,
the maximum power due to this gradient is defined to
be 20 dB. One has to note that ACF characteristics
do not strongly depend upon this arbitrary value.
Figure 5a shows the resulting velocity vectors of the plasma
flow and the backscattered power coded in gray scale. Most
power is defined to come from the velocity shear itself;
the velocity shear instability
[Kintner, 1976]
can increase
both the irregularity number and their amplitude. In this simulation,
the maximum power due to this gradient is defined to
be 20 dB. One has to note that ACF characteristics
do not strongly depend upon this arbitrary value.
Figures 5b and 5c show the temporal evolution of
the ACF phase and power as deduced by this simulation.
The FITACF method gave a line-of-sight velocity of
120 m s
-1 and a spectral width of 170 m s
-1.
This value is high despite no turbulent effects being included
in this simulation.
The dashed line shows the temporal evolution of the ACF phase
which corresponds to this velocity. Although a general agreement
is found, the simulated phase shows a non linear behavior which
cannot be fully reproduced by the FITACF method. Because this
modulation is also seen in the power, the spectrum associated
with this ACF contains more than one component. This result is
similar to that found by
Barthes et al. [1998],
who showed an increase
in the probability of finding several components (in the velocity
spectrum) inside a convection reversal.
6.3. Vortex
In this part, we simulate the effect of a filamentary field aligned
current (of the order of the range/beam cell)
[Borovsky, 1993].
The
current closure in the conducting layer will generate a divergent
electric field structure, and hence a small-scale vortex.
A vortex in a plane perpendicular to the magnetic field can
be described by equation (5)
[e.g. Pudovkin et al., 1997],
where
r is the distance from the vortex center, defined at
(X,Y)=(-5,-5), normalized over the radius of a charged cylinder (10 km).
The background
velocity is directed in the
Y direction, with an amplitude of
50 m s
-1.
 | (5) |
Depending of its direction, the current that sustains the vortex
can generate irregularities by the current convective instability
[Ossakow and Chaturvedi, 1979]
and thus could increase the backscattered power in
the vortex center.
 The resulting plasma flow and the phase and power of the
recorded
ACF are shown in Figures 6a, 6b and 6c, respectively. Again, the
phase does not present a linear behavior, the power is characterized
by a very high spectral width, and both suggest a multi-component spectrum.
The resulting plasma flow and the phase and power of the
recorded
ACF are shown in Figures 6a, 6b and 6c, respectively. Again, the
phase does not present a linear behavior, the power is characterized
by a very high spectral width, and both suggest a multi-component spectrum.
Applying a high-resolution spectral analysis method (maximum entropy) to the
radar data,
Schiffler et al. [1997]
have found a large number of double-peaked spectra
in the low latitude boundary layer (LLBL). They suggested that these
double-peaked spectra could arise from filamentary currents
generated
by structured soft electron precipitation
( E 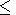 100 eV) observed
by satellites at the same time. These currents could generate
small-scale vortices (scale size of around 10 km), such as the
one shown in Figure 6a.
100 eV) observed
by satellites at the same time. These currents could generate
small-scale vortices (scale size of around 10 km), such as the
one shown in Figure 6a.
The non-linearity seen in the phase is reduced when decreasing
either the maximum velocity in the vortex center or the vortex
size. For example, a vortex that has a typical size less than
5 km does not generate a clear multi-component spectrum in the radar
data. On the other hand, structured precipitation might generate a
series of vortices in the radar gate, which would strongly increase
the non-linearity, but would not necessarily generate a double-peaked
spectrum; they would more likely generate a spectrum that has
more than 2 components.
7. Conclusion
We have described, through simulations, a number of factors which
condition the line-of-sight Doppler spectral width as determined
by SuperDARN HF radars.
The spectral width is related to microscopic properties of the
displacement of irregularities resulting from a turbulent electric
field. More precisely, the ACF power is linked to the correlation
time of the irregularity motion and typical diffusion coefficient.
This is supported by the observed shape of the ACF power variation.
The estimated diffusion coefficient in the ionospheric
F region is
found to be of the order of the maximum diffusion allowed
in a magnetized plasma (Bohm diffusion). This very high value
suggests it is an overestimation. Therefore, although the
microscopic physics can provide the main contribution to
the spectral width, there are other factors which can be equally important.
When the radar frequency approaches the typical plasma frequency in the
ionosphere, the radar wavefront can interact with field-aligned
irregularities. This results in a decrease of the wavefront
coherence and hence an apparent increase of the measured spectral width.
This interaction is supported by the increase in the diffusion coefficient
when both the radar frequency is low and the distance from the radar increases.
Considering meso-scale contributions to the spectral width, simulations indicate
that any inhomogeneities in the velocity flow in the probed area would
increase
the spectral width. Moreover, this can easily introduce several components in
the recorded spectrum. Because the analysis method that is used to derive the
spectral width (FITACF) is not well adapted to these spectra, the resulting
spectral width will be overestimated. Such multi-component spectra have
already been found in large-scale velocity
shears and in the dayside ionosphere. Such
an effect can also be achieved by taking
into account temporal variations of the
large-scale electric field. In this situation,
the velocity spectrum is expected to have
several components, and the recorded spectral width
should be very high and variable. These characteristics
are routinely observed when the radar is probing the ionospheric cusp.
Thus, we have demonstrated that the Doppler spectral width determined
by the SuperDARN HF radars is a complex convolution of
(i) Pc1/Pc2 wave activity,
(ii) geometry of the radar with respect to the large scale convection pattern,
(iii) the presence of velocity shears of the scale size of a range/beam cell
and
(iv) the microscale turbulence ( 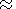 10 m).
We have shown that wave activity is the dominant
parameter in areas such as the cusp. At other
longitude and magnetic local times the other
three effects make a significant contribution.
10 m).
We have shown that wave activity is the dominant
parameter in areas such as the cusp. At other
longitude and magnetic local times the other
three effects make a significant contribution.
Acknowledgments
This work
has been funded by European Community grant ERB4001GT973635.
References
André, R., D. Grésillon, C. Hanuise, and J.-P. Villain,
Auroral ionosphere
plasma turbulence transport coefficient: Direct observations from radar
coherent backscattering, in
1998 International Congress on Plasma Physics,
edited by P. Pavlo, vol. 22C, pp. 1126-1129, ECA, European Physical Society,
1998.
André, R., M. Pinnock, and A. S. Rodger,
On the SuperDARN autocorrelation
function observed in the cusp,
Geophys. Res. Lett., 26, 3353,
1999.
Baker, K. B., R. A. Greenwald, J. M. Ruohoniemi, J. R. Dudeney, M. Pinnock,
P. T. Newell, M. E. Greenspan, and C.-I. Meng, Simultaneous HF radar and
DMSP observations of the cusp,
Geophys. Res. Lett., 17, 1869,
1990.
Baker, K. B., J. R. Dudeney, R. A. Greenwald, M. Pinnock, P. T. Newell,
A. S. Rodger, N. Mattin, and C.-I. Meng, HF radar signatures of the
cusp and low-latitude boundary layer,
J. Geophys. Res., 100, 7671,
1995.
Baker, K. B., A. S. Rodger, and G. Lu, HF radar observations of the dayside
magnetic merging rate: A Geospace Environment Modeling boundary layer
campaign study,
J. Geophys. Res., 102, 9603,
1997.
Barthes, L., R. André, J.-C. Cerisier,
and J.-P. Villain,
Separation of multiple echoes using a high resolution
spectral analysis in SuperDARN HF radars,
Radio Sci., 33, 1005,
1998.
Borovsky, J. E., Auroral arcs thicknesses as predicted by various theories,
J. Geophys. Res., 99, 6101,
1993.
Cabrit, B., Diffusion collective de la
lumiere par un gaz turbulent,
Ph.D. thesis,
Universite de Paris 6, Paris, 1992.
Cowley, S. W. H., and M. Lockwood,
Excitation and decay of solar wind-driven
flows in the magnetosphere-ionosphere system,
Ann. Geophys., 10, 103,
1992.
Dudeney, J. R., A. S. Rodger, M. P. Freeman, J. Pickett, J. Scudder,
G. Sofko, and M. Lester, The nightside ionospheric response to IMF
By changes,
Geophys. Res. Lett., 25, 2601,
1998.
Dyrud, L. P., M. J. Engebretson, J. L. Posh, W. J. Hughes,
H. Fukunishi, R. L. Arnoldy, P. T. Newell, and R. B. Horne,
Ground observations and possible source regions of two types
of Pc1-2 micropulsation at very high-latitudes,
J. Geophys. Res., 102, 27,011,
1997.
Erlandson, R. E., and B. J. Anderson, Pc1
waves in the ionosphere: A statistical
study,
J. Geophys. Res., 101, 7843,
1996.
Gary, J. B., L. J. Zanetti, B. J. Anderson, T. A. Potemra,
J. H. Clemmons, J. D. Winningham, and
J. R. Sharber, Identification of auroral oval
boundaries from in situ magnetic field measurements,
J. Geophys. Res., 103, 4187,
1998.
Greenwald, R. A., K. B. Baker, R. A. Hutchins,
and C. Hanuise, An HF phased array radar
for studying small-scale structure in the
high-latitude ionosphere,
Radio Sci., 20, 63,
1985.
Grésillon, D., B. Cabrit, J.-P. Villain,
C. Hanuise,
A. Truc, C. Laviron, P. Hennequin, F. Gervais,
A. Quemeneur, X. Garbet, J. Payan, and P. Devynck,
Collective scattering of electromagnetic waves
and cross-B plasma diffusion,
Plasm. Phys. Contr. Fus., 34, 1985,
1992.
Gurnett, D. A., Auroral plasma waves, in
Auroral Physics,
edited by C.-I. Meng, M. J. Rycroft, and L. A. Franck,
chap. IV-6, pp. 241-254, Cambridge University Press, 1991.
Hanuise, C., J.-P. Villain, D. Grésillon,
B. Cabrit, R. A. Greenwald,
and
K. B. Baker, Interpretation of hf radar doppler spectra by collective wave
scattering theory,
Ann. Geophys., 11, 29,
1993.
Heppner, J. P., and N. C. Maynard, Empirical high-latitude electric field
models,
J. Geophys. Res., 92, 4467,
1987.
Kintner, P. M., Observations of velocity shear driven plasma turbulence,
J. Geophys. Res., 81, 5114,
1976.
Lewis, R. V., M. P. Freeman, A. S. Rodger, G. D. Reeves, and
D. K. Milling, The
electric field response to the growth phase and expansion phase onset of a
small isolated substorm,
Ann. Geophys., 15, 289,
1997.
Matsuoka, A., K. Tsuruda, H. Hayakawa, T. Mukai, A. Nishida, T. Okada,
N. Kaya, and H. Fukunishi, Electric field fluctuations and charged
particle precipitation in the cusp,
J. Geophys. Res., 98, 11,225,
1993.
Maynard, N. C., T. L. Aggson, E. M. Basinka, W. J. Burke, P. Craven,
W. K. Peterson, M. Sugiura, and D. R. Weimer, Magnetospheric boundary
dynamics: DE 1 and DE 2 observations near the magnetopause and cusp,
J. Geophys. Res., 96, 3505,
1991.
Ossakow, S. L., and P. K. Chaturvedi, Current convective instability
in the diffuse aurora,
Geophys. Res. Lett., 6, 332,
1979.
Pinnock, M., A. S. Rodger, J. R. Dudeney, F. Rich, and K. Baker,
High-spatial and temporal observations of the ionospheric cusp,
Ann. Geophys., 13, 919,
1995.
Pinnock, M., A. S. Rodger, K. B. Baker, G. Lu, and M. Hairston,
Conjugate observations of the day-side reconnection electric
field: A GEM boundary layer campaign,
Ann. Geophys., 17, 443,
1999.
Pudovkin, M. I., A. Steen, and U. Brandstrom, Vorticity in the magnetospheric
plasma and its signatures in the aurora dynamics,
Space Sci. Rev., 80, 411,
1997.
Rich, F. J., and N. C. Maynard,
Consequences of using simple analytical functions for
the high-latitude convection electric field,
J. Geophys. Res., 94, 3687,
1989.
Rodger, A. S., S. B. Mende, T. J. Rosenberg, and K. B. Baker,
Simultaneous optical and HF radar observations of the
ionospheric cusp,
Geophys. Res. Lett., 22, 2045,
1995.
Schiffler, A., G. Sofko, P. T. Newell, and R. A. Greenwald, Mapping the outer
LLBL with SuperDARN double-peaked spectra,
Geophys. Res. Lett., 24, 3149,
1997.
Villain, J.-P., R. A. Greenwald, K. B. Baker, and J. M. Ruohoniemi,
HF radar observations of
E region plasma irregularities produced
by oblique electron
streaming,
J. Geophys. Res., 92, 12,327,
1987.
Villain, J.-P., R. André, C. Hanuise,
and D. Grésillon, Observation
of the high latitude ionosphere by HF radars: Interpretation in
terms of collective wave scattering and characterization of turbulence,
J. Atmos. Terr. Phys., 58, 943,
1996.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.2.0) on August 4, 2000.
 Figure 1 shows the average spectral width observed in the low-altitude
ionosphere by HF radars in the northern hemisphere. Its main characteristic
is that the spectral width is low at low latitudes and inside the polar cap
(
Figure 1 shows the average spectral width observed in the low-altitude
ionosphere by HF radars in the northern hemisphere. Its main characteristic
is that the spectral width is low at low latitudes and inside the polar cap
( 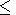 150 m s
-1 ), but increases up to 200 m s
-1 in the auroral
oval, and is at a maximum inside the cusp
( > 250 m s
-1 ). These results
have been determined before
(J. P. Villain and R. A. Greenwald, unpublished data, 1994)
using a similar statistical database. A more
detailed presentation of these two statistical studies
is the subject of a forthcoming paper
[Villain et al., manuscript in preparation, 1999].
Here, the physical mechanisms that lead to these high-spectral
widths are reviewed and discussed.
150 m s
-1 ), but increases up to 200 m s
-1 in the auroral
oval, and is at a maximum inside the cusp
( > 250 m s
-1 ). These results
have been determined before
(J. P. Villain and R. A. Greenwald, unpublished data, 1994)
using a similar statistical database. A more
detailed presentation of these two statistical studies
is the subject of a forthcoming paper
[Villain et al., manuscript in preparation, 1999].
Here, the physical mechanisms that lead to these high-spectral
widths are reviewed and discussed.
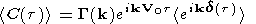
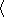 kd(t)
kd(t) 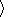 . The
average expressed by the brackets is taken over the
whole range gate and integration time (typically 7 s).
In equation (1), the second term refers to large-scale
processes (greater than a range-beam cell) and the third
one to micro-scale processes (size of the irregularities).
. The
average expressed by the brackets is taken over the
whole range gate and integration time (typically 7 s).
In equation (1), the second term refers to large-scale
processes (greater than a range-beam cell) and the third
one to micro-scale processes (size of the irregularities).



 v ), the results presented
in
v ), the results presented
in  100 km), specific
events in the solar wind-magnetosphere-ionosphere
system can induce smaller-scale perturbations in
the ionospheric convection, such as flux transfer events or
travelling convection vortices. To clearly evaluate their
effects on the ACF, we have conducted a realistic simulation
of the radar processing technique. We first apply the simulation to a
velocity shear that could be induced by either a large-scale
convection reversal, as shown previously, or by an auroral arc.
Secondly, the simulation is applied to meso-scale vortices (
100 km), specific
events in the solar wind-magnetosphere-ionosphere
system can induce smaller-scale perturbations in
the ionospheric convection, such as flux transfer events or
travelling convection vortices. To clearly evaluate their
effects on the ACF, we have conducted a realistic simulation
of the radar processing technique. We first apply the simulation to a
velocity shear that could be induced by either a large-scale
convection reversal, as shown previously, or by an auroral arc.
Secondly, the simulation is applied to meso-scale vortices (