Foreshock effects on near-Earth interplanetary magnetic field correlations

Z. Kaymaz

Istanbul Technical University, Istanbul, Turkey

D. Sibeck

Applied Physics Laboratory, Johns Hopkins University, Laurel, Maryland

Contents

Abstract

1. Introduction

Previous studies show that solar wind monitors located far upstream (e.g., at 200  R_E ) often fail to predict the IMF near Earth. Russell et al. [1980] compared ISEE 1 and ISEE 3 observations. They noted that the IMF exhibits considerable variability even on very short time scales (e.g., ~10 minutes) and concluded that ISEE 3 is not a very good solar wind monitor for geomagnetic studies requiring accurate timing. Only 25% of the correlation coefficients exceeded 0.85 and another 25% were less than 0.5. Crooker et al. [1982] presented the results of a statistical study employing 800 hours of simultaneous ISEE 3 and ISEE 1 and 2 IMF observations in 1978 and 1979. Their analysis showed that the correlation coefficients exceeded 0.8 only for some 25% of the time, increased with the decreasing distance between the two spacecraft in the plane perpendicular to the Earth-Sun line, and increased with increasing IMF variance. They were unable to reproduce the result obtained by Chang and Nishida [1973], namely that higher correlations are associated with increasing solar wind speeds. Correlations also appear to be greater along rather than perpendicular to IMF field lines [Collier et al., 1998; Crooker et al., 1982].

Accuracy in determining the arrival times for solar wind features impinging on the magnetopause is crucial for many magnetospheric and ionospheric studies, in particular for determining whether or not solar wind features trigger substorm onsets. However, even when similar features are observed both far upstream and just outside the Earth's bow shock, uncertainties in predicting the arrival times remain large. While Kelly et al. [1986] showed that taking the IMF orientation into consideration helps determine arrival times, Collier et al. [1998] have shown that errors in arrival time estimates increase as the monitoring spacecraft moves upstream or off the Earth-Sun line.

In this paper, we consider possible factors controlling the degree of correlation between near-Earth interplanetary magnetic fields observed by ISEE 1 and IMP 8. Even though both Russell et al. [1980] and Crooker et al. [1982] noted the possible influence of upstream waves upon the correlation coefficients, neither quantified their effect. Here, we show that the foreshock waves produced significantly reduce correlations in the vicinity of Earth. Our results imply that some of the poor correlations obtained in earlier studies that made use of spacecraft near Earth also resulted from the foreshock effects. Since many magnetospheric phenomena require the use of a solar wind monitor, our results emphasize the need for caution in choosing both monitors far upstream and just outside the bow shock.

2. Data Sets and Results

We present preliminary results from a statistical study correlating IMP 8 and ISEE 1 interplanetary magnetic field observations (IMF) from 1978 to 1981, including the time interval originally selected by Crooker et al. [1982]. IMP 8's orbit is nearly circular in the xy plane with an apogee of 35  R_E. It enters the solar wind on each orbit. By contrast, ISEE 1 has an elliptical orbit with an apogee of 23  R_E and only encounters the solar wind half the year. Here, we use 4s ISEE 1 and 15.36s IMP 8 IMF data averaged/interpolated to 15 seconds. We identified 268 intervals each of 2-hour duration when both spacecraft were in the solar wind. Using standard correlation methods, we computed the correlation coefficients for each component and the magnitude of the field for a wide range of lag times during each interval. We also calculated the hybrid correlation coefficient ( r_hyb=(r_x² + r_y² + r_z² +r²_Bmag)/4 )^1/2 used by Crooker et al. [1982] to identify the best lag time for all the components. Finally, we computed the average peak correlation coefficients by averaging the maximum correlation coefficients for each individual component and the magnitude [e.g., Collier et al., 1998].

Figure 1 presents histograms of the peak correlation coefficients for each magnetic field component, the magnitude of the field, the peak hybrid ( r_hyb ), and the average correlation (rave) coefficients in our study. Table 1 compares our hybrid correlation coefficients with those obtained by Crooker et al. [1982] and Collier et al. [1998]. The table includes the average correlation coefficient and the correlation coefficient for the magnetic field magnitude. Figure 1 and the table show that only about 12% of the correlation coefficients that we obtained exceeded 0.8, a percentage significantly lower than those obtained by either Crooker et al. [1982] or Collier et al. [1998] despite the fact the spacecraft we use were situated much closer to each other than those in the previous studies. Figure 2 shows how the correlation coefficients vary with the distance between IMP 8 and ISEE 1 in the yz plane. The light solid line in each panel gives the least square fit to the data. As in previous studies, the correlation coefficients decrease slightly with increasing separation. However, Figure 2 clearly reveals that we often obtain poor correlations even when the spacecraft separation is very small.

Inspection of case studies can help demonstrate why this is the case. Figure 3 shows examples typifying two categories of IMP 8 and ISEE 1 near-Earth IMF observations. The two panels present total magnetic field strength observations by ISEE 1 (top curve) and IMP 8 (bottom curve) on August 21, 1979 (top panel) and October 7, 1979 (bottom panel). Large spikes flag missing data intervals. In the upper example, both spacecraft observed large amplitude high frequency waves. As a result, the correlation coefficient was only 0.27. By contrast, neither spacecraft observed such waves in the second example and all the features seen could be matched for a time lag near 6 minutes. The correlation coefficient for this case was 0.85. Figure 4 presents corresponding spacecraft trajectories and nominal bow shock/magnetopause positions in the x - R plane. Enhanced solar wind dynamic pressures moved the latter boundaries earthward of the nominal positions, thereby enabling both spacecraft to remain within the solar wind during the intervals studies.

By identifying intervals when either high frequency magnetic field fluctuations or energetic ion fluxes were observed at either spacecraft, we separated the 268 two-hour intervals into foreshock and non-foreshock categories. Of the 268 cases, foreshock waves were present in 141 cases (52%) but absent in the remaining 125 cases. Figures 5a and 5b show correlation coefficients for the foreshock and non-foreshock cases separately. Figure 5 clearly illustrates the fact that foreshock waves greatly diminish magnetic field correlations. Since all previous IMF correlation studies have employed spacecraft which were frequently within the foreshock, it seems very likely that many of their poor correlation cases also resulted from the presence of foreshock-generated high frequency waves.

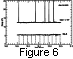Even when neither spacecraft lies within the foreshock (as indicated by the presence of high frequency waves), correlation coefficients can be poor. About 30% of the non-foreshock coefficients shown in Figure 5b are less than 0.5. A reexamination of all of these intervals indicates that the 25% of low correlation coefficients in these cases results from nearly constant magnetic field strengths and orientations at both spacecraft. Figure 6 presents an example of one of these cases in a format similar to that of Figures 3. The average and the standard deviation of the field for ISEE 1 are 5.6 nT and 0.09 nT, and for IMP 8 are 5.5 nT and 0.15 nT. The field strength shows no significant variation at either spacecraft for this interval and the correlation coefficient is therefore low, 0.27. However, the fact that the correlation coefficient is low does not mean that the mean value of the field strength or its components cannot be predicted. For space weather purposes, either monitor could serve as an adequate solar wind monitor.

3. Summary and Conclusions

In this study, we presented initial results from a statistical analysis of 268 two-hour intervals of simultaneous ISEE 1 and IMP 8 IMF observations. We demonstrated that the high-frequency waves generated in the foreshock are a major cause of poor correlation between the observations made by the two spacecraft and suggested that they are also a major cause for poor correlations obtained in previous studies which compared IMF observations from the L1 point with those immediately upstream from Earth. We noted that 30% of the low correlations in the non-foreshock cases occurred during intervals of stable IMF orientation and strength. While the correlation coefficients are low during these intervals, our ability to predict the solar wind input into the magnetosphere remains high.

Acknowledgments

References

Chang, S. C., and A. Nishida, Spatial Structure of Transverse Oscillations in the Interplanetary Magnetic Field, Astrophys. and Space Sci., 23, 301 1973.

Collier, M. R., J. A. Slavin, R. P. Lepping, A. Szabo, and K. Ogilvie, Timing accuracy for simple planar propagation of magnetic field structures in the solar wind, Geophys. Res. Lett., 25, 2509, 1998.

Crooker, N. U., G. L. Siscoe, C. T. Russell, and E. J. Smith, Factors controlling degree of correlation between ISEE 1 and ISEE 3 interplanetary magnetic field measurements, J. Geophys. Res., 87, 2224, 1982.

Kelly, T. J., N. U. Crooker, G. L. Siscoe, C. T. Russell, and E. J. Smith, On the use of a sunward libration-point-orbiting spacecraft as an interplanetary field monitor for magnetospheric studies, J. Geophys. Res., 91, 5629, 1986.

Russell, C. T., G. L. Siscoe, and E. J. Smith, Comparison of ISEE 1 and 3 interplanetary magnetic field observations, Geophys. Res. Lett., 7, 381, 1980.