International Journal of Geomagnetism and Aeronomy
Vol 2, No. 1, June 2000
IMF length scales and predictability: The two length scale medium
Michael R. Collier, Adam Szabo, James A. Slavin, and R. P. Lepping
NASA/Goddard Space Flight Center, Laboratory for Extraterrestrial
Physics, Greenbelt, Maryland
S. Kokubun
Solar-Terrestrial Environment Laboratory, Nagoya University,
Toyokawa, Japan
Contents
Abstract
We present preliminary results from a systematic study
using simultaneous data from three spacecraft, Wind, IMP 8
and Geotail to examine interplanetary length scales and their implications
on predictability for magnetic field parcels in the typical solar wind.
Time periods were selected when all three spacecraft were within one
Earth radius of residing in a plane that includes the GSE
x direction so
that if the parcel fronts were strictly planar
at some angle relative to the Sun-Earth line and radially convecting, the
two adjacent spacecraft pairs would determine the same phase front angles.
After correcting for the motion of the Earth relative to the interplanetary
medium and deviations in the solar wind flow from radial, we used
differences in the measured front angle between the
two spacecraft pairs to determine structure radius of curvature.
Results indicate that the typical radius of curvature for these IMF
parcels is of the order of 100
RE. This implies that there
are two important IMF scale lengths relevant to predictability:
(1) the well-established scale length over which correlations observed by
two spacecraft decay along a given IMF parcel, of the order of a few tens
of Earth radii and
(2) the scale length over which two spacecraft are
unlikely to even observe the same parcel
because of its curvature, of the order of a hundred Earth radii.
Introduction
Studies concentrating on solar wind-magnetosphere interaction frequently
and routinely use upstream monitors to determine how changes in solar wind
properties affect the magnetosphere. Not uncommonly, the only remark made
is that an "upstream monitor" was employed as if location upstream were
completely irrelevant.
There appears to be a lack of appreciation of the interplanetary medium as
a structured, as opposed to homogeneous, entity.
Yet Sun-Earth connection studies which aim to determine how accurately an
upstream monitor can predict the solar wind parameters that actually
interact with the magnetosphere (or even reach the outer heliosphere
[Sibeck and Richardson, 1997])
are showing that the interplanetary medium
is not uniform over magnetospheric scale lengths.
Because the scale length of the geoeffective flow is only a few Earth radii
around the Sun-Earth line
[Burke et al., 1999],
the trick to
predicting geoeffectiveness is to determine what observations at the
upstream spacecraft location reveal about conditions within a couple Earth
radii of the Sun-Earth line,
and this may be inferred by using observations from multiple spacecraft.
It should be pointed out that these types of studies have importance beyond
solar wind-magnetosphere interactions. They apply, for example, to bow
shock modeling
[Safránková et al., 1999].
Even
interplanetary multi-spacecraft studies using one spacecraft for
"baseline" solar wind must have an appreciation for scale lengths and
coherency within the interplanetary medium to evaluate baseline accuracy
[Owen et al., 1996].
2. Comments on the Two Spacecraft Study of
Collier et al. [1998]
This paper elaborates and extends the two spacecraft work described in
Collier et al. [1998]
which employed Wind and IMP 8 magnetic field
data. In their correlation study, they restricted attention to those cases
exhibiting good correlation, which was defined as cases having a peak
Crooker hybrid correlation coefficient above 0.8
[Crooker et al., 1982].
This was done because most cases had peak correlation coefficients
in the range 0.5-0.8 so that, for example, evaluating an average peak
Crooker hybrid correlation coefficient would show little effect and have
large dispersions.

 Nevertheless, we can learn something by examining all cases
together.
Figure 1
shows for all of the two hour data intervals studied in
Collier et al. [1998],
the angular distribution
of the magnetic field direction and how the average peak Crooker hybrid
correlation varies with the average magnetic field direction
projected into the ecliptic plane. The solid data points and line show the
average correlation for all 543 cases (not just the good correlation cases)
falling within that
10o bin.
The minimum average peak Crooker
hybrid correlation coefficient in a
10o bin is 0.519 and the
maximum is 0.710, so that the difference between the minimum and maximum
average peak Crooker hybrid correlation coefficient in a
10o bin
is only 0.191, close to the typical scatter in the data ( 1s ),
indicated by the error bars, so some might argue this effect is not
convincing.
(However, Figure 2
which will be discussed in detail below shows that most
cases of good correlation are around
90o as compared to those at
the Parker spiral direction.)
Nevertheless, we can learn something by examining all cases
together.
Figure 1
shows for all of the two hour data intervals studied in
Collier et al. [1998],
the angular distribution
of the magnetic field direction and how the average peak Crooker hybrid
correlation varies with the average magnetic field direction
projected into the ecliptic plane. The solid data points and line show the
average correlation for all 543 cases (not just the good correlation cases)
falling within that
10o bin.
The minimum average peak Crooker
hybrid correlation coefficient in a
10o bin is 0.519 and the
maximum is 0.710, so that the difference between the minimum and maximum
average peak Crooker hybrid correlation coefficient in a
10o bin
is only 0.191, close to the typical scatter in the data ( 1s ),
indicated by the error bars, so some might argue this effect is not
convincing.
(However, Figure 2
which will be discussed in detail below shows that most
cases of good correlation are around
90o as compared to those at
the Parker spiral direction.)
Thus there is a clear tendency for higher correlation
to be observed when the IMF is perpendicular to the Sun-Earth line,
consistent with the findings of
Crooker et al. [1982]
who deduced
that magnetic features are correlated a longer distance along the field
than perpendicular to the field.
This implies better correlation when the field is
perpendicular to the Sun-Earth line because in this case the same field
line will
intersect both spacecraft but at different locations along the field
line. When the field line is parallel or anti-parallel to the
Sun-Earth line, the two spacecraft sit on different field lines
and are separated solely perpendicular to the field resulting in lower
correlation.
However, as discussed above, the effect is not that large.
This may provide an explanation for why studies have typically found that
the optimal assumed angle for propagation is neither perpendicular to the
Sun-Earth line nor along the Parker spiral, but rather between the two.
For example,
Richardson and Paularena [1998]
found ~
115o for
plasma structures
[see also
Paularena et al., 1998;
Richardson et al., 1998].
They interpret these results as indicating that time-dependent changes in
the solar wind source are as important as longitudinal variations of the
source. Here we provide an alternative explanation.
The dashed lines in both Figure 1 and 2 show the probability distribution
for
the IMF direction, which is, of course, peaked along the Parker spiral
direction,
135o, with a minimum, although non-negligible,
probability of having a two-hour averaged field direction in the
ortho-Parker direction,
45o.
Non-standard field directions are attributed to large amplitude waves,
discontinuities, convected structures and variations in flow speed but in
some cases could indicate the presence of unusual field configurations
at
the solar wind source, at a few solar radii, where it has been usually
assumed that field lines are near radial
[Jones et al., 1998].
The angular distribution of good correlation cases, those cases which can
be reliably employed to establish timing, will depend on two
factors:
(i) the distribution of the average correlation coefficients
(the solid line in Figure 1) because, all things being equal, good
correlation cases will most likely occur at the angle where the average
correlation coefficient is maximum,
90o, and (ii) the
distribution of field angles (the dashed line in Figure 1)
because, again all
things being equal, the more cases with the IMF at a given angle (e.g.
135o, the Parker spiral direction), the more likely a good
correlation case will occur at that angle. Consequently, we expect the
distribution of good correlation cases to peak somewhere between
90o and 135o, a compromise between the two distributions.
Indeed, Figure 2 shows with the solid line the direction
probability
distribution for the 67 cases with good correlation, an average peak
Crooker hybrid correlation coefficient above 0.80. Here, the bins are
30o wide and the average is 106.3o, as expected, a
compromise between perpendicular to the Sun-Earth line and the Parker
spiral direction.
This may also explain, when the large width of the distribution is also
considered, why neither convection nor corotation shifting appears to be
superior for timing purposes
[Couzens and King, 1986;
Kelly et al., 1986;
King, 1986].
3. Possible GSE x-Dependence
 In agreement with the conclusions of
Lyons et al. [1997]
and of
Silverman et al. [1997]
for SOHO/Wind plasma data correlations,
we do not find any convincing evidence of an effect due to spacecraft
separation in the GSE
x -direction (parallel to the solar wind flow
direction) in the correlation results. In an attempt to isolate the effects
of parallel spacecraft separation from perpendicular spacecraft separation,
we examined those cases of the 543 Wind/IMP 8 two hour data intervals in
which the spacecraft were separated by 50-60 Earth radii perpendicular to
the Sun-Earth line. This interval was picked to maximize the parallel range
and the case statistics. Figure 3 shows the average Crooker hybrid
correlation coefficient as a function of spacecraft separation in the GSE
x -direction for a fixed perpendicular separation of 50-60 Earth radii.
Although the
x -separation spans nearly a factor of two, from 140 to
260
RE, there is no apparent change in the
average correlation coefficient.
In agreement with the conclusions of
Lyons et al. [1997]
and of
Silverman et al. [1997]
for SOHO/Wind plasma data correlations,
we do not find any convincing evidence of an effect due to spacecraft
separation in the GSE
x -direction (parallel to the solar wind flow
direction) in the correlation results. In an attempt to isolate the effects
of parallel spacecraft separation from perpendicular spacecraft separation,
we examined those cases of the 543 Wind/IMP 8 two hour data intervals in
which the spacecraft were separated by 50-60 Earth radii perpendicular to
the Sun-Earth line. This interval was picked to maximize the parallel range
and the case statistics. Figure 3 shows the average Crooker hybrid
correlation coefficient as a function of spacecraft separation in the GSE
x -direction for a fixed perpendicular separation of 50-60 Earth radii.
Although the
x -separation spans nearly a factor of two, from 140 to
260
RE, there is no apparent change in the
average correlation coefficient.
4. A Simple Timing Model
If we assume the distribution of parcel front angles (see
[Collier et al., 1998, Figure 3])
is wide enough to be approximated by a uniform
distribution, we can find an analytic expression for the distribution of
lag times. Note that by parcel front, we mean the direction along which the
correlation between the magnetic field observed at two different points is
greatest. Parcel fronts are lines of maximum correlation.
If their angular distribution is uniform, then the probability of a given
phase front being at a particular angle is simply
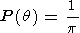 | (1) |
Simple trigonometry shows that if the spacecraft are separated
by distances
dpar and
dper parallel
and perpendicular to the Sun-Earth line, respectively, then
 | (2) |
where
vsw is the solar wind speed.
Given that
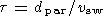 | (3) |
this can be re-written as
 | (4) |
where
Dt is the difference
between the observed and the
convection lag times. Thus, we can write an expression for
q :
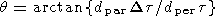 | (5) |
To determine what this says about the distribution of lag times,
we use the expression
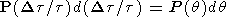 | (6) |
which means simply that, using
P(q) from (1) above,
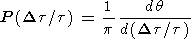 | (7) |
Evaluating this expression using (5) above results in
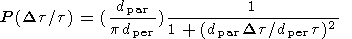 | (8) |
which is a Cauchy distribution. Note that this distribution has no mean or
standard deviation (the integrals diverge) resulting in some
counter-intuitive properties.
5. Comment on Cauchy Flight Model
One example is that an attempt to determine an average
Dt/t
from a distribution of this type results in a Lévy
flight process and,
more specifically, a Cauchy flight
[Collier, 1993a, 1993b]
due to the
power law nature of the tail.
Whereas normally
s/N where
s is the standard deviation
and
N is the number of events decreases as
1/N1/2, for a Cauchy
flight process,
s/N does not decrease with
N (i.e.
s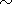 N ).
Thus, increasing the number of measurements will not increase the accuracy of the
measurement. Fundamentally, this is due to the high
probability of very bad timing errors resulting from the tails "throwing
off" the averaging process. However, it raises the intriguing possibility
that the accuracy in determining convection times using two upstream
observations will not improve with multiple measurements - that is there
will be the same uncertainty whether one or a thousand measurements are
made
[Schroeder, 1991].
N ).
Thus, increasing the number of measurements will not increase the accuracy of the
measurement. Fundamentally, this is due to the high
probability of very bad timing errors resulting from the tails "throwing
off" the averaging process. However, it raises the intriguing possibility
that the accuracy in determining convection times using two upstream
observations will not improve with multiple measurements - that is there
will be the same uncertainty whether one or a thousand measurements are
made
[Schroeder, 1991].
6. Short Scale Length (~10s of RE)
It has become well-established that the scale length over
which correlation
decays along a solar wind parcel is of the order many tens of Earth
radii. Table 1
lists six studies, all of which applied different
techniques, which support a scale length of many tens of Earth radii,
particular values ranging from ~10 to 60, depending on the details of
the study.
Crooker et al. [1982]
using ISEE 1 and ISEE 3 data showed that during
periods of low IMF variance good correlations tend to occur when the
distance between the two spacecraft perpendicular to the IMF is less than
20
RE. However, during periods of high variance the scale size
is larger, about 50
RE.
Borodkova et al. [1995]
employed
Prognoz 10 as a solar wind monitor for periods when transient variations in
the dayside magnetospheric magnetic field were observed by GOES 5 and 6
geosynchronous satellites. They found a decrease in the success rate for
associating the transient events with solar wind features as Prognoz 10
moved farther off the Sun-Earth line. The decrease has a scale length of
the order of a few tens of Earth radii based on their Table 2.
Lyons et al. [1997]
used Wind, IMP 8 and Geotail data along with
CANOPUS meridian-scanning photometer data to investigate the IMF behavior
relating to substorm onsets. They found that a clear IMF trigger, a
northward turning or a reduction in the magnitude of the
y component, could
be identified in 14 of the 20 substorms considered and the probability of
trigger identification is a strong function of IMF monitor distance from
the Sun-Earth line: 89% for monitors that are within 30
RE of
the Sun-Earth line but only 50% for monitors located 30-56.7
RE from the Sun-Earth line.
Sotirelis et al. [1997]
used polar rain observations from DMSP
along with IMF observations from IMP 8 to show that a solar wind monitor
greater than 10
RE from the Sun-Earth line has a 20% chance of
seeing a significantly different IMF than that impinging on the
magnetosphere.
Collier et al. [1998]
using IMF data from Wind and IMP 8 showed
that the probability of obtaining a good correlation between observations
made off the Sun-Earth line and those along the Sun-Earth line is an
exponential-like function of the monitor distance from the Sun-Earth line
with an
e -folding distance of about 40
RE.
Finally,
Kessel et al. [1999]
used Geotail, Wind and IMP 8 data to
examine a two hour time period on September 14, 1995 when Geotail on the
dawnside measured magnetic field directions 60-120 degrees different from
those measured by Wind on the duskside ( y -GSE separation of 60
RE ).
Kessel et al.
suggest there is a kink in the magnetic field
near the Sun-Earth line and, insofar as the inference is geometrical, this
study may be more pertinent to the longer, curvature, scale length to be
discussed next, although in size it appears to fall into the short scale
length category.
The sum total of these studies indicates that the IMF has one (short) scale
length of the order of many tens of Earth radii (although the
Kessel et al. [1999]
study may be more pertinent to the longer scale length to
be discussed in the next section).
7. Long Scale Length (~100 RE)
It is the contention of this paper that in addition to the short scale
length of the order of many 10s of
RE representing
correlation decay along a parcel there is a longer scale length of the
order of 100
RE representing large scale geometry.
 Previous work by
Crooker et al. [1982]
using ISEE 1 and ISEE 3 data
hinted at the presence of this longer scale length. The solid circular data
points, corresponding to the left hand
y axis, on Figure 4 show a
replotting of the data shown in the two panels of Figure 2 of
Crooker et al. [1982].
The ratio of the number of cases with poor correlation (less
than 0.5) to the number of cases with good correlation (greater than 0.8)
increases abruptly at around 100 Earth radii. We have verified the
Crooker et al.
results with a similar approach using Wind and IMP 8 data as shown
with the square data points and right hand
y axis in Figure 4.
Note that the left and right
y axis scales are different because we are
emphasizing the similar qualitative behavior in the two studies.
Although we see fewer good cases, perhaps because of solar cycle effects,
the same jump observed by
Crooker et al. at around 100
RE is
apparent in our data as well.
Previous work by
Crooker et al. [1982]
using ISEE 1 and ISEE 3 data
hinted at the presence of this longer scale length. The solid circular data
points, corresponding to the left hand
y axis, on Figure 4 show a
replotting of the data shown in the two panels of Figure 2 of
Crooker et al. [1982].
The ratio of the number of cases with poor correlation (less
than 0.5) to the number of cases with good correlation (greater than 0.8)
increases abruptly at around 100 Earth radii. We have verified the
Crooker et al.
results with a similar approach using Wind and IMP 8 data as shown
with the square data points and right hand
y axis in Figure 4.
Note that the left and right
y axis scales are different because we are
emphasizing the similar qualitative behavior in the two studies.
Although we see fewer good cases, perhaps because of solar cycle effects,
the same jump observed by
Crooker et al. at around 100
RE is
apparent in our data as well.
One possible physical interpretation of
these data, corroborated by the
work reported here, is that interplanetary parcels have a characteristic
radius of curvature of about 100
RE, and beyond this
perpendicular spacecraft separation,
the two spacecraft will frequently not
even observe the same field parcel. Hence the dramatic increase in poor
correlation cases which indicates little or no similarity in the
observations at the two spacecraft. This should be contrasted with the
shorter scale length which represents a decay in the probability of a good
correlation and is interpreted as a coherency scale length along a single
parcel.
8. General Comments
Much of the analysis performed examining interplanetary parcels has assumed
planar structure fronts, and one purpose of this study is to determine how
reasonable this assumption is, that is, what is the characteristic radius
of curvature.
However, one difficulty is that, if the structures are perfectly planar,
the orientation is determined by two angles, for example azimuth and
elevation, and two arbitrarily placed spacecraft will only determine one
angle, leaving the other undetermined. To check
this determined angle for consistency with another spacecraft and
infer a radius of curvature, the second spacecraft pair must be placed
geometrically so that the measured angle is the same angle.
A little reflection makes it clear that this means the plane formed by the
three spacecraft must include the solar wind flow direction, assumed for
this purpose to be the GSE
x direction.
In principal, one could perform studies investigating the radius of
curvature both in and out of the ecliptic plane; one would not
generally expect them to be the same. In practice, determining radii of
curvature out of the ecliptic is complicated for two reasons:
(i) The spacecraft move with the Earth at 17
RE per hour and the
convection times from Wind to IMP 8 and Geotail are frequently of the order
of an hour. Consequently, looking for time periods when the plane formed by
the three spacecraft includes the GSE
x axis must consider and account for
the observed parcel lag times which are not known a priori. This is in
contrast to determining curvature in the ecliptic plane where this effect
only changes the effective perpendicular separation between the spacecraft
but not their immersion in the plane. (ii) The spacecraft are usually close
to the ecliptic plane so it is difficult to get large spacecraft
separations perpendicular to the ecliptic plane. Consequently, the
radius of curvatures determined here are effectively in the
ecliptic plane.
9. Selection Criteria
To be considered a valid case for analysis, a number of conditions had to
be met. First, all three spacecraft had to be within one Earth radii of
residing in a plane (close to the ecliptic) that includes the GSE
x -direction, the solar wind flow direction, and be well-separated in the
GSE
y direction. One Earth radius may reflect the accuracy with which
IMP 8's position is currently known. The times when this first condition
was satisfied were determined using data from the Satellite Situation Center
(http://sscweb.gsfc.nasa.gov/).
These "triplanarity" time periods are determined by assuming the solar
wind flows along the
x axis and are given a 1
RE tolerance. The
error introduced by the 1
RE tolerance depends on structure
angle out of (i.e. perpendicular to) the plane which is assumed not so
steep that this will be a significant source of error.
As mentioned earlier, the triplanarity condition assures that both
spacecraft pairs observe the same angle.
The well-separated condition was imposed to make sure that the angles were
well-determined, which requires a wide perpendicular spacecraft separation
(of course, correlation also gets worse with
increasing perpendicular separation). Quantitatively, we required that each
pair of adjacent spacecraft have a perpendicular separation of at least
five Earth radii.
Second, all three spacecraft had to be in the interplanetary medium.
For Wind, which was usually far upstream, this was not an issue. For IMP 8,
we used the solar
wind speeds from MIT
(ftp://space.mit.edu/pub/plasma/imp/www/imp.html),
which are determined only when the spacecraft is in the interplanetary
medium. To assure that the data had no sheath periods in it, we took care
to make sure no one hour intervals adjacent to the bow shock were used
[D. G. Sibeck, private communication, 1999].
For Geotail, we examined the CPI spectrograms
(http://www-pi.physics.uiowa.edu/www/cpi/)
to assure that Geotail was in the solar wind
[Frank et al., 1994].
Geotail was used to establish the even hour
interval used which has good correlation (e.g. 2000-2100) with the
corresponding data intervals for Wind and IMP 8 shifted according to the
observed lag time.
Third, all three of the two-spacecraft pairs had to have clear peaks in the
average correlation coefficient as a function of lag time to assure the
convection lag times are well-defined.
The average correlation coefficient (average of the three components and
magnitude) is more convenient than the Crooker hybrid and mimics its
behavior closely, particularly near the peaks
[e.g. Collier et al., 1998;
Kaymaz and Sibeck, 1999, 2000].
The resultant lag times were then checked for consistency between the three
spacecraft by requiring that the lag time between upstream spacecraft A and
B plus the lag time between upstream spacecraft B and C equal the lag time
between upstream spacecraft A and C to within 72 seconds (0.02 hours -
reasonable uncertainty due to the one minute averaging time) as it must if
all spacecraft were observing the same parcel. This is a strong check in
part because all three lag times are determined separately.
If the parcel is static and undergoes no temporal evolution, then the sum
of the lag times between the upper and lower spacecraft pairs must equal
the lag time between the two outside spacecraft, regardless of parcel
geometry. Thus, the fact that we were not able to find a case with
well-defined lag times that violates this condition supports the inference
that there is little temporal evolution, i.e. GSE-x dependence, that these
parcels undergo.
The magnetic field data from all potential cases were carefully examined
for possible foreshock and sheath contamination
[Berdichevsky et al., 1999;
Zastenker et al., 1999],
as it has been established that foreshock and sheath effects adversely
affect correlation
[Kaymaz and Sibeck, 1999, 2000].
We assured
that there was no evidence of foreshock contamination by looking for
turbulent signatures in the magnetic field data.
This was, of course, only an issue
for Geotail and IMP 8.
10. Corrections to dper
and dpar
Because it is frequently the case that the observed angles based on two
spacecraft pairs are frequently very close, it is important to correct the
spacecraft distances for two effects: (i) the solar wind flow angle and
(ii) the motion of the Earth around the Sun. Both effects will modify the
effective perpendicular spacecraft separation, and the solar wind flow
angle will modify the effective parallel spacecraft separation.
The solar wind flow direction was determined using Wind SWE (96 second
averages) data averaged over the relevant one hour interval shifted for the
Wind-Geotail lag time to determine an angle
b the solar wind flow forms with the GSE
x axis. The perpendicular and
parallel spacecraft separations
dper and
dpar respectively were then modified by the following expressions:
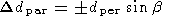 | (9) |
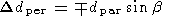 | (10) |
which is simply the small angle approximation of the standard rotation
matrix with the appropriate
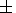 combination selected on the basis of
geometry.
combination selected on the basis of
geometry.
We incorporated the motion of the Earth simply by modifying the
perpendicular spacecraft separation for each pair by an amount dependent on
the observed lag time between the two spacecraft and the speed of the Earth
(30 km s
-1 or about 17
RE /hour) with the sign dependent on the
relative spacecraft locations.
11. Calculating the Curvature of Interplanetary Parcels
Using the observed solar wind lag times between each spacecraft pair,
tobs, the solar wind convection time
t (determined using
Wind SWE data over the appropriate time period inferred by the observed
Wind-Geotail lag time), and the perpendicular and parallel spacecraft
separations,
dpar and
dper respectively, one can
determine the front angle
q using the relationship
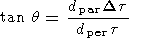 | (11) |
where
Dt = t
- tobs. This is just equation (4).
By obtaining two parcel angles, one for the "lower" (in a GSE
y sense) and
one for the "upper" spacecraft pair ( q1 and
q2 respectively), one may use the expression
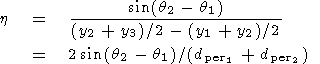 | (12) |
to determine the curvature,
h.
Here
dper1 and
dper2 are the perpendicular separations
of the lower and upper spacecraft pairs, respectively.
The reciprocal of the curvature,
h, yields the radius of curvature
r, which is a more physically intuitive quantity.
We elect, however,
to perform the analysis using
h because frequently the results are
consistent with planar parcels which imply zero curvature but infinite
radius of curvature.
12. Example Cases: August 23, 1995, 2000-2100,
and September 2, 1996, 0200-0300
We have canvassed all of 1996 and about half of 1995 looking
for valid time
periods as described above. So far, we have eight listed in Table 2.
 Figure 5
shows an example of a time period when the plane formed by the
three spacecraft includes the GSE
x axis; Wind, IMP 8 and Geotail are only
a couple of
RE below the ecliptic plane.
As shown in the upper panel, the spacecraft geometry is well-suited for a
determination of structure curvature in that the spacecraft are reasonably
well-separated perpendicular to the Sun-Earth line.
Figure 5
shows an example of a time period when the plane formed by the
three spacecraft includes the GSE
x axis; Wind, IMP 8 and Geotail are only
a couple of
RE below the ecliptic plane.
As shown in the upper panel, the spacecraft geometry is well-suited for a
determination of structure curvature in that the spacecraft are reasonably
well-separated perpendicular to the Sun-Earth line.
Although Geotail is close to the nominal bow shock position, indicated by
the solid line shaped like the bow shock, CPI data from Geotail indicate
that it was in the solar wind at this time.
 Figure 6 shows the cross correlation as a function of lag time
for the
three spacecraft pairs, Geotail/IMP 8, Geotail/Wind and Wind/IMP 8. What
is
plotted here at each lag time is an average correlation coefficient which
represents the average of the correlation coefficients for the magnitude
and the three components of the magnetic field. Note that the lag time from
Wind to IMP 8 (0.15 hours) plus the lag time from IMP 8 to Geotail (0.13
hours) is equal to the lag time from Wind to Geotail (0.27 hours) to within
uncertainty, as it must be if the parcels are coherent and time-stationary.
Figure 6 shows the cross correlation as a function of lag time
for the
three spacecraft pairs, Geotail/IMP 8, Geotail/Wind and Wind/IMP 8. What
is
plotted here at each lag time is an average correlation coefficient which
represents the average of the correlation coefficients for the magnitude
and the three components of the magnetic field. Note that the lag time from
Wind to IMP 8 (0.15 hours) plus the lag time from IMP 8 to Geotail (0.13
hours) is equal to the lag time from Wind to Geotail (0.27 hours) to within
uncertainty, as it must be if the parcels are coherent and time-stationary.
 Figure 7
shows a comparison between magnetic field magnitudes and the GSE
x,
y, and
z components for both Geotail and IMP 8 (left column) and Wind
and IMP 8 (right column). In these figures, the IMP 8 time tags have been
adjusted by the observed lag time to line up the data.
Figure 7
shows a comparison between magnetic field magnitudes and the GSE
x,
y, and
z components for both Geotail and IMP 8 (left column) and Wind
and IMP 8 (right column). In these figures, the IMP 8 time tags have been
adjusted by the observed lag time to line up the data.
One common misconception about correlation studies is that the technique
will focus on one or a few discontinuities in the data set so that, for
example, parcel fronts could be determined by a variance analysis
[Sonnerup and Cahill, 1967].
As is apparent from the figure, this is not the case.
Instead, the technique does seem to try to match the entire field profile
over the time interval without matching up a single feature, an important
point to remember when interpreting these studies:
the parcel front angle does actually represent the entire parcel and not a
particular discontinuity within the parcel.
It is simply the case that the amplitudes of the discontinuities are
usually much too small to dominate the total variance.
Of course, if one focuses specifically on discontinuities, it may
be possible to determine the timing of these particular structures
with greater accuracy
[e.g. Khan and Cowley, 1999].
It is also interesting that one can see clear spatial structure that varies
over the spacecraft perpendicular separation. For example, the spike in the
Geotail
y component at Geotail hour 20.3 is larger at Wind and smaller at
IMP 8, the two spacecraft straddling Geotail
in the
y -GSE direction. Thus, this spike systematically rises in magnitude
from about 1 nT at IMP 8 to about 4 nT at Wind over a perpendicular
distance of twenty or so
RE.
Note from Figure 5
that Geotail is closer in a GSE-
y sense to Wind than to
IMP 8 and the peak average correlation coefficient, as shown in Figure 6, is
the greatest of the three pairs. This is consistent with the correlation
being dependent on perpendicular spacecraft
separation. It should also be pointed out that the Wind-Geotail correlation
is greatest in spite of the largest GSE-
x separation of the three pairs,
also consistent with a smaller or negligible
dependence of correlation on
GSE-
x separation. Finally, the spike at Geotail hour 20.3 is closer in
magnitude to that observed at Wind than that at IMP 8, suggesting not
counter-intuitively that not only
correlation, that is changes, but also the agreement of actual magnetic
field values is dependent on perpendicular spacecraft
separation.
 It is interesting to note that it is not unusual to find time periods when
the spacecraft farther upstream actually observes the parcel later than the
downstream spacecraft due to the orientation of the parcel front. A couple
such time periods occur in the list in Table 2, and the location of the
spacecraft along with the orientation of the parcel front is shown in
Figure 8
for one of these time periods on September 2, 1996, 0200-0300. In
this case,
the straight convection time (which assumes the front lies perpendicular to
the Sun-Earth line) would have IMP 8 observe the parcel 0.035 hours after
Geotail. Instead, IMP 8 observes the parcel 0.02 hours before Geotail
implying a front angle of about 53o, as indicated in Figure 8, and
corroborated by the Wind/Geotail analysis.
It is interesting to note that it is not unusual to find time periods when
the spacecraft farther upstream actually observes the parcel later than the
downstream spacecraft due to the orientation of the parcel front. A couple
such time periods occur in the list in Table 2, and the location of the
spacecraft along with the orientation of the parcel front is shown in
Figure 8
for one of these time periods on September 2, 1996, 0200-0300. In
this case,
the straight convection time (which assumes the front lies perpendicular to
the Sun-Earth line) would have IMP 8 observe the parcel 0.035 hours after
Geotail. Instead, IMP 8 observes the parcel 0.02 hours before Geotail
implying a front angle of about 53o, as indicated in Figure 8, and
corroborated by the Wind/Geotail analysis.
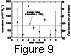 Table 2
column 6 summarizes the curvature results from the eight cases we
have examined so far. Many of the cases are consistent with no curvature,
that is perfectly planar parcels. The curvature for each case is plotted in
Figure 9.
The average curvature is
8.5
Table 2
column 6 summarizes the curvature results from the eight cases we
have examined so far. Many of the cases are consistent with no curvature,
that is perfectly planar parcels. The curvature for each case is plotted in
Figure 9.
The average curvature is
8.5  10-3 RE-1,
implying a typical radius of curvature of 118
RE. Here we quote
unweighted values because weighted values would attach too much importance
to infrequent, well-determined outliers.
10-3 RE-1,
implying a typical radius of curvature of 118
RE. Here we quote
unweighted values because weighted values would attach too much importance
to infrequent, well-determined outliers.
14. Conclusion
 Figure 10 shows the picture of interplanetary parcels that appears
to be
emerging. These parcels are convected approximately with the solar wind
speed with little or no temporal evolution over a couple hundred or less
earth radii. When observing the same parcel two spacecraft have a
correlation scale length of about 30 Earth radii indicated by the gray
scale in Figure 10.
This scale length is not to be confused with the curvature scale length,
and although the scale length is shown the same on all parcels, there is
certainly variability from parcel to parcel.
This means that a spacecraft's ability to determine the characteristics of
the parcel of the interplanetary medium that impacts the magnetosphere will
decay with distance from the Sun-Earth line with a characteristic
e -folding
length of about 30 Earth radii in accordance with this work and the studies
listed in Table 1.
This is the effect illustrated by the gray scale in Figure 10 and is why the
parcels are white in the center and black at the edges.
Figure 10 shows the picture of interplanetary parcels that appears
to be
emerging. These parcels are convected approximately with the solar wind
speed with little or no temporal evolution over a couple hundred or less
earth radii. When observing the same parcel two spacecraft have a
correlation scale length of about 30 Earth radii indicated by the gray
scale in Figure 10.
This scale length is not to be confused with the curvature scale length,
and although the scale length is shown the same on all parcels, there is
certainly variability from parcel to parcel.
This means that a spacecraft's ability to determine the characteristics of
the parcel of the interplanetary medium that impacts the magnetosphere will
decay with distance from the Sun-Earth line with a characteristic
e -folding
length of about 30 Earth radii in accordance with this work and the studies
listed in Table 1.
This is the effect illustrated by the gray scale in Figure 10 and is why the
parcels are white in the center and black at the edges.
However, these parcels also have a radius of curvature of
the order of 100
Earth radii indicated by the curved boundaries of the parcels in Figure 10.
Thus, at a characteristic separation of about a hundred Earth radii, two
spacecraft will frequently not even observe the same field profile, as
evidenced by a dramatic increase in poor correlation cases observed by
Crooker et al. [1982]
and in this study (Figure 3). This means that the
critical question when trying to determine what impacts the Earth based on
observations at distances from the Sun-Earth line of the order of
100
RE is not how well the observations predict what is
happening along the Sun-Earth line, but rather whether there is any
relationship whatsoever between the spacecraft observations and what
impacts the Earth.
Because our observations show that the parcel radius of curvature is
~100
RE which is usually significantly larger than the
typical separation between the spacecraft perpendicular to the Sun-Earth
line, planarity is, in most cases, a reasonable assumption.
In principal, there could be a bias in the results due to radii of
curvature being smaller than the typical interspacecraft separation. This
would bias the results toward larger radii of curvature because shorter
ones would be missed. However, this is probably not a significant effect
because we expect the distribution of radii of curvature to be relatively
well-behaved. Consequently, if we were missing a significant number of
parcels with shorter radii of curvature due to interspacecraft separation
effects, we would expect to observe quite a few cases with radii of
curvature of the order of the perpendicular spacecraft separations. Yet,
the shortest radius of curvature observed is 46
RE with seven of
eight cases greater than 79
RE, and the average is 118
RE.
Thus, it is unlikely that we are missing many parcels with short radii of
curvature.
Correlation studies such as these described herein have a practical aim: to
help us predict space weather. However, because it appears that the basic
morphology of the solar wind is determined very close to the Sun
[Breen et al., 1999],
such studies may illuminate various solar processes.
So, given the existence of a correlation scale length of many 10s of
RE and a geometric scale length of ~100
RE, a
natural question to ask is what processes in the solar corona or
interplanetary medium would produce these scale lengths.
One possibility is that large scale effects are created by very small scale
structures too minute to observe. However, evidence
suggests that it might be possible to associate discrete structures seen in
the solar wind with specific details of the solar atmosphere
[Fisher and Guhathakurta, 1995].
Also,
Roberts and Ghosh [1999]
have raised the interesting possibility that
the parcel phase fronts and curvature may be due to velocity shear in the
solar wind.
Furthermore, the average solar wind speed for the eight cases examined in
this study is 377 km s
-1,
which is lower than the average solar wind speed.
This is consistent with
Chang and Nishida's [1983]
observation that lower
solar wind speeds are associated with higher correlation. However, lower
speed solar wind
tends to be more turbulent, more of a "garbage" wind that is not as
well-behaved as the higher speed solar wind, and it is significant that the
typical radius of curvature is still large, of the order of 100
RE.
A difference in the radius of curvature of solar wind parcels between
slow and fast wind could be linked to the origin of the slow wind on the
solar surface.
Finally, if the 100
RE scale length is extrapolated back
radially (214
R<IMG SRC='latex032.gif' ALT="odot"> )
to the solar surface, one gets a scale length of
about 3000 km. However, it is likely that super-radial expansion occurs, so
that the actual scale length will be slightly smaller
and may be related to the typical distance between granular cells on the
photosphere which is about 1800 km
[Priest, 1997].
Perhaps this
scale length represents the spacecraft sampling parcels from different
granular cells.
Acknowledgments
Special thanks to Kathleen McClernan for helping
with some of the programming used in this study. Also thanks to Dimitris
Vassiliadis for helpful references.
References
Berdichevsky, D., G. Thejappa, R. J. Fitzenreiter,
R. P. Lepping,
T. Yamamoto, S. Kokubun, R. W. McEntire,
D. J. Williams, and R. P. Lin, Widely
spaced wave-particle observations during GEOTAIL and Wind magnetic
conjunctions in the Earth's ion foreshock with near-radial interplanetary
magnetic field,
J. Geophys. Res., 104, 463,
1999.
Borodkova, N. L., et al.,
A case and statistical study of transient magnetic field
events at geosynchronous orbit and their solar wind origin,
J. Geophys. Res., 100, 5643,
1995.
Breen, A. R., Z. Mikic, J. A. Linker, A. J. Lazarus, B. J. Thompson,
D. A. Biesecker, P. J. Moran, C. A. Varley,
P. J. S. Williams and
A. Lecinski,
Interplanetary scintillation measurements of the solar wind during Whole Sun
Month: Comparisons with coronal and in situ observations,
J. Geophys. Res., 104, 9847,
1999.
Burke, W. J., D. R. Weimer, and N. C. Maynard,
Geoeffective interplanetary
scale sizes derived from regression analysis of polar cap potentials,
J. Geophys. Res., 104, 9989,
1999.
Chang, S. C., and A. Nishida, Spatial structure of transverse oscillations
in the interplanetary magnetic field,
Astrophysics and Space Science, 23, 301,
1983.
Collier, Michael R., On generating kappa-like distribution functions using
velocity space Lévy flights,
Geophys. Res. Lett., 20,
1531,
1993a.
Collier, Michael R., Energetic particle acceleration in the Jovian
magnetosphere, Ph.D. Thesis, The University of Maryland, College Park,
154 pp., 1993b.
Collier, Michael R., J. A. Slavin, R. P. Lepping, A. Szabo,
and K. Ogilvie,
Timing accuracy for the simple planar propagation of magnetic field
structures in the solar wind,
Geophys. Res. Lett., 25,
2509,
1998.
Couzens, D. A., and J. H. King,
Interplanetary Medium Data Book, Supplement 3, 1977-1985,
National Space Science Data Center (NSSDC),
NSSDC/WDC A-R&S 86-04, 1986.
Crooker, N. U., G. L. Siscoe, C. T. Russell and E. J. Smith,
Factors
controlling degree of correlation between ISEE 1 and ISEE 3 interplanetary
magnetic field measurements,
J. Geophys. Res., 87, 2224,
1982.
Fisher, R., and M. Guhathakurta, Physical properties of polar coronal rays
and holes as observed with the Spartan 201-01 coronograph,
Astrophys. J., 447, L139,
1995.
Frank, L. A., K. L. Ackerson, W. R. Paterson, J. A. Lee,
M. R. English and G. L. Pickett, The Comprehensive Plasma
Instrumentation (CPI) for the Geotail
Spacecraft,
J. Geomagn. Geoelectr., 46, 23,
1994.
Jones, G. H., A. Balogh, and R. J. Forsyth, Radial heliospheric magnetic
fields detected by Ulysses,
Geophys. Res. Lett., 16, 3109,
1998.
Kaymaz, Z., and D. Sibeck, Correlative studies of the solar wind
magnetic field at two near-Earth spacecraft: IMP 8 and ISEE 1,
IUGG 99 Birmingham Abstracts, week A, A.338, 1999.
Kaymaz, Z., and D. Sibeck, Foreshock effects on near Earth
interplanetary magnetic field correlations,
Int. J. Geomagn. Aeron., in press (this issue), 2000.
Kelly, T. J., et al., On the use of a sunward libration-point-orbiting
spacecraft as an interplanetary magnetic field monitor for magnetospheric
studies,
J. Geophys. Res., 91, 5629,
1986.
Kessel, R. L., E. Quintana, and M. Paredo, Local variations of IMF at
Earth's bow shock,
J. Geophys. Res., 104, 24,869,
1999.
Khan, H., and S. W. H. Cowley, Observations of the response time of
high-latitude ionospheric convection to variations in the interplanetary
magnetic field using EISCAT and IMP 8 data,
Annales Geophysicae,
1306,
1999.
King, J. H., Solar wind parameters and magnetospheric coupling studies,
Solar Wind-Magnetosphere Coupling,
edited by Y. Kamide and J. Slavin,
Terra Scientific Publishing Company,
pp. 163-177,
Tokyo,
1986.
Lyons, L. R., et al., Coordinated observations demonstrating external substorm
triggering,
J. Geophys. Res., 102, 27,039,
1997.
Owen, C. J., R. P. Lepping, K. W. Ogilvie, J. A. Slavin,
W. M. Farrell, and
J. B. Byrnes, The lunar wake at 6.8
RL : WIND magnetic field
observations,
Geophys. Res. Lett., 23, 1263,
1996.
Paularena, K. I., G. N. Zastenker, A. J. Lazarus,
and
P. A. Dalin, Solar wind
plasma correlations between IMP 8, INTERBALL 1, and WIND,
J. Geophys. Res., 103, 14,601,
1998.
Priest, E. R., Solar Magnetohydrodynamics,
pp. 19-21, D. Reidel Publishing,
Dordrecht, Holland, 1997.
Richardson, J. D., and K. I. Paularena, The orientation of plasma structure
in the solar wind,
Geophys. Res. Lett., 25, 2097,
1998.
Richardson, J. D., F. Dashevskiy, and K. I. Paularena, Solar wind plasma
correlations between L1 and Earth,
J. Geophys. Res., 103,
14,619,
1998.
Roberts, D. A., and S. Ghosh, A kinematic analysis of the role of velocity
shear in expanding plasmas,
J. Geophys. Res., 104,
22,395,
1999.
Safránková,
J., Z. Nemecek and M. Borák, MAGION 4
observations of bow shock crossings,
Czechoslovak Journal of Physics, 49, 563,
1999.
Schroeder, M., Fractals, Chaos, Power Laws - Minutes from an Infinite Paradise,
pp. 157-160, W. H. Freeman and Company, New York, 1991.
Sibeck, D. G., and J. D. Richardson, Toward forecasting space weather in the
heliosphere,
J. Geophys. Res., 102, 14,721,
1997.
Silverman, N., M. Coplan, F. Ipavich, A. Galvin, K. W. Ogilvie, A. Lazarus,
and J. Steinberg, Solar wind cross correlation measurements between SOHO
and WIND,
EOS (supplement), 78, F603, 1997.
Sotirelis, T., P. T. Newell and Ching-I. Meng, Polar rain as a diagnostic
of recent dayside merging,
J. Geophys. Res., 102, 7151,
1997.
Sonnerup, B. U. Ö., and L. J. Cahill Jr.,
Magnetopause structure and
attitude from Explorer 12 observations,
J. Geophys. Res., 72, 171,
1967.
Zastenker, G. N., M. N. Nozdrachev, J. Safránková, Z. Nemecek,
K. I. Paularena, A. J. Lazarus, R. P. Lepping, and
T. Mukai, Fast solar wind
plasma and magnetic field variations in the magnetosheath,
Czechoslovak Journal of Physics, 49, 579, 1999.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.2.0) on August 4, 2000.

 Nevertheless, we can learn something by examining all cases
together.
Figure 1
shows for all of the two hour data intervals studied in
Collier et al. [1998],
the angular distribution
of the magnetic field direction and how the average peak Crooker hybrid
correlation varies with the average magnetic field direction
projected into the ecliptic plane. The solid data points and line show the
average correlation for all 543 cases (not just the good correlation cases)
falling within that
10o bin.
The minimum average peak Crooker
hybrid correlation coefficient in a
10o bin is 0.519 and the
maximum is 0.710, so that the difference between the minimum and maximum
average peak Crooker hybrid correlation coefficient in a
10o bin
is only 0.191, close to the typical scatter in the data ( 1s ),
indicated by the error bars, so some might argue this effect is not
convincing.
(However, Figure 2
which will be discussed in detail below shows that most
cases of good correlation are around
90o as compared to those at
the Parker spiral direction.)
Nevertheless, we can learn something by examining all cases
together.
Figure 1
shows for all of the two hour data intervals studied in
Collier et al. [1998],
the angular distribution
of the magnetic field direction and how the average peak Crooker hybrid
correlation varies with the average magnetic field direction
projected into the ecliptic plane. The solid data points and line show the
average correlation for all 543 cases (not just the good correlation cases)
falling within that
10o bin.
The minimum average peak Crooker
hybrid correlation coefficient in a
10o bin is 0.519 and the
maximum is 0.710, so that the difference between the minimum and maximum
average peak Crooker hybrid correlation coefficient in a
10o bin
is only 0.191, close to the typical scatter in the data ( 1s ),
indicated by the error bars, so some might argue this effect is not
convincing.
(However, Figure 2
which will be discussed in detail below shows that most
cases of good correlation are around
90o as compared to those at
the Parker spiral direction.)

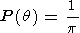


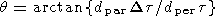
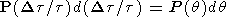
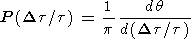
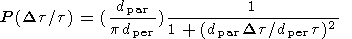
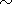 N ).
Thus, increasing the number of measurements will not increase the accuracy of the
measurement. Fundamentally, this is due to the high
probability of very bad timing errors resulting from the tails "throwing
off" the averaging process. However, it raises the intriguing possibility
that the accuracy in determining convection times using two upstream
observations will not improve with multiple measurements - that is there
will be the same uncertainty whether one or a thousand measurements are
made
[Schroeder,
N ).
Thus, increasing the number of measurements will not increase the accuracy of the
measurement. Fundamentally, this is due to the high
probability of very bad timing errors resulting from the tails "throwing
off" the averaging process. However, it raises the intriguing possibility
that the accuracy in determining convection times using two upstream
observations will not improve with multiple measurements - that is there
will be the same uncertainty whether one or a thousand measurements are
made
[Schroeder, 
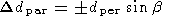
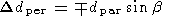
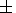 combination selected on the basis of
geometry.
combination selected on the basis of
geometry.
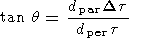
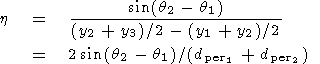





 10-3 RE-1,
implying a typical radius of curvature of 118
RE. Here we quote
unweighted values because weighted values would attach too much importance
to infrequent, well-determined outliers.
10-3 RE-1,
implying a typical radius of curvature of 118
RE. Here we quote
unweighted values because weighted values would attach too much importance
to infrequent, well-determined outliers.
