International Journal of Geomagnetism and Aeronomy
Vol 2, No. 1, June 2000
Hot flow anomalies revisited
S. J. Schwartz
Astronomy Unit, Queen Mary and Westfield College, London,
United Kingdom
G. E. Paschmann, N. Sckopke, and T. M. Bauer
Max-Planck-Institut für
Exterresiche Physik, Garching, Germany
M. W. Dunlop
Space and Atmospheric Physics, Imperial College,
London, United Kingdom
A. N. Fazakerley
Mullard Space Science Laboratory, Holmbury St. Mary,
Dorking, London, United Kingdom
M. F. Thomsen
Los Alamos National Laboratory, Los Alamos, USA
Contents
Abstract
Hot Flow Anomalies (HFAs)
result from the interaction of an interplanetary current
sheet with the Earth's bow shock. The deflected flow and
hot interior of an HFA are
consequences of ions reflected
at the bow shock being channeled along the current
sheet. This process requires a motional electric field
pointing toward the current sheet on at least one side.
Recent reports of a rapid
displacement of the magnetopause by 5
RE as the result of an HFA have led us to
explore the interplanetary conditions
surrounding all reported HFAs. The kinetic
aspects of HFA formation suggest that current
sheets should pass relatively slowly
along the bow shock, that is their normals
should have large cone angles. This
hypothesis is confirmed. The combination
of our results suggests that HFAs
should occur at a rate of several
per day, and thus may play a significant role
in the solar-terrestrial dynamics.
1. Introduction
The discovery in the mid-1980s of regions of hot, highly deflected plasma,
often containing intervals of depressed magnetic fields, near the Earth's bow
shock
[Schwartz et al., 1985;
Thomsen et al., 1986]
sparked a flurry of research activity. Within
several years, these Hot Flow Anomalies (HFAs)
were known to be associated with
the passage of an interplanetary current sheet, and simulations, both test
particle and self-consistent kinetic, confirmed that the injection of particles
reflected at the bow shock, when channeled back upstream under appropriate
field configurations, replicated most, if not all of the observed features.
This state of affairs is reviewed in
Schwartz [1995].
With theory and observation
in accord, and the small, transient, apparently
inconsequential nature of HFAs universally believed,
the subject was considered
closed. However, recent reports
[Sibeck et al., 1998, 1999]
of an HFA which
resulted in a rapid (~7 min)
displacement of the magnetopause by some
5
RE with observable consequences in the ionosphere have
renewed interest in
HFAs.
Sibeck et al. [1999]
point out that the underlying interplanetary current sheet
which appears to have been responsible for this HFA is itself totally
un-remarkable, and thus suggest that such transient but dramatic disturbances
of the magnetosphere are common.
The present paper seeks to address precisely the question of how common HFAs
are by studying the properties of all known HFAs. Additionally, we draw on
multi-mission data where available for supporting information. An enlarged
version of this work is under revision for publication in the Journal of
Geophysical Research.
Burgess [1989]
pursued the relationship of HFAs with an interplanetary current
sheet by studying the behavior of solar wind test particles
specularly reflected at
the bow shock (as observed under quasi-perpendicular shock
geometries
[Sckopke et al., 1983 and references therein]).
When the interplanetary conditions
are such that the motional electric field
E = - V 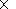 B points toward
the current sheet such
particles are channeled back along the
current sheet into the upstream region.
Fully self-consistent hybrid simulations
by
Thomas et al. [1991]
confirmed this requirement, and showed that the
resulting disturbance was attached to the bow shock,
advanced upstream, and
replicated essentially all the observational features noted above. These
simulations also confirmed earlier claims that HFAs form at tangential
discontinuities (TDs) and not at rotational discontinuities (RDs).
Thomsen et al. [1993]
showed that all 9 reported ISEE HFAs also possessed a
toward-pointing electric field on at least one side.
B points toward
the current sheet such
particles are channeled back along the
current sheet into the upstream region.
Fully self-consistent hybrid simulations
by
Thomas et al. [1991]
confirmed this requirement, and showed that the
resulting disturbance was attached to the bow shock,
advanced upstream, and
replicated essentially all the observational features noted above. These
simulations also confirmed earlier claims that HFAs form at tangential
discontinuities (TDs) and not at rotational discontinuities (RDs).
Thomsen et al. [1993]
showed that all 9 reported ISEE HFAs also possessed a
toward-pointing electric field on at least one side.
The more recent reports by
Sibeck et al. [1999]
suggest that the IMF current sheet
appears to be unremarkable, implying that HFAs should be as common as
interplanetary TDs (~0.6 per hour
[Lepping and Behannon, 1986])
and represent a
perhaps non-negligible
perturbation of the magnetosphere. The question we wish to
address here is, therefore, whether there other restrictions
as to which IMF TDs
give rise to HFAs.
2. The Dataset
Our set of 30 HFAs includes all previously reported events based on AMPTE
UKS, AMPTE IRM, ISEE 1/2,
and Interball spacecraft, together with a few new
AMPTE events. References describing the spacecraft and
instrumentation can be found in the comprehensive HFA publications
[Paschmann et al., 1988;
Schwartz et al., 1988;
Sibeck et al., 1999;
Thomsen et al., 1988].
3. HFA Environments
We seek here to characterize the interplanetary environment accompanying our
set of HFAs in order to
determine what special circumstances might be necessary to
provoke HFA formation.
3.1. Statistical Properties
Several parameters
of the HFA environments may play some role in HFA formation.
These include
local shock
geometry before and after HFA passage and the cone angle of the IMF
current sheet with respect to the Sun-Earth line, which in turn provides an
estimate of the speed of transit of the
current sheet-bow shock intersection
along the bow shock.
The presence of the large disturbance associated with the HFA precludes the use
of minimum variance analysis to determine the tangential/rotational nature of
the underlying interplanetary discontinuity.
Following previous practice and
guided by the negative simulational
results in the case of an RD found by
Thomas et al. [1991],
we calculate the current sheet normal
as the cross-product between pre- and post-HFA fields, as appropriate
for a TD.
 The determination of whether a discontinuity is a TD or an RD
traditionally requires testing the size of the magnetic field
normal to the
current sheet,
Bn, and the jump in field magnitude from pre- to
post-current sheet
[Neugebauer et al., 1984].
Estimating
Bn involves a minimum
variance analysis through the current
sheet which, as noted above, we cannot do.
However, a summary of the jump in field
magnitude is presented in
Figure 1.
Over 2/3rds of all HFAs have jumps less than
0.2, which would have precluded their positive
identification as TDs in the
historical discontinuity literature
[Neugebauer et al., 1984].
Lepping and Behannon [1986]
suggest, however, that the
full population of discontinuities
does indeed include a "mixed'' group which
supplies a similar proportion of TDs with small jumps in field magnitude.
The determination of whether a discontinuity is a TD or an RD
traditionally requires testing the size of the magnetic field
normal to the
current sheet,
Bn, and the jump in field magnitude from pre- to
post-current sheet
[Neugebauer et al., 1984].
Estimating
Bn involves a minimum
variance analysis through the current
sheet which, as noted above, we cannot do.
However, a summary of the jump in field
magnitude is presented in
Figure 1.
Over 2/3rds of all HFAs have jumps less than
0.2, which would have precluded their positive
identification as TDs in the
historical discontinuity literature
[Neugebauer et al., 1984].
Lepping and Behannon [1986]
suggest, however, that the
full population of discontinuities
does indeed include a "mixed'' group which
supplies a similar proportion of TDs with small jumps in field magnitude.
Interestingly, there are cases where the RD/TD distinction is already
better established. These include the simulations
[Thomas et al., 1991]
and the
Interball HFA with upstream data from WIND
[Sibeck et al., 1999].
These all
report underlying
TDs in which there is little or no change in field magnitude.
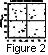 Figure 2
presents the local shock geometry before and
after the HFA. The figure
reveals a slight tendency for pre-HFA bow shocks to be more quasi-parallel and
post-HFA shocks more quasi-perpendicular. Interestingly, at least near
the local point of observation relatively few HFAs correspond to
quasi-perpendicular conditions on both sides, and several HFAs have
quasi-parallel shocks on both sides. This may indicate that these HFAs were
formed at a quasi-perpendicular environment some distance from the point of
observation. Alternatively, intermittent ion reflection under quasi-parallel
shock conditions
[Gosling et al., 1982]
may be sufficient to promote some local
HFA development.
Figure 2
presents the local shock geometry before and
after the HFA. The figure
reveals a slight tendency for pre-HFA bow shocks to be more quasi-parallel and
post-HFA shocks more quasi-perpendicular. Interestingly, at least near
the local point of observation relatively few HFAs correspond to
quasi-perpendicular conditions on both sides, and several HFAs have
quasi-parallel shocks on both sides. This may indicate that these HFAs were
formed at a quasi-perpendicular environment some distance from the point of
observation. Alternatively, intermittent ion reflection under quasi-parallel
shock conditions
[Gosling et al., 1982]
may be sufficient to promote some local
HFA development.
 The suggestion by
Burgess [1989]
that toward/away motional electric fields
played a key role in HFA formation, confirmed by the simulations of
Thomas et al. [1991],
received observational support by
Thomsen et al. [1993].
We
repeat that test here in
Figure 3.
With our
convention that
ncs
The suggestion by
Burgess [1989]
that toward/away motional electric fields
played a key role in HFA formation, confirmed by the simulations of
Thomas et al. [1991],
received observational support by
Thomsen et al. [1993].
We
repeat that test here in
Figure 3.
With our
convention that
ncs  Vsw
< 0,
the angle between a toward electric
field and
ncs should be
< 90
o in the pre-HFA region and
> 90
o in the post-HFA region. The figure
confirms again the requirement that at least
one side of the interplanetary current sheet possesses a toward field.
Vsw
< 0,
the angle between a toward electric
field and
ncs should be
< 90
o in the pre-HFA region and
> 90
o in the post-HFA region. The figure
confirms again the requirement that at least
one side of the interplanetary current sheet possesses a toward field.
 The HFA normals have a very pronounced distribution in cone
angle as shown in Figure 4
by comparison with general
TD survey results. This provides the first clear indication that not every
interplanetary tangential discontinuity results in HFA formation. Normals with cone
angles above
60o account for over 80%
of all HFAs but only 30% of all TDs.
The HFA normals have a very pronounced distribution in cone
angle as shown in Figure 4
by comparison with general
TD survey results. This provides the first clear indication that not every
interplanetary tangential discontinuity results in HFA formation. Normals with cone
angles above
60o account for over 80%
of all HFAs but only 30% of all TDs.
3.1.5. Current sheet-bow shock intersection.
Here we investigate the speed of transit
Vtr of the current sheet bow shock intersection (line)
along the bow shock; the
calculation only involves components in the plane containing the normals to the
bow shock and the current sheet (both taken as planar). The ratio of
Vtr to
the gyrospeed
Vg of an ion (specularly) reflected at the bow shock determines
whether the transit speed is sufficiently slow for the ions
to be channeled along
the shock. This ratio depends only on geometric factors and can be written
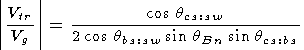 | (1) |
where
qbs:sw [
qcs:sw ]
is the angle between the bow shock
normal [current sheet normal] and
solar wind velocity and
qcs:bs is the angle
between the current sheet and bow shock.
If all the angles in (1) are
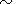 45o this ratio is ~1.
45o this ratio is ~1.
 Figure 5 shows a histogram of the minimum (pre-HFA or
post-HFA)
normalized transit speed. As expected from
Figure 4,
this
ratio is small ( < 0.5)
on at least one side of all but 10% of the HFAs in the
present study. Two-thirds of the HFAs have normalized
transit speeds less than 0.3.
Figure 5 shows a histogram of the minimum (pre-HFA or
post-HFA)
normalized transit speed. As expected from
Figure 4,
this
ratio is small ( < 0.5)
on at least one side of all but 10% of the HFAs in the
present study. Two-thirds of the HFAs have normalized
transit speeds less than 0.3.
3.2. Multi-Mission Case Studies
A partial resolution of the RD/TD/Either dilemma posed in
Section 3.1.1.
above is to identify the same interplanetary
current sheet further upstream of the bow shock, where the HFA disturbance is
absent. We have found 4 such
cases. The general timing delays and pre/post-HFA IMF conditions are similar to
those at the HFA observation location. All 4 cases show discontinuities with
small
normal components, consistent with identification as TDs, though in most cases the
small jump in
| B| is also present. However, several of the discontinuities
observed upstream away from the HFA location show significant
dips in field
magnitude in
the interior of the current sheet. This property strengthens the TD
identification.
3.3. HFA rate of occurrence
We can now estimate the rate of occurrence of HFAs by assuming that all TDs
above
60o cone angles with a toward electric field on at least one side
result in HFAs. The overall interplanetary directional
discontinuity rate at 1 AU
is ~1.25
per hour of which a fraction
0.89/1.89 = 47% are TDs
[Lepping and Behannon, 1986].
Assuming equal probabilities for positive and
negative interplanetary field polarities, 3/4 of these TDs should have a
toward-pointing
E
on at least one side. We estimate the HFA rate of occurrence as:
0.3 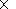 1.25
1.25 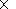 0.47
0.47 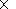 0.75 = 0.13 per hour or 3.2 HFAs per day.
This rate is entirely consistent with the number (20) of HFAs
AMPTE IRM observed in its first year of operations when the orbital and
operational aspects are taken into account.
0.75 = 0.13 per hour or 3.2 HFAs per day.
This rate is entirely consistent with the number (20) of HFAs
AMPTE IRM observed in its first year of operations when the orbital and
operational aspects are taken into account.
4. Conclusions
Treating the 30 HFAs used in this study as representative, we conclude that
HFAs should be relatively common. The
conditions for HFA formation include:
- an interplanetary current sheet with a motional electric field which
points toward it on at least one side;
- current sheets whose normals make a large cone angle with the sunward
direction;
- tangential discontinuities (probably).
Moreover, HFA formation appears to be favored by:
- discontinuities with a relatively small jump in field
magnitude from one side to the other;
- quasi-perpendicular bow shock conditions on at least one side, and
preferentially the post-HFA side.
The fact that several HFAs locally have quasi-parallel conditions on both sides
suggests that they survive well beyond their region of formation.
The above conditions, when compared against known statistics of interplanetary
directional discontinuities, suggest that HFAs should occur at a rate of
~3 per day. The degree of disruption of the bow shock/magnetopause
observed
in association with one HFA
[Sibeck et al., 1999]
suggests that HFAs are
more consequential than
originally envisaged in terms of their dynamic impact on
the dayside magnetosphere.
There remain several questions which require multi-point
measurements. What
portion of the bow shock is involved during the lifetime of an HFA? Is it
simply related to the criteria listed above when applied to the curved bow
shock? What is the shape of the resulting disturbance? This study has also
highlighted the need to develop better analysis tools to separate tangential
and rotational discontinuities particularly when the jump in field magnitude is
small.
Acknowledgments
This work was
initiated and conducted as part of a Science Team hosted by the
International Space Science Institute in Bern, Switzerland. We gratefully
acknowledge the warm hospitality and excellent facilities provided by ISSI and
its staff. Much of the data exchange was greatly eased by the use and support
of the UK CDHF for STP, a joint RAL/QMW venture; Chris Perry (RAL) and Tony
Allen (QMW) were key to this effort. Supporting data and information was drawn
from several excellent www facilities, including the UCLA ISEE magnetometer
archives (R. Strangeway), IMP 8 archives at NSSDC's NDADS facility (RP Lepping,
magnetometer PI), and the SSC at NSSDC. SJS's contributions were supported in
part by the PPARC and conducted while enjoying the amicable environment and
support of CESR/CNRS, Toulouse.
References
Burgess, D., On the effect of a tangential discontinuity on ions specularly
reflected at an oblique shock,
J. Geophys. Res., 94,
472,
1989.
Gosling, J. T., M. F. Thomsen, S. J. Bame, W. C. Feldman, G. Paschmann,
and
N. Sckopke, Evidence for specularly reflected ions upstream from the
quasi-parallel bow shock,
Geophys. Res. Lett., 9, 1333,
1982.
Lepping, R. P., and K. W. Behannon, Magnetic field directional discontinuities:
Characteristics between 0.46 and 1.0 AU,
J. Geophys. Res., 91, 8725,
1986.
Neugebauer, M., D. R. Clay, B. E. Goldstein, B. T. Tsurutani, and
R. D. Zwickl,
A reexamination of rotational and tangential discontinuities in the solar
wind,
J. Geophys. Res., 89, 5395,
1984.
Paschmann, G., G. Haerendel, N. Sckopke, E. Möbius, H. Lühr,
and C. W.
Carlson, Three-dimensional plasma structures with anomalous flow directions
near the Earth's bow shock,
J. Geophys. Res., 93,
11,279,
1988.
Schwartz, S. J., Hot flow anomalies near the
Earth's bow shock,
Adv. Space Res., 15, 107,
1995.
Schwartz, S. J., R. L. Kessel, C. C. Brown, L. J. C. Woolliscroft,
M. W.
Dunlop, C. J. Farrugia, and D. S. Hall, Active current sheets near the
Earth's bow shock,
J. Geophys. Res., 93, 11,295,
1988.
Schwartz, S. J., et al., An active current sheet in the solar wind,
Nature, 318, 269,
1985.
Sckopke, N., G. Paschmann, S. J. Bame, J. T. Gosling, and C. T. Russell,
Evolution of ion distributions across the nearly perpendicular bow shock -
specularly and non-specularly reflected-gyrating ions,
J. Geophys. Res., 88, 6121,
1983.
Sibeck, D. G., N. L. Borodkova, G. N. Zastenker, S. A. Romanov,
and J. A.
Sauvaud, Gross deformation of the dayside magnetopause,
Geophys. Res. Lett., 25, 453,
1998.
Sibeck, D. G., et al., Comprehensive study of the magnetospheric response
to a
hot flow anomaly,
J. Geophys. Res., 104, 4577,
1999.
Thomas, V. A., D. Winske, M. F. Thomsen, and T. G. Onsager, Hybrid
simulation
of the formation of a hot flow anomaly,
J. Geophys. Res., 96,
11,625
1991.
Thomsen, M. F., J. T. Gosling, S. A. Fuselier, S. J. Bame, and
C. T. Russell,
Hot, diamagnetic cavities upstream from the Earth's bow shock,
J. Geophys. Res., 91, 2961,
1986.
Thomsen, M. F., J. T. Gosling, S. J. Bame, K. B. Quest, C. T. Russell,
and
S. A. Fuselier, On the origin of hot diamagnetic cavities near the Earth's
bow shock,
J. Geophys. Res., 93, 11,311,
1988.
Thomsen, M. F., V. A. Thomas, D. Winske, J. T. Gosling, M. H.
Farris, and C. T.
Russell, Observational test of hot flow anomaly formation by the interaction
of a magnetic discontinuity with the bow shock,
J. Geophys. Res.,
98, 15,319,
1993.
Turner, J. M., On the relation between solar wind structure and solar wind
rotational and tangential discontinuities,
J. Geophys. Res., 78, 59, 1973.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.2.0) on August 3, 2000.
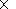 B points toward
the current sheet such
particles are channeled back along the
current sheet into the upstream region.
Fully self-consistent hybrid simulations
by
Thomas et al. [1991]
confirmed this requirement, and showed that the
resulting disturbance was attached to the bow shock,
advanced upstream, and
replicated essentially all the observational features noted above. These
simulations also confirmed earlier claims that HFAs form at tangential
discontinuities (TDs) and not at rotational discontinuities (RDs).
Thomsen et al. [1993]
showed that all 9 reported ISEE HFAs also possessed a
toward-pointing electric field on at least one side.
B points toward
the current sheet such
particles are channeled back along the
current sheet into the upstream region.
Fully self-consistent hybrid simulations
by
Thomas et al. [1991]
confirmed this requirement, and showed that the
resulting disturbance was attached to the bow shock,
advanced upstream, and
replicated essentially all the observational features noted above. These
simulations also confirmed earlier claims that HFAs form at tangential
discontinuities (TDs) and not at rotational discontinuities (RDs).
Thomsen et al. [1993]
showed that all 9 reported ISEE HFAs also possessed a
toward-pointing electric field on at least one side.



 Vsw
< 0,
the angle between a toward electric
field and
ncs should be
< 90
o in the pre-HFA region and
> 90
o in the post-HFA region. The figure
confirms again the requirement that at least
one side of the interplanetary current sheet possesses a toward field.
Vsw
< 0,
the angle between a toward electric
field and
ncs should be
< 90
o in the pre-HFA region and
> 90
o in the post-HFA region. The figure
confirms again the requirement that at least
one side of the interplanetary current sheet possesses a toward field.

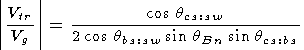
 45o this ratio is ~1.
45o this ratio is ~1.
