International Journal of Geomagnetism and Aeronomy
Vol 1, No. 2, November 1998
Indices for monthly median foF2 and
M(3000)F2 modeling and long-term prediction:
Ionospheric index MF2
A. V. Mikhailov
Institute for Terrestrial Magnetism, Ionosphere, and Radio
Wave Propagation, Troitsk, Moscow Region, Russia
V. V. Mikhailov
Institute of Applied Geophysics, Moscow, Russia
Contents
Abstract
An improved ionospheric index
MF2 is compared with
traditional sunspot number
R and ionospheric
IG,
IF2,
T indices
used for ionospheric modeling and long-term prediction. Regression
analysis of monthly median
foF2 and
M(3000)F2 versus these indices
(monthly and 12-month running mean) has shown the advantage of
MF2 over smoothed indices used in practice and a comparable accuracy
with monthly ionospheric indices. Different indices ( MF2 for
foF2 and
R12 for
M(3000)F2 ) may be recommended for practical use.
This results from different
NmF2 and
hmF2 dependence on main
aeronomic parameters responsible for the
F2 region formation.
Monthly index
MF2 can be predicted in the long-term with acceptable
accuracy due to its regularity in seasonal and solar cycle
variations. The proposed method for monthly
MF2 index long-term
prediction is based on a relationship with smoothed ionospheric
indices
IG12,
MF212,
IF212 or sunspot number
R12, which is
predicted and disseminated by
the International Radio Consultative Committee (CCIR).
MF2 index prediction is made
for solar cycle 23. Long-term
foF2 prediction based on the
MF2 index for solar cycle 21 is shown to improve prediction
accuracy by 30% on average compared with the CCIR approach based on
sunspot number
R12.
Introduction
Empirical ionospheric modeling and prediction widely use various
indices to specify the variations of ionospheric parameters.
Monthly, weekly, daily, and even hourly indices are used in
practice
[Bradley, 1993;
International Radio Consultative Committee (CCIR), 1990;
Mikhailov et al., 1990a;
Secan and Wilkinson, 1997;
Turner and Wilkinson, 1979;
Wilkinson, 1986a].
The idea of
index use is based on the assumption that key ionospheric
characteristics, such as
foF2,
M(3000)F2,
foF1, and
foE, are associated
in a systematic way with certain measurable quantities concerned
with solar and geomagnetic activity. However, different indices
should be used for
F2,
F1, and
E layer parameters
[CCIR, 1990],
because physical mechanisms of their formation are
different and independent to a great extent. The same is valid for
foF2 and
M(3000)F2. Usually it is assumed that what is best for
foF2 should also be best for
M(3000)F2, but this is not obvious.
For instance, the dependence of
foF2 and
hmF2 on atmospheric
parameters is different, and one may expect that different indices
may turn out to be the best for
foF2 and
M(3000)F2.
Direct solar indices take into account solar activity level
expressed either by traditional sunspot number
R (usually a
12-month running mean
R12 is used) or by solar radiation in
selected spectral intervals (like
F10.7 or
I58.4 ). Keeping in
mind the physical mechanism of the
F2 region formation, the sunspot
number
R12 is far from being the best index for
foF2. It is not
related directly to solar EUV radiation which is responsible
for the ionization and to a great extent for the state of the upper
atmosphere at
F2 layer heights. Research adherence to
R12 as the input parameter for empirical ionospheric
models like those of
CCIR [1967-1990]
or
Chernyshov and Vasil'eva [1973]
probably is explained by the fact that long and
continuous observations were available only on sunspot numbers at
the time that these models were developed.
The ionospheric
F2 region is
known to be governed by solar ionization radiation, highly variable
thermospheric neutral composition, and dynamical processes. That is
why there is no one-to-one relationship for
foF2 with any direct
solar index. A well-known effect of hysteresis in solar cycle
foF2 variations
[Rao and Rao, 1969;
Smith and King, 1981]
may result in a 1-MHz difference for annual mean
foF2 at the same
R12. For a particular month the
difference may be even higher: up to 1.5 MHz
[Mikhailov, 1993].
This means that
foF2 versus
R12 regression
accuracy cannot be improved in principle as it is limited by this
hysteresis effect. A physical explanation for the hysteresis type of
solar cycle
foF2 variation is proposed by
Mikhailov and Mikhailov [1994, 1995a],
but it is stressed that the effect
may be considered as a result of improper solar index application.
The other problem with
R12 use is the "saturation effect" at
high solar activity level. According to CCIR recommendations
[CCIR, 1967-1990]
also used in the International Reference Ionosphere (IRI)
[Bilitza, 1990],
a linear relationship between
R12 and monthly median
foF2 should
be used for
R12 < 150 and unchanged
foF2 for
R12 > 150 throughout the solar cycle. But linear
dependence is not valid in
many cases, and the recommended limitation on
foF2 at high solar
activity can give large errors in
foF2 prediction
[Mikhailov, 1993].
Despite all difficulties with
R12, it is
considered the basic index of solar activity for ionospheric
modeling and prediction, and other indices are related to
R12 (see the references of
Bradley [1993]).
Since the end of the 1940s solar radio emission at
l = 10.7 cm
was measured regularly, the
F10.7 index, expressed in units of
10-22 W m-2 Hz-1,
is widely used in aeronomy as an
indicator of solar activity level. All modern thermospheric models
as well as models of solar EUV radiation are based on the index
F10.7. This is due to the fact that solar radio
emission at
l = 10.7 cm is generated in about the same
areas on the Sun as EUV
radiation responsible to a great extent for the state of the upper
atmosphere and ionosphere. Nevertheless, analysis
[CCIR, 1990;
Kouris et al., 1994;
Mikhailov et al., 1990a]
has shown that the use of monthly or 12-month
running mean
F10.7 values instead of
R12 does not improve
essentially the
foF2 versus solar activity regression accuracy.
The use of solar flux at
l = 58.4 nm, which is proportional
to the total flux in the spectrum range of
l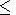 100 nm
as an
index for
foF2 regression, turned out to be not very efficient
[Mikhailov et al., 1990a].
A similar conclusion follows from
analysis of results obtained by
Lakshmi et al. [1988],
where the dependence of
foF2 versus the measured solar flux in
the
l= 17-19 nm interval was used. Such results
are not surprising,
as
solar EUV radiation reflects only one side of the
F2 region
formation, namely,photoionization. From this point of view, the
traditional 12-month running mean sunspot number
R12 seems to be
more preferable than other direct solar indices as it serves
implicitly as an indicator not only of ionization efficiency, but
of the overall state of the upper atmosphere. On the other hand, it
should be kept in mind that the
foF2 versus
R12 regression
accuracy can be improved using a nonlinear dependence instead of
a linear one
[Jones and Obitts, 1970;
Mikhailov, 1993],
and so
R12 can be efficiently used in practice.
100 nm
as an
index for
foF2 regression, turned out to be not very efficient
[Mikhailov et al., 1990a].
A similar conclusion follows from
analysis of results obtained by
Lakshmi et al. [1988],
where the dependence of
foF2 versus the measured solar flux in
the
l= 17-19 nm interval was used. Such results
are not surprising,
as
solar EUV radiation reflects only one side of the
F2 region
formation, namely,photoionization. From this point of view, the
traditional 12-month running mean sunspot number
R12 seems to be
more preferable than other direct solar indices as it serves
implicitly as an indicator not only of ionization efficiency, but
of the overall state of the upper atmosphere. On the other hand, it
should be kept in mind that the
foF2 versus
R12 regression
accuracy can be improved using a nonlinear dependence instead of
a linear one
[Jones and Obitts, 1970;
Mikhailov, 1993],
and so
R12 can be efficiently used in practice.
Ionospheric indices are derived from observed trends in
ionospheric characteristics measured by the worldwide ionosonde
network. Two types of ionospheric indices exist: truly ionospheric
indices such as
IF2 [Minnis, 1955;
Minnis and Bazzard, 1960],
the Australian index
T [Caruana, 1990;
Turner, 1968],
and index
MF2 [Mikhailov and Mikhailov, 1995b]
and model-oriented indices such as
IG [Liu et al., 1983],
and RESSN
[Mikhailov et al., 1990b].
All ionospheric indices
except for
MF2 give effective sunspot numbers which provide the
best regression accuracy for
foF2 in the course of a solar cycle.
The
MF2 index is
an effective noon
foF2 over the northern hemisphere
normalized by a magnetic factor
M.
Model-oriented
indices are developed to work with particular empirical models:
IG with
the
CCIR [1967-1990]
model and RESSN with MUF Forecast
[Chernyshov and Vasil'eva, 1973],
used for HF communication
prediction. All ionospheric indices (especially monthly) were shown
to provide much better regression accuracy in comparison with to
R12 for
monthly
foF2 [Liu et al., 1983;
Mikhailov et al., 1990a, 1996;
Wilkinson, 1986b].
But there is a problem with using ionospheric indices in practice. Only
smoothed 12-month running mean indices can be
predicted
in the long-term
with acceptable accuracy, but the regression of
foF2 with such
smoothed indices is not as good as with monthly ones. Thus the
overall accuracy gain with ionospheric indices use instead of
R12 is not too high: about 11% for predictions
6 months in
advance and 18% for predictions 12 months in advance for
IG12 [Liu et al., 1983]
and about 13% when RESSEN
12 was
used
[Mikhailov et al., 1990b].
So the problem is to
derive such an ionospheric index which could demonstrate the merits
of monthly indices (that is high regression accuracy of
foF2 with
solar activity) and which could be
predicted
in the long-term
(1-12 months in
advance) with acceptable accuracy as well.
An attempt to produce an appropriate ionospheric index
MF2 was
undertaken in the framework of the European PRIME (COST-238)
project by
Mikhailov and Mikhailov [1995b].
This new index
was used to develop monthly median
foF2 and
M(3000)F2 ionospheric
model
MQMF2 over Europe
[Mikhailov et al., 1996].
Comparison of
MQMF2 with the CCIR model (based on
R12 ) in a
retrospective mode (16,000-18,000 comparisons) gave an overall
standard deviation decrease by 30-50%. Comparison with the CCIR
approach for long-term (3-12 months in advance) predictions for the
rising phase of solar cycle 22 gave essential improvement of
prediction accuracy when the
MF2 index was used. So this proposition
seems to be very promising and is worthy of further development.
The aim of this paper is to try to improve the
MF2 index by taking into
account additional ionosonde observations, to make a comparison
with other direct and ionospheric indices used in practice, and to
propose a method for
MF2 long-term prediction convenient for
practical use.
Improved Index MF2
The idea of
MF2 index derivation is given by
Mikhailov and Mikhailov [1995b].
The only difference of the new approach is
in using the Chapman function of the solar zenith angle instead of
cosc for the "magnetic factor"
M [Besprozvannaya, 1966;
Rothwell, 1962]
calculation. This allowed us to include
additional high-latitude ionosonde stations in the procedure of
index derivation. So the new index
MF2 is found using the following
expressions:
foF2/M = f(Ch cL)
M = (Ch cL/ Ch
cMC)0.25
cL and
cMC being solar
zenith angles at a given and
magnetically conjugate points at the same UT moment. The reduction
foF2 by
M factor gets in order to some extent
foF2 data on
ionosonde stations located in different latitudinal and
longitudinal zones. The new index
MF2 is defined as the
foF2/M value
found for an optimum
Chc which is so chosen for each month that
the standard deviation in the
foF2 versus
MF2 regression overall for
the ionosonde stations is minimized. Monthly indices
MF2 for
1945-1996 are listed in Table 1.
 Monthly indices
MF2 show the regularity in seasonal and solar cycle
variations, and this feature is used in the
MF2 index prediction
method (see below). Figure 1 shows an example of this regularity in
MF2 variations during the 1969-1979 decade. Well-pronounced
semiannual peaks with relative minima during solstice periods are
similar to midlatitude median
foF2 variations. The difference is
seen in annual variations: unlike monthly median
foF2, summer
MF2 values are higher than winter ones. The "winter anomaly" effect for
MF2 takes place only during years of very high solar activity
(1957-1958 and 1990-1991; see Table 1). Ionospheric index
T variations are given in Figure 1 for comparison. Unlike
MF2,
monthly index
T does not show as a rule any regularity in its
variation.
Monthly indices
MF2 show the regularity in seasonal and solar cycle
variations, and this feature is used in the
MF2 index prediction
method (see below). Figure 1 shows an example of this regularity in
MF2 variations during the 1969-1979 decade. Well-pronounced
semiannual peaks with relative minima during solstice periods are
similar to midlatitude median
foF2 variations. The difference is
seen in annual variations: unlike monthly median
foF2, summer
MF2 values are higher than winter ones. The "winter anomaly" effect for
MF2 takes place only during years of very high solar activity
(1957-1958 and 1990-1991; see Table 1). Ionospheric index
T variations are given in Figure 1 for comparison. Unlike
MF2,
monthly index
T does not show as a rule any regularity in its
variation.
Comparison of Indices
Two kinds of
MF2 index comparison with other indices should be
done: (1) a comparison with monthly ionospheric indices which are
known to provide the best regression accuracy for
foF2 with solar
activity level and (2) a comparison with smoothed 12-month running
mean indices which are used in practice for
foF2 and
M(3000)F2 modeling and long-term prediction. In both
cases, we will analyze
the regression accuracy of
foF2 (or
M(3000)F2 ) versus any chosen
index. A polynomial of the third degree is used for the regression
[Mikhailov, 1993].
A special procedure was developed to
prevent the regression curve from unnatural behavior at the ends of
the index interval (at low and high solar activity). Although such
model-oriented indices as
IG are supposed to be used with their own
"mother" models, they may be considered independently as well for
our regression analysis like other indices. We will operate with
standard
e (in megahertz) and relative mean
d (in percent)
deviations given by expressions
e =[ (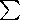 D2 - (
D2 - (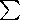 D)2/n) / (n-1)]0.5
D)2/n) / (n-1)]0.5
d = [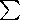 |D
/foF2 obs|] /n
|D
/foF2 obs|] /n
where
D = foF2 pred
- foF2 obs.
The results of the regression analysis of the first type are
given
in Table 2
for the ionosonde station Arkhangelsk (64.6o N,
40.5o E). Monthly ionospheric indices
IF2,
IG,
T ,
MF2 (old
version by
Mikhailov and Mikhailov [1995b]), and
MF2 (new
version, Table 1)
along with the traditional
R12 were used for
comparison. Three parts of the day, three seasons, and three levels
of solar activity during the 1957-1990 period were analyzed. The
number of comparisons (ranging from 1600 to 3100 depending on
conditions) is sufficient to consider the results statistically
significant. The analysis shows that new and old
MF2 indices give
very close results, being a little bit more efficient than
IF2 and
IG. Index
T is comparable with
MF2 and turns out to be even more
efficient in some cases. Index
R12 is systematically worse than
MF2, by 27% on average. The main result of this comparison is that
the newly developed index
MF2 is as efficient as the other
monthly ionospheric indices.
The second type of comparison is made with smoothed 12-month
running mean indices
R12,
IF212 ,
IG12, and
T12 which are
really used in practice for long-term HF radio communication
predictions (Table 3). Some additional stations (Sofia, Sverdlovsk)
were used in the analysis and gave similar results not listed here.
The results of similar comparison for Moscow, Slough, Uppsala, and
Athens ionosonde stations with the old version of the
MF2 index may be
found in the work of
Mikhailov et al. [1996].
The results of
MF2 comparison with smoothed 12-month running mean
indices show that the
MF2 index provides systematically better
regression accuracy than any index in question, either direct
solar ( R12 ) or ionospheric. The other result is that
smoothed
ionospheric indices give rather little accuracy improvement compared
with
R12.
The analysis has shown that such well-known
effects in
foF2 solar
cycle variations as "saturation" at high solar activity and
"hysteresis" in the course of a solar cycle related with
R12 use are absent when the
MF2 index is applied. This advantage of
the use of ionospheric indices
over direct solar indices was pointed out
earlier by
Mikhailov and Mikhailov [1994].
Similar regression analysis was made for the
M(3000)F2 parameter. It
should be kept in mind that
M(3000)F2 data are much less reliable
compared with
foF2 and they are not consistent at some ionosonde
stations. A comparison with inconsistent
M(3000)F2 data may result
in a wrong conclusion about the tested index. So a thorough
examination was made to select reliable stations for further index
comparison. Among them is Lannion (48.45o N, 356.73o E);
the results on this station for the period 1957-1990 are given in
Table 4.
The results of our comparison for various geophysical conditions
show that traditional sunspot number
R12 provides the best
overall regression accuracy in comparison with other indices. The
gain is noticeable especially during daytime, equinox, and high
solar activity. Only
MF2 provides comparable accuracy in some
conditions; the other indices are systematically worse. Similar
results were obtained for some other European ionosondes.
Long-Term Prediction of Monthly MF2
Using the regularity in the
MF2 index seasonal and solar cycle
variations similar to monthly median
foF2 changes (Figure 1), a
method for its long-term prediction can be proposed. It is based on
the
MF2 relationship with any smoothed index
R12,
IG12,
IF212, or
MF212.
Analysis has shown that the best results can be
obtained if
different phases of the solar cycle
are
analyzed
separately
for each month. The period of 1957-1988 was chosen for the
analysis when the amount of ionosonde observations was sufficient
to get monthly
MF2 with the highest accuracy. Three phases of the solar
cycle
were considered:
minimum plus rising phases (1963-1967, 1975-1978,
1985-1988), maximum phase (1957-1959, 1968-1970, 1979-1981),
and falling plus minimum phases (1960-1965, 1971-1976,
1982-1986).
The results of regression analysis are
given in Table 5.
It is seen that
MF2 obtained from
R12,
IG12,
IF212, or
MF212 can be found with prediction accuracy ranging
from 2.2 to
3.6%, which may be considered acceptable for practical use.
Ionospheric indices provide better accuracy than
R12. Long-term
prediction of
MF212 can be carried out using the well-known
McNish and Lincoln [1949]
method, as four complete solar cycles
of observed
MF2 indices are available now. It should be stressed
that Table 5
gives an estimate of the maximal accessible accuracy
as it was obtained in retrospective mode for observed smoothed
indices.
Using the
MF2 with
R12 relationship, a forecast of
MF2 indices
was made for solar cycle 23 (Table 6).
Space Environment Center (SEC)
prediction of
smoothed sunspot numbers
R12 [Space Environment Center, 1997]
was used for
MF2 calculations.
The final goal of all index considerations is to improve the
prediction accuracy for monthly
foF2 and
M(3000)F2. To estimate the
efficiency of the proposed approach, we performed
foF2 long-term
predictions for solar cycle 21 (1977-1985) using officially
predicted
R12 values. The
R12 forecast 3, 6, and 12 months in
advance published in Solar-Geophysical Data was used to
calculate
MF2 indices. The accuracy of the official
R12 forecast
and our
MF2 index prediction for the 1977-1985 period is given in
Table 7.
Table 7
shows that the prediction accuracy falls with increasing
the lead time by a factor of 2 for
R12 and by 1.37 for
MF2 when
12- and 3-month forecasts are compared. This means that
MF2 is less
sensitive to errors in
R12 predictions. Naturally, the accuracy
of
MF2 indices obtained in a truly prediction mode is less than the
maximal (Table 7).
These predicted
MF2 indices were used as input
to the
MQMF2 model
( Mikhailov et al., [1996])
for
the midlatitude ionosonde station Kaliningrad (54.7o N,
20.62o E) to calculate monthly
foF2. The same
foF2 calculations
were made with the CCIR model (based on the
R12 index) using the
officially predicted
R12. The results of comparison with
foF2 observations for four UT moments are given in
Table 8.
Discussion
Ionospheric indices are known to be advantageous in comparison with
direct
solar ones. They provide better regression accuracy for
foF2 versus
solar activity; the saturation effect at high solar activity level
and the hysteresis-type solar cycle variation of
foF2 are avoided
with monthly ionospheric indices use.
Smoothed
ionospheric
indices can be
predicted more accurately than the traditional sunspot number
R12 [Liu et al., 1983].
All of these merits of ionospheric
indices are due to the fact that
ionosphere works as a smoothing filter and
ionospheric indices reflect the entire impact of all processes in
the
F2 region. It should be mentioned that the efficiency of some
of these physical processes is not yet well known.
The proposed index
MF2 seems to solve the dilemma between
regression accuracy and long-term predictability.
The monthly index
MF2 provides as a high regression accuracy as the other monthly
ionospheric indices (Table 2), which are not
predicted
in the long term,\linebreak
\noindent and much better regression accuracy in comparison
with 12-month
running mean indices (Table 3), which are predicted in the long term.
The monthly
MF2 index shows a regularity in seasonal and solar cycle
variations similar to monthly median
foF2 and can be
predicted
in the long term
using the relationship with smoothed predictable
R12,
IG12, and
IF212 indices. Officially long-term predicted
ionospheric
IG12 or
IF212 indices
by CCIR
may be recommended to
get
MF2, as they provide better accuracy than
R12 does. But even
the use of
R12 for
MF2 prediction can improve the
foF2 long-term
prediction accuracy by 30% on average compared with the CCIR approach,
as was shown for solar cycle 21 at Kaliningrad station. This
result is much better than can be obtained using smoothed
ionospheric indices
[Liu et al., 1983;
Mikhailov et al., 1990b].
Further,
MF2 prediction accuracy improvement
can be achieved if
MF212 long-term prediction is established
using the McNish-Lincoln approach, but this requires access to
current ionospheric observations on the worldwide ionosonde
network.
A general way to derive a new set of
MF2 indices, say, for the current
period, requires observed monthly median
foF2 at many
northern hemispheric ionosonde stations, including equatorial and
high-latitude ones. Such an approach was applied to the 1957-1988
period, and so this set of
MF2 indices is considered the most
reliable. When the amount of ionosonde observations is not
sufficient for some reasons the other approach can be applied.
Using monthly median
foF2 observed over 10-20 representative
midlatitude ionosonde stations, local
MF2 indices can be obtained
via the
foF2 regression with
MF2 for these ionosondes; then the monthly
MF2 index
is calculated as an average over these local
MF2 indices.
One can get a monthly
MF2 index
by this way with pretty good
accuracy (mean relative deviation is about 3%). This approach was
used to derive
MF2 before 1957 and after 1988 (Table 1).
A comparable attempt to create a global ionospheric index (in megahertz)
was made by
Lal [1992].
Unfortunately, it is
difficult to evaluate its efficiency. But it should be noted that a
lot of approaches can be proposed for retrospective ionospheric
parameter variation description, but not all of them can be
efficiently used in practice for ionospheric long-term prediction.
The
M(3000)F2 regression analysis (Table 4) has shown that the
traditional sunspot number
R12 provides the best overall
accuracy compared with other ionospheric indices; only
MF2 turns out
to be a little bit better in some cases. This does not seem
surprising, as all considered ionospheric indices are based on
foF2 observations. On the other hand,
NmF2 and
hmF2 (which determines
M(3000)F2 ) depend in a different way on the same aeronomic
parameters
[Ivanov-Kholodny and Mikhailov, 1986].
For instance,
NmF2 is directly related to the EUV solar flux,
while
hmF2 reacts to the EUV changes indirectly via changes
in all thermospheric parameters. Further,
hmF2 is strongly controlled by
atmospheric temperature, while
NmF2 only slightly depends on
Tn.
During nighttime hours,
hmF2 variations
are mostly controlled by the
upward plasma drift resulting from thermospheric winds, while this
drift helps only to survive the nighttime
F2 region, preventing
NmF2 from rapid decay. There are some other differences.
So a special
ionospheric index should be designed for
M(3000)F2, but meanwhile
R12 may be recommended. In comparison with other
indices,
R12 seems to reflect better the overall level of
solar and geomagnetic
activity and hence atmospheric temperature, density, and winds
responsible for
hmF2 variations. The best efficiency of
R12 (Table 4) during high solar activity and equinox
periods, when
geomagnetic activity is enhanced, confirms this conclusion.
Conclusions
The main results of our consideration are summarized as follows:
1. The monthly improved ionospheric index
MF2 provides as good
a regression accuracy for
foF2 as other monthly ionospheric indices
IG,
IF2, and
T and much better accuracy in comparison with smoothed
12-month running mean
R12,
IG12,
IF212,
and
T12 indices
usually used for long-term ionospheric and HF radio communication
predictions. Distinct from direct solar indices, such effects as
"saturation" at high solar activity and "hysteresis"
foF2 in the
course of a solar cycle are avoided when
MF2 is used.
2. The monthly index
MF2 varies in a regular way with season in the
course of solar cycle similarly to the midlatitude monthly median
foF2. This opens the opportunity for its long-term
prediction. A
proposed method for
MF2 long-term prediction is based on the
MF2 relationship with
R12,
IG12,
IF212, or
MF212.
The accuracy of
MF2 derivation depends on the
solar cycle phase and equals 2-4% when observed
R12,
IG12,
IF212, or
MF212 indices are used. In a truly
prediction mode applied to solar cycle 21, the
MF2 prediction
accuracy was shown to be 4-6% if the
R12 long-term
(3-12 months in advance) forecast is used. The prediction accuracy can be
further improved using the
MF2 relationship with
MF212, but this
is possible on the basis of a prediction center where current
worldwide ionospheric observations are available.
3. Long-term (3-12 months in advance)
foF2 prediction for solar
cycle 21 has shown the advantage of the proposed approach over the
CCIR method based on the
R12 index. The
foF2 prediction accuracy is
improved by 36, 26 and 24% on average for 3, 6, and 12 months of lead
time, respectively. This is better than what may be obtained using
smoothed 12-month running mean ionospheric indices.
4. Different indices are required for
foF2 and
M(3000)F2 empirical
modeling and long-term prediction. This is due to the
different
dependence of
NmF2 and
hmF2 on main aeronomic parameters
responsible for the
F2 region formation. A special ionospheric
index should be designed for
M(3000)F2. Meanwhile,
MF2 for
foF2 and
R12 for
M(3000)F2 indices may be recommended for practical use.
References
Besprozvannaya, A. S., Longitudinal anomaly of the
F2 layer noon
ionization, Tr. AANII, 280, 100, 1966.
Bilitza, D. (Ed.), International Reference Ionosphere 1990, NSSDC 90-22,
Natl. Space Sci. Data Center, Greenbelt, Md., 1990.
Bradley, P. A., Indices of ionospheric response to solar-cycle
epoch,
Adv. Space Res., 13 (3), 25, 1993.
Caruana, J., The IPS monthly
T index,
in Solar-Terrestrial Predictions, Proceedings of a Workshop at Leura, Australia,
October 16-20, 1989, vol. 2, p. 257, 1990.
Chernyshov, O. V., and T. N. Vasil'eva, Prediction of Maximum Usable Frequency,
Nauka, Moscow, 1973.
International Radio Consultative Committee (CCIR),
Atlas of ionospheric characteristics, CCIR Rep. 340,
International Telecommunication Union,
Geneva, 1967-1990.
International Radio Consultative Committee (CCIR),
Choice of indices for long-term ionospheric prediction,
CCIR Recommendation 371,
International Telecommunication Union,
Geneva, 1990.
Ivanov-Kholodny, G. S., and A. V. Mikhailov,
The Prediction of Ionospheric Conditions, D Reidel, Norwell, Mass.,
1986.
Jones, W. B., and D. L. Obitts, Global representation of annual and
solar cycle variation of
foF2 monthly median 1954-1958,
Telecommun. Res. Rep. OT/ITS/RR3, U.S. Gov. Print. Off., Washington, D. C.,
1970.
Kouris, S. S., P. A. Bradley, and I. K. Nissopoulos, The
relationships of
foF2 and
M(3000)F2 versus
R12,
in COST 238/PRIME Workshop, pp. 155-168, Eindhoven, The Netherlands,
1994.
Lakshmi, D. R., B. M. Reddy, and R. S. Dabas, On the possible use
of recent EUV data for ionospheric predictions,
J. Atmos. Terr. Phys., 50, 207, 1988.
Lal, C., Global
F2 -layer ionization and geomagnetic activity,
J. Geophys. Res., 97, 12,153, 1992.
Liu, R. Y., P. A. Smith, and J. W. King, A new solar index which
leads to improved
foF2 predictions using the CCIR Atlas,
Telecommun. J., 50, 408, 1983.
McNish, A. G., and J. V. Lincoln, Prediction of sunspot numbers,
Trans. AGU, 30, 673, 1949.
Mikhailov, A. V., On the dependence of monthly median
foF2 on solar
activity indices, Adv. Space Res., 13 (3), 71, 1993.
Mikhailov, A. V., and V. V. Mikhailov, The hysteresis of critical
frequencies of the
F2 layer, Geomagn. Aeron., 33, 637, 1994.
Mikhailov, A. V., and V. V. Mikhailov, Solar cycle variations of
annual mean noon
foF2,
Adv. Space Res., 15 (2), 79, 1995a.
Mikhailov, A. V., and V. V. Mikhailov, A new ionospheric index
MF2,
Adv. Space Res., 15 (2), 93, 1995b.
Mikhailov, A. V., S. D. Buldenkova, V. V. Mikhailov, and Yu. L.
Teryokhin, A comparison of solar activity indices for the purposes
of modeling median values of
foF2,
Geomagn. Aeron., 30, 88, 1990a.
Mikhailov, A. V., Y. L. Teryokhin, and V. V. Mikhailov, Region
effective sunspot number for prediction of monthly median
F2 -layer critical frequencies, in Solar-Terrestrial Predictions,
Proceedings of a Workshop at Leura, Australia, October 16-20, 1989, vol. 2,
p. 341, 1990b.
Mikhailov, A. V., V. V. Mikhailov, and M. G. Skoblin, Monthly
median
foF2 and
M(3000)F2 ionospheric model over Europe,
Ann. Geofis., 39, 791, 1996.
Minnis, C. M., A new index of solar activity based on ionospheric
measurements, J. Atmos. Terr. Phys., 7, 310, 1955.
Minnis, C. M., and G. H. Bazzard, A monthly ionospheric index of
solar activity based on
F2 -layer ionization at eleven stations,
J. Atmos. Terr. Phys., 18, 297, 1960.
Rao, M. S. V. G., and R. S. Rao, The hysteresis variation in
F2 -layer parameters,
J. Atmos. Terr. Phys., 31, 1119, 1969.
Rothwell, P., Charged particles in the Earth's magnetic field and
the ionospheric
F2 -layer,
J. Phys. Soc. Jpn., 17, suppl. 1, 263,
1962.
Secan, J. A., and P. J. Wilkinson, Statistical studies of an
effective sunspot number, Radio Sci., 32, 1717, 1997.
Smith, P. A., and J. W. King, Long-term relationship between
sunspots, solar faculae and the ionosphere,
J. Atmos. Terr. Phys., 43, 1057, 1981.
Space Environment Center,
Prediction of smoothed sunspot number,
in Preliminary Reports and Forecast of Solar Geophysical Data, June 17, p. 3,
1997.
Turner, J. F., The development of the ionospheric index
T,
IPS Series R Report, R11,
Ionospheric Prediction Services, Darlingharst,
New South Wales, Australia, June 1968.
Turner, J. F., and P. J. Wilkinson, A weekly ionospheric index,
in
Solar-Terrestrial Predictions, Proceedings of Workshop at Boulder, Co., USA,
April 23-27, 1979, vol. 1,
pp. 279-287, 1979.
Wilkinson, P. J., Daily indices,
in
Solar-Terrestrial Predictions, Proceedings of Workshop at Meudon, France, June
18-22, 1984, pp. 505-508, 1986a.
Wilkinson, P. J., Monthly ionospheric indices,
in
Solar-Terrestrial Predictions, Proceedings of Workshop at Meudon, France, June
18-22, 1984, pp. 496-499, 1986b.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.2.0) on November 4, 1998.
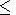 100 nm
as an
index for
foF2 regression, turned out to be not very efficient
[Mikhailov et al., 1990a].
A similar conclusion follows from
analysis of results obtained by
Lakshmi et al. [1988],
where the dependence of
foF2 versus the measured solar flux in
the
l= 17-19 nm interval was used. Such results
are not surprising,
as
solar EUV radiation reflects only one side of the
F2 region
formation, namely,photoionization. From this point of view, the
traditional 12-month running mean sunspot number
R12 seems to be
more preferable than other direct solar indices as it serves
implicitly as an indicator not only of ionization efficiency, but
of the overall state of the upper atmosphere. On the other hand, it
should be kept in mind that the
foF2 versus
R12 regression
accuracy can be improved using a nonlinear dependence instead of
a linear one
[Jones and Obitts, 1970;
Mikhailov, 1993],
and so
R12 can be efficiently used in practice.
100 nm
as an
index for
foF2 regression, turned out to be not very efficient
[Mikhailov et al., 1990a].
A similar conclusion follows from
analysis of results obtained by
Lakshmi et al. [1988],
where the dependence of
foF2 versus the measured solar flux in
the
l= 17-19 nm interval was used. Such results
are not surprising,
as
solar EUV radiation reflects only one side of the
F2 region
formation, namely,photoionization. From this point of view, the
traditional 12-month running mean sunspot number
R12 seems to be
more preferable than other direct solar indices as it serves
implicitly as an indicator not only of ionization efficiency, but
of the overall state of the upper atmosphere. On the other hand, it
should be kept in mind that the
foF2 versus
R12 regression
accuracy can be improved using a nonlinear dependence instead of
a linear one
[Jones and Obitts, 1970;
Mikhailov, 1993],
and so
R12 can be efficiently used in practice.

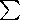 D2 - (
D2 - (