k according to the dispersion relation
(in our case, equation (5)). Since the quantities
k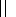 and
k
and
k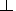 which enter (5)
are expressed through Cartesian coordinates and wave vector components
in a rather complicated way, the Cartesian variables are not the proper ones
for our problem.
That is why we will use dipolar coordinates
L, M, connected with Cartesian coordinates
(x, z) by the relations
which enter (5)
are expressed through Cartesian coordinates and wave vector components
in a rather complicated way, the Cartesian variables are not the proper ones
for our problem.
That is why we will use dipolar coordinates
L, M, connected with Cartesian coordinates
(x, z) by the relations
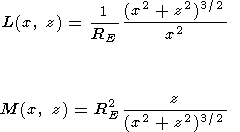 | (8) |
Here
RE is the Earth's radius; the origin of the Cartesian
coordinates is supposed to be at the Earth's center, the
z axis
pointing along the dipolar axis from S to N.
The coordinate
L is
McIlwain's parameter, which is constant along the field line; the coordinate
M is measured along the field line from the equator
(see Figure 2).
The Lamé
coefficients corresponding to the coordinates
L, M are
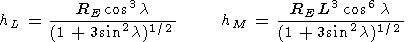 | (9) |
where
l is the geomagnetic latitude:
tan l = z/x.
The momenta
PL, PM canonically conjugate
to the coordinates
L, M are related to the transverse and longitudinal wave vector
components
k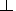 , k
, k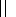 by
by
 | (10) |
In new variables
(L, M, PL, PM), the
expression
for the wave frequency (5) playing the role of the
Hamiltonian from which the equations of geometrical optics
can be derived takes the form
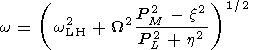 | (11) |
where the following notation has been introduced
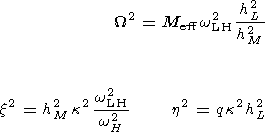 | (12) |
and it is supposed that the quantities
wLH, W,
x, and
h are expressed as the
functions of coordinates
L, M.
Using (4) and notation (12) and taking into account
(wLH2 /wH2)
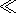 1,
we obtain the relations between different
quantities entering (11):
1,
we obtain the relations between different
quantities entering (11):
 | (13) |
We now write the equations of geometrical optics which follow from
(11):
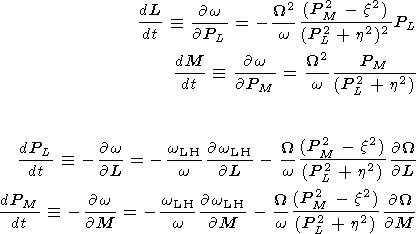 | (14) |
While deriving equations (14) for momenta
PL and
PM,
we have made use of
the fact that, under conditions (13),
the derivatives of the
quantities
x2 and
h2 can be neglected.
The physical meaning of the derivatives
dL/dt and
dM/dt is revealed by the relations which connect
these quantities with transversal and longitudinal components
of the group velocity. Since
hL dL is equal to the
length across the geomagnetic field line corresponding to
the variation
dL of the coordinate
L at constant
M and
hM dM is the length along the field line
corresponding to the variation
dM at constant
L,
then
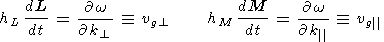 | (15) |
which, of course, is equivalent to the first two equations
in (14) in view of the relations (10).
We proceed with the analysis of the wave propagation near the LHR
frequency by comparing the longitudinal and transversal group
velocities (15).
From (14) it follows that the ratio
between these two quantities depends on the magnitude of the
longitudinal momentum
PM.
We will relate the value of
PM2 to the quantity
x2, keeping in mind that
in view of limitations (13) the
relation between
PM2 and
x2 may be arbitrary.
We divide the range of
the permitted values of the quantity
PM2 into two domains:
PM2 x2
and
PM2 < x2.
From (13) and (14) it is easy to see that
for
PM2 x2,
|hMdM/dt| 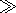 |hLdL/dt| ; thus the wave
group velocity is almost aligned with the ambient magnetic field.
For
PM2 < x2,
| vg
|hLdL/dt| ; thus the wave
group velocity is almost aligned with the ambient magnetic field.
For
PM2 < x2,
| vg 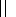 | is still
larger than
| vg
| is still
larger than
| vg 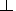 | unless
PM2 is as small as
| unless
PM2 is as small as
 hL2 x4/hM2
PL2, and for smaller
PM2, | vg
hL2 x4/hM2
PL2, and for smaller
PM2, | vg 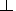 | > | vg
| > | vg 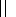 |.
Thus on the greater part of the wave trajectory,
| vg
|.
Thus on the greater part of the wave trajectory,
| vg 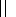 | is larger
than
|vg
| is larger
than
|vg 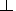 |, which permits,
in some cases,
the reduction of
the problem to a one-dimensional one. This has been done in the papers by
Bosková et al. [1988,
1992].
On this basis, the explanation of the lower hybrid
resonance whistler traces has been attacked.
However, for the problem discussed here,
such an approach is not pertinent.
Thus in this study, we will abandon the limitation
of one-dimensional wave propagation.
|, which permits,
in some cases,
the reduction of
the problem to a one-dimensional one. This has been done in the papers by
Bosková et al. [1988,
1992].
On this basis, the explanation of the lower hybrid
resonance whistler traces has been attacked.
However, for the problem discussed here,
such an approach is not pertinent.
Thus in this study, we will abandon the limitation
of one-dimensional wave propagation.
It follows from (14) that the sign of
vg 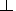 depends on the sign
of
PL ; namely, they have the opposite signs for
(PM2 - x2)
> 0 and the same signs for
(PM2 - x2)
< 0.
As was shown by ray tracing calculations
[Walter and Angerami, 1969],
the wave
normal vector of the nonducted whistler wave turns antiearthward while
propagating in the magnetosphere (for realistic models of plasma
distribution). Thus the wave reaches the outer ionosphere after
propagating from one hemisphere to another with
PL > 0 (see (10)).
For these waves, which we consider later on,
vg
depends on the sign
of
PL ; namely, they have the opposite signs for
(PM2 - x2)
> 0 and the same signs for
(PM2 - x2)
< 0.
As was shown by ray tracing calculations
[Walter and Angerami, 1969],
the wave
normal vector of the nonducted whistler wave turns antiearthward while
propagating in the magnetosphere (for realistic models of plasma
distribution). Thus the wave reaches the outer ionosphere after
propagating from one hemisphere to another with
PL > 0 (see (10)).
For these waves, which we consider later on,
vg 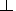 < 0 on the greater
part of a trajectory,
so that the wave moves predominantly toward
lower
L shells. As for
vg
< 0 on the greater
part of a trajectory,
so that the wave moves predominantly toward
lower
L shells. As for
vg 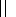 ,
it has the same sign as
PM, and both change sign
at the wave reflection point (over the longitudinal
coordinate
M ).
,
it has the same sign as
PM, and both change sign
at the wave reflection point (over the longitudinal
coordinate
M ).
3. The Mechanism of Wave Trapping in the Waveguide
No matter that the wave group velocity is almost aligned with
the ambient magnetic field, even slow motion of the wave across
the field lines is essential to our problem. Thus we shall
consider a two-dimensional problem, although the
dependence of the quantities upon the coordinate
L may be
considered as a slow dependence on the time scale of the wave longitudinal
motion.
We now rewrite the equations (14) in the form
 | (16) |
where
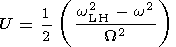 | (17) |
The qualitative physical mechanism of the wave trapping
into the waveguide can be understood from the well-known
analogy between geometrical optics and mechanics
[Fermi,1968],
where mass point corresponds to the
wave packet, and particle trajectory corresponds to the
ray path. Equations (16)
for
M and
PM resemble the
equations of particle motion in the potentional of the kind (17)
which has a maximum and a minimum over the
M coordinate,
corresponding to the maximum and minimum of the LHR frequency
profile, and a potential wall, corresponding to the bottom part
of the profile (see Figure 1).
Since the problem is two dimensional, the effective potential
also
depends
on the coordinate
L as a parameter.
Once passing near the potential maximum, the
particle continues to move over both
M and
L coordinates. Then if the
potential maximum increases, the particle can be trapped after
reflection from the potential wall. A monotonic increase
of the potential maximum, connected with a monotonic variation
of the LHR maximum with
L coordinate, guarantees
that the particle will stay in the trap and, correspondingly,
the wave will remain in the waveguide.
For a precise description of the wave trapping,
a more strict consideration is needed.
Toward this direction, we proceed in the following way.
Since the Hamiltonian (11)
is independent of time and, thus, is a constant of motion,
the problem can be reduced to a
one-dimensional one in a standard way
(see, for example,
Arnold [1974]).
We suppose the quantity
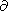 U /
U / 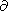 L to be sign determined
and choose
PL as a new independent variable.
Dividing the equations (14) for
M, and
PM by
(dPL/dt) and excluding the quantity
L with the help of the integral (11),
we arrive at two equations for the variables
M and
PM as functions of
PL. These equations are derived from the Hamiltonian
H = L(M, PM; PL,
w), which
(up to arbitrary constant) is nothing but
the coordinate
L expressed from (11)
as a function of
M, PM; PL, and parameter
w.
To find the function
L(M, PM; PL, w),
we rewrite the relation (11) in the form
L to be sign determined
and choose
PL as a new independent variable.
Dividing the equations (14) for
M, and
PM by
(dPL/dt) and excluding the quantity
L with the help of the integral (11),
we arrive at two equations for the variables
M and
PM as functions of
PL. These equations are derived from the Hamiltonian
H = L(M, PM; PL,
w), which
(up to arbitrary constant) is nothing but
the coordinate
L expressed from (11)
as a function of
M, PM; PL, and parameter
w.
To find the function
L(M, PM; PL, w),
we rewrite the relation (11) in the form
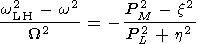 | (18) |
For the sake of simplicity, we neglect the dependence of the
quantities
x2 and
h2 on coordinate
L.
As was shown above, the variation of coordinate
L is small; thus we may expand the
expression on the left-hand side in (18)
around initial coordinate
L0. It is
convenient to write this expansion in the form
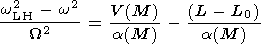 | (19) |
Putting this expansion into (18),
we find the quantity
(L - L0) which plays
the role of the Hamiltonian in the problem
 | (20) |
In our case, the role of independent variable is played
by the quantity
PL, whereas the usual independent
variable in the equations of motion is time. To restore
the habitual notation, we denote
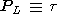 | (21) |
The Hamiltonian (20) depends on
t and, thus, varies along the wave trajectory.
At the same time,
according to the definition of
H as
L - L0,
its initial value at
L = L0 is equal to zero.
We proceed with the analysis of the equations
derived from (20), keeping in mind that the equations
of geometrical optics describe the wave propagation
in real space with a group velocity, the role of momentum being
played by a wave vector. Positive direction of the
M axis in the northern hemisphere
is from the equator to the Earth
(see Figure 2),
so that increasing
M values correspond to decreasing heights.
We will consider waves having positive
PM above the LHR maximum
and, thus, propagating to the Earth.
 To get an idea about the shape of potential
V(M), we notice
that according to (19)
To get an idea about the shape of potential
V(M), we notice
that according to (19)
 | (22) |
It is natural to assume that
a(M)/W2
is a slowly varying
(as compared to
wLH2 ), sign-determined
function.
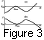
Thus roughly speaking, the shape of potential
V(M), up to
the sign of
a(M), is similar to the shape
of the LHR frequency profile. The qualitative shape of the potential
V(M) is schematically illustrated
in Figure 3a
and Figure 3b
for
a > 0 and
a< 0, respectively. We should mention that
a > 0 corresponds to an increase of LHR frequency
with decreasing
L shell, and vice versa.
We can now give a simple, but strict, interpretation of the
wave trapping into the wave-guide.
The equations for
M, PM as functions of
the independent variable
t which follow from
(20) have the form
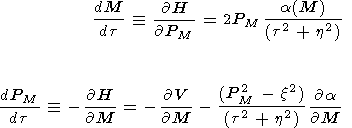 | (23) |
At the same time, the Hamiltonian (20) itself
varies with
t according to the equation
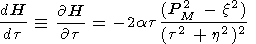 | (24) |
Let us first consider the case
a > 0,
when the potential
V(M) has the shape
represented in Figure 3a.
Using the definitions of the quantities
V (equation (22)) and
x2 (equation (12)) and inequalities
(13), one can
easily show that
DV  V(M)
V(M)
 ax2/(t2 + h2),
where
DV is the variation of potential across
the LHR profile.
From (20) it then follows that the wave cannot penetrate deeply
under the potential wall. At point
Mmax, corresponding
to the maximum of the potential
V(M), let the quantity
H (equation (20))
be larger, but close to
Vmax.
(We remind the reader that
initially
H = 0,
while
Vmax
ax2/(t2 + h2),
where
DV is the variation of potential across
the LHR profile.
From (20) it then follows that the wave cannot penetrate deeply
under the potential wall. At point
Mmax, corresponding
to the maximum of the potential
V(M), let the quantity
H (equation (20))
be larger, but close to
Vmax.
(We remind the reader that
initially
H = 0,
while
Vmax  (wLH2
- w2)max,
so that such a situation appears when
w (wLH)max.)
In this case the wave passes over the potential maximum. Then the
quantity
H varies according to (24), and as was shown
above, for
a > 0 it decreases over the greater part of the
profile. Thus the wave becomes trapped between the potential wall
and the potential maximum.
In this consideration we assumed
t
(wLH2
- w2)max,
so that such a situation appears when
w (wLH)max.)
In this case the wave passes over the potential maximum. Then the
quantity
H varies according to (24), and as was shown
above, for
a > 0 it decreases over the greater part of the
profile. Thus the wave becomes trapped between the potential wall
and the potential maximum.
In this consideration we assumed
t PL
>0,
in agreement with general properties of nonducted
whistler wave propagation (see the end of section 2).
PL
>0,
in agreement with general properties of nonducted
whistler wave propagation (see the end of section 2).
Let us turn to the case
a< 0.
One should now be cautious in using a
similarity with particle motion in a potential, since
the case
a< 0 formally corresponds to
the motion of a particle with negative mass.
As before, the initial value of the
Hamiltonian
H (equation (20)) is equal to zero,
while the shape of potential
V (Figure 3b)
is reversed
as compared with the case
a > 0. Using similar arguments
as above, one can show that in the
case
a< 0, the wave cannot penetrate far above
the potential minimum
Vmin,
while trapped waves correspond to
H > Vmin.
Since initially
H < Vmin,
for a wave to be trapped, an increase of the quantity
H along the wave trajectory would be necessary. However, it is not the case
when
a< 0. Indeed, from (16) and (22)
it follows that for
a< 0, dPL/dt  dt/dt
< 0, so that the value of
t decreases along the wave path.
Equation (24) then shows that
during the time of wave crossing of the LHR profile,
the quantity
H decreases on the whole.
Thus the wave cannot be trapped in the waveguide
in the case
a< 0, that is, when the LHR
frequency decreases with a decrease of
L shell. We should stress that,
independently of the sign of
a,
the quantity
PL
dt/dt
< 0, so that the value of
t decreases along the wave path.
Equation (24) then shows that
during the time of wave crossing of the LHR profile,
the quantity
H decreases on the whole.
Thus the wave cannot be trapped in the waveguide
in the case
a< 0, that is, when the LHR
frequency decreases with a decrease of
L shell. We should stress that,
independently of the sign of
a,
the quantity
PL  t
is large
(as compared with
PM and
h )
and positive and that, on the average,
PM2
t
is large
(as compared with
PM and
h )
and positive and that, on the average,
PM2  x2.
These facts have been assumed in the analysis of trapping
conditions.
x2.
These facts have been assumed in the analysis of trapping
conditions.
To summarize, the possibility for LHR waveguide
feeding by nonducted VLF waves propagating
in the magnetosphere appears when the two-dimensional
LHR frequency profile satisfies the following requirements:
the profile of the LHR frequency along a given geomagnetic field line
(i.e., the line
L = const) has
a valley lying between local maximum, local minimum, and
the bottom wall, and the value of local maximum along
the field line increases with decreasing
L shells.
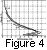 Figure 4 shows model LHR frequency profiles which satisfy
these requirements. The LHR frequency (horizontal axis)
is plotted as a function of height from the
Earth (vertical axis) along the geomagnetic field lines
L = 2, 3, and
4. Similar to Figure 1,
the lower ionospheric heights are not shown in Figure 4.
Figure 4 shows model LHR frequency profiles which satisfy
these requirements. The LHR frequency (horizontal axis)
is plotted as a function of height from the
Earth (vertical axis) along the geomagnetic field lines
L = 2, 3, and
4. Similar to Figure 1,
the lower ionospheric heights are not shown in Figure 4.
 Examples of wave trajectories corresponding to wave trapping
in the LHR waveguide, obtained from the ray tracing calculations
using the profiles of Figure 4, are shown in Figure 5.
We should emphasize that they are model ray tracing calculations,
since they use analytical LHR profiles shown in
Figure 4
that resemble the calculated profile in Figure 1
and they satisfy the above formulated conditions for the wave
trapping. Figure 5a
shows the ray paths in Cartesian coordinates
(x, z) where the trapping is manifested as line
broadenings in the near-Earth region; Figure 5b displays
the same wave trajectories in
(L, M) coordinates
where the wave trapping is most evident. When the wave becomes
trapped in the LHR waveguide, the longitudinal coordinate
M of the wave trajectory starts oscillating, while the transversal
coordinate
L decreases on the average, in agreement
with the analytical results of section 3.
We should stress that the quasi-resonant mode of propagation
and proper features of LHR profiles do not guarantee wave trapping:
the wave may well be reflected either above
hmax or even from the bottom of the profile, but still
leave the waveguide. For a wave to be trapped, it should have
a frequency sufficiently close to the local maximum
of the LHR frequency along the wave path.
That is why the wave may be trapped after one or several
hops in the magnetosphere, when appropriate conditions
for trapping arise.
Examples of wave trajectories corresponding to wave trapping
in the LHR waveguide, obtained from the ray tracing calculations
using the profiles of Figure 4, are shown in Figure 5.
We should emphasize that they are model ray tracing calculations,
since they use analytical LHR profiles shown in
Figure 4
that resemble the calculated profile in Figure 1
and they satisfy the above formulated conditions for the wave
trapping. Figure 5a
shows the ray paths in Cartesian coordinates
(x, z) where the trapping is manifested as line
broadenings in the near-Earth region; Figure 5b displays
the same wave trajectories in
(L, M) coordinates
where the wave trapping is most evident. When the wave becomes
trapped in the LHR waveguide, the longitudinal coordinate
M of the wave trajectory starts oscillating, while the transversal
coordinate
L decreases on the average, in agreement
with the analytical results of section 3.
We should stress that the quasi-resonant mode of propagation
and proper features of LHR profiles do not guarantee wave trapping:
the wave may well be reflected either above
hmax or even from the bottom of the profile, but still
leave the waveguide. For a wave to be trapped, it should have
a frequency sufficiently close to the local maximum
of the LHR frequency along the wave path.
That is why the wave may be trapped after one or several
hops in the magnetosphere, when appropriate conditions
for trapping arise.
The trajectory marked "1 hop trapping" gives an example
of wave trapping in the LHR waveguide after one hop between
conjugate hemispheres. The wave propagates in the
magnetosphere in a nonducted mode, enters a quasi-resonant regime
of propagation, and crosses the LHR maximum in the opposite hemisphere having
a frequency slightly higher than
(wLH)max.
While the wave continues moving toward the bottom of the profile,
at the same time it shifts to lower
L shells
at which the LHR maximum increases. After reflection from the bottom
of the profile, the wave approaches the maximum of the LHR profile with
w< (wLH)max
at which quasi-resonant waves cannot propagate. The wave is reflected
from the LHR maximum and, thus, becomes trapped in the waveguide.
The trajectories marked "2 hop trapping" and
"3 hop trapping" give examples of more complicated
trajectories where the trapping takes place after two
and three hops in the magnetosphere. The case of a two hop trapping
has been found by
B. V. Lundin (private communication, 1998)
in ray tracing calculations
using the model of diffusive equilibrium
[Angerami and Thomas, 1964]
for evaluation
of LHR profiles. These rather specific wave trajectories
shown in Figure 5
become clear in view of the present study.
4. Comparison With Experimental Data
In this section we discuss the experimental results which show
the possibility of LHR waveguide feeding by the mechanism
suggested above. Since satellite measurements are always local in
space, some evidence of the fact that a satellite is inside the
wave-guide should be provided. In fact, for a more profound discussion of
the wave trapping, we need simultaneous measurements of the
electromagnetic field in a wide band and cold plasma parameters,
namely, ion content and temperature. Such complex data were
available from the measurements performed on board the Intercosmos 24
satellite
[Bosková et al.,1993].
To give a reference in light of which the waveguide
feeding could be discussed, it is convenient to consider it
together with other well-known phenomena, the so-called LHR
whistlers
[Bosková et al., 1992;
Charcosset et al.,1973;
Morgan et al.,1977].
That is why we discuss here the same experimental
data which have previously been used in the study of LHR whistlers
[Bosková et al., 1992].
It is all the more reasonable since, according to the
results of
Bosková et al.[1992],
which we will use in the following discussion,
LHR whistlers should be observed just inside the LHR waveguide.
 An example of a spectrogram in the 10-kHz
frequency band is shown in the upper panel of Figure 6.
The spectrogram is obtained
from electric field measurements and is most appropriate for
discussing quasi-electrostatic wave phenomena. During the time
interval shown in the figure, the satellite height was about 600 km,
while the McIlwain parameter increased from
L = 2.2 to
L = 2.4. The
main VLF wave phenomena seen in the picture are as follows:
usual ducted
whistlers whose traces expand in the whole frequency band; LHR
whistlers seen in the upper part of the panel, which have a clear
cutoff frequency; and pronounced noise close to the local LHR
frequency. The lower cutoff frequency of LHR whistlers
gives a good estimation of
the maximum LHR frequency above the satellite. This frequency is
shown by the dashed line in the lower panel of Figure 6,
while the solid line shows the local
LHR frequency along the satellite path calculated from the
measurements of cyclotron frequency and ion composition.
An example of a spectrogram in the 10-kHz
frequency band is shown in the upper panel of Figure 6.
The spectrogram is obtained
from electric field measurements and is most appropriate for
discussing quasi-electrostatic wave phenomena. During the time
interval shown in the figure, the satellite height was about 600 km,
while the McIlwain parameter increased from
L = 2.2 to
L = 2.4. The
main VLF wave phenomena seen in the picture are as follows:
usual ducted
whistlers whose traces expand in the whole frequency band; LHR
whistlers seen in the upper part of the panel, which have a clear
cutoff frequency; and pronounced noise close to the local LHR
frequency. The lower cutoff frequency of LHR whistlers
gives a good estimation of
the maximum LHR frequency above the satellite. This frequency is
shown by the dashed line in the lower panel of Figure 6,
while the solid line shows the local
LHR frequency along the satellite path calculated from the
measurements of cyclotron frequency and ion composition.
The LHR frequency profile shown in Figure 1
corresponds to the point
denoted by arrows in Figure 6. That profile has been calculated
with the help of the diffusive equilibrium model
[Angerami and Thomas, 1964],
with the use of ion density
and temperature measurements at satellite altitudes.
Four ions (H
+, He
+, O
+, N
+ )
have been included in the model,
and a temperature
gradient of
0.6o K km
-1 has been used.
The maximum frequency in the LHR
profile shown by the bold dot in
the lower panel of Figure 6 is quite close to the LHR
whistler cutoff frequency, in agreement with the theory developed
in the paper by
Bosková et al. [1992].
From the satellite position shown in Figure 1 we see that
during this time the satellite was inside the waveguide.
As we believe that the LHR whistler cutoff frequency is close
to the maximum frequency in the LHR profile, the noise
band below that frequency clearly seen
on the spectrogram in Figure 6 indicates that the LHR
waveguide is fed by quasi-electrostatic waves. The fact that the noise
band is more pronounced in the lower part of the waveguide
frequency band is quite consistent with the mechanism of the
waveguide feeding discussed in section 3. Indeed,
these waves should mostly have been trapped early. Since the
parameter
k2c2/wp2
increases
while the wave propagates in the duct,
it becomes more electrostatic and, thus, more intense.
We should point out that in the same frequency band
that corresponds to the frequencies in the waveguide,
the parts of usual whistler traces are stressed,
which are weaker (or not seen at all) out of that band.
In conclusion, in this paper we have theoretically studied
the LHR waveguide feeding by quasi-resonant VLF waves
propagating in the magnetosphere in a nonducted mode.
The analysis of wave trapping is performed in the
framework of two-dimensional geometrical optics.
It is shown that the trapping of downward propagating
quasi-resonant whistler mode waves into the LHR waveguide
takes place when the values of local maxima of LHR frequencies
along geomagnetic field lines increase with decreasing
L shells.
Analytical consideration is illustrated and supplemented
by model ray tracing calculations. The theoretical model is tested against
experimental data, and qualitative consistency is found.
Acknowledgments
D. R. Shklyar
wishes to thank the Ionospheric Department of the
Institute of Atmospheric Physics in Prague for its hospitality
and financial support during his visits there when this study
was conducted.
Useful discussions with B. V. Lundin are also acknowledged.
This work was supported by RFFR grant 96-02-19225a.
References
Angerami, J. J., and J. O. Thomas,
Studies of planetary atmospheres, 1, The distribution of electrons and ions
in the Earth's exosphere, J. Geophys. Res., 69,4537, 1964.
Arnold, V. I., Mathematical Methods in Classical Mechanics,
Nauka,
Moscow, 1974.
Bell, T. F., and H. D. Ngo, Electrostatic lower hybrid waves
excited by electromagnetic whistler mode waves scattering from
planar magnetic-field-aligned plasma density irregularities,
J. Geophys. Res., 95,149, 1990.
Bosková, J., F. Jirícek,
O. A. Mal'tseva, E. E. Titova, P. Tríska,
and
D. R. Shklyar, On the nature of lower-hybrid whistlers,
Geomagn. Aeron. 28,912, 1988.
Bosková, J., F. Jirícek, J. Smilauer,
P. Tríska, B. V. Lundin, D. R. Shklyar,
and E. E. Titova,
LHR whistlers and LHR spherics in the outer ionosphere,
J. Atmos. Terr. Phys., 54,1321, 1992.
Bosková, J., F. Jirícek, J. Smilauer,
P. Tríska, V. V. Afonin, and V. G. Istomin,
Plasmaspheric refilling phenomena observed by the Intercosmos 24 satellite,
J. Atmos. Terr. Phys., 55,1595, 1993.
Brice, N. M., and R. L. Smith,
Lower hybrid resonance emissions,
J. Geophys. Res., 70,71, 1965.
Charcosset, G., M. Tixier, Y. Corcuff, and M. Garnier,
Étude expérimental
et théorique
de sifflements non guidés recus aus basses
latitudes
bord du satellite Alouette 2,
Ann. Geophys., 29,279, 1973.
Fermi, E.,
Notes on Quantum Mechanics,
Mir,
Moscow,
1968.
Helliwell, R. A., Whistlers and Related Ionospheric Phenomena,Stanford Univ.
Press, Stanford, Calif., 1965.
Horita, R. E.,
Wave-particle interaction around the lower hybrid resonance,
Planet. Space Sci., 20,409, 1972.
Horita, R. E., and T. Watanabe,
Electrostatic waves in the ionosphere excited around
the lower hybrid resonance frequency,
Planet. Space Sci., 17,61, 1969.
Jirícek, F., and P. Tríska,
LHR-associated phenomena observed with the Intercosmos 10 satellite,
Space Res., XVI, 567,
Berlin,
1976.
Kimura, I., Whistler mode propagation in the Earth
and planetary magnetospheres and ray tracing techniques,
Space Sci. Rev., 42,449, 1985.
Laaspere, T., and H. A. Taylor, Jr.,
Comparison of certain VLF noise phenomena with the
lower hybrid resonance frequency calculated from
simultaneous ion composition measurements,
J. Geophys. Res., 75, 97, 1970.
Morgan, M. G., P. E. Brown, W. C. Johnson,
and H. A. Taylor, Jr.,
An improved comparison of the LHR frequency observed
by a VLF receiver and calculated from ion density measurements
on the same spacecraft,
Radio Sci., 12, 811, 1977.
Nishino, M., and Y. Tanaka,
Observations of auroral LHR noise by the sounding rocket S-310JA-6,
Planet. Space Sci., 35,127, 1969.
Ratcliffe, J. A.,
The Magneto-Ionic Theory and Its Applications to the Ionosphere,Cambridge
Univ. Press, New York, 1959.
Shklyar, D. R., and H. Washimi, LHR wave excitation by whistlers in
the magnetospheric plasma, J. Geophys. Res., 99,23,695, 1994.
Smith, R. L., I. Kimura, J. Vineron, and J. Katsufrakis,
Lower hybrid resonance noise and a new ionospheric duct,
J. Geophys. Res., 71,1925, 1966.
Stix, T. H.,
Theory of Plasma Waves,McGraw-Hill New York, 1962.
Trakhtengerts, V. Yu., and M. Hayakawa,
A wave-wave interaction in whistler frequency range in space plasma,
J. Geophys. Res., 98,19,205, 1993.
Walter, F., and J. J. Angerami,
Nonducted mode of VLF propagation between conjugate hemispheres:
Observations on OGO 2 and 4 of the "walking-trace" whistler and of
Doppler shifts in fixed frequency transmissions,
J. Geophys. Res., 74,6352, 1969.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.2.0) on August 13, 1999.
 Although wave propagation inside the waveguide was considered
in many papers beginning with the pioneering work
by
Smith et al.[1966],
the mechanism of
the waveguide feeding remained unclear. That question is
dealt with in this paper. To formulate the problem
in more detail, we recall the well-known features
of quasi-resonant LHR waves
[Stix, 1962]:
large (close to
p/2 ) wave normal angle
q with respect to an ambient magnetic field
B0 ;
short wavelength corresponding
to large refractive index (more precisely,
k2 c2/wp2
Although wave propagation inside the waveguide was considered
in many papers beginning with the pioneering work
by
Smith et al.[1966],
the mechanism of
the waveguide feeding remained unclear. That question is
dealt with in this paper. To formulate the problem
in more detail, we recall the well-known features
of quasi-resonant LHR waves
[Stix, 1962]:
large (close to
p/2 ) wave normal angle
q with respect to an ambient magnetic field
B0 ;
short wavelength corresponding
to large refractive index (more precisely,
k2 c2/wp2
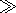 1,
where
k is the wave number,
wp is electron plasma frequency,
and
c is
the speed of light); and the quasi-electrostatic character
of the wave field.
Such a wave cannot propagate in the region where
its frequency
w is essentially smaller than the
local LHR frequency
wLH (see dispersion
equation (5) and relation (7) below).
A typical LHR frequency profile in the outer ionosphere
is shown in Figure 1.
According to the
tradition of representing this profile, the
altitude is along the vertical axis,
while the frequency
wLH is along the horizontal one.
In the plane
( wLH, altitude),
the wave trajectory corresponds to a vertical line
w = const.
If the wave moves towards increasing values
of
wLH, its group velocity decreases,
and the wave is reflected in the vicinity of the point
where this line crosses the LHR frequency profile.
Thus waves with frequencies
(wLH)min < w<
(wLH)max, if they exist in
the waveguide
(that is, below
hmax ), would
be trapped inside the waveguide. But, at first sight, the waveguide
could not be fed either from above or from below, and the
quasi-resonant LHR waves described above
should be excited directly inside the waveguide.
As was mentioned above, the corresponding mechanisms
of local excitation of LHR waves were suggested,
namely, scattering of upgoing waves
on small-scale turbulence or plasma stream instability.
However, these local mechanisms require some additional
conditions to be fulfilled in the waveguide region, namely,
the existence of small-scale plasma turbulence or density
irregularities in the case of wave scattering or the existence
of energetic electron streams in the case of instability.
At the same time, the most natural way of waveguide feeding
would be wave penetration from higher altitudes,
where quasi-resonant VLF waves propagating in a nonducted mode
normally exist. In this paper we suggest
a mechanism of LHR waveguide feeding by those waves
and give evidence for this mechanism derived from
ray tracing calculations and satellite observations.
The analysis is based on the solution of the equations
of geometrical optics, with the account of a realistic
two-dimensional shape of the LHR frequency profile.
We should emphasize underline that we consider wave propagation
only in the upper ionosphere and the magnetosphere, while
wave propagation in the lower ionosphere, where the
LHR frequency essentially decreases owing to exhaustion
of the ionized plasma component, is beyond the scope of the present
work. Accordingly, in Figure 1 and Figure 4 below,
we do not show LHR profiles in this region of the lower
ionosphere (heights
h 100-200 km).
1,
where
k is the wave number,
wp is electron plasma frequency,
and
c is
the speed of light); and the quasi-electrostatic character
of the wave field.
Such a wave cannot propagate in the region where
its frequency
w is essentially smaller than the
local LHR frequency
wLH (see dispersion
equation (5) and relation (7) below).
A typical LHR frequency profile in the outer ionosphere
is shown in Figure 1.
According to the
tradition of representing this profile, the
altitude is along the vertical axis,
while the frequency
wLH is along the horizontal one.
In the plane
( wLH, altitude),
the wave trajectory corresponds to a vertical line
w = const.
If the wave moves towards increasing values
of
wLH, its group velocity decreases,
and the wave is reflected in the vicinity of the point
where this line crosses the LHR frequency profile.
Thus waves with frequencies
(wLH)min < w<
(wLH)max, if they exist in
the waveguide
(that is, below
hmax ), would
be trapped inside the waveguide. But, at first sight, the waveguide
could not be fed either from above or from below, and the
quasi-resonant LHR waves described above
should be excited directly inside the waveguide.
As was mentioned above, the corresponding mechanisms
of local excitation of LHR waves were suggested,
namely, scattering of upgoing waves
on small-scale turbulence or plasma stream instability.
However, these local mechanisms require some additional
conditions to be fulfilled in the waveguide region, namely,
the existence of small-scale plasma turbulence or density
irregularities in the case of wave scattering or the existence
of energetic electron streams in the case of instability.
At the same time, the most natural way of waveguide feeding
would be wave penetration from higher altitudes,
where quasi-resonant VLF waves propagating in a nonducted mode
normally exist. In this paper we suggest
a mechanism of LHR waveguide feeding by those waves
and give evidence for this mechanism derived from
ray tracing calculations and satellite observations.
The analysis is based on the solution of the equations
of geometrical optics, with the account of a realistic
two-dimensional shape of the LHR frequency profile.
We should emphasize underline that we consider wave propagation
only in the upper ionosphere and the magnetosphere, while
wave propagation in the lower ionosphere, where the
LHR frequency essentially decreases owing to exhaustion
of the ionized plasma component, is beyond the scope of the present
work. Accordingly, in Figure 1 and Figure 4 below,
we do not show LHR profiles in this region of the lower
ionosphere (heights
h 100-200 km).
 w
w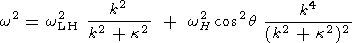
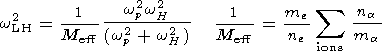
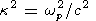
 wp/c.
For the so-called
quasi-longitudinal waves
[Ratcliffe,
wp/c.
For the so-called
quasi-longitudinal waves
[Ratcliffe,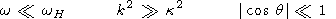

 and
k
and
k are the longitudinal
and transversal components of the
wave vector, respectively,
and
are the longitudinal
and transversal components of the
wave vector, respectively,
and

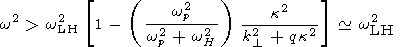

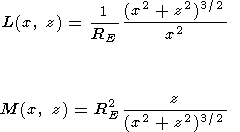
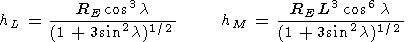

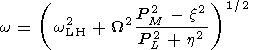
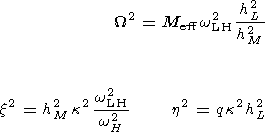

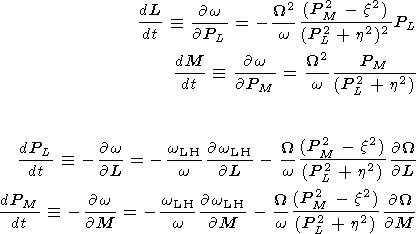
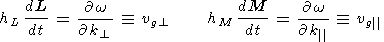
 hL2 x4/hM2
PL2, and for smaller
PM2, | vg
hL2 x4/hM2
PL2, and for smaller
PM2, | vg 
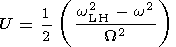
 U /
U / 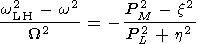
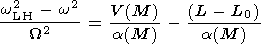

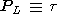


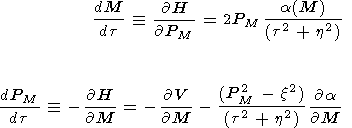
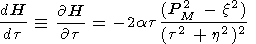
 (wLH2
- w2)max,
so that such a situation appears when
w (wLH)max.)
In this case the wave passes over the potential maximum. Then the
quantity
H varies according to (24), and as was shown
above, for
a > 0 it decreases over the greater part of the
profile. Thus the wave becomes trapped between the potential wall
and the potential maximum.
In this consideration we assumed
t
(wLH2
- w2)max,
so that such a situation appears when
w (wLH)max.)
In this case the wave passes over the potential maximum. Then the
quantity
H varies according to (24), and as was shown
above, for
a > 0 it decreases over the greater part of the
profile. Thus the wave becomes trapped between the potential wall
and the potential maximum.
In this consideration we assumed
t

