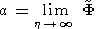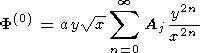International Journal of Geomagnetism and Aeronomy
Vol 1, No. 2, November 1998
A model of the electric field generated by viscous
interaction in the magnetotail plasma sheet
N. V. Erkaev
Computing Center, Krasnoyarsk, Russia
Contents
Abstract
A two-dimensional, time independent
model of the quasi-viscous interaction
of the magnetotail plasma sheet with the streaming solar wind
is discussed in the low viscosity regime
and with the assumption of a
generalized Ohm's law for the electric current.
The role of
viscous forces is most significant in the boundary layers
between
the plasma sheet and solar wind,
and these layers broaden in the downstream direction.
A self-similar solution describing the
distribution of velocity and potential in the boundary layers is
obtained. The solution for the boundary layers determines the
boundary conditions for finding the large-scale distribution of the
electric potential in the plasma sheet.
Introduction
Following
Axford and Hines [1961],
models of quasi-viscous
interaction of the magnetotail plasma sheet with the solar wind
were also discussed by
Krymskiy [1982] and
Pivovarov [1981],
who
based their models on one-fluid MHD equations of the balance of
viscous forces and Ampere forces.
For typical experimental values of the total current and magnetic field
experiment,
these models had to assume a rather large
viscosity in the plasma sheet, which was
difficult to justify physically.
This work presents a two-dimensional model of
the quasi-viscous interaction in which the conductivity is
high and the viscosity is low.
The effect of the viscous forces is mainly concentrated in the
boundary layers adjacent to the magnetopause. The generalized Ohm's
law allowing for the electron pressure anisotropy is used for the
electric current.
Problem Statement
 Consider a semi-infinite plasma sheet (Figure 1) with dimensions
2d in the dawn-dusk direction and
2d in the north-south direction
thick permeated by a magnetic field with a normal component
B0. On the plasma sheet lateral walls adjacent
to the solar wind
are prescribed the plasma velocity
u0 and electric potential
F0 that depend on the
interplanetary magnetic field (IMF),
the origin of which is
associated with reconnection or diffusion of the magnetic field at the
magnetopause. Introduce the Cartesian coordinate system
X, Y, Z, wherein the
X axis is directed away from Earth, downstream, the
Z axis is northward, and the
Y axis is directed toward "dawn."
We will consider the plasma stream only in the
X, Y plane. In this
case, the system of equations for ions has the form
Consider a semi-infinite plasma sheet (Figure 1) with dimensions
2d in the dawn-dusk direction and
2d in the north-south direction
thick permeated by a magnetic field with a normal component
B0. On the plasma sheet lateral walls adjacent
to the solar wind
are prescribed the plasma velocity
u0 and electric potential
F0 that depend on the
interplanetary magnetic field (IMF),
the origin of which is
associated with reconnection or diffusion of the magnetic field at the
magnetopause. Introduce the Cartesian coordinate system
X, Y, Z, wherein the
X axis is directed away from Earth, downstream, the
Z axis is northward, and the
Y axis is directed toward "dawn."
We will consider the plasma stream only in the
X, Y plane. In this
case, the system of equations for ions has the form
The system of equations must be supplemented with the Ohm's law which, with
allowance for drift currents, has the form
+ (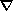 xP
xP / (ne)) + b
(
/ (ne)) + b
(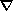 yF
+ uB0 / c -
yF
+ uB0 / c - 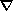 yP
yP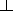 / (ne))
/ (ne))
- b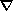 xF + b (
xF + b (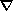 xP
xP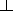 / (ne)) -
/ (ne)) - 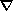 y
F - uB0 / c
+
y
F - uB0 / c
+ 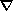 yP
yP / (ne))
/ (ne))
Here
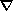 x and
x and
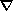 y are the operators
of
differentiation with respect to
x and
y,
s = ne2t/m
is the plasma conductivity along the magnetic field,
P| and
P
y are the operators
of
differentiation with respect to
x and
y,
s = ne2t/m
is the plasma conductivity along the magnetic field,
P| and
P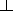 are the field-aligned
and transverse pressures,
R is the field line
curvature radius,
n is the particle density,
r = mpn
is the
mass density of ions,
e is the electron charge,
m is the electron
mass,
c is the speed of light,
b = eB0t/mc
is the magnetization parameter,
t is the characteristic time of collision,
u and
v are the velocity components,
F is the electric potential,
and
B0 is the magnetic field vector component normal
to the neutral
sheet, which we consider prescribed. The current density vector
components are linked by the continuity equation
are the field-aligned
and transverse pressures,
R is the field line
curvature radius,
n is the particle density,
r = mpn
is the
mass density of ions,
e is the electron charge,
m is the electron
mass,
c is the speed of light,
b = eB0t/mc
is the magnetization parameter,
t is the characteristic time of collision,
u and
v are the velocity components,
F is the electric potential,
and
B0 is the magnetic field vector component normal
to the neutral
sheet, which we consider prescribed. The current density vector
components are linked by the continuity equation
Substituting in the last equation the current density components
defined from the Ohm's law yields the electric potential equation:
Here
W is the velocity vortex. Hereinafter, assuming
for
simplicity that the plasma density, pressure, and field line curvature
are constant, we will be interested in the electric potential
distribution and convection velocity field. In this case, the last
equation becomes much simpler and takes the form
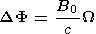 | (1) |
In this context, taking into account the character of the
assumptions made, we will be interested in the description of only
a distant enough part of the magnetotail ( X > 20RE, where
RE is the
Earth's radius).
By cross differentiating the motion equations, one can eliminate the
pressure and obtain the vorticity equation:
Assuming that the magnetic field normal component is
independent of
x,
y yields the following equation for the vorticity
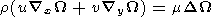 | (2) |
We introduce a current function
y,
in terms of which
the velocity components are given by
 | (3) |
Differentiating the last two equations yields the relationship of
the current function and vorticity:
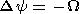 | (4) |
Equations (1)-(4) form a closed system for the functions
W, u, v, F
, and
y.
Boundary Conditions
Consider the boundary conditions at the flanks of the plasma sheet,
where it borders on the solar wind. We will assume that the
velocity components are given here: the tangential component equals
the solar wind speed,
u = u0, and the normal component is zero,
v = 0. Therefore the current function should meet the conditions at the
boundary:
The electric potential is also assumed to be given:
F|y=d =
F0 F|y=
- d = - F0
The equation is linear in relation to the electric potential;
therefore solution for an arbitrary
F can be presented in the
form of the sum
F = F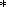 + F0y/d
,
where
F
+ F0y/d
,
where
F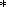 is a solution obtained with zero
boundary condition for the potential, corresponding to a purely
quasi-viscous interaction.
is a solution obtained with zero
boundary condition for the potential, corresponding to a purely
quasi-viscous interaction.
Reduction to Dimensionless Form
Introduce dimensionless variables using the following
normalizations:
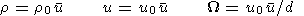 | (5) |
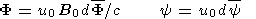 | (6) |
Hereinafter we will omit the bar over the function
designations for simplicity. In so doing, we will consider the
variables made dimensionless by the above formulae. Changing to
dimensionless variables yields the system of equations
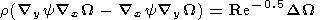 | (7) |
 | (8) |
Here Re is the Reynolds number that depends on the viscosity
coefficient:
Re = u0d / m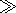 1.
1.
Boundary Layer Method
Taking into account that
Re 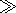 1, we will solve the problem by the
boundary layer method, which is widely used in calculations of
viscous streams at large Reynolds numbers
[Loitsyanskiy, 1978].
Let
us express the unknown function in the form of a sum of rapidly
varying and slowly varying functions:
1, we will solve the problem by the
boundary layer method, which is widely used in calculations of
viscous streams at large Reynolds numbers
[Loitsyanskiy, 1978].
Let
us express the unknown function in the form of a sum of rapidly
varying and slowly varying functions:
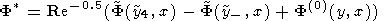 | (9) |
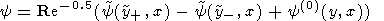 | (10) |
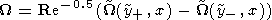 | (11) |
 | (12) |
The first two terms describe the boundary layers at the lateral
boundaries of the plasma sheet at
y=1 and
y=-1.
Using an expansion of the solution of the type (9)-(12) and
substituting it into the equation system yield,
in the asymptotic limit
Re
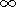 two systems. The first system allows
determination of the boundary functions designated by the tilde. Since
both boundary layers are absolutely symmetric, it will be enough to
calculate one of these. To ensure determinacy, consider the
equations of the boundary layer near the dusk boundary of the
plasma sheet:
two systems. The first system allows
determination of the boundary functions designated by the tilde. Since
both boundary layers are absolutely symmetric, it will be enough to
calculate one of these. To ensure determinacy, consider the
equations of the boundary layer near the dusk boundary of the
plasma sheet:
 | (13) |
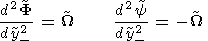 | (14) |
The second system allows us to find a large-scale solution overlapping
with the boundary one:
 | (15) |
Since the number of the sought functions has increased, additional
boundary conditions are needed. First, boundary functions should
meet the condition of approaching zero as the
boundary layer variable tends to infinity:
y+ 
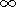 , y-
, y-
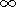 :
:
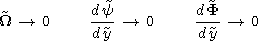 | (16) |
At the boundaries at
y=1 and
y=-1, we have the conditions for the
electric potential and velocity components
 | (17) |
 | (18) |
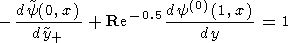 | (19) |
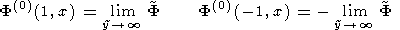 | (20) |
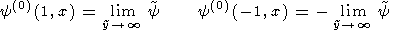 | (21) |
In a zero approximation in the parameter
Re-0.5, we have
Self-Similar Solution of Boundary Layer Equations
Introduce the self-similar variables
h = y / x
x = y
/ x
f = F
/ x w = W
/ x
Then the boundary layer equations are transformed into ordinary
differential equations
Sought is a solution that meets the boundary conditions
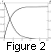 Figure 2 shows the boundary layer functions obtained as a result
of
numerical integration of a self-similar system and
satisfying the
boundary conditions (16) and (19).
Figure 2 shows the boundary layer functions obtained as a result
of
numerical integration of a self-similar system and
satisfying the
boundary conditions (16) and (19).
Determination of Potential Outside Boundary Layers
Outside the boundary layers we have the Laplace equation
DF(0)
= 0
Boundary conditions at the edges of the region under calculation
are obtained from the conditions of asymptotic matching with the
boundary layer solution:
F(0)(1, x) =
ax F(0)
(- 1, x) = - ax
Constant
a is defined by numerical integration of equation system
of the boundary layer.
With a view to obtaining an analytical solution, we will represent
the potential in the form of the series
which satisfies the Laplace equation on the condition that the
expansion coefficients are linked by the recurrence relationship:
The series absolutely converges at
|y / x| < 1.
Note that no boundary conditions at the section
x=1 were discussed
for the potential. Uncertainty of this condition in this problem is
associated with the exclusion from discussion of the head section
of the magnetosphere. In the general case, the correction to the
above solution should satisfy the Laplace equation with zero
conditions at
y=-1,
y=1 and the prescribed condition at
x=1.
The solution of such a problem decays quite fast with increasing
x.
Therefore, the effect of the additional condition should
significantly weaken when moving away from Earth toward the
magnetotail.
Discussion
 Figure 3 shows the diagrams of variation of the electric potential
and velocity in the dusk-dawn direction at a distance of
x=2.5d.
With
d=20 RE, this distance is
50 RE The dashed lines correspond to Re
= 1000, and the solid
lines correspond to Re
=100.
Figure 3 shows the diagrams of variation of the electric potential
and velocity in the dusk-dawn direction at a distance of
x=2.5d.
With
d=20 RE, this distance is
50 RE The dashed lines correspond to Re
= 1000, and the solid
lines correspond to Re
=100.
 The potential decreases in the dusk boundary layer from zero at the
magnetopause to a minimum negative value and then increases nearly
linearly to a positive maximum, and in the dawn boundary layer it
again decreases to zero at the magnetopause. The maximum and
minimum of the potential depend on the Reynolds parameter.
According to Figure 3, the overall difference of potentials across
the plasma sheet amounts to
0.16u0B0d/c
at Re
=1000 and
0.34u0B0d/c
at Re
=100. Assuming
B0=1 nT,
u0=400 km s
-1,
d=20 RE, and
c=3
The potential decreases in the dusk boundary layer from zero at the
magnetopause to a minimum negative value and then increases nearly
linearly to a positive maximum, and in the dawn boundary layer it
again decreases to zero at the magnetopause. The maximum and
minimum of the potential depend on the Reynolds parameter.
According to Figure 3, the overall difference of potentials across
the plasma sheet amounts to
0.16u0B0d/c
at Re
=1000 and
0.34u0B0d/c
at Re
=100. Assuming
B0=1 nT,
u0=400 km s
-1,
d=20 RE, and
c=3  1010 cm s
-1,
we will have numerical estimates of
the difference of potentials:
F max - F
min
1010 cm s
-1,
we will have numerical estimates of
the difference of potentials:
F max - F
min 8 kV at
Re
=1000 and
F max - F
min
8 kV at
Re
=1000 and
F max - F
min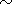 17 kV at Re
=100. The
points of turning to zero in the velocity coincide with the points of maximum and
minimum electric potential. The distance between the magnetopause
and the point of zero velocity is
0.2d at Re
=1000 and
0.35d at
Re
=100. In the middle of the layer, plasma moves earthward at a
speed of
0.1u0 at Re
=1000 and
0.33u0 at Re
=100. Figure 4a,
b
show the electric potential isolines in the plasma sheet plane.
The coordinates are normalized to the half width of the plasma layer
d.
17 kV at Re
=100. The
points of turning to zero in the velocity coincide with the points of maximum and
minimum electric potential. The distance between the magnetopause
and the point of zero velocity is
0.2d at Re
=1000 and
0.35d at
Re
=100. In the middle of the layer, plasma moves earthward at a
speed of
0.1u0 at Re
=1000 and
0.33u0 at Re
=100. Figure 4a,
b
show the electric potential isolines in the plasma sheet plane.
The coordinates are normalized to the half width of the plasma layer
d.
Now we will try to estimate the Reynolds parameter. According to
its definition,
Re = ru0d
/ m.
The viscosity coefficient
m can be
estimated by the formula
rvtl, where
vt is the
thermal velocity of ions, and
l is the free path length. If one
assumes that the effective free path length is comparable
in magnitude with the Larmor radius, then the following
estimate can be obtained:
where
k is the Boltzmann constant,
mp is the proton mass,
vp is the thermal velocity of the proton,
T is the temperature of proton
in the plasma sheet,
c is the speed of light, and
e is the electron
charge. Note that in the last formula
the complete magnetic field modulus
B should be substituted,
which comprises a more
significant
Bx component and determines the Larmor radius.
Using the last equality and assuming
[Akasofu and Chapman, 1972]
Tp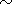 5107 K
B = 10 nT
5107 K
B = 10 nT
u0 = 400 km s-1
d = 20 RE
yields an estimate of the Reynolds parameter:
Conclusions
A two-dimensional model of
the quasi-viscous interaction of the magnetotail plasma sheet with the
streaming solar wind is discussed in the low viscosity regime.
The role of viscous forces is
most significant in the boundary layers that widen while receding
downstream and are situated along the boundaries of the plasma
sheet and solar wind. The motion of plasma in boundary layers
permeated by the magnetotail magnetic field results in its
polarization and occurrence of the dawn-dusk potential difference
that depends on the effective turbulent viscosity. At a zero IMF
and parameters of
u0=400 km s
-1 and
B0=1 nT, the potential
difference is 8-17 kV for Reynolds numbers 1000-100. In this
context, the boundary layer thickness is
4 RE - 7 RE
. At the
internal boundaries of the boundary layers, the plasma velocity
along the tail and the electric field across the tail are zero.
Thus the boundary layer boundaries are the lines of changes in
direction of plasma convection from tailward to earthward.
The Reynolds number of the order of 100 corresponds to the
suggestion that the effective free path length of ions equals, in
order of magnitude, their Larmor radius. With an IMF other than
zero, an additional electric field associated with reconnection
arises
[Denisenko et al., 1992;
Erkaev, 1988],
which is summed
with the quasi-viscous interaction field. For example, southward
IMF reinforces earthward convection in the plasma sheet, and
northward IMF suppresses it.
The theory discussed provides a good description of the physical
processes involved and their interaction. However for the preferred
value of Re
=100, the boundary layer thickness is
7 RE and the
earthward convection velocity in the central plasma sheet is
~130 km s
-1. These values are rather large, especially
since the convection speed would be increased for the case of
southward IMF.
Acknowledgments
This work was supported by the International
Science Foundation (project RKN300) and by the Russian
Foundation for Basic Research (project 9505-14192).
References
Akasofu, S.-I., and S. Chapman, Solar-Terrestrial Physics, 512 pp.,
Clarendon, Oxford, England, 1972.
Axford, W. I., and S. O. Hines, A unifying theory of high-latitude
geophysical phenomena and geomagnetic storms, Can. J. Phys., 39,
1443, 1961.
Denisenko, V. V., N. V. Erkaev, A. V. Kitaev, and I. T. Matveenkov,
Mathematical Modeling of Magnetospheric Processes, 197 pp., Nauka, Novosibirsk,
1992.
Erkaev, N. V., The results of research of MHD flow past the
magnetosphere, Geomagn. Aeron., 28 (4), 529, 1988.
Krymskiy, P. F., A model of energy transfer in the Earth's
magnetosphere, Issled. Geomagn. Aeron. Fiz. Sol., 62, 3, 1982.
Loitsyanskiy, L. G., Mechanics of Liquid and Gas, 736 pp., Nauka, Moscow,
1978.
Pivovarov, V. G., The effects of viscous interaction of the solar
wind with the tail plasma sheet, Geomagn. Aeron., 5, 876, 1981.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.2.0) on November 4, 1998.
 Consider a semi-infinite plasma sheet (Figure 1) with dimensions
2d in the dawn-dusk direction and
2d in the north-south direction
thick permeated by a magnetic field with a normal component
B0. On the plasma sheet lateral walls adjacent
to the solar wind
are prescribed the plasma velocity
u0 and electric potential
F0 that depend on the
interplanetary magnetic field (IMF),
the origin of which is
associated with reconnection or diffusion of the magnetic field at the
magnetopause. Introduce the Cartesian coordinate system
X, Y, Z, wherein the
X axis is directed away from Earth, downstream, the
Z axis is northward, and the
Y axis is directed toward "dawn."
We will consider the plasma stream only in the
X, Y plane. In this
case, the system of equations for ions has the form
Consider a semi-infinite plasma sheet (Figure 1) with dimensions
2d in the dawn-dusk direction and
2d in the north-south direction
thick permeated by a magnetic field with a normal component
B0. On the plasma sheet lateral walls adjacent
to the solar wind
are prescribed the plasma velocity
u0 and electric potential
F0 that depend on the
interplanetary magnetic field (IMF),
the origin of which is
associated with reconnection or diffusion of the magnetic field at the
magnetopause. Introduce the Cartesian coordinate system
X, Y, Z, wherein the
X axis is directed away from Earth, downstream, the
Z axis is northward, and the
Y axis is directed toward "dawn."
We will consider the plasma stream only in the
X, Y plane. In this
case, the system of equations for ions has the form
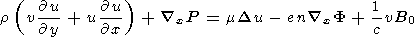
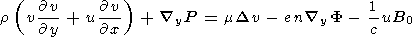
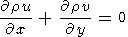
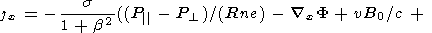
 xP
xP / (ne)) + b
(
/ (ne)) + b
(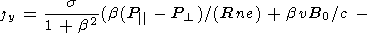
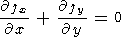
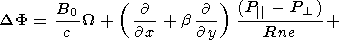
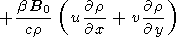
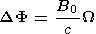
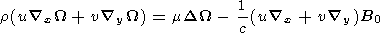
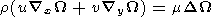

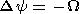

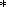 + F0y/d
,
where
F
+ F0y/d
,
where
F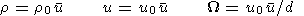
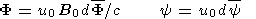
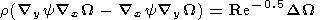

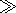 1.
1.
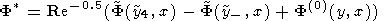
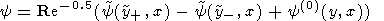
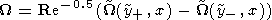


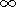 two systems. The first system allows
determination of the boundary functions designated by the tilde. Since
both boundary layers are absolutely symmetric, it will be enough to
calculate one of these. To ensure determinacy, consider the
equations of the boundary layer near the dusk boundary of the
plasma sheet:
two systems. The first system allows
determination of the boundary functions designated by the tilde. Since
both boundary layers are absolutely symmetric, it will be enough to
calculate one of these. To ensure determinacy, consider the
equations of the boundary layer near the dusk boundary of the
plasma sheet:

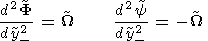

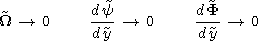


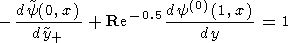
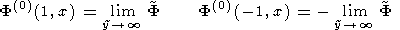
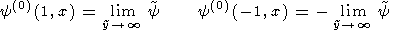



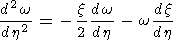


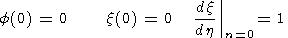
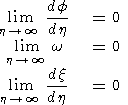
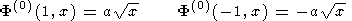


 1010 cm s
-1,
we will have numerical estimates of
the difference of potentials:
F max - F
min
1010 cm s
-1,
we will have numerical estimates of
the difference of potentials:
F max - F
min 8 kV at
Re
=1000 and
F max - F
min
8 kV at
Re
=1000 and
F max - F
min