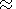 3 , and at 3 < L < 8 is well
approximated by the dependence p
3 , and at 3 < L < 8 is well
approximated by the dependence p 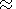 L
L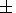 0.22 .
At L < 5 , a strong anisotropy of pressure is observed
( p
0.22 .
At L < 5 , a strong anisotropy of pressure is observed
( p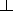
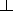
E. E. Antonova and B. A. Tverskoy
Nuclear Physics Research Institute, Moscow State University, Moscow, Russia
The development of the quantitative theory of magnetosphere-ionosphere coupling (first works in this direction were Tverskoy [1969, 1972], Vasyliunas [1972]) and the experimental observation technique has allowed us to explain many specific features of large-scale magnetospheric convection and to highlight the problems which still remain unresolved. The goal of this paper is to consider the most significant aspects of the available theoretical approaches to this problem, including the nature of the dawn-dusk electric field and mechanisms of field screening in the inner magnetosphere. Major attention will be paid to those research directions which have not been discussed in the literature thoroughly enough, but which allow us to eliminate the discrepancy between the existing theoretical descriptions and the experimental data. At first we discuss the role of azimuthal pressure gradients in formation of the field-aligned current system and magnetospheric convection. Then we consider peculiarities of solution of the stationary and nonstationary linear problems of magnetospheric convection and their applicability to the description of the experimental data. Attention will also be given to the role of diffusion processes in formation of the quasi-stationary plasma distribution and to the problem of the convection crisis.
Though satellite measurements in the near-Earth space plasma have
been performed for a long time, there is still no sufficiently
complete picture of distribution of the plasma pressure in the
magnetospheric cavity. It has been shown experimentally (see
references in the review of
Tsyganenko [1990])
that across the
magnetotail, the condition p + Bx2/8p = ! const, where p is the
hot magnetospheric plasma pressure in the central regions of the
plasma sheet close to the isotropic region
[ Christon et al., 1991;
Lui and Hamilton, 1992;
Stiles et al., 1978]
and Bx is the
field-aligned (along the tail) magnetic field component, is
satisfied with a high degree of accuracy. According to the data of
AMPTE/CCE
[ Lui and Hamilton, 1992],
in magnetically quiet
conditions, the pressure at the geocentric distances (2.5-9) RE (where RE is the Earth's radius) only slightly depends on the
azimuthal angle, peaks at L 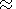 3 , and at 3 < L < 8 is well
approximated by the dependence p
3 , and at 3 < L < 8 is well
approximated by the dependence p 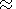 L
L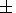 0.22 .
At L < 5 , a strong anisotropy of pressure is observed
( p
0.22 .
At L < 5 , a strong anisotropy of pressure is observed
( p
It has long been believed that, solving the problem of flowing
around of the magnetosphere by the solar wind plasma, one can neglect in the first approximation the presence
of hot plasma in the cavity and, hence, the
nondipole sources of magnetic field. In
this case the existence of the geomagnetic tail was qualitatively
attributed to
However, near the dayside magnetopause, the point on the field line where the field strength is minimum does not lie in the equatorial plane, but at high latitudes (this effect is typically considered in connection with splitting of particle drift shells [ Shabanskiy, 1972]), where the hot plasma pressure is already comparable to the magnetic pressure and dynamic pressure of the solar wind (the near-cusp region). Therefore, in solving the problem of flow, taking into account filling of the cavity with plasma can prove to be a key factor in estimating the effect of the solar wind magnetic field on the distribution of fields and currents in the magnetosphere and, hence, on the geomagnetic activity. For instance, the studies carried out by Sibeck et al. [1991] and Tsyganenko and Sibeck [1994] showed that changes in the position of the magnetopause during variation of the interplanetary magnetic field (IMF) result from changes in the magnetic field of the intramagnetospheric sources (field-aligned current and tail current), and not by processes of the reconnection type.
The role of azimuthal pressure gradients of hot magnetospheric
plasma in the formation of the region II currents of
Iijima and Potemra [1976]
is well known. The picture is not that clear for the
region I currents. The
Iijima and Potemra [1976]
picture of the
region I current densities gave maxima at 1000 and 1400 MLT.
According to the magnetic field models such regions can be projected
onto the magnetosphere boundary layers, whereas the other main part
of the region I currents is projected onto the plasma sheet. The
results of such projection lead
Stern [1983\link
The major difficulty encountered by the concept of generation of the dawn-dusk potential difference in the magnetosphere by the processes occurring in the magnetospheric boundary layers is the localization of these fields. According to the available magnetospheric models [ Tsyganenko, 1990], the magnetospheric boundary layers are projected onto the near-cusp regions, and the field-aligned currents of region I are distributed over the polar edge of the auroral oval. Feldstein and Galperin [1985], Galperin and Feldstein [1989], and Elphinstone et al. [1991] showed that the auroral oval is projected onto the inner regions of the plasma sheet. Correspondingly, the maximum potential drop between the morning and evening sides of the magnetosphere takes place deep inside the plasma sheet, rather than at the polar cap boundary, which is hardly consistent with the field penetration from the solar wind.
The mechanism of creation of the dawn-dusk field by the azimuthal pressure gradients does not require the assumption of equipotentiality of magnetic field lines, which apparently can be violated elsewhere than in the region of strong field-aligned currents flowing from the ionosphere. The mechanism is based on the assumption of the fulfillment of the condition of magnetostatic equilibrium for the velocities of plasma motion much less than the sound and Alfv\'en velocities. In the case of isotropy of plasma pressure this condition is given by
 | (1) |
where j is the transverse current density, B is the magnetic field, and c is the velocity of light (in case of anisotropic plasma pressure)
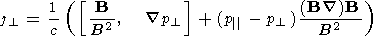 |
Since in the magnetospheric regions of major interest for the problem considered the pressure is close to isotropic [ Christon et al., 1991; Lui and Hamilton, 1992; Stiles et al., 1978], in what follows we shall use (1). The consequence of (1) is the expression for the field-aligned current density at ionospheric altitudes [ Tverskoy, 1982; Vasyliunas, 1970]
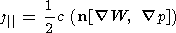 | (2) |
where n is the vector of the normal to ionosphere, W = dl/B is
the magnetic field tube volume, dl is the element of the magnetic
field line length, and is the two-dimensional gradient. Both W and P are analyzed as functions of latitude and longitude in the
ionosphere. The dependence of j
Equation (2), together with the equation for current continuity in the ionosphere (see Appendix A), gives the basic equation for the low-frequency magnetosphere-ionosphere coupling in the high-latitude approximation [ Tverskoy, 1982, 1983]
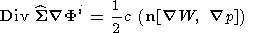 | (3) |
where 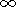 . In the first case, the
field-aligned current is zero and the condition of the magnetostatic
equilibrium reduces to the condition that constant-pressure surfaces
coincide with constant volume surfaces, an assumption that is
commonly used in the physics of laboratory plasma. In the second
case, when conductivity tends to
. In the first case, the
field-aligned current is zero and the condition of the magnetostatic
equilibrium reduces to the condition that constant-pressure surfaces
coincide with constant volume surfaces, an assumption that is
commonly used in the physics of laboratory plasma. In the second
case, when conductivity tends to 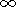 , the equilibrium electric
fields become zero.
, the equilibrium electric
fields become zero.
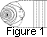 It follows from (1) and (3) that the presence of the magnetostatic
equilibrium field-aligned currents in the cavity can be revealed not
only by determining the projection of W on the magnetic field line,
which is beyond the accuracy limits of the available magnetic field
models
[ Tsyganenko, 1990]
and presents difficulties for experimental
measurements, but also by analyzing the distribution of lines of
constant W and current lines in the equatorial plane (Figure 1).
Since ( j p) = 0 ,
the noncoincidence of the current lines and
lines of constant W leads, according to (3), to the existence of
field-aligned currents. The case of generation of field-aligned
currents corresponding in sign to the current system I of
Iijima and Potemra [1976]
(the current enters from the morningside and exits
from the eveningside) corresponds to the larger curvature of
isolines W =! const than of the current lines in the equatorial plane,
as shown in Figure 1.
Antonova and Ganyushkina [1995a]
showed that
the semiempirical magnetic field models Tsyganenko 87 and
Tsyganenko 87W
[ Peredo et al., 1993]
conform to just this
qualitative picture.
It follows from (1) and (3) that the presence of the magnetostatic
equilibrium field-aligned currents in the cavity can be revealed not
only by determining the projection of W on the magnetic field line,
which is beyond the accuracy limits of the available magnetic field
models
[ Tsyganenko, 1990]
and presents difficulties for experimental
measurements, but also by analyzing the distribution of lines of
constant W and current lines in the equatorial plane (Figure 1).
Since ( j p) = 0 ,
the noncoincidence of the current lines and
lines of constant W leads, according to (3), to the existence of
field-aligned currents. The case of generation of field-aligned
currents corresponding in sign to the current system I of
Iijima and Potemra [1976]
(the current enters from the morningside and exits
from the eveningside) corresponds to the larger curvature of
isolines W =! const than of the current lines in the equatorial plane,
as shown in Figure 1.
Antonova and Ganyushkina [1995a]
showed that
the semiempirical magnetic field models Tsyganenko 87 and
Tsyganenko 87W
[ Peredo et al., 1993]
conform to just this
qualitative picture.
By closing in the ionosphere, the field-aligned currents create the large-scale dawn-dusk field which requires for its support only the presence of corresponding azimuthal pressure gradients or, equivalently, a definite geometry of the W = ! const surfaces. The effect of the IMF on the dawn-dusk electric field is attributable to changes in the configuration of the magnetospheric current systems and the magnitudes of currents in them. Antonova and Ganyushkina [1995b] showed that for southward IMF, the angle between the isolines W =! const and current lines increases, and, hence, the region I currents increase. Therefore in solving the problem of the IMF effect on magnetospheric activity it is not the electric field penetration into the magnetosphere, but changes in the currents in the tail and on the magnetopause that should be explained. However, as noted above, this cannot be explained in the framework of the model of flow of an empty cavity. From the information about the distribution of field-aligned currents at ionospheric altitudes [ Iijima and Potemra, 1976] and calculations of the volumes of magnetic field tubes and their gradients [ Antonova and Ganyushkina, 1994; Antonova et al., 1993], Antonova and Ganyushkina [1995c] estimated the pressure gradients needed to sustain field-aligned currents. It was shown that the magnetospheric cavity contains enough plasma to maintain the calculated pressure gradients both for currents of region II and for region I currents (because of appreciably lower p , relatively larger pressure gradients are required for region II currents). The obtained day-night pressure differences proved to be comparable with pressure magnitudes at corresponding geocentric distances measured in the AMPTE/CCE experiment [ Lui and Hamilton, 1992], which apparently hampers the use of the linear approximation for description of the magnetospheric convection.
The question arises as to what are the conditions for which isolines W =! const will coincide with the current lines and the field-aligned current will not be generated. First of all, this will occur for the cavity with the azimuthal symmetry (the region of dipole field lines in the Earth's magnetosphere), where isolines W = ! const and current lines in the equatorial plane are concentric circles. Field-aligned currents will also not be generated in fields with translational invariance where W =! const and current lines are parallel straight lines. The plasma sheet regions remote from the Earth are close to the latter configuration. There still remains the question of whether isolines W =! const and current lines can coincide in a strongly asymmetrical part of the magnetospheric cavity where the field lines transform from a dipole configuration to one extending into a tail. Note that in the absence of the electric field in the magnetosphere the plasma sheet should have disappeared due to the ion drift through the morningside to the eveningside (on the order of several hours). To sustain the plasma sheet in steady state, particles should be constantly injected into the magnetosphere from the morningside and ejected into the evening part of the low-latitude boundary layer from the eveningside. In this case plasma should have been heated at first from the temperature of the boundary layer to that of the plasma sheet (approximately by an order of magnitude) and then cooled again, which seems to be highly improbable. The existence of a constant earthward directed plasma flow caused by the presence of the dawn-dusk field is therefore the necessary condition for the existence of the plasma sheet in quasi-equilibrium. Ashour-Abdalla et al. [1993, 1994] studied in detail the processes of such a formation in the one-particle approximation for a given distribution of the electric and magnetic fields.
During magnetospheric substorms, the cavity is quickly replenished by heated and accelerated particles. Since substorms mainly occur for the southward directed IMF, in the case of negative IMF a source acts periodically in the inner magnetospheric regions (at L = 7-10 ) increasing the magnetospheric plasma pressure. The ensuing state is not magnetostatically balanced in the majority of cases. The excess of the formed particles is ejected in the form of a plasmoid into the distant regions of the magnetospheric tail.
Observations also reveal a destruction of the plasma sheet during long periods of the northward orientation of the IMF and reduced geomagnetic activity. For positive IMF, compression of the auroral oval occurs, and arcs are formed in the polar cap, which Frank et al. [1986] called the theta aurora. According to the observations [ Frank et al., 1986; Huang et al., 1989a], the appearance of the theta aurora is associated with penetration of the plasma of the plasma sheet into the tail parts, which is quite naturally interpreted as bifurcation of the plasma sheet (formation of the plasma structure of the Maltese-cross type). The disappearance of the plasma sheet during a long-lasting positive IMF was detected by the ISEE 3 satellite [ Fairfield, 1993]. The observed phenomena are most probably associated with violation of equilibrium between the plasma pressure and magnetic pressure due to the current weakening in the tail. In this case the theta aurora current system (the outflow of the field-aligned current on the morningside and inflow on the eveningside) and the presence of the electric field directed from dusk toward dawn in the polar cap can be explained quite easily [ Antonova and Ganyushkina, 1995b]. Note that the plasma system has a minimum energy if it is without power, i.e., pressure gradients are absent in it, and the destruction of the plasma sheet for positive IMF can therefore be regarded as a natural process of transition of the magnetosphere into the state with the lowest energy.
The discussed approach to the description of the process of formation of large-scale magnetospheric convection makes it possible to relate the processes in the magnetospheric boundary layers to the disturbances of the plasma motion in the regions of projection of boundary layers at the ionospheric altitudes, i.e., in daytime hours. Thus the difficulties of the theory of large-scale reconnection are obviated. The solar wind energy is transmitted to the magnetosphere through its current systems. The most complicated point of the gradient mechanism of convection is maintenance of the quasi-stationary state in the conditions of regular plasma motion, at which isosurfaces W = const intersect. This problem will be discussed below when considering the problem of "convection crisis."
It is possible to perform the analytical consideration of the
problem of plasma stability in the cavity for b = 8pp/B2 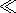 1 ,
which is valid for the processes in the region of dipole field
lines and, in part, at the inner edge of the plasma sheet. Since the
properties of the obtained solutions allow us to explain many
specific features of intramagnetospheric processes, we discuss in
detail the assumptions used for solving this problem and properties
of the solutions.
1 ,
which is valid for the processes in the region of dipole field
lines and, in part, at the inner edge of the plasma sheet. Since the
properties of the obtained solutions allow us to explain many
specific features of intramagnetospheric processes, we discuss in
detail the assumptions used for solving this problem and properties
of the solutions.
In solving the problem of large-scale magnetosphere-ionosphere
coupling, two questions arise which have no final solution at
present. It is necessary to know the relation between the potential
variations in the magnetosphere and ionosphere and to find the
relation between the pressure changes and changes of the
magnetospheric potential. It is typically assumed in solving the
problem of magnetosphere-ionosphere coupling that because of a high
plasma conductivity the magnetic field lines can be considered to be
equipotential. The difficulty encountered in checking this
assumption is connected with the small number of simultaneous
measurements of the electric field at one and the same field line.
Weimer et al. [1985]
reports the results of four measurements of
this type by DE 1 and DE 2 satellites. It was shown that at
invariant latitudes of 55-60o, the identical electric field
variations were detected at the altitudes of 800 km and 12,000 km.
However, at latitudes of 65-70o, variations in the
magnetospheric potential appreciably exceeded the ionospheric
potential variations. To elucidate the dependence of potential
variation on the scale of disturbance, the Fourier analysis of
fluctuations was performed. It was shown that for the scale 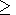 1000 km, in the projection on the ionospheric altitudes, the potential
fluctuations in the magnetosphere and ionosphere coincide, and for
the scale of less than 200 km the field lines cannot be considered
to be equipotential. In this case, the dependence
1000 km, in the projection on the ionospheric altitudes, the potential
fluctuations in the magnetosphere and ionosphere coincide, and for
the scale of less than 200 km the field lines cannot be considered
to be equipotential. In this case, the dependence
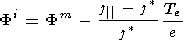 | (4) |
obtained by
Knight [1973] and
Antonova and Tverskoy [1975] and
experimentally verified by
Lyons [1981] and
Bosqued et al. [1986]
for the inverted V type structures "works" well. Here, Fm is the
potential in the magnetosphere, j*= e ne Te
Such an isotropization can be the consequence of both the conventionally studied processes of quasi-linear relaxation of anisotropic functions of particle distribution (the studies were started for the magnetosphere by Kennel [1966] and significantly advanced by Bespalov and Trachtengertz [1986] and Lyons and Williams [1984]) and violation of the adiabaticity of motion due to the nonlinear potential disturbances comparable with the Larmor radius of electrons. Note that under the condition of developed turbulence, appreciable field-aligned electric fields and relevant potential variations giving, on the whole, a zero contribution to the acceleration process can exist at the field line above the region of acceleration of electrons giving rise to the inverted V type structures. This altitude region is still little studied. The existence of irregularities in the electric potential must lead to the nonadiabaticity of the ion motion as well. So far stochastization of the ion motion has been studied in detail only for the case when the Larmor radius of an ion is comparable with the scale of the magnetic field inhomogeneity [ Buchner and Zelenyi, 1989; Chen and Palmadesso, 1986]. Note that observations of the fields in the plasma sheet reveal strong fluctuations in both the electric and magnetic components [ Petersen et al., 1982], and the electric field fluctuations are often not accompanied by the magnetic field fluctuations. On the whole, it is most likely that the condition of equipotentiality of magnetic field lines is satisfied neither for the regions with fairly strong field-aligned currents flowing from the ionosphere and exceeding the limit provided by a free gas dynamic outflow of electrons from the magnetic field tube into the ionosphere nor for sufficiently long magnetic field lines extended into a tail. However, the equipotential approximation describes fairly well the physics of the process for sufficiently large-scale disturbances at the inner edge of the plasma sheet. This simplification makes it possible to reduce the three-dimensional problem to the two-dimensional one.
In the linear approximation (see Appendix B and C), it is assumed that the undisturbed plasma distribution is independent of the azimuthal angle (the pressure is constant on W =! const surfaces for the hydrodynamic description of processes) and the disturbance which depends on the azimuthal angle in the stationary problem and on the azimuthal angle and time in the nonstationary problem is small compared with the nondisturbed distribution. The potential disturbance is regarded as being of small magnitude at first order. These assumptions allow us to relate the pressure disturbance to the potential disturbance and to transform the basic equation for the magnetosphere-ionosphere coupling into the equation predicting the potential distribution on the sphere with a given conductivity distribution.
For the first time, the nonstationary problem in the drift approximation was solved by Tverskoy [1969, 1972], and the stationary problem was solved by Vasyliunas [1972] who used significant simplifying assumptions about the properties of plasma (a sharp inner plasma sheet edge and invariability in the number of particles in the magnetic field tube inside the sheet). The results of these works were reviewed and generalized by Pellat and Laval [1972]. Since then, a large number of papers concerned with the Alfv\'en screening of the inner magnetosphere have been published. Among recent publications, the most detailed analysis and review of the earlier obtained results was given by Blanc and Caudal [1985] and Del Pozo and Blanc [1994]. The problem of Alfv\'en screening in the stationary case was reduced to solving the equation for current continuity in the ionosphere for a given potential distribution at the polar cap boundary. In the problem the "magnetospheric conductivity" (exceeding by more than an order of magnitude the ionospheric Hall conductivity) was added to the latter. Therefore, many publications concerning the "electrotechnical" description of the magnetospheric processes appeared (see the book of Lyatskiy [1978] and the references therein).
The electrotechnical approach made it possible to describe a
noticeable weakening of the field equatorward from the auroral oval
in the case of a proper choice of the magnitude of the
"magnetospheric conductivity" and gave the field amplitudes in the
auroral oval close to those experimentally observed. However, the
azimuthal field distribution did not agree with the experimental
data. Indeed, in the stationary case the engendered field-aligned
current with which the inner magnetosphere screening is associated
is proportional to 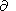 F/
F/ 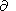 j and therefore, as noted by
Pellat and Laval [1972],
the maximum field-aligned currents must be observed at
night and noon hours. In the experiments, currents of region II are
the highest at the evening and morning hours. Attempts were made to
solve the problem of the "phase shift" by taking into account the
nonuniformity of conductivity and particle injection (see
Peymiat and Fontaine [1994]
and the references therein). For instance,
Peymiat and Fontaine [1994]
showed that taking into account
injection in the regime of a strong pitch angular diffusion can lead
to rotation of the initial electric field distribution by 3 hours,
but this does not give an adequate description of the east-west
component of the electric field. The dawn-dusk maxima of the
field-aligned currents of regions I and II are given by the solution
of the nonstationary problem of convection where the field-aligned
current density is proportional to
j and therefore, as noted by
Pellat and Laval [1972],
the maximum field-aligned currents must be observed at
night and noon hours. In the experiments, currents of region II are
the highest at the evening and morning hours. Attempts were made to
solve the problem of the "phase shift" by taking into account the
nonuniformity of conductivity and particle injection (see
Peymiat and Fontaine [1994]
and the references therein). For instance,
Peymiat and Fontaine [1994]
showed that taking into account
injection in the regime of a strong pitch angular diffusion can lead
to rotation of the initial electric field distribution by 3 hours,
but this does not give an adequate description of the east-west
component of the electric field. The dawn-dusk maxima of the
field-aligned currents of regions I and II are given by the solution
of the nonstationary problem of convection where the field-aligned
current density is proportional to 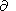 2 F/
2 F/ 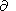 j2 .
j2 .
This result indicates that when the disturbance reaches the steady
state nonlinear regime, the localization of the original disturbance
is preserved and no transition of this disturbance (through rotation
of the azimuthal field component and field-aligned current) to the
configuration predicted by the solution of the stationary linear
problem occurs. The problem of the phase shift does not arise in
numerical models of convection in which particles are injected into
the inner magnetosphere and then travel in the generated
self-consistent field
[ Chen et al., 1982;
Harel et al., 1981a, b\link
 Another aspect of the problem is associated with the radial pressure
profile observed by AMPTE/CCE
[ Lui and Hamilton, 1992].
As noted
above, at L > 3 the magnetospheric pressure decreases monotonically
with increasing radial distance. The solid line in Figure 2 shows
schematically the dependence of pressure on W (in the dipole field W
Another aspect of the problem is associated with the radial pressure
profile observed by AMPTE/CCE
[ Lui and Hamilton, 1992].
As noted
above, at L > 3 the magnetospheric pressure decreases monotonically
with increasing radial distance. The solid line in Figure 2 shows
schematically the dependence of pressure on W (in the dipole field W  L4 ). During magnetospheric substorms, injection of particles
into the inner magnetosphere occurs, and the profile becomes
nonmonotonic (the dot-and-dash line in Figure 2). Let us recall that
for the azimuthally symmetrical distribution of the low-pressure
plasma to be stable, the criterion of
Kadomtsev [1963]
L4 ). During magnetospheric substorms, injection of particles
into the inner magnetosphere occurs, and the profile becomes
nonmonotonic (the dot-and-dash line in Figure 2). Let us recall that
for the azimuthally symmetrical distribution of the low-pressure
plasma to be stable, the criterion of
Kadomtsev [1963]
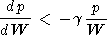 | (5) |
must be satisfied (for the kinetic description ( pL7)' > 0 [ Tverskoy, 1969, 1972]), and therefore a sufficiently slowly decaying monotonic pressure profile is stable with respect to the electric field excitation. In this case the assumption of the localization of currents of region II at L < 3 made by Peymiat and Fontaine [1994] surely contradicts the experimental data. The quasi-stationary azimuthal plasma asymmetry seems to be more probable. We discussed this asymmetry as a source of the current system of region I associated with the magnetic cavity geometry. For the currents of region II, the geomagnetic field is close to that of the dipole and the pressure asymmetry is due to the action of the dawn-dusk field leading to formation of the pressure maximum near midnight. In this situation, the pressure distribution can be maintained monotonic in radius if the p(W) dependence for the daytime (the dashed line in Figure 2) is more abrupt than for the night hours. The data of Lui and Hamilton [1992] do not contradict to this assumption. In order to confirm it, it is desirable to have simultaneous measurements of the radial pressure profile for two local times.
 The injection-induced region of pressure growing with increasing
geocentric distance is the source of nonsteady state convection.
Tverskoy [1969, 1972]
solved the nonstationary linear problem that
allows description of the system of electric fields and currents
generated by such a profile (the dot-and-dash line in Figure 2). In
the case of a power dependence of pressure on L , the problem can be
solved analytically and is of the form of expansion in terms of
Bessel functions if the symmetric part of pressure p(L) = p0(L/L0)
The injection-induced region of pressure growing with increasing
geocentric distance is the source of nonsteady state convection.
Tverskoy [1969, 1972]
solved the nonstationary linear problem that
allows description of the system of electric fields and currents
generated by such a profile (the dot-and-dash line in Figure 2). In
the case of a power dependence of pressure on L , the problem can be
solved analytically and is of the form of expansion in terms of
Bessel functions if the symmetric part of pressure p(L) = p0(L/L0)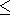 L0 ,
where L0 = 2q0 is the location of the radial
pressure profile maximum. For small injections, the conditions of
the type of |p'|
L0 ,
where L0 = 2q0 is the location of the radial
pressure profile maximum. For small injections, the conditions of
the type of |p'| 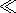 p0 are satisfied. As shown by
Tverskoy [1969, 1972],
even a small deviation from uniform equilibrium gives a
picture which appreciably differs from the observed one. For the
harmonics of the type (-imj) , the eigen functions are in the
form Um = A(q /q0)m for q
p0 are satisfied. As shown by
Tverskoy [1969, 1972],
even a small deviation from uniform equilibrium gives a
picture which appreciably differs from the observed one. For the
harmonics of the type (-imj) , the eigen functions are in the
form Um = A(q /q0)m for q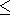 q0 and Unm= B Tm [q0
q0 and Unm= B Tm [q0 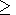 q0 , where A and B are functions of time. The spectrum of
magnitudes of lmn is determined from the condition of
continuity of Umn and U
q0 , where A and B are functions of time. The spectrum of
magnitudes of lmn is determined from the condition of
continuity of Umn and U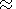 ln , and hence the characteristic
time of decay or growth of a two-vortex harmonic U10 j , are
less than the characteristic time of decay or growth of a
four-vortex harmonic U11 j by approximately a factor of 50.
ln , and hence the characteristic
time of decay or growth of a two-vortex harmonic U10 j , are
less than the characteristic time of decay or growth of a
four-vortex harmonic U11 j by approximately a factor of 50.
The solution of the problem of penetration of the electric field applied from the outside into the depth of the magnetosphere shows that this field can penetrate only if it sufficiently rapidly varies with time (the situation inverse to the skin effect). The charge separation resulting from the magnetic drift of particles leads to formation of the current system of region II and efficient screening of the inner magnetosphere. The development of instability must lead to disappearance of the disturbance which caused it, i.e., of the region of pressure growing with increasing radial distance. By creating the quasi-stationary azimuthally asymmetric distribution, the quasi-stationary dawn-dusk field will maintain the current system of region II which effectively screens its influence on the inner magnetosphere.
The azimuthally asymmetric plasma distribution itself can be
unstable.
Ivanov and Pokhotelov [1987]
analyzed the stability of
such a distribution with respect to development of short-wave flute
modes. It was shown that if the criterion for an ordinary flute
instability (5) is not satisfied, then for a flute instability with
a variable pressure on the surfaces of equal specific volumes under
the condition of maximum increment to arise, it is necessary that
the magnitude of the field-aligned current, i.e., 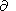 p0/
p0/ 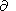 j , exceed
a certain threshold value.
Antonova [1993]
analyzed the development
of this instability taking into account a possible
nonequipotentiality of magnetic field lines. It was shown that
taking due account of nonequipotentiality owing to which the field
amplitudes in the magnetosphere can significantly exceed the field
amplitudes at ionospheric altitudes leads to an appreciable increase
in increments in the regions of outflowing field-aligned currents.
The maximum increments in this case will correspond to the regions
of maximum outflowing field-aligned current. Unfortunately, the
analysis of stability of the hot magnetospheric plasma distribution
is mostly restricted at present to the regions of low plasma
parameters b . The development of ballooning modes at finite b in the short-wave approximation was analyzed by
Ivanov et al. [1992].
j , exceed
a certain threshold value.
Antonova [1993]
analyzed the development
of this instability taking into account a possible
nonequipotentiality of magnetic field lines. It was shown that
taking due account of nonequipotentiality owing to which the field
amplitudes in the magnetosphere can significantly exceed the field
amplitudes at ionospheric altitudes leads to an appreciable increase
in increments in the regions of outflowing field-aligned currents.
The maximum increments in this case will correspond to the regions
of maximum outflowing field-aligned current. Unfortunately, the
analysis of stability of the hot magnetospheric plasma distribution
is mostly restricted at present to the regions of low plasma
parameters b . The development of ballooning modes at finite b in the short-wave approximation was analyzed by
Ivanov et al. [1992].
The possibility of generation of small-scale harmonics and nonequipotentiality of magnetic field lines for the scale of less than 200 km in the projection on ionospheric altitudes noticeably complicates the analysis of magnetosphere-ionosphere coupling because the nonequipotentiality of disturbances leads to the exchange of particles between magnetic field tubes. As a result of interaction between harmonics and energy exchange, a cascade process can arise in the turbulence spectrum and a quasi-stationary equilibrium turbulence spectrum will be formed, for which the dawn-dusk field will be the major large-scale energy source and dissipation will occur due to both heating of the ionospheric plasma during the flow of transverse currents which close the field-aligned currents in the ionosphere and absorption of the wave with transverse scales close to the Larmor radius of a hot magnetospheric ion. Plasma heating in the plasma sheet up to the temperatures exceeding the temperatures of particles in boundary layers can be associated with the latter process. These processes are still incompletely studied theoretically and experimentally. Weimer et al. [1985] and Basu et al. [1988] showed that expansion of the electric field measurements at low altitudes in the Fourier series give the Kolmogorov spectrum of the transverse electric field fluctuations
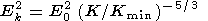 | (6) |
 Measurements by the DE 1 satellite at an altitude of 12,000 km
yielded
Measurements by the DE 1 satellite at an altitude of 12,000 km
yielded
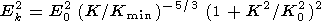 | (7) |
i.e., a growth of the fluctuation amplitude with decreasing
wavelength to the scales of the order of the Larmor radius of a hot
magnetospheric ion ( 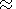 10 km in the projection onto the
ionospheric altitudes). Determination of the plasma velocities in
the plasma sheet at geocentric distances from 16 to 19 RE from
measurements of particle fluxes by ISEE and AMPTE/IRM satellites
[ Angelopoulos et al., 1993]
showed that the stochastic velocity
component is an order of magnitude greater than the regular
component. The existence of electric field fluctuations in the tail
exceeding by more than an order of magnitude the field fluctuations
at ionospheric altitudes (in the case of corresponding projection)
is well known from measurements in the tail
[ Scarf et al., 1984]
and
on auroral field lines
[ Mozer et al., 1980].
On the whole, the flow
pattern corresponds to the superposition of vortices of different
scales (Figure 4). Thus, as shown by
Antonova [1985], the
experimental observations speak in favor of the action of effective
mechanisms of diffusion intermixing. Indirect evidence of the action
of these mechanisms can be provided by a relatively weak dependence
of the plasma concentration and temperature on the radial distance.
For instance, checking of the relation between the field-aligned
current and field-aligned pressure drop in the inverted V type
structures indicates that j* is constant. In the AMPTE/CCE
experiment
[ Lui and Hamilton, 1992],
the plasma concentration was
independent of radial distance for 6 < L < 9 . Invariability of the
ionic temperature with latitude was noticed by
Antonova et al. [1991]
while analyzing the Intercosmos-Bulgaria 1300 satellite
measurements. The data of
Huang and Frank [1994]
also point to the
isothermal nature of the central part of the plasma sheet. The
question about the magnitude of the polytropic index g which is
used in the hydrodynamic description of the large-scale convection
is closely connected with the problem of intermixing in the plasma
sheet. The attempts to infer its magnitude from the experimental
measurements did not give an unambiguous result. For instance, while
studying the correlation between concentration and pressure,
Baumjohann and Pachmann [1989]
obtained gp close to 5/3 , and
Huang et al. [1989b]
obtained gT < 1 in the studies of
correlation between temperature and concentration.
Zhu [1990]
reported that
10 km in the projection onto the
ionospheric altitudes). Determination of the plasma velocities in
the plasma sheet at geocentric distances from 16 to 19 RE from
measurements of particle fluxes by ISEE and AMPTE/IRM satellites
[ Angelopoulos et al., 1993]
showed that the stochastic velocity
component is an order of magnitude greater than the regular
component. The existence of electric field fluctuations in the tail
exceeding by more than an order of magnitude the field fluctuations
at ionospheric altitudes (in the case of corresponding projection)
is well known from measurements in the tail
[ Scarf et al., 1984]
and
on auroral field lines
[ Mozer et al., 1980].
On the whole, the flow
pattern corresponds to the superposition of vortices of different
scales (Figure 4). Thus, as shown by
Antonova [1985], the
experimental observations speak in favor of the action of effective
mechanisms of diffusion intermixing. Indirect evidence of the action
of these mechanisms can be provided by a relatively weak dependence
of the plasma concentration and temperature on the radial distance.
For instance, checking of the relation between the field-aligned
current and field-aligned pressure drop in the inverted V type
structures indicates that j* is constant. In the AMPTE/CCE
experiment
[ Lui and Hamilton, 1992],
the plasma concentration was
independent of radial distance for 6 < L < 9 . Invariability of the
ionic temperature with latitude was noticed by
Antonova et al. [1991]
while analyzing the Intercosmos-Bulgaria 1300 satellite
measurements. The data of
Huang and Frank [1994]
also point to the
isothermal nature of the central part of the plasma sheet. The
question about the magnitude of the polytropic index g which is
used in the hydrodynamic description of the large-scale convection
is closely connected with the problem of intermixing in the plasma
sheet. The attempts to infer its magnitude from the experimental
measurements did not give an unambiguous result. For instance, while
studying the correlation between concentration and pressure,
Baumjohann and Pachmann [1989]
obtained gp close to 5/3 , and
Huang et al. [1989b]
obtained gT < 1 in the studies of
correlation between temperature and concentration.
Zhu [1990]
reported that
Since g = 1 corresponds to the isothermal distribution, the results of determination of g are also likely to provide evidence of the action of intermixing processes. The attempt to take into account theoretically the influence of irregular particle fluxes on the solution of the large-scale convection problem was made by Antonova [1987]; however, this aspect of the problem requires further investigation.
The possibility of the existence of quasi-equilibrium convection flows in the Earth's magnetosphere encounters the problem of "convection crisis" raised by Erickson and Wolf [1980]. The fact is that if the number of particles in the magnetic field tube is conserved and the tube moves toward the Earth from distant tail regions, the plasma pressure in the tube must increase extremely rapidly, which is not consistent with the experimental data. Consideration of the equilibrium plasma distribution in the magnetospheric tail led Schindler and Birn [1982], Birn and Schindler [1983], and Schindler and Birn [1986] to the conclusion that time-independent solutions of the equilibrium equation (in the two-dimensional case, the Grad-Shafranov equation) cannot exist. The time-dependent solutions with W = W(t) due to a decrease in the vertical field component in the plasma sheet during convection were obtained. This evolution of the configuration leads to thinning of the plasma sheet, with the final stage being formation of the tearing-type instability. However, in the experiment, the steady state convection regime is detected, though rarely [ Sergeev et al., 1994]. When solving the problem, Kivelson and Spence [1988] and Ashour-Abdalla et al. [1994] assumed that the number of particles in the tube is not conserved due to magnetic drift. In view of development of turbulent fluctuations, the problem of the "convection crisis" loses its importance because the concentration gradients arising during convection will decrease due to diffusion. Since the motion in the plasma sheet is directed toward the Earth, i.e., toward concentration increase, equilibrium between regular and diffusion flows is possible
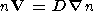 | (8) |
where V is the regular velocity, and D is the diffusion coefficient. If condition (8) is satisfied, the steady state plasma distribution is possible. The problems of particle heating during turbulence energy dissipation require separate consideration.
Analysis of the experimental observational data and theoretical approaches to the description of the magnetospheric convection shows that the generation of large-scale field-aligned currents and electric fields in the magnetospheric cavity results from the presence of pressure gradients along the equal volume isosurfaces of the magnetic tube. The action of this mechanism manifests itself in the geometry of the magnetospheric cavity at high latitudes and can be revealed by analyzing the profiles of isolines of equal volume and current lines in the equatorial plane. For the Earth's magnetosphere, the former have a larger curvature than the latter, which corresponds to the generation of currents entering the magnetosphere on the dawnside and flowing from it on the duskside and to the appearance of the large-scale electric field directed from the dawn toward dusk.
The presence of this field sustains the existence of the plasma sheet in the magnetospheric tail. The effect of the IMF on the field magnitude in this mechanism is due to changes in the currents on the magnetopause and inside the magnetosphere due to variations in IMF. The morning-evening field gives rise to an azimuthal pressure gradient in the region of dipole field lines with the maximum near the midnight, which provides the appearance of the currents of region II and of effective screening of the inner magnetosphere. The solution of the linear stationary problem of convection does not describe the location of maxima of currents of region II and the azimuthal electric field distribution at low latitudes.
The solution of the nonstationary linear problem allows us to determine the positions of the currents of region II being formed and localization of the convection electric fields and to estimate the characteristic times of growth of the morning-evening field and Alfv\'en screening.
In addition to large-scale fields, medium- and small-scale fields can be generated, and the spectrum of low-frequency turbulence leads to diffusion and variability in the number of particles in the magnetic field tube due to nonequipotential field lines. Taking into account the processes discussed leads to reconsideration of a number of commonly accepted concepts in the physics of magnetospheric plasma and helps in better explaining the experimental observational data.
The equation for continuity of the current integrated over the dynamo layer thickness is given by
 | (A1) |
where I is the magnetic declination, j ,
for which |dF
,
for which |dF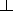 i|
i| 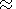 |E
|E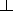 i|d
i|d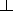
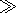 |dF||i|
|dF||i| 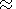 |E||| h ,
where h is the
dynamo layer thickness, dF
|E||| h ,
where h is the
dynamo layer thickness, dF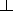 and dF
and dF
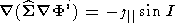 | (A2) |
where
 |
In the spherical coordinate system ( q is the colatitude and j is the azimuthal angle)
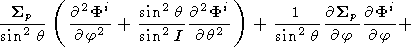 |
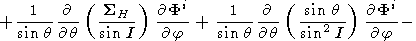 |
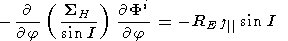 | (A3) |
In the high-latitude approximation, q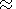 q, I = 1
q, I = 1
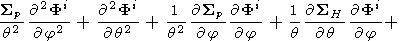 |
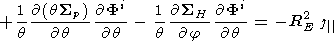 | (A4) |
If Sp, SH = const
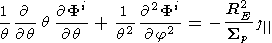 | (A5) |
At the equatorial boundary, in the case of symmetry of hemispheres,
the boundary condition is J
In solving the problem of magnetosphere-ionosphere coupling, it is convenient to use Eulerian potentials ( a, , b )
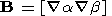 | (B1) |
In the dipole magnetic field a = - B0 RE2sin2 q /r , b = RE j , where B0 = -0.308 G is the field at the equator, and r is the geocentric distance.
In case of conservation of the first and second adiabatic invariant, the dependence of the distribution function f(a, b, m, J, t ) on the Hamiltonian H(a, b, m, J, t ) is given by [ Pellat and Laval, 1972]
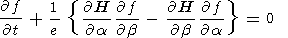 | (B2) |
For equipotential magnetic field lines
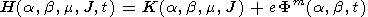 | (B3) |
The equation for continuity of cold electrons of the magnetosphere on the assumption of nondivergence of the ion current is
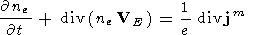 | (B4) |
which gives on integration over the magnetic field tube
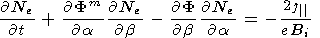 | (B5) |
where Ne (a, b, t) = ne di/B =N is the number of electrons in the magnetic field tube with a unit flux and Bi is the magnetic field in the ionosphere. The factor of 2 is associated with the existence of two conjugated hemispheres. From (B2) and (B5) we obtain
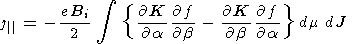 | (B6) |
If eFm is regarded as a small disturbance of the Hamiltonian, the linear solutions for (B2) can be found
By designating the azimuthal drift velocity through wd (a, m, J) = (1/eRE)(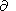 K/
K/ 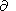 a) , we
obtain
a) , we
obtain
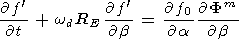 |
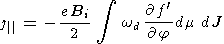 | (B7) |
From (B7), for 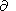 /
/ 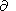 t=0 , it follows that
t=0 , it follows that
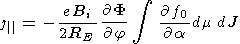 | (B8) |
and for the characteristic times of the process t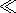 w
w
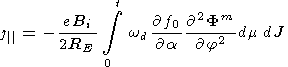 | (B9) |
On the assumption that the main contribution to the magnetospheric
pressure comes from slowly moving ions, i.e., pe 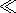 pi = p (pe
pi = p (pe 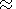 0.1pi in the plasma sheet) and the plasma velocity is | v|
0.1pi in the plasma sheet) and the plasma velocity is | v| 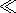 vA, vs where vA and vs are the Alfv\'en and sound velocities,
respectively, the velocities of electrons ve and ions vi are
determined from (quasi-neutrality is assumed)
vA, vs where vA and vs are the Alfv\'en and sound velocities,
respectively, the velocities of electrons ve and ions vi are
determined from (quasi-neutrality is assumed)
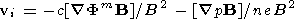 | (C1) |
where Fm is the potential in the magnetosphere. In what follows we use Fm = F (a, b, t) , i.e., we assume that the magnetic field lines are equipotential. The equation for energy transfer is written as
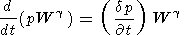 | (C2) |
where g = 5/3 is the index of the adiabat, W = di/B is the magnetic field tube volume, and the term in the right-hand part sums up the sources and "sinks" of the plasma pressure (injection of ions from the ionosphere and ejection into the ionosphere, heat flows, etc.). For simplicity, we take (dp/ dt) = 0 , and take into account the possibility of nonadiabatic processes by introducing g different from 5/3 .
Using the Eulerian potentials, we take W = W(a) , and then
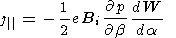 | (C3) |
where Bi is the magnetic field at the ionospheric altitudes. In the linear approximation
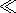 p0
p0 From (C1) and (C2) with the right-hand side equal to zero, it follows that
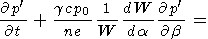 |
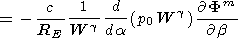 | (C4) |
By introducing the hydrodynamic analog of the magnetic drift frequency
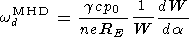 |
we obtain
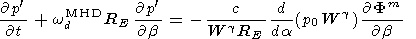 | (C5) |
Equations (C3) and (C5) predict the relation of the
field-aligned current with the disturbance of the potential. In the
stationary case 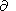 /
/ 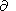 t = 0 ,
by introducing the number of
particles in the magnetic field tube N0 = p0W/T0 , we obtain
t = 0 ,
by introducing the number of
particles in the magnetic field tube N0 = p0W/T0 , we obtain
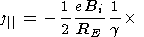 |
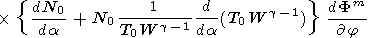 | (C6) |
In the nonstationary case, for the characteristic times of the
process t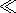 (wd MHD)
(wd MHD)
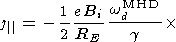 |
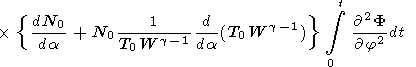 | (C7) |
In the dipole field in the high-latitude approximation at g = 1 , by equating (A4) and (C6) at Fi = Fm = F , we obtain the equation for convection in the form
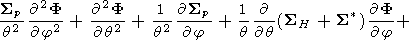 |
 | (C8) |
where S* = (1/2) e N0 is the "magnetospheric conductivity".
Angelopoulos, V., et al., Characteristics of ion flow in the quiet state of the inner plasma sheet, Geophys. Res. Lett., 20 (16), 1711, 1993.
Antonova, E. E., Magnetic mirror particle reflection and electrostatic fields in space, Phys. Solaritter Potsdam, 24, 5, 1984.
Antonova, E. E., On nonadiabatic diffusion, and equalization of concentration and temperature in the plasma sheet of the Earth's magnetosphere, Geomagn. Aeron., 25 (4), 623, 1985.
Antonova, E. E., On the problem of fundamental harmonics in the magnetospheric turbulence spectrum, Phys. Scr., 35 (6), 880, 1987.
Antonova, E. E., The development of initial substorm expansive phase disturbance due to generation of localized electric fields in the region of maximum upward field-aligned current, Adv. Space Res., 13 (4), 261, 1993.
Antonova, E. E., and N. Yu. Ganyushkina, On the choice of the coordinate system for description of magnetostatically equilibrium regions in the magnetosphere, Geomagn. Aeron., 34 (4), 58, 1994.
Antonova, E. E., and N. Yu. Ganyushkina, Geometry of the magnetic field of the Earth's magnetosphere and generation of field-aligned currents, Geomagn. Aeron., 35 (5), 9, 1995a.
Antonova, E. E., and N. Yu. Ganyushkina, On the influence of the interplanetary magnetic field on generation of large-scale field-aligned currents, Geomagn. Aeron., 35 (6), 32, 1995b.
Antonova, E. E., and N. Yu. Ganyushkina, Recovery of large-scale azimuthal pressure gradients in the magnetosphere from the data on field-aligned currents, Geomagn. Aeron., 35 (5), 16, 1995c.
Antonova, E. E., and B. A. Tverskoy, On the nature of the electron precipitation band of the inverted V type and the Harang discontinuity in the evening sector of the auroral ionosphere, Geomagn. Aeron., 15 (1), 105, 1975.
Antonova, E. E., and B. A. Tverskoy, The formation of magnetospheric turbulence spectrum and the magnetospheric substorm theory, Issled. Geomagn. Aeron. Fiz. Solntsa, 89, 199, 1990.
Antonova, E. E., N. Yu. Ganyushkina, A. A. Gusev, and G. I. Pugacheva, Shapes of the isolines of equal volume of magnetic field tubes and the problem of choice of the coordinate system for description of the processes at high latitudes, Geomagn. Aeron., 33 (3), 59, 1993.
Antonova, E. E., et al., Parameters of multiplet inverted V type structures from the data of Intercosmos-Bulgaria satellite, Geomagn. Aeron., 31 (2), 258, 1991.
Ashour-Abdalla, M., L. N. Zelenyi, and V. Perroomian, On the structure of the magnetotail current sheet, Geophys. Res. Lett., 20 (19), 2019, 1993.
Ashour-Abdalla, M., L. N. Zelenyi, V. Perroomian, and \linebreak R. L. Richard, Consequences of magnetotail ion dynamics, J. Geophys. Res., 99 (A8), 14,891, 1994.
Basu, Sananda, et al., Simultaneous density and electric field fluctuation spectra associated with velocity shears in the auroral oval, J. Geophys. Res., 93 (A1), 115, 1988.
Baumjohann, W., and G. Pachmann, Determination of the polytropic index in the plasma sheet, Geophys. Res. Lett., 16 (4), 295, 1989.
Bespalov, P. A., and V. Yu. Trachtengertz, Alfv\'en Mazers, 190 pp., Inst. Appl. Mech., Acad. Sci. USSR, Gorki, 1986.
Birn, J., and K. Schindler, Self-consistent theory of three-dimensional convection in the geomagnetic tail, J. Geophys. Res., 88 (A9), 6969, 1983.
Blanc, M., and G. Caudal, The spatial distribution of magnetospheric convection electric fields at ionospheric altitudes, 2, Theories, Ann. Geophys., 3 (1), 27, 1985.
Bosqued, J. M., C. Maurel, J. A. Sauvaud, et al., Observation of auroral electric inverted- V structures by the Aureol 3 satellite, Planet. Space Sci., 34 (3), 255, 1986.
Buchner, J., and L. M. Zelenyi, Regular and chaotic charged particle motion in magnetotaillike field reversals, 1, Basic theory of trapped motion, J. Geophys. Res., 94 (A9), 11,821, 1989.
Chen, J., and P. J. Palmadesso, Chaos and nonlinear dynamics: Single-particle orbits in a magnetotaillike magnetic field, J. Geophys. Res., 91, 1499, 1986.
Chen, C. K., R. A. Wolf, M. Harel, and J. L. Karty, Theoretical magnetograms based on quantitative simulation of a magnetospheric substorm, J. Geophys. Res., 87 (A8), 6137, 1982.
Christon, S. P., L. A. Frank, C. Y. Huang, et al., Spectral characteristics of plasma sheet ion and electron populations during disturbed geomagnetic conditions, J. Geophys. Res., 96 (A1), 1, 1991.
Del Pozo, C. F., and M. Blanc, Analytical self-consistent model of the large-scale convection electric field, J. Geophys. Res., 99 (A3), 4053, 1994.
Elphinstone, R. D., D. Hearn, J. S. Murphree, and L. L. Cogger, Mapping using the Tsyganenko long magnetospheric model and its relationship to Viking auroral images, J. Geophys. Res., 96 (A2), 1467, 1991.
Erickson, G. M., and R. A. Wolf, Is the steady convection possible in the Earth's magnetotail?, Geophys. Res. Lett., 7 (11), 897, 1980.
Fairfield, D. H., Solar wind control of the distant magnetotail: ISEE 3, J. Geophys. Res., 98 (A12), 21,265, 1993.
Feldstein, Ya. I., and Yu. I. Galperin, The auroral luminosity structure in the high-latitude upper atmosphere: Its dynamics and relationship the large-scale structure of the Earth's magnetosphere, Rev. Geophys., 23 (3), 217, 1985.
Foster, J. C., T. Fuller-Rowell, and D. S. Evans, Quantitative patterns of large scale field-aligned currents in the auroral ionosphere, J. Geophys. Res., 94, 2555, 1989.
Frank, L. A., et al., The theta aurora, J. Geophys. Res., 91 (A3), 3177, 1986.
Galperin, Yu. I., and Ya. I. Feldstein, Auroral luminosity and its relationship to magnetospheric plasma domains, Preprint Pr.-1566, 50 pp., IKI Acad. Sci. USSR, Moscow, 1989.
Harel, M., et al., Quantitative simulation of a magnetospheric substorm, 1, Model logic and overview, J. Geophys. Res., 86 (A4), 2217, 1981a.
Harel, M., et al., Quantitative simulation of a magnetospheric substorm, 2, Comparison with observations, J. Geophys. Res., 86 (A4), 2242, 1981b.
Huang, C. Y., and L. A. Frank, A statistical survey of central plasma sheet, J. Geophys. Res., 99 (A1), 83, 1994.
Huang, C. Y., J. D. Craven, and L. A. Frank, Simultaneous observations of a theta aurora and associated magnetotail plasma, J. Geophys. Res., 94 (A8), 10137, 1989a.
Huang, C. Y., C. K. Goertz, L. A. Frank, and G. Rostoker, Observational determination of the adiabatic index in the quiet time plasma sheet, Geophys. Res. Lett., 16 (6), 563, 1989b.
Iijima, T., and T. A. Potemra, The amplitude distribution of the field-aligned currents at northern high latitudes observed by Triad, J. Geophys. Res., 81 (13), 2165, 1976.
Ivanov, V. N., and O. A. Pokhotelov, Flute instability in the plasma sheet of the Earth's magnetosphere, Fiz. Plazmy, 13 (11), 1446, 1987.
Ivanov, V. N., et al., Ballooning instability in the Earth's magnetosphere at variable and finite pressure, Geomagn. Aeron., 32 (2), 68, 1992.
\small
Johnson, F. S., The driving force for magnetospheric convection, Rev. Geophys., 16 (2), 161, 1978.
Kadomtsev, B. B., Hydromagnetic Stability of Plasma, in Problems of Plasma Theory, edited by M. A. Leontovich, p. 132, Moscow, 1963.
Karty, J. L., R. A. Wolf, and D. W. Spiro, Region one Birkeland currents connecting to sunward convecting flux tubes, in Magnetospheric Currents, edited by T. A. Potemra, pp. 269-275, AGU, Washington, D.C., 1984.
Kennel, C. F., Limit of stable trapped particle fluxes, J. Geophys. Res., 71 (1), 1, 1966.
Kivelson, M. G., and H. E. Spence, On the possibility of quasi-static convection in the quiet magnetotail, Geophys. Res. Lett., 15 (13), 1541, 1988.
Knight, S., Parallel electric fields, Planet. Space Sci., 21 (5), 741, 1973.
Lindqvist, P. A., and F. S. Mozer, The average tangential electric field and the noon magnetopause, J. Geophys. Res., 95 (A10), 17,137, 1990.
Lui, A. T. Y., and D. C. Hamilton, Radial profiles of quiet time magnetospheric parameters, J. Geophys. Res., 97 \linebreak (A12), 19,325, 1992.
Lui, A. T. Y., R. W. McEntire, and S. M. Krimigis, Evolution of the ring current during two geomagnetic storms, J. Geophys. Res., 92 (A7), 7459, 1987.
Lundin, R., On the magnetospheric boundary layer and solar wind energy transfer into the magnetopause, Space Sci. Rev., 48 (3-4), 263, 1988.
Lyatskiy, V. B., Current Systems of Magnetosphere-Ionosphere Disturbances, 198 pp., Nauka, St. Petersburg, 1978.
Lyons, L. R., Discrete aurora as the direct result of an inferred high altitude generating potential distribution, J. Geophys. Res., 86 (1), 1, 1981.
Lyons, L. R., and D. J. Williams, Quantitative Aspects of Magnetospheric Physics, 312 pp., D. Reidel, Hingham, Mass., 1984.
Maynard, N. C., J. P. Heppner, and T. L. Aggson, Turbulent electric fields in the nightside magnetosphere, J. Geophys. Res., 87 (A3), 1445, 1982.
Mozer, F. S., et al., Satellite measurements and theories of low altitude auroral particle acceleration, Space Sci. Rev., 27 (1), 155, 1980.
Pellat, R., and G. Laval, Remarks of the steady and time dependent mathematical convection models, in Critical Problems of Magnetospheric Physics, edited by E. R. Dyer, p. 237, IUCSTP, Washington, D. C., 1972.
Peredo, M., D. P. Stern, and N. A. Tsyganenko, Are existing magnetospheric models excessively stretched?, J. Geophys. Res., 98 (A9), 15,343, 1993.
Petersen, A., et al., Electric fields in the plasma sheet and plasma sheet boundary layer, J. Geophys. Res., 87 (A3), 1445, 1982.
Peymiat, C., and D. Fontaine, Numerical simulation of magnetospheric convection including the effect of field-aligned currents and electron precipitation, J. Geophys. Res., 99 (A6), 11,155, 1994.
Pudovkin, M. I., and V. E. Zakharov, Numerical simulation of magnetosphere-ionosphere coupling, including kinetic effects in the plasma sheet, Planet. Space Sci., 40 (8), 1071, 1992.
\small
Saunders, M., Magnetosheath, magnetopause, and low latitude boundary layer research, J. Atmos. Terr. Phys., 52, 1107, 1990.
Scarf, F. L., et al., ISEE wave measurements in the distant geomagnetic tail and boundary layer, Geophys. Res. Lett., 11 (4), 335, 1984.
Schindler, K., and J. Birn, Self-consistent theory of time-dependent convection in the Earth's magnetotail, J. Geophys. Res., 87 (A4), 2263, 1982.
Schindler, K., and J. Birn, Magnetotail theory, Space Sci. Rev., 44 (1-2), 307, 1986.
Sergeev, V. A., T. I. Pulkkinen, R. J. Pellinen, and N. A. Tsyganenko, Hybrid state of the tail magnetic configuration during steady convection events, J. Geophys. Res., 99 (A12), 23,571, 1994.
Shabanskiy, V. P., Phenomena in the Near-Earth Space, 271 pp., Nauka, Moscow, 1972.
Sibeck, D. G., R. E. Lopes, and E. C. Roelof, Solar wind control of the magnetopause shape, location, and motion, J. Geophys. Res., 96 (A4), 5489, 1991.
Song, P., and C. T. Russell, Model of the formation of the low-latitude boundary layer for strongly northward interplanetary magnetic field, J. Geophys. Res., 97 (A2), 1411, 1992.
Song, P., et al., Structure and properties of the subsolar magnetopause for northward interplanetary magnetic field: Multiple-instrument particle observations, J. Geophys. Res., 98 (A7), 11,319, 1993.
Sonnerup, B. U. O., I. Papamastorakis, G. Pashman, and H. Luhr, The magnetopause for large magnetic shear: Analysis of convection electric fields from AMPTE/IRM, J. Geophys. Res., 95 (A7), 10,541, 1990.
Spiro, R. W., M. Harel, R. A. Wolf, and P. H. Reiff, Quantitative simulation of a magnetospheric substorm, 3, Plasmaspheric electric fields and evolution of the plasmapause, J. Geophys. Res., 86 (A4), 2261, 1981.
Stern, D. P., The origins of Birkeland Currents, Rev. Geophys., 21 (1), 125, 1983.
Stern, D. P., The linkage between the ionosphere and the plasma sheet, J. Geomagn. Geoelectr., 44, 1109, 1992.
Stiles, G. S., E. W. Hones, J. S. Bame, and J. R. Asbridge, Plasma sheet pressure anisotropies, J. Geophys. Res., 83 (3), 3166, 1978.
Tsyganenko, N. A., Global quantitative models of the geomagnetic
field in the cislunar magnetosphere for different\refparbreak
Tsyganenko, N. A., Quantitative models of the magnetospheric magnetic field: Methods and results, Space Sci. Rev., 54 (1-2), 75, 1990.
Tsyganenko, N. A., and D. G. Sibeck, Concerning flux erosion from the dayside magnetosphere, J. Geophys. Res., 99 (A7), 13,425, 1994.
Tverskoy, B. A., On electric fields in the Earth's magnetosphere, Dokl. Akad. Nauk SSSR, 188 (3), 575, 1969.
Tverskoy, B. A., Electric fields in the magnetosphere and the origin of trapped radiation, in Solar-Terrestrial Physics, edited by E. R. Dyer, part III, p. 297, Dordrecht, Hingham, Mass., 1972.
Tverskoy, B. A., On the field-aligned currents in the magnetosphere, Geomagn. Aeron., 22 (6), 991, 1982.
Tverskoy, B. A., Magnetosphere-ionosphere coupling and auroras, Usp. Fiz. Nauk, 139 (4), 737, 1983.
Vasyliunas, V. M., Mathematical models of magnetospheric convection and its coupling to the ionosphere, in Particles and Fields in the Magnetosphere, edited by B. M. McCormac, pp. 60-71, Dordrecht, Hingham, Mass., 1970.
Vasyliunas, V. M., The interrelationship of magnetospheric processes, in Solar-Terrestrial Physics, edited by E. R. Dyer, p. 29, Dordrecht, Hingham, Mass., 1972.
Walker, R. J., and T. Ogino, Global magnetohydrodynamic simulations of the magnetosphere, ISEE Trans. Plasma Sci., 17 (2), 135, 1989.
Watanabe, K., and T. Sato, Global simulation of the solar wind magnetosphere interaction: The importance of its numerical validity, J. Geophys. Res., 95 (A1), 75, 1990.
Weimer, D. R., et al., Auroral zone electric fields from DE 1 and 2 at magnetic conjunctions, J. Geophys. Res., 90 (A8), 7479, 1985.
Wolf, R. A., et al., Computer simulation of inner magnetospheric dynamics for the magnetic storm of July 29, 1977, J. Geophys. Res., 87 (A8), 5949, 1982.
Yang, Y. S., R. W. Spiro, and R. A. Wolf, Generation of region-I current by magnetospheric pressure gradients, J. Geophys. Res., 99 (A1), 223, 1994.
Zhu, X. M., Plasma sheet polytropic index as inferred from the FPE measurements, Geophys. Res. Lett., 17 (12), 2321, 1990.