Rate of proton intensity decay in solar cosmic ray events as...

4. Dependence of τ on the Energy of Protons

Figure 2

[12] The time of the first arrival of particles after the flare to the point of observation and the time of the flux growth up to its maximal value in the overwhelming majority of events decreases with an increase of the particle energy. The energy dependence of the rate of decays in solar energetic particle (SEP) events is not so definite. Besides the events in which τ decreases with an energy growth, the cases with inverse dependence of τ on the energy, as well as the cases in which there is no dependence of τ on the energy are detected. Figure 2 shows the examples of different behavior of decays as a function of energy: the decay rate does not depend on energy (Figure 2a), it decreases with energy (Figure 2b), and the decay rate increases with energy (Figure 2c).

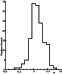
Figure 3

[13] For the investigation of this dependence, from the total amount of events with the exponential decay available to the authors (obtained by the instrument CPME on board IMP 8 for the period from 1974 to 2001), those events were selected for which it was possible to determine the characteristic decay time τ for protons with energies at least 15-25 MeV. In the channels <2 MeV, as a rule, particles accelerated near the observation point are present. In our analysis, these channels were excluded from the consideration. As it has been mentioned above, the total amount of 147 events was selected, where τ could be determined at least in 4 energy intervals. The value of n was determined for them from the functional form τ(E)=CE^-n, where E is the kinetic energy of protons and the values of exponent n were obtained from least squares fits. The usual statistical error of n was about 0.05. Figure 3 shows the distribution of values of n for all 147 events. One can consider this distribution as consisting of three different groups: (1) no τ dependence on proton energy ( -0.1 τ with energy ( n > 0.1; 72 events), and (3) an increase of τ with energy ( n < -0.1; 21 events). In the first case, the proton spectrum does not change with time during decay; in the second case the spectrum becomes softer; and in the third case it becomes harder. Thus, one can see that in the prevailing number of cases, τ either does not depend on the particle energy or decreases with an energy growth.

[14] It is worth noting that to our knowledge the energy dependence of the characteristic decay time τ has not been analyzed quantitatively before. Actually, the existence of decays with τ independent of particle energy was mentioned before [Daibog et al., 2000; Reames et al., 1997] in the so-called invariant events when in connection with the passage of the shock wave initiated by the coronal mass ejection (CME), the state of the interplanetary space provided equal rates of proton flux declines with different energies in different points of space situated far from each other. Unfortunately, this analysis was performed only for several selected events most of which, probably, were related to the trapping of accelerated particles between the front of a shock wave (associated with CME) and strong magnetic fields on the Sun. Strictly speaking, in this case the decay phase probably should be described (as it is the case in the diffusion model) by a power law but not by the exponential dependence [Reames et al., 1996].

[15] For the diffusion events, the rate of flux declines depends significantly on the energy: the higher the particle energy, the faster is the flux decline. It is quite natural because the density of particles after the maximum in the elementary diffusion approximation is proportional to (Dt)^-3/2, and the diffusion coefficient D = lv/3 grows with energy (here l is the mean free path related to the scattering at irregularities of the magnetic field, which is assumed to increase with energy, and v is the velocity of particles). Formally, the exponential decay with τ depending on the energy can be obtained in the diffusion models with absorbing boundary located at a finite distance R_abs [Forman, 1971, and references therein]. In this case, after the propagation of the crest of the diffusion wave up to the distance R_abs, the solution becomes exponential with τ=R_abs²/p² D [Dorman and Miroshnichenko, 1968]. The solution decreases with energy growth, but for D(r) = const it is independent of the parameters entering (1). However, τ depends statistically on all three parameters. So, the exponential form of the decay probably testifies that the main role belongs not to the diffusion but to the convective transport of particles and their adiabatic cooling, and in the case of exponential decays we could always expect τ to be independent of the particle energy. Therefore, the obtained result shows that probably in the case of exponential decays, in many events the influence of the diffusion becomes apparent only at the early stage of the propagation near the Sun.

[16] It is worth noting that generally speaking, the problem of the relation between the diffusion, convective, and adiabatic terms in the equation of particle transport is marked by some paradox. The exponential solution of the equation of particles transport was obtained by Forman [1970] and Jokipii [1972] assuming that one may neglect the diffusion of particles. However, it should be mentioned that convective transport and adiabatic cooling, in principle, are impossible without diffusion. Indeed, in the absence of scattering, particles cannot be captured by the solar wind. What does it mean that one may neglect the diffusion in comparison with other processes? Diffusion propagation is completely absent in two cases: (1) the diffusion coefficient D 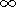infty (this is a free expansion, but if there is no scattering, neither convection nor adiabatic cooling can exist) and (2) the diffusion coefficient D 0. This means that in the absence of the solar wind, particles will remain in the place of their injection and their propagation in IS would not occur. The radial expansion of the solar wind provides in this case the convection and adiabatic cooling. Lee [2000] discussed the case of adiabatic cooling without convection and obtained a solution partly different from (1):

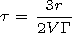(2)

where γ is the differential momentum spectral index. In principle, such a suggestion is non-contradictory if particles are contained in some expanding volume under absence of solar wind. In the presence of the solar wind, adiabatic cooling cannot exist without convection. Indeed, both these phenomena are consequences of the same process: the capture of particles by expanding solar wind (however, if the solar wind was present in the tube with a constant cross section, one-dimensional case, contrary to Lee [2000], the convection would exist without adiabatic cooling). Therefore, even with the dominating convection and adiabatic cooling, the diffusion always plays a certain role in particle propagation through the interplanetary space.

[17] Especially unexpected is the presence of the group of events with negative n, what cannot be explained by any of the three considered mechanisms of propagation. In this group, the growth of τ with the particle energy is observed almost for all values of τ: 5 < τ< 30 h. This means that the negative values of n are not a consequence of uncertainties related to the measurements (e.g., enhanced values of the background fluxes). We tried to find an explanation for these unusual decays as the influence of some additional particle source analyzing what effects shocks and shock particles might have on values of n. From 21 decays of this group, 10 were shock associated. Only 4 definitely looks as shock-influenced, 3 are doubtful. 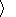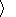For 11 decays without shocks langle n rangle = -0.17, for 10 shock related decays langle n rangle = -0.20. If extreme n = -0.48 is excluded, for other 9 decays langle n rangle = -0.17. Thus, both subgroups have nearly the same values of n and shocks could not be an explanation of existence of negative values of n and in spite of our earlier result that the presence of a shock statistically makes τ smaller [Daibog et al. 2003b], this small group of decays (21) does not demonstrate this feature. This result shows that there exist events with exponential declines, in which either additional mechanisms act that have not been taken into account by formula (1) or that such decays are formed by the joint action of parameters of IS with the corresponding dependence on the energy.

Figure 4

[18] Out of 147 events for which the value of n was determined, we managed to connect 104 events with flares, i.e. with the sources of particles on the Sun. For the protons with energies >4 MeV, Daibog et al. [2006] considered in detail the dependence of τ on heliolongitude of the flare. They showed that statistically τ does not depend on heliolongitude of the observer for events associated with flares occurring eastward from the optimum heliolongitude. At the same time, in the case of flares occurring westward, there exists a tendency of the decrease of τ with a growth of the angular distance between the flare and the point of observation. This manifests the influence of the solar rotation. The data available allow us to investigate the problem how τ depends on the heliolongitude of a flare for particles with different energies and consequently, the dependence of the exponent n that enters the law τ(E) = CE^-n, on the heliolongitude of a flare (a source of the particles). Figure 4 shows such dependence of n based on 104 events. One can see in Figure 4 that statistically there is no dependence of n on the heliolongitude of a flare. Concerning solar event intensities, this result shows that the transverse propagation of particles (coronal or interplanetary) can only slightly influence the energetic characteristics of the decline rate.