1. Introduction
[2] The time profile of particle fluxes in the solar events has a
typical shape with the more or less quick rise, the maximum,
and much slower decay towards the level before the flare. The
phase of decay contains important information on the physical
processes to which particles are subjected in the interplanetary
space. Different mechanisms of particle propagation lead to
different laws describing the decrease of fluxes at the late stage
of the event. Sometimes this picture can be presented in the
diffusion approximation. Then, within the elementary diffusion
model under the assumption of a pulsed source of particles and
the boundary condition
J(r) = 0 at
r = 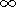 ( J is the flux of particles
and
r is the distance from the source), the time profile of fluxes
at the decay phase of the event has a power law shape and it is
proportional to
t-3/2, where
t is the time from the moment of the
injection of particles. In diffusion models with the absorbing
boundary situated at a finite distance from the source, the
decline of the intensity can be described by the exponential
function with the standard value of the characteristic decay time
which does not depend on the parameters of the surrounding
plasma and the spectrum of particles.
( J is the flux of particles
and
r is the distance from the source), the time profile of fluxes
at the decay phase of the event has a power law shape and it is
proportional to
t-3/2, where
t is the time from the moment of the
injection of particles. In diffusion models with the absorbing
boundary situated at a finite distance from the source, the
decline of the intensity can be described by the exponential
function with the standard value of the characteristic decay time
which does not depend on the parameters of the surrounding
plasma and the spectrum of particles.
[3] However, in the interplanetary space, the solar wind providing
the convective transport of particles and their adiabatic cooling
is usually present. If such processes prevail in comparison with
the diffusion, the fluxes decrease exponentially. Power law
intensity decrease can frequently be observed for high energies
(>50 MeV), while for smaller energies
 10 MeV, convective
transport and adiabatic cooling begin to play substantially
greater role and the decline of particle fluxes becomes
exponential
[Lee, 2000].
Thus, the very shape of the decay
contains certain information about the processes of particle
propagation in the interplanetary space. Moreover, the
dependence of the decay rate on different parameters clarifies
the role of three main mechanisms (diffusion, convection, and
adiabatic cooling) during the propagation from the source to the
point of observation. We discuss interrelation of the above
mechanisms in section 4. Our task is not the description of
particular solar energetic particle (SEP) events but the
elucidation of statistical regularities that characterize this phase
of the event.
10 MeV, convective
transport and adiabatic cooling begin to play substantially
greater role and the decline of particle fluxes becomes
exponential
[Lee, 2000].
Thus, the very shape of the decay
contains certain information about the processes of particle
propagation in the interplanetary space. Moreover, the
dependence of the decay rate on different parameters clarifies
the role of three main mechanisms (diffusion, convection, and
adiabatic cooling) during the propagation from the source to the
point of observation. We discuss interrelation of the above
mechanisms in section 4. Our task is not the description of
particular solar energetic particle (SEP) events but the
elucidation of statistical regularities that characterize this phase
of the event.
[4] It was shown in our previous papers that in about 90% of events
the fluxes of protons with low energies ( <10 MeV) have an
exponential decay while for particles with high energies
( >30-60 MeV) exponential decay is detected much more seldom. We
discussed in detail the mean values of
τ, as well as the
peculiarities of the characteristic decay time as a function of the
size of the event (distributions of
τ for protons with energies
E >4 MeV are practically the same for events with
J max > 100 (cm2 s sr)-1 and with
J max > 2-3 (cm2 s sr)-1 [Daibog et al., 2003a]),
parameters of the surrounding plasma (the solar wind velocity
and the magnetic field intensity
[Daibog et al., 2005a, 2005b]),
the angular distance between the source and the point of
observations, etc., and also variations of
τ during the solar
activity cycle
[Daibog et al., 2003b;
Kecskeméty et al., 2003].
[5] One can assume that if the decay of particle fluxes in the solar
event does not change its character for a long time (of the order
of a day or more), then the nearest interplanetary space (IS) is
homogeneous and quasi-stationary. This guarantees the
constancy of
τ in the case of the exponential decline. The
statement that the IS is quasi-stationary assumes the invariance
of the whole complex of its properties. They are the following:
(1) gradient of the particle density in the vicinity of the
observation point and the velocity (determined by the diffusion
coefficient of particles and their convective outflow) with which
particles leave the given region of space, (2) adiabatic cooling of
particles in the process of propagation, and (3) possible
acceleration of particles in the vicinity of the point of
observation. The relative contribution of each of these processes
into the formation of a time profile varies in different events.
That is why we have to discuss the whole complex of processes
what results in the exponential decrease of particle fluxes during
an extended period (sometimes up to several days). One can
describe this decrease rather strictly by the exponential law with
a constant characteristic time
τ. The numerical value of
τ is the
generalized characteristic of the action of space on the time
profile of particle fluxes. The investigation of the role of each
component of such action is one of the tasks of the
interplanetary space exploration. In this paper we investigate the
dependences of the characteristic time of proton fluxes decay
τ in the events with the exponential decrease as functions of the
solar wind velocity, the index of the energetic spectrum, and
also the energy of particles. These dependences make it possible
to observe the action of the main mechanisms that determine to
a considerable extent the value of
τ.
[6] It follows from the most general considerations that if the
convective transport of particles by the solar wind takes place,
τ should decrease with a growth of the solar wind speed
V. If the
adiabatic cooling of particles takes place, the rate of decline
should increase due to the falling particle spectrum
J(E)  E-γ and
τ diminishes with a growth of the spectral index
γ. With the
increase of the distance
r from the source,
τ grows because it
requires more time for particles localized in a larger volume to
outflow from this volume.
E-γ and
τ diminishes with a growth of the spectral index
γ. With the
increase of the distance
r from the source,
τ grows because it
requires more time for particles localized in a larger volume to
outflow from this volume.
[7] Forman [1970]
and Jokipii [1972]
showed that if the convective
transport and adiabatic cooling dominate over the diffusion
during the decay stage, the temporal profile of particle fluxes is
described by the dependence
J(t)  exp(-t/τ). They obtained
analytically an expression for the characteristic decay time
τ taking into account the dependences on all three parameters
r,
V,
and
γ:
exp(-t/τ). They obtained
analytically an expression for the characteristic decay time
τ taking into account the dependences on all three parameters
r,
V,
and
γ:
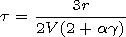 | (1) |
where
a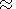 2 for nonrelativistic particles. As far as we consider in
this paper measurements conducted on IMP 8, we shall not
touch the
τ dependence on the distance from the source,
assuming the Sun to be always such a source. It should be
mentioned that
Kecskeméty et al. [2005]
showed that on the
basis of the currently existing simultaneous measurements in
high energy channels on board Ulysses (3-5 AU) and IMP 8 (in
these measurements 49 events of the solar cosmic rays (SCR) on
Ulysses were identified reliably with the events at 1 AU) the rate
of proton fluxes decline both at low (4-5 MeV) and high
( >30 MeV) energies at 1 AU is always higher than at 3-5 AU.
However, for several events the time profiles for protons with
energies
>30 MeV on IMP 8 and on Ulysses coincided
[McKibben et al., 2001, 2003].
For the explanation of this
phenomenon, these authors used the proposed earlier model of
"the homogeneous reservoir of particles"
[McKibben, 1972;
Roelof et al., 1992].
This, however, does not change the general
picture.
2 for nonrelativistic particles. As far as we consider in
this paper measurements conducted on IMP 8, we shall not
touch the
τ dependence on the distance from the source,
assuming the Sun to be always such a source. It should be
mentioned that
Kecskeméty et al. [2005]
showed that on the
basis of the currently existing simultaneous measurements in
high energy channels on board Ulysses (3-5 AU) and IMP 8 (in
these measurements 49 events of the solar cosmic rays (SCR) on
Ulysses were identified reliably with the events at 1 AU) the rate
of proton fluxes decline both at low (4-5 MeV) and high
( >30 MeV) energies at 1 AU is always higher than at 3-5 AU.
However, for several events the time profiles for protons with
energies
>30 MeV on IMP 8 and on Ulysses coincided
[McKibben et al., 2001, 2003].
For the explanation of this
phenomenon, these authors used the proposed earlier model of
"the homogeneous reservoir of particles"
[McKibben, 1972;
Roelof et al., 1992].
This, however, does not change the general
picture.

Powered by TeXWeb (Win32, v.2.0).
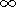 ( J is the flux of particles
and
r is the distance from the source), the time profile of fluxes
at the decay phase of the event has a power law shape and it is
proportional to
t-3/2, where
t is the time from the moment of the
injection of particles. In diffusion models with the absorbing
boundary situated at a finite distance from the source, the
decline of the intensity can be described by the exponential
function with the standard value of the characteristic decay time
which does not depend on the parameters of the surrounding
plasma and the spectrum of particles.
( J is the flux of particles
and
r is the distance from the source), the time profile of fluxes
at the decay phase of the event has a power law shape and it is
proportional to
t-3/2, where
t is the time from the moment of the
injection of particles. In diffusion models with the absorbing
boundary situated at a finite distance from the source, the
decline of the intensity can be described by the exponential
function with the standard value of the characteristic decay time
which does not depend on the parameters of the surrounding
plasma and the spectrum of particles. 10 MeV, convective
transport and adiabatic cooling begin to play substantially
greater role and the decline of particle fluxes becomes
exponential
[Lee,
10 MeV, convective
transport and adiabatic cooling begin to play substantially
greater role and the decline of particle fluxes becomes
exponential
[Lee, 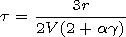
 2 for nonrelativistic particles. As far as we consider in
this paper measurements conducted on IMP 8, we shall not
touch the
τ dependence on the distance from the source,
assuming the Sun to be always such a source. It should be
mentioned that
Kecskeméty et al. [2005]
showed that on the
basis of the currently existing simultaneous measurements in
high energy channels on board Ulysses (3-5 AU) and IMP 8 (in
these measurements 49 events of the solar cosmic rays (SCR) on
Ulysses were identified reliably with the events at 1 AU) the rate
of proton fluxes decline both at low (4-5 MeV) and high
( >30 MeV) energies at 1 AU is always higher than at 3-5 AU.
However, for several events the time profiles for protons with
energies
>30 MeV on IMP 8 and on Ulysses coincided
[McKibben et al., 2001, 2003].
For the explanation of this
phenomenon, these authors used the proposed earlier model of
"the homogeneous reservoir of particles"
[McKibben, 1972;
Roelof et al., 1992].
This, however, does not change the general
picture.
2 for nonrelativistic particles. As far as we consider in
this paper measurements conducted on IMP 8, we shall not
touch the
τ dependence on the distance from the source,
assuming the Sun to be always such a source. It should be
mentioned that
Kecskeméty et al. [2005]
showed that on the
basis of the currently existing simultaneous measurements in
high energy channels on board Ulysses (3-5 AU) and IMP 8 (in
these measurements 49 events of the solar cosmic rays (SCR) on
Ulysses were identified reliably with the events at 1 AU) the rate
of proton fluxes decline both at low (4-5 MeV) and high
( >30 MeV) energies at 1 AU is always higher than at 3-5 AU.
However, for several events the time profiles for protons with
energies
>30 MeV on IMP 8 and on Ulysses coincided
[McKibben et al., 2001, 2003].
For the explanation of this
phenomenon, these authors used the proposed earlier model of
"the homogeneous reservoir of particles"
[McKibben, 1972;
Roelof et al., 1992].
This, however, does not change the general
picture.
