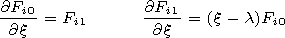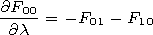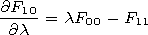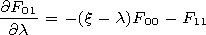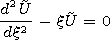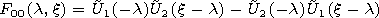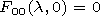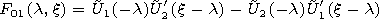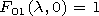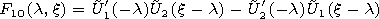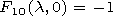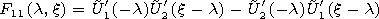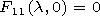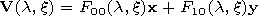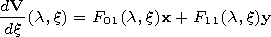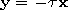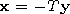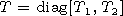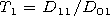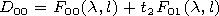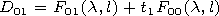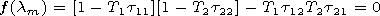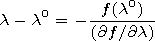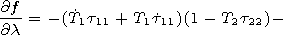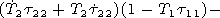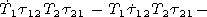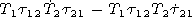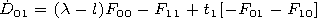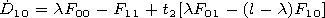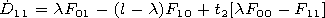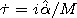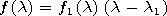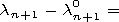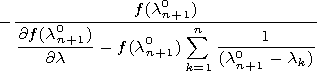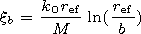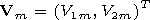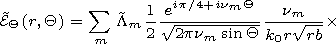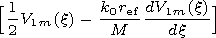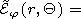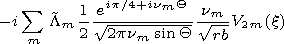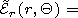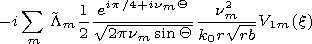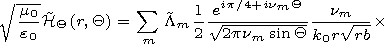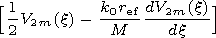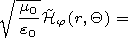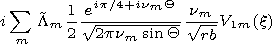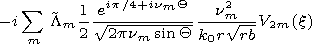4. Method of Calculation of Normal Wave
Characteristics for Waveguides of Comparison
[16] Over a homogeneous spherical surface
r > a there is a
medium described by the dielectric permittivity tensor
e(r).
ne is the collision frequency of electrons with
neutral particles,
Ne is the electron concentration,
BE is the Earth magnetic field vector,
Y is the relative gyrofrequency of electrons in
the constant magnetic field of the Earth,
w is the angular
frequency, and
wpl is the plasma frequency.
One has to solve the problem to the eigenvalues, i.e.,
equation (4).
[17] The initial system of equations consists of 6 scalar equations,
however not all of them being differential ones. Using two
equations one can express the vertical components of the vectors
Emr and
Hmr
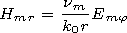 | (15) |
and obtain a new system of four differential equations
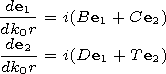 | (16) |
[18] It is known that a numerical integration of system (16) requires
special approaches, because one has to separate two solutions
satisfying the condition of a decrease at the infinity out of four
independent solutions available. At the proper specification of
the initial conditions at a height of
ru, (the choice of
which was described in section 2) and integration from the top
downward, we get rid of two undesirable solutions, however out of
two solutions left, one will very quickly increase at the
integration. To obtain a solution stable to the integration
errors, we use a bivector formed from two solutions
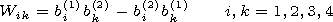 | (17) |
where
j is the number of the
solution of system (16)
j=1,2.
[19] The bivector is a skew-symmetric tensor
4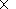 4. At its
diagonal there are zeros and
Wik=-Wki, so it has 6
independent elements. The bivector satisfies the following system
of equations:
4. At its
diagonal there are zeros and
Wik=-Wki, so it has 6
independent elements. The bivector satisfies the following system
of equations:
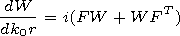 | (18) |
[20] We determine the initial values
Wik at a height
ru from the solution of the problem on the field of a plain wave in
the longitudinal approximation
Using the bivector elements, one
can obtain the matrix of the reflective properties of the
ionosphere
a which is determined by the relation
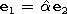 | (19) |
 | (20) |
The system of equations for the
a matrix is
nonlinear, so at its integration, singularities may arise
( W34 may reduce to zero). Such phenomena arise sometimes
for the equatorial ionosphere. Two points are merits of this new
method of bivector: the linearity of system (18) and the fact that
at no conditions the
Wik elements transform to the
infinity.
[21] At the
ru level, elements of the
a matrix do
not depend on the spectral parameter, so
Therefore it follows that the scalar
products
(Y+m, GYm),
determined at the intervals
[a,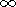 ) and
[a,ru], coincide.
) and
[a,ru], coincide.
[22] The characteristic equation for the eigenvalues of the waveguide
problem is obtained from the boundary conditions at the Earth
surface
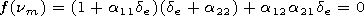 | (21) |
The
eigenvalues
nm are included into the coefficients of
equations (18); therefore the values of the matrix
a elements at the Earth surface depend on these values. To determine
nm, the Newton method
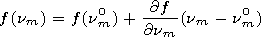 | (22) |
is used, where
nm0 is the initial approximation for the eigenvalue.
Then
[23] Numerical realization of this algorithm and the procedure
of the selection of initial approximations for eigenvalues are
discussed in the next paragraph.
[24] At the Earth surface, the derivatives of the
a matrix
elements with respect to the spectral parameter
 a/
a/  n are usually large, so presentation (22) is correct
at small
nm-nm0.
If the initial approximation is given
with insufficient accuracy, then to obtain the eigenvalue one
would need many iterations, and at each iteration system (18)
should be integrated together with the system for the derivatives
with respect to the spectral parameter
W=
n are usually large, so presentation (22) is correct
at small
nm-nm0.
If the initial approximation is given
with insufficient accuracy, then to obtain the eigenvalue one
would need many iterations, and at each iteration system (18)
should be integrated together with the system for the derivatives
with respect to the spectral parameter
W=  W/
W/ n
n
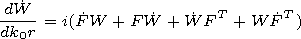 | (23) |
To rush the
iteration process, the following approach is used: functions
satisfying the boundary conditions at the Earth surface are
constructed in the vacuum spherical cavity, and the characteristic
equation is obtained from equation system (19) which is valid at
any height
r ef under the condition that at
r ef vacuum, i.e.
e1 and
e2 are
obtained for the vacuum. It is convenient to chose such height
r ef, where
a is least dependent on the
spectral parameter. We will call it an effective height. We chose
r ef according to the criterion
min 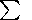 aik . Thus, calculating the
eigenvalues, systems (18) and (23) are integrated from
ru to
rl (see section 2). Then the same systems of
equations, but with the coefficients corresponding to the vacuum
eik=0 and
eii=1 are integrated
upward till the condition
min
aik . Thus, calculating the
eigenvalues, systems (18) and (23) are integrated from
ru to
rl (see section 2). Then the same systems of
equations, but with the coefficients corresponding to the vacuum
eik=0 and
eii=1 are integrated
upward till the condition
min 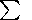 aik is fulfilled.
aik is fulfilled.
[25] For realization of the above described scheme of recalculation of
the
a matrix to the effective height
r ef, a
solution should be formed in the spherical cavity in the vacuum at
the given boundary conditions of an impedance type at the upper
and lower walls.
[26] Following Makarov et al. [1991]
and
Kirillov [1979],
we consider the electromagnetic field independent of the azimuthal
coordinate
j. We describe the field using the pair of the
Hertz potentials
U1 and
U2, satisfying in the cavity
a 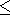 r
r 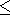 r ef to the following system of differential
equations:
r ef to the following system of differential
equations:
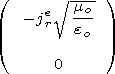 | (24) |
[27] The electromagnetic field is related to the potential by the
formulae
[28] The conditions of the impedance type for the potentials have the
following form:
at
r=a
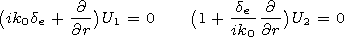 | (25) |
and at
r=r ef
 | (26) |
We solve the system
of differential equations (24) by the method of separation of
variables with expansion in terms of normal waves
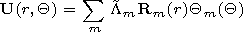 | (27) |
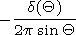 | (28) |
Substituting (27) into equation (24) and taking into account (28),
we obtain
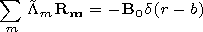 | (28') |
where
at the excitation of the field by a short antenna. The
d function in the right-hand sides of equations (28),
( 28' ) appears because the source of the field is a point dipole
situated at the height
b-a above the Earth's surface.
[29] The function
in the interval
is a limited solution of equation ( 28' ) at
Q=p. The function
Qm(Q) may be presented
in the form
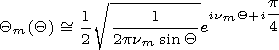 | (29) |
where we neglected the antipode wave and
around-the-globe waves. To obtain a solution bounded at
Q=0 the source, one should take into account the finite thickness of
the antenna. We present it as a hollow short truncated cone the
outer surface of which is described by
Q = e.
Further on we should construct a solution bounded in the region
Q e, to sew solutions in the regions
Q > e and
Q
e, to sew solutions in the regions
Q > e and
Q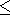 e at the boundary
Q = e in the way it is described in detail by
Makarov et al. [1991].
Since we are interested in the
distance much longer than the antenna thickness,
e may
be tended to zero, obtaining formula (29). We introduce new
functions
Vm, and
Rm= (r/b)1/2Vm(r) and new variable
e at the boundary
Q = e in the way it is described in detail by
Makarov et al. [1991].
Since we are interested in the
distance much longer than the antenna thickness,
e may
be tended to zero, obtaining formula (29). We introduce new
functions
Vm, and
Rm= (r/b)1/2Vm(r) and new variable
such that
Neglecting by the terms of the order of
(( r ef-a)/a)2 and
M/k0r ef we obtain the equation with the boundary
conditions
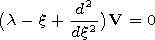 | (30) |
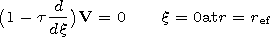 | (31) |
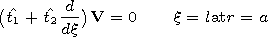 | (32) |
where
The vector function
V and spectral parameter
l are used at the formulation of the problem without
indices,
Vm is the eigenvector function, and
lm is the eigenvalue. The eigennumber
nm is
related to the new spectral parameter
lm by the
relation
nm=k0ref(1-lm/M2)1/2.
[30] Complex conjugate values of the eigenfunctions of the adjoint
operator
V+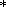 m satisfy equation (30) with the
same boundary conditions but only with the transposed matrix
t. We multiply equation (30) with the spectral parameter
lm and function
Vm to the function
V+
m satisfy equation (30) with the
same boundary conditions but only with the transposed matrix
t. We multiply equation (30) with the spectral parameter
lm and function
Vm to the function
V+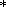 n, satisfying equation (30) with the spectral
parameter
ln. We multiply equation (30) to
Vm and subtract the latter from the former. Then
n, satisfying equation (30) with the spectral
parameter
ln. We multiply equation (30) to
Vm and subtract the latter from the former. Then
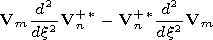 | (33) |
We integrate (33) with respect to
x within the
spherical cavity
(0,l) and obtain
 | (34) |
If the boundary condition for
Vm and
V+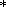 n at
x = l and
x = 0 does not depend
on the spectral parameter, then the right-hand side of (34) tends
to 0 and the functions
Vm and
V+
n at
x = l and
x = 0 does not depend
on the spectral parameter, then the right-hand side of (34) tends
to 0 and the functions
Vm and
V+ n form an orthogonal system.
n form an orthogonal system.
[31] To construct the eigenfunctions
Vm(x) we consider
two independent solutions of equation (30)
Fi0(l,x)
(i=0,1) and their
derivatives
Fi1(l,x). They in pairs satisfy
the following system
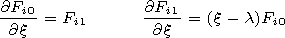 | (35) |
with the initial conditions
 | (36) |
Functions
Fi0(l,x) are the Airy's
functions and the Jacobian composed of two solutions
Fi0(l,x), is independent of
x
 | (37) |
As functions of the
l parameter,
Fik(l,x) satisfy the following system of
differential equations
 | (38) |
System (38) makes it possible to continue analytically
in terms of
l the aggregate of the functions
Fik(l,x), if they are known at some
l.
System (38) is obtained in the following way. Let
U1(x) and
U2(x) be 2 independent
solutions of the Airy's equation
Then the system of equations (35) is satisfied
if one takes
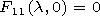 | (38') |
where
Thus, relations
(35), (36), and (37) are satisfied. We differentiate (38) with
respect to
l and obtain system ( 38' ).
The vector-function
V(l,x) and its derivative
[d V/ dx](l,x) are expressed via
Fik(l,x) in the following way
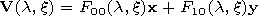 | (39) |
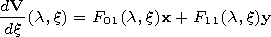 | (40) |
where vectors
x and
y are independent of
x. Using the initial values (36) at the upper wall of the
waveguide
(x=0), we obtain
The boundary
conditions are satisfied if
At the lower wall of the waveguide under
x=l, the
boundary conditions are satisfied if
where
 | (40') |
Here
t1=-iMd1 and
t2=id2/M.
To fulfill
the conditions at the lower and upper boundaries, the equality
should be valid
 | (41) |
Equation system (41) relative
x1 and
x2 is linear and homogeneous. For the existence of a nonzero
solution, the determinant should be made to vanish.
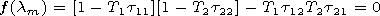 | (42) |
Equation (42) may be considered as characteristic
equation recalculated from the Earth surface to the effective
height, and its roots are the eigenvalues
lm. The
T and
t matrices are functions of
lm.
[32] The roots of equation (42) are looked for by the iteration method,
the convergence of the process depends on the accuracy of taking
the initial approximations
l0. The method of
calculation of the initial approximations was developed by
Kirillov [1979, 1981, 1983].
This method is based on the
utilization of eigenvalues corresponding to the waveguide with
ideally conducting lower boundary and magnetic upper boundary by
insertion of corrections that take into account finite values of
electric and magnetic parameters of the boundaries. The correction
to the spectral parameter
l is found in the following way
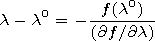 | (43) |
where
Here dot denotes a differentiation with respect to the
spectral parameter
l. The found eigenvalues are excluded
out of characteristic equation (42) while looking for the next
values. Let
l1 is found. Then the characteristic
equation may be presented in the form
and we obtain the corrections to the eigenvalue by the
formula
Let
n eigenvalues are found. Then
looking for the n+1 value, we use the formula
For
determination of the excitation coefficients or amplitudes of the
normal waves, we rewrite equation (28' ) in terms of the
introduced functions
Vm of the variable
x
 | (44) |
where
We multiply scalarly the left-hand side of equation (44)
to the eigenfunction of the adjoint operator
Vm+ and, taking them orthogonal at the interval
[0,l], we obtain the
excitation coefficient of the field by a short vertical antenna
 | (45) |
We write out the components of the electromagnetic field in the
vacuum cavity of a regular waveguide
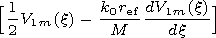 | (46) |
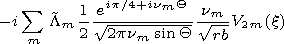 | (47) |
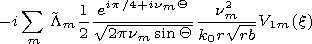 | (48) |
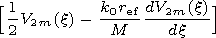 | (49) |
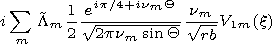 | (50) |
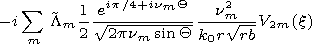 | (51) |

Powered by TeXWeb (Win32, v.2.0).
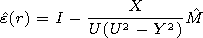
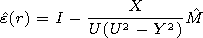
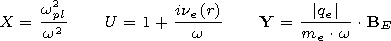
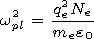
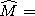
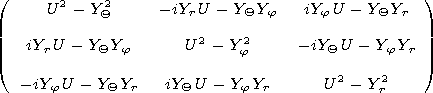
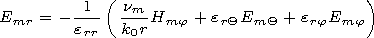
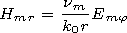
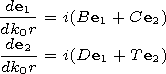

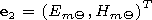
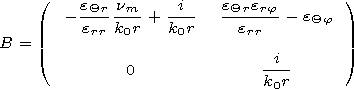

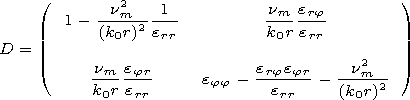

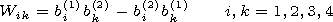
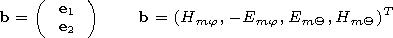

 4. At its
diagonal there are zeros and
Wik=-Wki, so it has 6
independent elements. The bivector satisfies the following system
of equations:
4. At its
diagonal there are zeros and
Wik=-Wki, so it has 6
independent elements. The bivector satisfies the following system
of equations: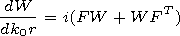
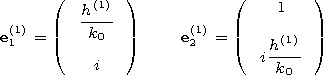
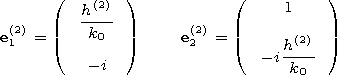
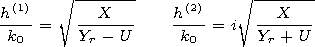
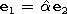
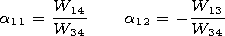


 ) and
[a,ru], coincide.
) and
[a,ru], coincide.
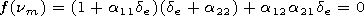
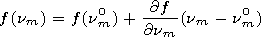
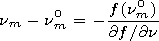
 a/
a/  n are usually large, so presentation (22) is correct
at small
nm-nm0.
If the initial approximation is given
with insufficient accuracy, then to obtain the eigenvalue one
would need many iterations, and at each iteration system (18)
should be integrated together with the system for the derivatives
with respect to the spectral parameter
W=
n are usually large, so presentation (22) is correct
at small
nm-nm0.
If the initial approximation is given
with insufficient accuracy, then to obtain the eigenvalue one
would need many iterations, and at each iteration system (18)
should be integrated together with the system for the derivatives
with respect to the spectral parameter
W=  W/
W/ n
n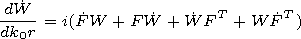
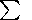 aik . Thus, calculating the
eigenvalues, systems (18) and (23) are integrated from
ru to
rl (see section 2). Then the same systems of
equations, but with the coefficients corresponding to the vacuum
eik=0 and
eii=1 are integrated
upward till the condition
min
aik . Thus, calculating the
eigenvalues, systems (18) and (23) are integrated from
ru to
rl (see section 2). Then the same systems of
equations, but with the coefficients corresponding to the vacuum
eik=0 and
eii=1 are integrated
upward till the condition
min 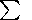 aik is fulfilled.
aik is fulfilled.
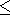 r
r 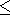 r ef to the following system of differential
equations:
r ef to the following system of differential
equations:
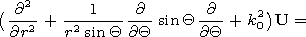
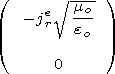

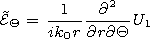
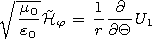
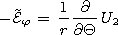
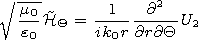
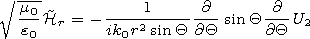
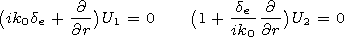

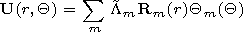
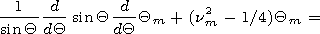
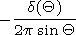

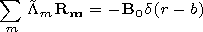
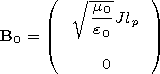

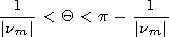
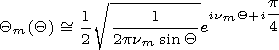
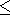 e, to sew solutions in the regions
Q > e and
Q
e, to sew solutions in the regions
Q > e and
Q e at the boundary
Q = e in the way it is described in detail by
Makarov et al. [1991].
Since we are interested in the
distance much longer than the antenna thickness,
e may
be tended to zero, obtaining formula (29). We introduce new
functions
Vm, and
Rm= (r/b)1/2Vm(r) and new variable
e at the boundary
Q = e in the way it is described in detail by
Makarov et al. [1991].
Since we are interested in the
distance much longer than the antenna thickness,
e may
be tended to zero, obtaining formula (29). We introduce new
functions
Vm, and
Rm= (r/b)1/2Vm(r) and new variable
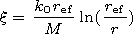

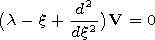
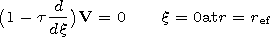
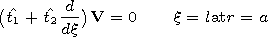


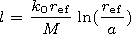
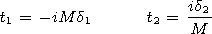
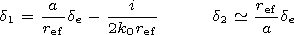
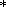 m satisfy equation (30) with the
same boundary conditions but only with the transposed matrix
t. We multiply equation (30) with the spectral parameter
lm and function
Vm to the function
V+
m satisfy equation (30) with the
same boundary conditions but only with the transposed matrix
t. We multiply equation (30) with the spectral parameter
lm and function
Vm to the function
V+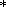 n, satisfying equation (30) with the spectral
parameter
ln. We multiply equation (30) to
Vm and subtract the latter from the former. Then
n, satisfying equation (30) with the spectral
parameter
ln. We multiply equation (30) to
Vm and subtract the latter from the former. Then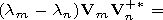
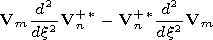
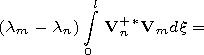


 n at
x = l and
x = 0 does not depend
on the spectral parameter, then the right-hand side of (34) tends
to 0 and the functions
Vm and
V+
n at
x = l and
x = 0 does not depend
on the spectral parameter, then the right-hand side of (34) tends
to 0 and the functions
Vm and
V+ n form an orthogonal system.
n form an orthogonal system.