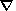Application of the normal wave method to calculations of VLF...

2. Description of the Waveguide Channel Model

[4] The Earth surface is modeled by a sphere of the radius a, at which the impedance conditions are taken. In this case we exclude out of the regime the waves propagating mainly under the Earth surface because they are insignificant at distances R exceeding the thickness of the skin layer in the Earth. For determination of the impedance in any observational point, a model of the Earth homogeneous by the depth described by Morgan [Morris and Lha, 1974] is used.

[5] Over the Earth surface, we have an ionized medium located within a constant magnetic field. The Earth magnetic field is presented in the form B_E=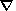 nabla u, where the potential u is approximated by the expression

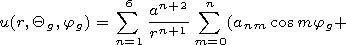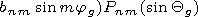where Q_g and j_g are the geographic latitude and longitude, respectively, a is the Earth radius, P_n0( sinQ_g) = P_n( sinQ_g) is the Legendre polynomial, and P_nm( sinQ_g) is the associated Legendre function. The coefficients a_nm and b_nm different from zero are presented below expressed in nT:

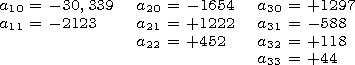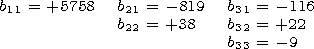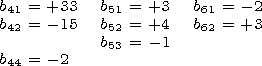The concentration and collision frequency of electrons are functions of the height over the Earth surface and are taken according to any known model.

[6] In undisturbed conditions, the plasma frequency w_pl at altitudes up to 50 km over the Earth surface is considerably less than the electron collision frequency with neutral particles, so in the near-Earth region the relative dielectric permittivity of the medium e does not differ from its value in the vacuum. So in the used model the lower boundary of the ionosphere is determined as the level where e(r_l)-1r_u, above which the characteristic scale of changes in the medium properties l (l= max | (1/e_ik) ( partial e_ik/ partial r) |^-1, where e_ik is the tensor of relative dielectric permittivity of the ionosphere) is much larger than the characteristic scale of the field changes in r, so calculating this scale 1/h one may take the medium as homogeneous (Booker roots) [Budden, 1961a]

k₀ is the wave number in the vacuum, k₀ = w(e₀m₀)^1/2, e₀ is the dielectric permittivity of the vacuum, m₀ is the magnetic permittivity of the vacuum, q_e is the electron charge value, w is the circular frequency of the electromagnetic field, m_e is the electron mass, B_E is the magnetic induction of the Earth field, and at r geq

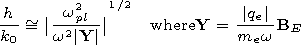r_u the inequality h/ k₀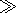

1 should be fulfilled. Then above r_u the field structure may be taken as a plain wave propagating vertically independently of the field structure at r< r_u and independently of the source of excitation of the electromagnetic field.

[7] We chose the level r_u in such a way that h/ k₀=p2 were large enough. Actually, the accuracy of calculation of eigenvalues of the normal waves is determined by the choice of r_l and r_u (the boundaries of the ionospheric layer called the region important for propagation). In particular, the choice of the p1=10^-4 and p2=30 parameters provides the relative error of calculation of the eigennumber not more than 10^-4.

[8] The problem of calculation of the fields within the waveguide channel Earth-ionosphere excited by the antenna located at some height over the Earth surface is formulated. The antenna orientation is given by the angle Q_p relative to the vertical axis and by the azimuthal angle j_p, counted clockwise from the direction to the receiver. Jl_p is the current moment of the transmitting antenna. In the observational point, the field is received by the antenna located at any level relative to the Earth surface. The orientation of the receiving antenna is given by the angle Q_a relative the vertical and by the azimuth angle j_a, counted clockwise from the transmitter-receiver direction. The induced electromotive force at the short receiving antenna is calculated by the formula

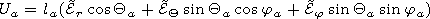where l_a is the virtual height of the short receiving antenna, and E_r, E_Q, and E_j are the corresponding components of the electric field intensity in the place of the receiving antenna location.

[9] Mathematically we formulate the problem for a vertical dipole and after its solution we will form the field for an arbitrary oriented short antenna applying the generalized reciprocity theorem.