Oblique chirp sounding and modeling of ionospheric HF...

2. Equipment and the Method of Data Processing

Figure 1

[13] The measurements were conducted at the radio paths of LFM sounding of different length and orientation: Cyprus (35^oN, 34^oE)—Rostov-on-Don (47.2^oN, 39.7^oE) (the path length is 1440 km, the geographical azimuth from Rostov-on-Don is 203.2^o), Inskip (England, 53.8^oN, 2.8^oW)—Rostov-on-Don (3043 km, 300^o), Norilsk (69.4^oN, 88.2^oE)—Rostov-on-Don (3587 km, 29.8^o), Irkutsk (52.3^oN, 104.2^oE)—Rostov-on-Don (4512 km, 57.8^o), Magadan (59.6^oN, 150.8^oE)—Rostov-on-Don (6615 km, 33.4^o). At two former paths the measurements were carried out during the entire 2005 around the clock with one ionogram recorded every 5 min. At the latter three paths the measurements were carried out during September 2005 around the clock with the interval of one ionogram recording of 15 min at each path. The reception point was located at Rostov-on-Don. Geometry of paths is shown in Figure 1.

[14] Two-channel chirp sounder created on the basis of the "Katran'' R-399 A receiver was used in the measurements. The rate of the frequency sweeping was 100 kHz s ^-1. The range of emitting frequencies was 8-30, 4.2-30, and 4-30 MHz for Cyprus, Inskip, and the rest of the transmitters, respectively. Two 9-m collapsible-whip antennas were used for the reception. The time synchronization of the start of reception of LFM signals was provided with the help of GPS with the error less than 10 ms. The residual signal was digitized at intermediate frequency (IF) ( f = 215 kHz) using the 14-digit analog-digital transformer (ADT) with the frequency discreteness of 50000 Hz, the latter value exceeding considerably the used transmission band of the receiver at IF (3000 Hz).

[15] The signal transformation and its processing included the following stages. The received residual signal was put through the procedures of a transfer to the zero frequency with obtaining quadrature components (complex low-frequency envelope), low-frequency filtration by a digital filter with the transmission band of 500 Hz, and decimation with the reduction of the discreteness frequency down to 3000 Hz. As a result, the procedure described increased the dynamical range not less than by 10 dB. The procedures of digitalization, filtration, signal quadrature revealing, and decimation were organized in such a way that the entire preliminary processing was performed in real time in an automatic way and made it possible to obtain continuous recordings of unlimited duration in time. Further spectral processing of the differential signal was performed based on multitaper method [Thomson, 1982] with the aim to extract continuous and discrete components of spectral density of power. The determination of ray parameters (the amount of rays, their amplitudes and time delays) is based on the estimation of the discrete components in the spectrum of the residual signal. Such estimate is checked up based on the threshold statistical criterion (statistics of F distribution) [Thomson, 1982]. Noise spectral density and the ratio of the signal power to the noise power in the reception band consistent with the signal are determined by the histogram method assuming that the frequency band of the spectral analysis is much larger than the frequency band of the receiving signal. For such purpose the histogram of the power spectral density is obtained in the frequency band of the receiver. The maximal level of histogram corresponds to the probable value of the noise spectral density during the period of the data obtaining. After that the ratio of the signal power to the noise power is determined quite evidently. As a result of the processing in real time, the following parameters were determined: the level of the noise spectral density in the reception band, the number of detected propagation rays, amplitudes of all rays, the signal-to-noise ratio for each ray, and absolute delays of each of detected rays [Vertogradov, 2005].

[16] Further processing had the aim to obtain the frequency-time and frequency-amplitude display ionograms. Frequency-delay and frequency-amplitude display of the single propagating rays and modes are formed by comparison of the obtained parameters in the multivariate space frequency-time-amplitude. Each point that at the beginning was identified with some ray is characterized by three coordinates: f_j - frequency, t_jl - time delay, a_jl - amplitude of the l th ray on the j th frequency. The amount of rays, n_j, and their coordinates in the three-dimensional (3-D) space are determined according to the algorithm described above in the process of spectral processing based on multiple-taper method spectral analysis. In the 3-D space frequency-time-amplitude we introduce the distance between points according to the rule

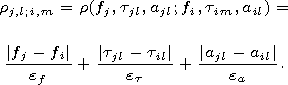[17] Two points that correspond to the neighbor frequencies f_j-1 and f_j with the indices l and m are assumed to belong to the same frequency branch if the relation r_j,l;j-1,m < 3 is realized. The parameters e_f, e_t, and e_a are selected empirically and assumed to be 500 kHz, 0.1 ms, and 3 dB correspondingly. If for some point the correspondence with the previous points is not established, then we assume that this point relates to a new branch. As a consequence at the end of the process of sounding many frequency branches are formed. After that the procedure of the secondary processing takes place. At this stage the regions restricted by the lowest (LOF) and the maximal (MOF) observed frequencies are found for each branch. The total amount of these regions for all frequency branches provides the opportunity to determine the intervals: the frequency intervals where one ray, two rays, three rays, etc., exist. From the MOF for all rays the MOF of the path is determined as the maximal frequency from all observed frequencies. From the lowest frequencies the LOF of the path is determined as the minimal frequency from all observed frequencies.

Figure 2

[18] The band of the analysis of the residual signal was 65 kHz, the latter value providing the separation of modes and propagation rays with a resolution better than 15 m s. The spectral processing of the residual signal was performed with the time window equal to 650 ms. At each step it was shifted at 1/16 part. So the points in the space frequency-time-amplitude are separated by ~4 kHz. As a consequence, the accuracy with which the frequency boundaries of multiray region and the tool accuracy of the LOF and the MOF estimate comprises ~4 kHz. As the signal is the diffuse one, the real accuracy of the LOF and the MOF estimate comprises ~10-20 kHz. Examples of frequency-time and frequency-amplitude display for the Cyprus—Rostov-on-Don path (where the effects of wave disturbances

Figure 3

are manifested in the most visual way) are shown in Figures 2 and 3. Figure 2 shows the dynamics of transportation of a wave disturbance (z-type features) at the track of the high-angle ray for 1F mode. Figure 3a shows an example of registration of several high-angle rays accompanied by the F spread phenomenon. Figure 3b illustrates the effect of quasi-regular amplitude-frequency modulation of the high-angle ray. The effect is well seen at frequency time display for the track of extraordinary mode of high-angle ray (Figure 3b, top), and also at frequency-amplitude display (Figure 3b, bottom) for the ordinary and extraordinary modes of high-angle ray (Pedersen mode), marked as 1F_po and 1F_px, respectively. Figures 3c and 3d show examples of registration of ionospheric disturbances simultaneously at modes 1F and 2F. In the procedure of processing, the amplitude display were reduced to the maximum digitalization of the amplitude-digital transformer (ADT), in other words, 0 dB corresponds to digitalization of the sinusoidal signal with the amplitude equal to the maximum digits of ADT. It is worth noting also that the amplitude of separated rays was determined by integrating of the spectral density of the residual signal over the vicinity of the maximums in the spectrum limited by the nearest maximums from the right-hand and left-hand sides. This operation made it possible to reach much higher accuracy of measuring the amplitudes of partial rays than just use of the amplitude value in the maximum of the spectral density.

[19] The further processing of frequency-time and frequency-amplitude display ionograms at the studied paths was aimed at (1) obtaining of the diurnal variations of the maximum observed frequency of particular propagation modes, MOF was determined for extraordinary modes; (2) obtaining of averaged monthly mean variations in MOF of particular propagation modes; (3) comparison of the averaged monthly mean values of MOF with the forecasted values based on the International Reference Ionosphere IRI 2001; (4) spectral analysis of the time variations in MOF; (5) analysis of the frequency-time display and its variations caused by TID; and (6) analysis of the frequency-time display for particular propagation modes and comparison of the experimental dependencies with the results of modeling.