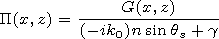3. Determination of the Hertz Potential
|
|
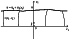
Figure 2
|
[6] To solve the above formulated problem, we use the conformal
mapping
x(u) transforming the
z  h
region of the
complex plane
u = x + i z into some one cohesive region
z1
h
region of the
complex plane
u = x + i z into some one cohesive region
z1  f(x1) of the
x = x1 + i z1 plane (see Figure 2).
Under such transformation, the
z = h plane is transformed into a
curved surface
z1 = f(x1), and the boundary problem (2)-(3)
is rewritten in the
(x1, z1) coordinate system in the form
f(x1) of the
x = x1 + i z1 plane (see Figure 2).
Under such transformation, the
z = h plane is transformed into a
curved surface
z1 = f(x1), and the boundary problem (2)-(3)
is rewritten in the
(x1, z1) coordinate system in the form
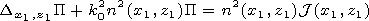 | (4) |
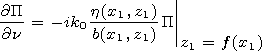 | (5) |
Here
 /
/ n is the derivative along the normal
to the line of the curved boundary, and the values
and
are, respectively, modulus of the derivative of the mapping
x(u) and of the inverse to it transformation
u(x) (it is
evident that
b = 1/n ).
n is the derivative along the normal
to the line of the curved boundary, and the values
and
are, respectively, modulus of the derivative of the mapping
x(u) and of the inverse to it transformation
u(x) (it is
evident that
b = 1/n ).
[7] Using the uncertainty in the
b(x1, z1) function, we choose it
in such a way that the equality
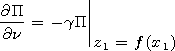 | (6) |
(where
g = i k0 h0 = const ) would be
fulfilled. Therefore, at the boundary
Finally we come to the problem on electromagnetic wave propagation
in the semispace with the known inhomogeneous refraction index and
one-dimensionally curved boundary having a constant impedance.
[8] To solve the boundary problem (4), (6), we apply the operator
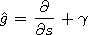 | (7) |
to the right-hand and left-hand sides of the equation (4).
Here
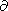 /
/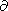 s is the derivative along the direction
of the tangent line to the
s(x1,z1) curve (see Figure 2). We
put on the family of curves
s the following requirements:
s is the derivative along the direction
of the tangent line to the
s(x1,z1) curve (see Figure 2). We
put on the family of curves
s the following requirements:
[9] 1. Only one line
s passes through every point of the
(x1,z1) plane.
[10] 2. In the point of the boundary
z1 = f(x1) the direction of the tangent line to the corresponding curve of the
s family coincides with the direction of the normal
n along which the differentiation in the boundary condition (6)
is performed (see Figure 2 where the
s(x1,z1) curves are shown
by dashed curves).
Therefore at the points of the curved boundary, the following equality
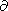 /
/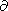 s =
s = 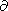 /
/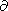 n is true.
n is true.
[11] For the sake of certainty, we choose particular family
s as a set of
curves that are transformed into the lines
x = const under the inverse conformal mapping
u(x),
which transforms the considered curved
semispace
z1 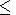 f(x1) of the complex plane
x = x1 + i z1 into the
z
f(x1) of the complex plane
x = x1 + i z1 into the
z 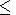 h region
of the
u = x + i z plane. Under this transformation, the curve
z1 = f(x1) is transformed into the line
z = h.
h region
of the
u = x + i z plane. Under this transformation, the curve
z1 = f(x1) is transformed into the line
z = h.
[12] In an analogy with Zaboronkova et al. [2003]
we perform conformal transformation in variables
(x1, z1) and
then come back to the initial coordinates
(x,z). Zaboronkova et al. [2003]
demonstrated that for the function
satisfying the Dirichlet's zero condition at the upper boundary,
it is true
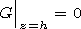 | (8) |
Therefore we come to the following equation in the initial
variables
(x,z):
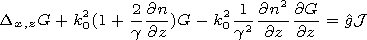 | (9) |
In the same way as Al'pert et al. [1953] and Bezrodny et al. [1984], we will consider the case of a
grazing propagation when the horizontal distance
x from the source to the observational point is much larger than the
vertical distance
h from this point to the disturbed boundary.
In this case the
grazing
angle of the falling wave is
qs 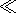 1. In such case, with the accuracy of the terms
1. In such case, with the accuracy of the terms
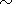 qs2, the following relation is true:
Then we are able to rewrite the equation (9)
in the form
qs2, the following relation is true:
Then we are able to rewrite the equation (9)
in the form
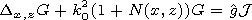 | (10) |
where
Here and further the function
1+N(x, z) is interpreted as the
dielectric permeability of the effective "medium". Such "medium"
is interpreted as an internal factor connected with the method of
solution of the problem. To each type of the impedance,
inhomogeneity corresponds its own dependence
N(x, z). To solve
the auxiliary boundary problem (8) and (10), we apply the
geometric optic method (because
l/lg 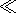 1 ). Using
the methodology of Al'pert et al. [1953], we assume
that in the
z
1 ). Using
the methodology of Al'pert et al. [1953], we assume
that in the
z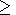 h region there exists an effective medium with
the dielectric permeability
e+ = 1 + N(x,z - h) symmetric relative to the permeability
e- = 1 + N(x,z) of the medium at
z
h region there exists an effective medium with
the dielectric permeability
e+ = 1 + N(x,z - h) symmetric relative to the permeability
e- = 1 + N(x,z) of the medium at
z 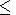 h. We designate the
corresponding refraction indices as
n
h. We designate the
corresponding refraction indices as
n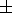 = (e<img src="latex006.gif" alt="pm">)1/2. We assume that in the point
M0'(0, 2h) symmetrical to
M0(0,0) (the place of the location of the source (1)
relative to
the plane
z = h, there is an imaginary source
j', the
auxiliary function
G=[n (
= (e<img src="latex006.gif" alt="pm">)1/2. We assume that in the point
M0'(0, 2h) symmetrical to
M0(0,0) (the place of the location of the source (1)
relative to
the plane
z = h, there is an imaginary source
j', the
auxiliary function
G=[n (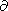 /
/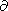 (- z)) + g ]P corresponding to this source [see Al'pert et al., 1953]. It is evident that at the
z = h level the
sum of the fields of these two sources is equal to zero. So the
boundary condition (8) is automatically satisfied.
(- z)) + g ]P corresponding to this source [see Al'pert et al., 1953]. It is evident that at the
z = h level the
sum of the fields of these two sources is equal to zero. So the
boundary condition (8) is automatically satisfied.
[13] We designate as
G1 fal and
G1 ref the auxiliary function
for the wave from the source
(1)
falling from below onto the boundary
z =h and for the
corresponding reflected wave, respectively. Then
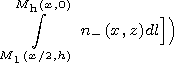 | (11) |
Here
M1 = M1(x/2,h) is the central point of the region
important for reflection from the weak boundary
z = h [see Ginzburg, 1960],
R1 = R1 (x/2,h), and
Rh = Rh (x,0).
The value
A is the amplitude of the function
G1 fal,
multiplier
r and multiplicand
T are the refraction and transmission indices,
respectively, and the factor
A determines the
divergence of the ray reflected from the boundary [see Kravtsov and Orlov, 1980].
[14] In a similar way we introduce an auxiliary function
G2 tr for the waves arriving from above from the source
j':
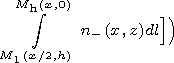 | (12) |
Here
R0' = R0'(0, 2h) is the radius vector of
the point
M0' determining the coordinates of the symmetrical
source
j'. We can also write
A( Rh - R0' ) =A( R1 - R0' ) A( Rh - R1). It follows from the problem symmetry that
(that is why, in particular, the phases of the functions
G1 ref and
G2 tr coincide) and
A( R1 - R0' ) = A( R1 - R0).
[15] Finally, we have
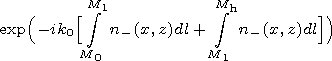 | (13) |
Here it is taken into account that
1 + r = T. Thus the
formulated problem is reduced to a calculation of the amplitude
and phase of the ray propagating in a smoothly inhomogeneous
medium with the dielectric permeability
e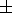 .
.
[16] Taking into account grazing propagation, one can easily obtain
from the expression
G= gP an approximate formula for
calculation of the
Hertz potential
P with the accuracy to the terms of the order of
qs2:
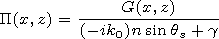 | (14) |
[17] On the basis of the derived formulae (13) and (14), we will
study the influence of different kinds of IGW on propagation of
electromagnetic waves. Let us consider two cases that correspond
to the models with imaginary and real impedance values at the
upper reflecting boundary. In particular, we will consider the
impact of the IGW of periodical and soliton types.

Powered by TeXWeb (Win32, v.2.0).


 h
region of the
complex plane
u = x + i z into some one cohesive region
z1
h
region of the
complex plane
u = x + i z into some one cohesive region
z1  f(x1) of the
x = x1 + i z1 plane (see Figure 2).
Under such transformation, the
z = h plane is transformed into a
curved surface
z1 = f(x1), and the boundary problem (2)-(3)
is rewritten in the
(x1, z1) coordinate system in the form
f(x1) of the
x = x1 + i z1 plane (see Figure 2).
Under such transformation, the
z = h plane is transformed into a
curved surface
z1 = f(x1), and the boundary problem (2)-(3)
is rewritten in the
(x1, z1) coordinate system in the form
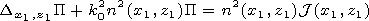
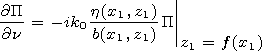
 /
/ n is the derivative along the normal
to the line of the curved boundary, and the values
n is the derivative along the normal
to the line of the curved boundary, and the values
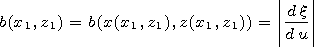
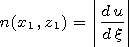
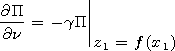
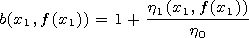
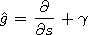
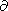 /
/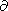 s is the derivative along the direction
of the tangent line to the
s(x1,z1) curve (see Figure 2). We
put on the family of curves
s the following requirements:
s is the derivative along the direction
of the tangent line to the
s(x1,z1) curve (see Figure 2). We
put on the family of curves
s the following requirements:
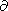 /
/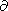 s =
s = 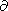 /
/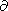 n is true.
n is true.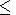 f(x1) of the complex plane
x = x1 + i z1 into the
z
f(x1) of the complex plane
x = x1 + i z1 into the
z 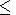 h region
of the
u = x + i z plane. Under this transformation, the curve
z1 = f(x1) is transformed into the line
z = h.
h region
of the
u = x + i z plane. Under this transformation, the curve
z1 = f(x1) is transformed into the line
z = h.
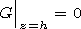
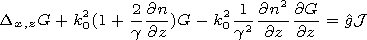
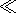 1. In such case, with the accuracy of the terms
1. In such case, with the accuracy of the terms
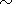 qs2, the following relation is true:
qs2, the following relation is true:
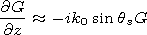
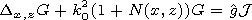
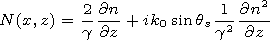
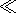 1 ). Using
the methodology of Al'pert et al. [1953], we assume
that in the
z
1 ). Using
the methodology of Al'pert et al. [1953], we assume
that in the
z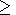 h region there exists an effective medium with
the dielectric permeability
e+ = 1 + N(x,z - h) symmetric relative to the permeability
e- = 1 + N(x,z) of the medium at
z
h region there exists an effective medium with
the dielectric permeability
e+ = 1 + N(x,z - h) symmetric relative to the permeability
e- = 1 + N(x,z) of the medium at
z 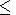 h. We designate the
corresponding refraction indices as
n
h. We designate the
corresponding refraction indices as
n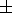 = (e<img src="latex006.gif" alt="pm">)1/2. We assume that in the point
M0'(0, 2h) symmetrical to
M0(0,0) (the place of the location of the source (1)
relative to
the plane
z = h, there is an imaginary source
j', the
auxiliary function
G=[n (
= (e<img src="latex006.gif" alt="pm">)1/2. We assume that in the point
M0'(0, 2h) symmetrical to
M0(0,0) (the place of the location of the source (1)
relative to
the plane
z = h, there is an imaginary source
j', the
auxiliary function
G=[n (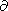 /
/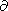 (- z)) + g ]P corresponding to this source [see Al'pert et al., 1953]. It is evident that at the
z = h level the
sum of the fields of these two sources is equal to zero. So the
boundary condition (8) is automatically satisfied.
(- z)) + g ]P corresponding to this source [see Al'pert et al., 1953]. It is evident that at the
z = h level the
sum of the fields of these two sources is equal to zero. So the
boundary condition (8) is automatically satisfied.
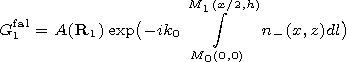
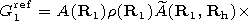

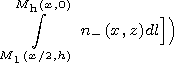
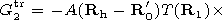
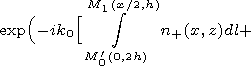
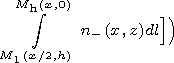
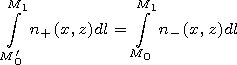
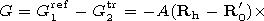
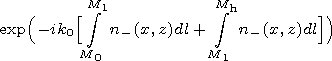
 .
.