3. Results
3.1. Internal Heating
[20] For the cases of internal heating, we varied
Pm and
assumed
h=0.6,
Ri=3000,
Re=-6000,
t=10,
P=1, and
m0=5. As can be seen from checking
computations with
m0=1 (not presented here), removing the
artificially imposed fivefold azimuthal symmetry does not
substantially modify the character of the convection pattern. The
quadratic term was present in the temperature dependence of
density, with a control parameter of
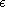 =0.005.
=0.005.

|
|
Figure 2
|
[21] The distributions of the temperature
TS(r) and its
gradient
d TS/d r for the corresponding
static-equilibrium state are shown in Figure 2. Obviously, the
outer part of the shell is convectively unstable and the inner
part is stable.

|
|
Figure 3
|
3.1.1. Case of Pm =30.
[22] At this
Pm value, the computations covered a time
interval of about 100 in units of the time of thermal diffusion
across the shell. Over most part of this period, a very stable
pattern of convection cells with a dodecahedral symmetry can be
observed (Figure 3, top). These cells have a normal appearance
typical of cellular convection, without substantial distortions
due to the rotation of the shell. The entire pattern drifts in the
retrograde direction, in agreement with theoretical predictions
[Busse, 2004].

|
|
Figure 4
|
[23] The axisymmetric component of the azimuthal velocity (Figure 4) in
a well-established flow pattern is nearly symmetric with respect
to the equatorial plane. Specifically, a prograde rotation of the
equatorial zone (in the frame of reference rotating together with
the entire body) is present along with a retrograde rotation of
the midlatitudes, and pairs of "secondary" prograde- and
retrograde-rotation zones can also be noted in the polar regions.
In a nonrotating frame of reference, the equatorial zone rotates
more rapidly and the midlatitudinal zones more slowly than the
shell as a whole does. Three pairs of meridional-circulation
vortices fill the entire meridional section of the shell, from one
pole to another.
[24] The pattern of magnetic field is less regular than the pattern of
flow (Figure 3, middle and bottom). Some remarkable features or
the simulated dynamo process can be summarized as follows.
[25] First, local magnetic structures associated with convection cells
emerge repeatedly as compact magnetic regions (see Figure 3). In
their subsequent evolution, these regions change their
configuration and finally dissipate into much weaker remnant
fields.
|
|
Figure 5
|
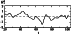
[26] Second, the dipolar component of the global magnetic field
exhibits polarity reversals (see Figure 5 for a graph of the
amplitude of the dipole component,
H10(t); wherever the
r variable as an argument of
H10 is omitted, we mean
H10(ri+0.5,t) ). The background fields, remnants of the
decaying local magnetic structures, drift toward the poles and
"expel" the "old" background fields present in the polar
regions. As a result, the old magnetic polarity is replaced with
the new one due to the poleward drift of the latter. The polarity
reversals of the global magnetic field can also be seen from the
variation in the amplitude of the dipolar harmonic of the poloidal
field,
H10(t) (Figure 5). The two maps of the magnetic field
shown in Figure 3 correspond to two situations in which the global
magnetic dipole has opposite orientations (the polarity reversal
between these two times corresponds to the rightmost intersection
of the curve in Figure 5 with the horizontal zero line).
|
|
Figure 6
|
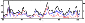
[27] Third, an interesting intermittent behavior is exhibited by the
magnetic energy of the system. Let us compare the full energy and
two particular fractions of the energy associated with the
magnetic field component that has a dipolar-type symmetry (i.e.,
is antisymmetric with respect to the equatorial plane).
Specifically, we are interested in the behavior of the energy of
the axisymmetric and the nonaxisymmetric part of this component.
The axisymmetric part is represented by the spherical harmonics
with
l odd and
m=0 (see (12)), and the nonaxisymmetric part by
other harmonics with
l+m odd. As can be seen from Figure 6 (in
which the total energy and its particular fractions are divided by
the volume of the shell), the main peaks in the graph of the total
energy are alternately associated with increases in the energies
of the axisymmetric and the nonaxisymmetric part of the component
with a dipolar symmetry. In particular, the peak located near
t=42 is fed by the symmetric field; near
t=55, by the
asymmetric field; near
t=68, by both but with some predominance
of the symmetric part; and near
t=78, again by the asymmetric
part.
3.1.2. Same case of Pm=30 but with special initial conditions.
[28] In our attempts to find conditions for the realization of magnetic
field dynamics similar to the generally imagined pattern of a
hypothetical dynamo process with differential rotation as its
essential part (known since the qualitative model suggested by
Babcock [1961]
and
Leighton [1964, 1969]),
we made
an additional computational run. We specified all parameters to be
the same as in the case described above. However, the initial
conditions were chosen in such a way that, initially, the system
would more likely find itself within the attraction basin of the
expected dynamo regime in state space. To this end, we superposed
the nonaxisymmetric components of the velocity field and magnetic
field obtained in the above described run onto a pattern of
differential rotation with the equatorial belt accelerated
compared to higher latitudes and with an appropriate distribution
of the axisymmetric azimuthal magnetic field that has different
signs on the two sides of the equator.
[29] The computations have demonstrated that the system nevertheless
approaches virtually the same regime that was observed without
using such special initial conditions. Thus a closer similarity
between the numerical solution and the properties of the
hypothetical dynamos of the Babcock-Leighton type does not seem to
be achievable in the framework of this very simple model.
|
|
Figure 7
|
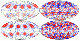
3.1.3. Case of Pm=200.
[30] As the magnetic Prandtl number
Pm is varied (under
otherwise fixed conditions), the convection pattern varies little
over a fairly wide
Pm range. However, the greater this
parameter, the higher the mean strength of the magnetic field
(and, accordingly, the total magnetic energy). The kinetic energy
of convection decreases with the increase of
Pm and
convection becomes more sensitive to time variations in the
magnetic field. The increase of
Pm is also manifest in
the fact that local magnetic fields become more patchy and less
ordered. Individual areas filled with the magnetic field of a
given sign are smaller in size and more numerous, and bipolar
structures are not so well pronounced (see Figure 7, which refers
to
Pm=200 ). As in the case of
Pm=30, we can
observe the penetration of background fields into the polar
regions and sign reversals of the polar background fields.

|
|
Figure 8
|
[31] Our computations for
Pm=200 cover a time interval almost
five times as long as for
Pm=30 (Figure 8). The two
velocity maps and two magnetic field maps shown in Figure 7 nearly
correspond to the times of one negative and one positive extremum
of the amplitude
H10(t) (see Figure 8). It is remarkable that
the polar background fields have different polarities at these two
times. At
t=200.0, the background magnetic field is negative in
the "northern" and positive in the "southern" polar region; an
opposite situation takes place at
t=327.2. The
H10(t) curve
demonstrates numerous sign reversals, although fine details of
this dependence only reflect the irregular, fluctuational aspect
of the process. It is nevertheless clear that, even if we smooth
this curve, it will exhibit quite pronounced cyclic, although
nonperiodic, polarity reversals of the dipolar component of the
"general" magnetic field.
[32] It should be noted that the distribution of the axisymmetric
component of the azimuthal velocity (the pattern of differential
rotation, not shown here) in this case is much more complex and
variable than at
Pm=30. This effect also can be due to
the stronger influence of the magnetic field on the fluid motion.
3.1.4. Internal heating without a
Q2
term (nonmagnetic case).
[33] To form an idea of the role played by the quadratic term in the
r(T) dependence, we computed a purely hydrodynamic (with
B=0 ) scenario under conditions that differed from the
conditions of the above described simulation by the absence of the
Q2 term ( 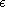 =0 ) and by the Coriolis number
( t=1 ); in addition, we assumed
m0=1 in this case.
=0 ) and by the Coriolis number
( t=1 ); in addition, we assumed
m0=1 in this case.

|
|
Figure 9
|
[34] The principal result of these computations is the finding that, in
the absence of the quadratic term, convection unaffected by the
magnetic field forms patterns of well-localized, three-dimensional
cells, which typically appear as shown in Figure 9. A downwelling
is observed in the center of each cell, in contrast to the above
described cases, in which central upwellings typically developed.
The issue of the direction of circulation in a convection cell is
a fairly subtle matter (see, e.g.,
Getling [1998] for a
survey of some situations related to convection in horizontal
layers), so that agreement or disagreement between our model and
any really observed pattern can in no way be an indication for the
factors responsible for the observed direction of convective
motions. Our primary interest in the cases where an upwelling is
present in the central part of a cell is merely dictated by our
intention of constructing a dynamo model reproducing the solar
phenomena as closely as possible.
3.2. Heating "From Outside" (Through the Inner Surface)
[35] In addition, we undertook a search for regimes in which convection
preserves its "three-dimensional" structure in the absence of
internal heat sources. In other words, some computations were done
at
Ri=0. The quadratic term was also missing from the
temperature dependence of density ( 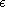 = 0 ) in these runs.
= 0 ) in these runs.
[36] Note that, in the limiting case of a nonrotating shell, convection
cells are not stretched in any direction. Therefore, a cellular
pattern of convective motion can obviously be maintained even
without such favorable factors as a specific form of
stratification and a quadratic term, but at smaller rotational
velocities.
[37] In shells without internal heat sources ( q=0 ), convection
regimes similar to those observed at
q 0 should be expected,
under otherwise identical conditions, at smaller
h. This is
because a stratification similar to that shown in Figure 2
confines the development of convective motion to the outer part of
the shell.

|
|
Figure 10
|
[38] We illustrate here the case of
q=0 only by a tentative
computational run for convection without a magnetic field, at
h=0.9,
P=1,
t=0.1,
Re = 5000, and
m0=2 (see Figure 10 for a velocity field typical of this case).
Although the convection pattern is complex in this case, a
tendency toward the formation of meridionally elongated cells can
nevertheless be noted.
[39] Computations with the magnetic field included (e.g., for
h=0.8,
P=1,
Re=5000,
t=0.1,
Pm=5 )
demonstrate the development of magnetic features with a very small
spatial scale, close to the resolution limit of the computational
scheme. This is a signature for an insufficient spatial
resolution, so that the simulation results are not quite reliable.
[40] The qualitative aspects of the results suggest that the Coriolis
number proves again to be insufficiently small for the stability
of "three-dimensional" convection cells, and the cells
ultimately become substantially stretched, although not in a
strictly meridional direction.
[41] On the whole, the last two scenarios of flow and magnetic field
evolution indicate that regimes of "cellular" dynamo in a shell
without internal heating and without a quadratic term in the
r(T) dependence should be sought in the range of smaller
W (and
t ).

Powered by TeXWeb (Win32, v.2.0).
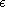 =0.005.
=0.005.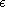 =0.005.
=0.005.






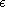 =0 ) and by the Coriolis number
( t=1 ); in addition, we assumed
m0=1 in this case.
=0 ) and by the Coriolis number
( t=1 ); in addition, we assumed
m0=1 in this case.

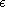 = 0 ) in these runs.
= 0 ) in these runs.

