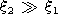* equation (8)
has both periodic solutions and one nonperiodic solution (a
soliton). The critical value
Mi =M* satisfies the known equation
The solution of this equation provides the value
M* 1.6.
1.6.
[10] Under
Mi >M*  1.6,
the solution in the form of a soliton is
absent. This property is typical only for the case of a strong
nonlinearity. At the presence of a weak nonlinearity, there is no
such critical parameter
Mi =M* (see, for example, stationary
solution of the Korteweg-de Vries equations). At a transition from
the value
Mi =1 to the limiting value
Mi =M*,
there occurs an
increase of the amplitude of soliton
Y from zero up to
Y* = Mi2/2.
In this case a limiting value of the ion component velocity
Vi = M* V s is reached.
1.6,
the solution in the form of a soliton is
absent. This property is typical only for the case of a strong
nonlinearity. At the presence of a weak nonlinearity, there is no
such critical parameter
Mi =M* (see, for example, stationary
solution of the Korteweg-de Vries equations). At a transition from
the value
Mi =1 to the limiting value
Mi =M*,
there occurs an
increase of the amplitude of soliton
Y from zero up to
Y* = Mi2/2.
In this case a limiting value of the ion component velocity
Vi = M* V s is reached.
[11] We take into account simultaneous influence of collisions
( ni 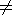 0 )
and dispersion
( De
0 )
and dispersion
( De 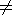 0 )
under the condition
Te
0 )
under the condition
Te 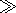 Ti. To do that,
we use the relation between
Y and
Vi:
Ti. To do that,
we use the relation between
Y and
Vi:
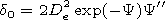 | (10) |
We perform the analysis under the condition of a smallness of the
d0 parameter. We use the presentation
Y|De=0= - ln(1- Vi c-1 )
and obtain the approximate description
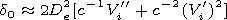 | (11) |
Idealization
De=0 corresponds to the long-wave approximation
for ion-sonic description of the condition
De 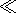 l ( l is the spatial
scale of field disturbances).
l ( l is the spatial
scale of field disturbances).
[12] Using (10) and (11) we obtain the following formulae:
These formulae make it possible on the basis of equation (6) to
obtain an approximate equation for the velocity of the plasma ion
component
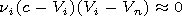 | (12) |
The terms of the second order on
Vi and first order on the
parameter
De2 are left in equation (12).
Pavlov [1996]
obtained
equation (16) for the function
Vi taking into account the ion viscosity and heat conductivity. With the help of equation (12) we are able estimate the order of magnitude of the length scale
L
[13] Taking into account equation (12), we obtain a description of the process in
the problem of the Stage 1 for the dimensionless functions
V=Vi/c
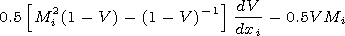 | (13) |
where
xi= x1-1( x-ct),
x1= V sn-1,
d=De x1-1,
A= 0.5(5)1/2Ti Te-1 is the dimensionless coefficient of
the ion viscosity,
Mi = cV s-1 is the Mach ion number. In the
stationary wave, there is a presentation for the dimensionless ion
concentration
n=ni/n0i = (1-V)-1 (here the zero index means
undisturbed state). Equation (13) is obtained assuming that the
influence of charges on neutral particles is negligible.
Under some particular conditions, a formation of regions with
increased ionization degree is possible. Those are the regions of
strong influence of charges on the neutral component
and the shock wave itself. In this very situation the Stage 2 is
realized.
[14] Equation (13) is of the third degree. To solve this equation, one has
to formulate three boundary conditions. At analytical solution, one
condition is put at the infinity behind the shock wavefront:
V( ) =0 which corresponds to the limiting transition to the
undisturbed condition. Two more conditions should provide a
joining of the fields at the front. They may be obtained from the
solution of the closed problem in the region behind the front
(xi<0). Not doing that, we formulate the second condition
approximately. Assuming an idealization of the complete carrying
away of charges by the front a strong shock wave, we obtain the
condition
V(0)
) =0 which corresponds to the limiting transition to the
undisturbed condition. Two more conditions should provide a
joining of the fields at the front. They may be obtained from the
solution of the closed problem in the region behind the front
(xi<0). Not doing that, we formulate the second condition
approximately. Assuming an idealization of the complete carrying
away of charges by the front a strong shock wave, we obtain the
condition
V(0)  2 (g+1)-1,
g
2 (g+1)-1,
g 1.4 being the ratio of the specific
heat capacities. At this approximated approach, the formulation of
the third condition presents some difficulties and its choice may be
ambiguous. For example, the rule of selection of the solution by
some sign may be such condition.
1.4 being the ratio of the specific
heat capacities. At this approximated approach, the formulation of
the third condition presents some difficulties and its choice may be
ambiguous. For example, the rule of selection of the solution by
some sign may be such condition.
[15] Integrating equation (13) numerically (for example, by the Runge-Kutta
method), one has to give all three boundary conditions in the
initial point
xi=0, but in such a way that at
xi 
 there
occurred the transition
V
there
occurred the transition
V  0. Thus, two conditions on the
derivatives
V'(0) and
V''(0) should simultaneously provide the
limiting transition to the undisturbed state and the rule of the
solution selection.
0. Thus, two conditions on the
derivatives
V'(0) and
V''(0) should simultaneously provide the
limiting transition to the undisturbed state and the rule of the
solution selection.
[16] It should be noted that at
d=0 and
A=0,
(13) is transformed into
an equation of the first order, but the solution of the physical
problem should fulfill two boundary conditions:
V(0) and
V( ).
In
the case
Mi<1, there exists a continuous solution, whereas at
Mi>1, the condition at the infinity
V(
).
In
the case
Mi<1, there exists a continuous solution, whereas at
Mi>1, the condition at the infinity
V(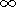 ) may be fulfilled only
due to introduction of a break
[Pavlov, 1996].
The influence of the
dispersion
d
) may be fulfilled only
due to introduction of a break
[Pavlov, 1996].
The influence of the
dispersion
d 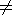 0 and viscosity
A>0 leads to a smoothing of the
break in the plasma precursor.
0 and viscosity
A>0 leads to a smoothing of the
break in the plasma precursor.
|
|
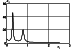
Figure 1
|
|
|
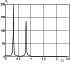
Figure 2
|
|
|
Figure 3
|
|
|
Figure 4
|
|
|
Figure 5
|

|
|
Figure 6
|
[17] The analytical estimates
[Pavlov, 2000]
and the results of numerical
simulations
[Pavlov, 2002a]
showed that a specific ion-sonic wave
is formed in the precursor. Figures 1, 2, 3, 4, 5, and 6 show the new computer
results of the author based on (13) for the plasma parameters
corresponding to undisturbed state typical for a laboratory ballistic
experiment
[Klimov et al., 1982;
Mishin et al., 1991]:
 | (14) |
and for the Mach ion numbers in the range
Mi = 1.7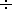 1.94.
We
note the most interesting properties of the plasma precursor of a
shock wave. For the chosen version of the undisturbed plasma
parameters in the Mach ion numbers
Mi = 1.7 < 1.92,
in the
precursor there are two maxima of the ion concentration. They are
two solitons. The soliton most distant from the point
xi=0 provides a "smoothing" of the brake at the front of the ion-sonic
precursor. Under fulfillment of the condition
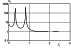
Mi = 1.7 < 1.85
(see
Figures 1 and 2), the largest of the solitons is located closer to the
front of the shock wave
xi=0.
Under
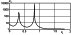
Mi>1.86
(see Figures 3 and 4), the structure of the disturbance
changes: the smaller of the
solitons is located closer to the shock wavefront (the largest of the
maxima moves to the front edge of the precursor). Then there
happens a further sharp change in the structure: at
Mi
1.94.
We
note the most interesting properties of the plasma precursor of a
shock wave. For the chosen version of the undisturbed plasma
parameters in the Mach ion numbers
Mi = 1.7 < 1.92,
in the
precursor there are two maxima of the ion concentration. They are
two solitons. The soliton most distant from the point
xi=0 provides a "smoothing" of the brake at the front of the ion-sonic
precursor. Under fulfillment of the condition
Mi = 1.7 < 1.85
(see
Figures 1 and 2), the largest of the solitons is located closer to the
front of the shock wave
xi=0.
Under
Mi>1.86
(see Figures 3 and 4), the structure of the disturbance
changes: the smaller of the
solitons is located closer to the shock wavefront (the largest of the
maxima moves to the front edge of the precursor). Then there
happens a further sharp change in the structure: at
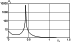
Mi  1.92 there
is formed one maximum (see Figure 5). Further on at
Mi
1.92 there
is formed one maximum (see Figure 5). Further on at
Mi  1.94 (see Figure 6), a "destruction" of this plasma coagulum occurs and
a ion concentration disturbance changing in a monotonous way is
formed. The dimensionless spatial scale of the plasma precursor is
of the order of the unity (this spatial scale has a value of the order
of
x1
1.94 (see Figure 6), a "destruction" of this plasma coagulum occurs and
a ion concentration disturbance changing in a monotonous way is
formed. The dimensionless spatial scale of the plasma precursor is
of the order of the unity (this spatial scale has a value of the order
of
x1  nin V s ).
An increase of the shock front velocity leads to a
decrease of the dimension of the precursor (see Figures 1-5).
nin V s ).
An increase of the shock front velocity leads to a
decrease of the dimension of the precursor (see Figures 1-5).
[18] Thus, the shock wave precursor has an oscillating structure (it can
have several maxima). The precursor has nonlinear resonance
properties relative to the motion velocity
c. Depending on the
plasma parameters in the undisturbed condition, the maximum
values of the disturbance are reached at different values of the
shock wave velocity in the range
c (1.6
(1.6 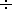 2)V s
2)V s  c*.
The only
maximally dense local coagulum of charged particles is formed in
the precursor (in the considered version it occurs under
c
c*.
The only
maximally dense local coagulum of charged particles is formed in
the precursor (in the considered version it occurs under
c  1.93 V s,
see Figure 5). If the shock wave exceeds the critical velocity
c*, a
collapse of this plasma coagulum occurs (see Figure 6). It is
interesting that even the presence of a strong dissipation does not
destroy the sharp resonance nonlinear effect. The nature of this
effect is due to the rivaling of strong nonlinearity, strong
dispersion, and dissipation.
1.93 V s,
see Figure 5). If the shock wave exceeds the critical velocity
c*, a
collapse of this plasma coagulum occurs (see Figure 6). It is
interesting that even the presence of a strong dissipation does not
destroy the sharp resonance nonlinear effect. The nature of this
effect is due to the rivaling of strong nonlinearity, strong
dispersion, and dissipation.
[19] The gas in this coagulum is no more a weakly ionized one, and
charged particles may influence on the
neutral component and shock wave.
2.2. Solution Stage 2
[20] The disturbance in the neutral component presents the main
interest for practical applications. The solution of the closed
problem, taking into account simultaneous mutual influence of
neutral and charged particles on each other, at the current stage
meets considerable difficulties. We obtain a criterion of strong
interaction of the local coagulum of charged components of weakly
ionized plasma (in means that the plasma is weakly ionized in
undisturbed conditions) with its neutral component and estimate the
spatial scale of the neutral component disturbance. We will study
here only one of possible mechanisms of realization of such
possibility: interaction of charged particles with neutral particles via
elastic collisions. We obtain the necessary condition of such strong
influence for the particular case of stationary situation. Our
consideration will be limited by one-dimensional fields. We
describe the processes in the weakly ionized nonisothermal plasma
by the system of gasdynamics equations (1)-(5). The continuity
equation (1) at
j=n and equation of motion (5) take into account
the retroaction impact of charged particles on the neutral ones. In
the stationary regime, from continuity equation (1), there follows a
relation between the disturbances in the neutral component
concentration and its velocity
 | (15) |
If the regime of weak nonlinearity
(Vn/c)  (a/c) = M-1 is realized, the
concentration disturbances are also weak and there exists an
estimate of the disturbance value
Only in the case of strong nonlinearity
Vn
(a/c) = M-1 is realized, the
concentration disturbances are also weak and there exists an
estimate of the disturbance value
Only in the case of strong nonlinearity
Vn 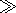 a, considerable
disturbances of the neutral component are possible. For the
stationary supersonic regime, this conclusion is of a general,
universal character: it does not depend on the method of influence
on the neutral component. The value of the nonlinearity may be
characterized by the parameter
(Vn/a) =K. According to (15) we
have a relation making it possible to estimate the value of the
disturbances
In the stationary regime, there exists a formula based on equations
(1)-(5) and relating the fields
a, considerable
disturbances of the neutral component are possible. For the
stationary supersonic regime, this conclusion is of a general,
universal character: it does not depend on the method of influence
on the neutral component. The value of the nonlinearity may be
characterized by the parameter
(Vn/a) =K. According to (15) we
have a relation making it possible to estimate the value of the
disturbances
In the stationary regime, there exists a formula based on equations
(1)-(5) and relating the fields
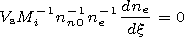 | (16) |
In the case of formation of regions with increased concentration of
charged particles leading to a strong influence on the neutral
component, the first two terms in (16) should be of the same order
as the last term in (16). We compare the order of magnitude of the
first and last terms in (16):
Inside the coagulum formation of a region with increased
ionization degree is possible, therefore there is possible an
appearance of a strong impact of the charges on the plasma neutral
component. It occurs within a narrow range of the Mach ion
numbers
Mi. In the considered situation (14), this occurs at
Mi  1.92 (we remind that the value
M*
1.92 (we remind that the value
M*  1.6 was at
ni=0 a
critical value of the Mach ion-sonic number for the existence of the
soliton). The effect is realized in a resonance way. In spite of the
small spatial scale of the ion-sonic precursor (it is of the order of
the free path of the ion at its motion with the velocity of ion sound
between collisions), such precursor is able to lead to large spatial
disturbances of the neutral component. We estimate the value of
the spatial scale of this disturbance. The spatial scale of the neutral
component disturbance
x2 may be estimated on the basis of the
comparison of separate terms in the equation of motion (5):
We obtain the estimate
a2 x2-1
1.6 was at
ni=0 a
critical value of the Mach ion-sonic number for the existence of the
soliton). The effect is realized in a resonance way. In spite of the
small spatial scale of the ion-sonic precursor (it is of the order of
the free path of the ion at its motion with the velocity of ion sound
between collisions), such precursor is able to lead to large spatial
disturbances of the neutral component. We estimate the value of
the spatial scale of this disturbance. The spatial scale of the neutral
component disturbance
x2 may be estimated on the basis of the
comparison of separate terms in the equation of motion (5):
We obtain the estimate
a2 x2-1  nni Vn, where
aVn-1
is the value of
the order of the unity. Thus, in plasma there will be formed a
disturbed region of the neutral component with the spatial scale
where
The parameter
x1
nni Vn, where
aVn-1
is the value of
the order of the unity. Thus, in plasma there will be formed a
disturbed region of the neutral component with the spatial scale
where
The parameter
x1  ninV s is a spatial scale of the disturbance of the
ion component at the absence of influence of the
charges on the neutral component.
The retroaction impact of the charges on the
neutral component leads to a significant "stretching" of the
precursor of the shock wave. For situation (14) a condition of
strong difference in the spatial scales is realized:
At the presence of a strong influence of the charges on the neutral
component, the spatial scale of the disturbed neutral component is
characterized by the value
a nni-1 (here
nni is the frequency of ion-neutral
collisions). Outside the resonance region, the influence of
the charges on the neutral component is weak.
ninV s is a spatial scale of the disturbance of the
ion component at the absence of influence of the
charges on the neutral component.
The retroaction impact of the charges on the
neutral component leads to a significant "stretching" of the
precursor of the shock wave. For situation (14) a condition of
strong difference in the spatial scales is realized:
At the presence of a strong influence of the charges on the neutral
component, the spatial scale of the disturbed neutral component is
characterized by the value
a nni-1 (here
nni is the frequency of ion-neutral
collisions). Outside the resonance region, the influence of
the charges on the neutral component is weak.

Powered by TeXWeb (Win32, v.2.0).
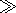 Ti
Ti  Tn generated by a strong
shock wave of neutral component. We take this wave in a form
Tn generated by a strong
shock wave of neutral component. We take this wave in a form
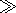 Ti
Ti  Tn generated by a strong
shock wave of neutral component. We take this wave in a form
Tn generated by a strong
shock wave of neutral component. We take this wave in a form
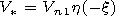


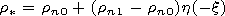

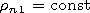
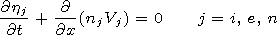
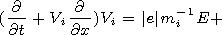
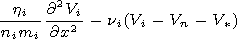
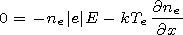
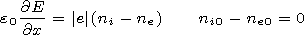
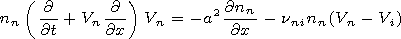
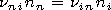
 ,
Vj(
,
Vj( 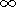 ) =0,
nj(
) =0,
nj( 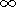 ) =nj0,
E(
) =nj0,
E( 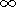 ) =0 were used.
) =0 were used.
 ni0nn0-1
ni0nn0-1 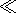 1.
This fact makes it possible to
simplify the description of the process of interaction of the shock
wave with plasma components. Solving the problem at the first stage,
a step-by-step consideration of the process is possible for obtaining
estimates. Taking into account weak ionization of the plasma, we
first neglect the retroaction of charged components on the plasma
neutral components.
1.
This fact makes it possible to
simplify the description of the process of interaction of the shock
wave with plasma components. Solving the problem at the first stage,
a step-by-step consideration of the process is possible for obtaining
estimates. Taking into account weak ionization of the plasma, we
first neglect the retroaction of charged components on the plasma
neutral components.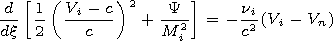

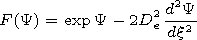
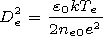
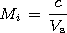
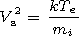
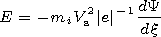
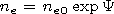
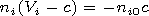
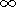 ,
Vj(
,
Vj( 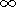 ) =0,
nj(
) =0,
nj( 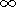 ) =nj0,
Y(
) =nj0,
Y( 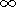 ) =0, and
j=i,e
were used. To clarify the field properties, it is useful to
analyze various limiting situations.
) =0, and
j=i,e
were used. To clarify the field properties, it is useful to
analyze various limiting situations.
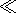 L2 ( De2 is a small parameter in the approximation
of long waves,
L is a special scale of the fields variation). The order
of magnitude of
L can be estimated later after receiving equation (12) by comparison of the first two
terms in this equation:
L2 ( De2 is a small parameter in the approximation
of long waves,
L is a special scale of the fields variation). The order
of magnitude of
L can be estimated later after receiving equation (12) by comparison of the first two
terms in this equation:
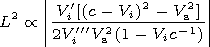
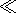 L2 corresponds to the
description of slowly changing fields with neglecting the highest
derivatives in the system of equations (neglecting the effect of
dispersion). Such consideration is not satisfactory in the vicinity of
fronts, because there exists sharp field gradients. In the vicinity of
fronts, the role of highest derivatives is significant and one has to
introduce a corresponding specification. In the long-wave
approximation
De2
L2 corresponds to the
description of slowly changing fields with neglecting the highest
derivatives in the system of equations (neglecting the effect of
dispersion). Such consideration is not satisfactory in the vicinity of
fronts, because there exists sharp field gradients. In the vicinity of
fronts, the role of highest derivatives is significant and one has to
introduce a corresponding specification. In the long-wave
approximation
De2 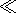 L2 at the increase of the Mach number
Mi up to the unity, there occurs an increase of the field gradients in the
precursor. In the
Mi=1 situation, there is formed a discontinuity
in the first derivatives (weak discontinuity) in some point
x= x* [Pavlov, 1996].
This is caused by the absence of a continuous
solution satisfying the boundary condition at
x=
L2 at the increase of the Mach number
Mi up to the unity, there occurs an increase of the field gradients in the
precursor. In the
Mi=1 situation, there is formed a discontinuity
in the first derivatives (weak discontinuity) in some point
x= x* [Pavlov, 1996].
This is caused by the absence of a continuous
solution satisfying the boundary condition at
x= 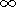 . At
Mi>1 and
De2
. At
Mi>1 and
De2 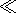 L2,
a discontinuous solution is formed. The value of the
jump in the ion component velocity at the front is
c(1-Mi-2) [Pavlov, 1996].
L2,
a discontinuous solution is formed. The value of the
jump in the ion component velocity at the front is
c(1-Mi-2) [Pavlov, 1996].
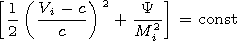
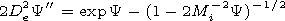

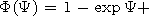
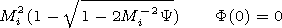
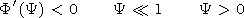
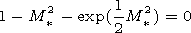
 1.6.
1.6.
 1.6,
the solution in the form of a soliton is
absent. This property is typical only for the case of a strong
nonlinearity. At the presence of a weak nonlinearity, there is no
such critical parameter
Mi =M* (see, for example, stationary
solution of the Korteweg-de Vries equations). At a transition from
the value
Mi =1 to the limiting value
Mi =M*,
there occurs an
increase of the amplitude of soliton
Y from zero up to
Y* = Mi2/2.
In this case a limiting value of the ion component velocity
Vi = M* V s is reached.
1.6,
the solution in the form of a soliton is
absent. This property is typical only for the case of a strong
nonlinearity. At the presence of a weak nonlinearity, there is no
such critical parameter
Mi =M* (see, for example, stationary
solution of the Korteweg-de Vries equations). At a transition from
the value
Mi =1 to the limiting value
Mi =M*,
there occurs an
increase of the amplitude of soliton
Y from zero up to
Y* = Mi2/2.
In this case a limiting value of the ion component velocity
Vi = M* V s is reached.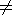 0 )
and dispersion
( De
0 )
and dispersion
( De 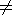 0 )
under the condition
Te
0 )
under the condition
Te 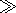 Ti. To do that,
we use the relation between
Y and
Vi:
Ti. To do that,
we use the relation between
Y and
Vi:
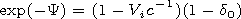
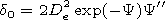
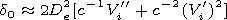
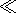 l ( l is the spatial
scale of field disturbances).
l ( l is the spatial
scale of field disturbances).
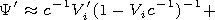
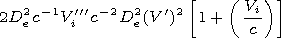

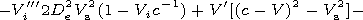
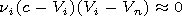
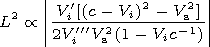

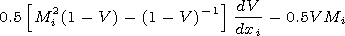
 ) =0 which corresponds to the limiting transition to the
undisturbed condition. Two more conditions should provide a
joining of the fields at the front. They may be obtained from the
solution of the closed problem in the region behind the front
(xi<0). Not doing that, we formulate the second condition
approximately. Assuming an idealization of the complete carrying
away of charges by the front a strong shock wave, we obtain the
condition
V(0)
) =0 which corresponds to the limiting transition to the
undisturbed condition. Two more conditions should provide a
joining of the fields at the front. They may be obtained from the
solution of the closed problem in the region behind the front
(xi<0). Not doing that, we formulate the second condition
approximately. Assuming an idealization of the complete carrying
away of charges by the front a strong shock wave, we obtain the
condition
V(0)  2 (g+1)-1,
g
2 (g+1)-1,
g 1.4 being the ratio of the specific
heat capacities. At this approximated approach, the formulation of
the third condition presents some difficulties and its choice may be
ambiguous. For example, the rule of selection of the solution by
some sign may be such condition.
1.4 being the ratio of the specific
heat capacities. At this approximated approach, the formulation of
the third condition presents some difficulties and its choice may be
ambiguous. For example, the rule of selection of the solution by
some sign may be such condition.
 there
occurred the transition
V
there
occurred the transition
V  0. Thus, two conditions on the
derivatives
V'(0) and
V''(0) should simultaneously provide the
limiting transition to the undisturbed state and the rule of the
solution selection.
0. Thus, two conditions on the
derivatives
V'(0) and
V''(0) should simultaneously provide the
limiting transition to the undisturbed state and the rule of the
solution selection.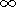 ).
In
the case
Mi<1, there exists a continuous solution, whereas at
Mi>1, the condition at the infinity
V(
).
In
the case
Mi<1, there exists a continuous solution, whereas at
Mi>1, the condition at the infinity
V(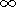 ) may be fulfilled only
due to introduction of a break
[Pavlov, 1996].
The influence of the
dispersion
d
) may be fulfilled only
due to introduction of a break
[Pavlov, 1996].
The influence of the
dispersion
d 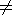 0 and viscosity
A>0 leads to a smoothing of the
break in the plasma precursor.
0 and viscosity
A>0 leads to a smoothing of the
break in the plasma precursor.






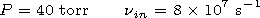

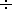 1.94.
We
note the most interesting properties of the plasma precursor of a
shock wave. For the chosen version of the undisturbed plasma
parameters in the Mach ion numbers
Mi = 1.7 < 1.92,
in the
precursor there are two maxima of the ion concentration. They are
two solitons. The soliton most distant from the point
xi=0 provides a "smoothing" of the brake at the front of the ion-sonic
precursor. Under fulfillment of the condition
Mi = 1.7 < 1.85
(see
Figures 1 and 2), the largest of the solitons is located closer to the
front of the shock wave
xi=0.
Under
Mi>1.86
(see Figures 3 and 4), the structure of the disturbance
changes: the smaller of the
solitons is located closer to the shock wavefront (the largest of the
maxima moves to the front edge of the precursor). Then there
happens a further sharp change in the structure: at
Mi
1.94.
We
note the most interesting properties of the plasma precursor of a
shock wave. For the chosen version of the undisturbed plasma
parameters in the Mach ion numbers
Mi = 1.7 < 1.92,
in the
precursor there are two maxima of the ion concentration. They are
two solitons. The soliton most distant from the point
xi=0 provides a "smoothing" of the brake at the front of the ion-sonic
precursor. Under fulfillment of the condition
Mi = 1.7 < 1.85
(see
Figures 1 and 2), the largest of the solitons is located closer to the
front of the shock wave
xi=0.
Under
Mi>1.86
(see Figures 3 and 4), the structure of the disturbance
changes: the smaller of the
solitons is located closer to the shock wavefront (the largest of the
maxima moves to the front edge of the precursor). Then there
happens a further sharp change in the structure: at
Mi  1.92 there
is formed one maximum (see Figure 5). Further on at
Mi
1.92 there
is formed one maximum (see Figure 5). Further on at
Mi  1.94 (see Figure 6), a "destruction" of this plasma coagulum occurs and
a ion concentration disturbance changing in a monotonous way is
formed. The dimensionless spatial scale of the plasma precursor is
of the order of the unity (this spatial scale has a value of the order
of
x1
1.94 (see Figure 6), a "destruction" of this plasma coagulum occurs and
a ion concentration disturbance changing in a monotonous way is
formed. The dimensionless spatial scale of the plasma precursor is
of the order of the unity (this spatial scale has a value of the order
of
x1  nin V s ).
An increase of the shock front velocity leads to a
decrease of the dimension of the precursor (see Figures 1-5).
nin V s ).
An increase of the shock front velocity leads to a
decrease of the dimension of the precursor (see Figures 1-5). (1.6
(1.6  2)V s
2)V s  c*.
The only
maximally dense local coagulum of charged particles is formed in
the precursor (in the considered version it occurs under
c
c*.
The only
maximally dense local coagulum of charged particles is formed in
the precursor (in the considered version it occurs under
c  1.93 V s,
see Figure 5). If the shock wave exceeds the critical velocity
c*, a
collapse of this plasma coagulum occurs (see Figure 6). It is
interesting that even the presence of a strong dissipation does not
destroy the sharp resonance nonlinear effect. The nature of this
effect is due to the rivaling of strong nonlinearity, strong
dispersion, and dissipation.
1.93 V s,
see Figure 5). If the shock wave exceeds the critical velocity
c*, a
collapse of this plasma coagulum occurs (see Figure 6). It is
interesting that even the presence of a strong dissipation does not
destroy the sharp resonance nonlinear effect. The nature of this
effect is due to the rivaling of strong nonlinearity, strong
dispersion, and dissipation.
 (a/c) = M-1 is realized, the
concentration disturbances are also weak and there exists an
estimate of the disturbance value
(a/c) = M-1 is realized, the
concentration disturbances are also weak and there exists an
estimate of the disturbance value
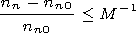
 a, considerable
disturbances of the neutral component are possible. For the
stationary supersonic regime, this conclusion is of a general,
universal character: it does not depend on the method of influence
on the neutral component. The value of the nonlinearity may be
characterized by the parameter
(Vn/a) =K. According to (15) we
have a relation making it possible to estimate the value of the
disturbances
a, considerable
disturbances of the neutral component are possible. For the
stationary supersonic regime, this conclusion is of a general,
universal character: it does not depend on the method of influence
on the neutral component. The value of the nonlinearity may be
characterized by the parameter
(Vn/a) =K. According to (15) we
have a relation making it possible to estimate the value of the
disturbances
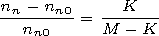
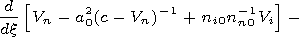
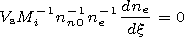
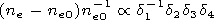


 1.92 (we remind that the value
M*
1.92 (we remind that the value
M*  1.6 was at
ni=0 a
critical value of the Mach ion-sonic number for the existence of the
soliton). The effect is realized in a resonance way. In spite of the
small spatial scale of the ion-sonic precursor (it is of the order of
the free path of the ion at its motion with the velocity of ion sound
between collisions), such precursor is able to lead to large spatial
disturbances of the neutral component. We estimate the value of
the spatial scale of this disturbance. The spatial scale of the neutral
component disturbance
x2 may be estimated on the basis of the
comparison of separate terms in the equation of motion (5):
1.6 was at
ni=0 a
critical value of the Mach ion-sonic number for the existence of the
soliton). The effect is realized in a resonance way. In spite of the
small spatial scale of the ion-sonic precursor (it is of the order of
the free path of the ion at its motion with the velocity of ion sound
between collisions), such precursor is able to lead to large spatial
disturbances of the neutral component. We estimate the value of
the spatial scale of this disturbance. The spatial scale of the neutral
component disturbance
x2 may be estimated on the basis of the
comparison of separate terms in the equation of motion (5):
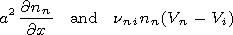
 nni Vn, where
aVn-1
is the value of
the order of the unity. Thus, in plasma there will be formed a
disturbed region of the neutral component with the spatial scale
nni Vn, where
aVn-1
is the value of
the order of the unity. Thus, in plasma there will be formed a
disturbed region of the neutral component with the spatial scale
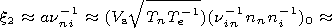
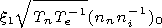
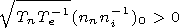
 ninV s is a spatial scale of the disturbance of the
ion component at the absence of influence of the
charges on the neutral component.
The retroaction impact of the charges on the
neutral component leads to a significant "stretching" of the
precursor of the shock wave. For situation (14) a condition of
strong difference in the spatial scales is realized:
ninV s is a spatial scale of the disturbance of the
ion component at the absence of influence of the
charges on the neutral component.
The retroaction impact of the charges on the
neutral component leads to a significant "stretching" of the
precursor of the shock wave. For situation (14) a condition of
strong difference in the spatial scales is realized: