2. Propagation of a Pulse in an Isotropic Plasma
[3] Propagation of the pulse is described by a wave equation
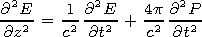 | (1) |
where
E is the electric field strength,
c is the speed of light in the
medium,
z is the direction of propagation,
t is the time, and
P is
the polarization of a unit volume of the medium. In accordance
with the model of the medium with free charges
[Pamyatnykh and Turov, 2000;
Vinogradova et al., 1979],
P is described by
 | (2) |
In equation (2),
e and
m are the charge and mass of an electron,
respectively;
N is the electron concentration, and
n is the
effective collision frequency which takes into account energy
losses by electrons due to collisions with neutral molecules and
ions.
[4] At the boundary of the half-space
z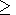 0 where the pulse
propagates, the field
E is written as
0 where the pulse
propagates, the field
E is written as
 | (3) |
Here,
w = 2p f;
f is the carrier frequency; and
A(0;t) is the pulse
envelope at
z=0.
[5] The leading edge of the pulse always propagates with the
velocity of light in the medium. Accordingly, the field
E will be
sought in the form
(k=w/c=2p/l is the wave number)
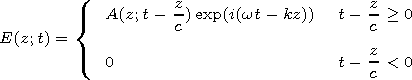 | (4) |
In equations (1) and (2), variables are changed as
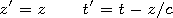 | (5) |
Taking into account equation (4), we get
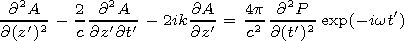 | (6) |
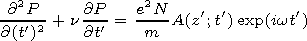 | (7) |
Let us compare the magnitudes of the first and third terms in the
left-hand side of equation (6) for the pulse with a carrier considered
here. Its characteristic duration
tp satisfies the inequality
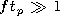 | (8) |
and the pulse itself occupies on the
z' axis the interval
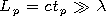 | (9) |
Therefore the estimate
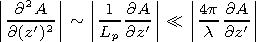 | (10) |
is valid, and the first term in the left-hand side of equation (6) can
be neglected. Note that inequalities (8) and (9) are also fulfilled for
wideband pulses
[Varakin, 1970]
and their special case, i.e., pulses
with a linear frequency modulation. Therefore estimate (10) is valid
for these pulses as well.
[6] Since the position and velocity of an electron cannot change
instantaneously, the conditions
 | (11) |
are fulfilled in cold plasma at the moment of arrival of the pulse at
point
z' . Then the solution of equation (7) is given by
 | (12) |
Let us substitute solution (12) into equation (6). If we take into
account estimate (10), the equation for the pulse envelope
A(z';t) acquires the form
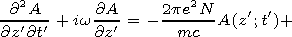 | (13) |
By applying the Laplace transformation with respect to variable
t' to equation (13), we get
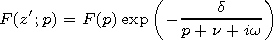 | (14) |
The designations we use here are
is the Laplace image of the initial
envelope;
d = d(z')=w02z'/2c;
w02=4p e2 N/m;
w0 is the
plasma frequency; and it is assumed that
A(z';0)=0. It is evident
that the latter condition is fulfilled for the pulse whose initial
envelope is zero at
t=0
[7] By performing inverse Laplace transformation, we obtain
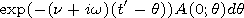 | (15) |
Jk(x) is the Bessel function here and in what follows.
[8] The solution of equation (15) is written for the initial
envelopes which will be used below as examples to illustrate the
character of distortions of radio wave pulses in a cold isotropic
plasma. A biexponential pulse with the envelope in the form
( A0; a; b are the numbers)
 | (16) |
is a good approximation for pulses with different steepness of the
leading and trailing edges. By substituting equation (16) into
equation (15) and changing the variable
m= (q/t')1/2 in the obtained
expression, we get
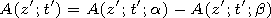 | (17) |
where the
a -dependent term is written as
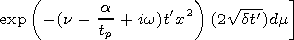 | (18) |
and the term that depends on parameter
b is obtained from
equality (18) by replacing
a by
b.
[9] The initial envelope of the so-called sine wave pulse is
given by
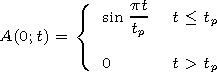 | (19) |
Let us present the envelope (19) in the form
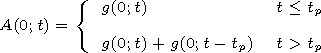 | (20) |
where
and substitute equation (20) into equation (15). By performing the
operations similar to those described above, we obtain the
expressions for a deformable sine wave pulse
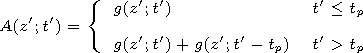 | (21) |
where
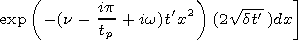 | (22) |
Let us now derive the solution of the problem for a
rectangular pulse
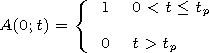 | (23) |
whose distortions, according to equation (23), are described by
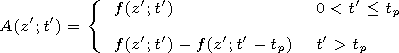 | (24) |
In order to obtain the
f(z';t') function, it should be borne in mind
that when
a 0 and
b
0 and
b 
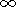 simultaneously, the bi-exponential
pulse transforms into a step pulse of height
A0, the value of
A remaining zero at
t=0. By performing appropriate
transformations in equations (17) and (18), at
t'>0 we get the
envelope of a step pulse in the form
(A0=1)
simultaneously, the bi-exponential
pulse transforms into a step pulse of height
A0, the value of
A remaining zero at
t=0. By performing appropriate
transformations in equations (17) and (18), at
t'>0 we get the
envelope of a step pulse in the form
(A0=1)
 | (25) |
When
t' increases, the problem on the incidence of a step
pulse on a semi-infinite homogeneous medium transforms into the
problem on propagation of a plane wave in a homogeneous
medium. Let us demonstrate that solution (25) satisfies this
requirement. Let us again turn to solution (15), which for a step
pulse acquires the form
It is easy to see that relations (25) and (25a) are equivalent. Let
t'
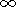 in equation (25a). In this case the integral in the left-hand
side reduces to the tabulated one. Its calculation gives
in equation (25a). In this case the integral in the left-hand
side reduces to the tabulated one. Its calculation gives
Here,
t=g(w)z' is the optical depth, and
g(w)= w02n/w2 c is
the absorption coefficient of the plasma with respect to power at
the carrier frequency (at
n 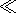 w ).
The first term in equation (25b)
describes a decrease in the amplitude of the plane wave, and the
second term describes an increase in the phase of the plane wave
when it passes a distance
z' [Ginzburg, 1967],
which is what we set
out to prove.
w ).
The first term in equation (25b)
describes a decrease in the amplitude of the plane wave, and the
second term describes an increase in the phase of the plane wave
when it passes a distance
z' [Ginzburg, 1967],
which is what we set
out to prove.

|
|
Figure 1
|

|
|
Figure 2
|

|
|
Figure 3
|
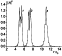
[10] Analysis of the literature on propagation of radio wave
pulses in plasma has revealed, among other things, that a pulse with
a rectangular envelope is most frequently considered as an initial
pulse. For this reason, major attention will be given below to this
type of pulses. Figures 1 and 2 differ only by the durations of the
rectangular pulses; the parameters of the medium are taken to be
approximately corresponding to the conditions in the ionosphere
[Kirillov and Kopeikin, 2003].
In combination, they illustrate the
character of distortions of a pulse caused by, in addition to
tp, the
path length and the absorption effect. At
tp=10-4 s (Figure 1), the
shape of the envelope remains close to a rectangular one up to
considerable distances from the source (~2000 km), and its
distortions manifest themselves in oscillations in the field
magnitude about an average level determined by the optical depth
of the path. Elongation of the path is accompanied by an increase in
the relative amplitude and characteristic period of the oscillations.
As the pulse becomes shorter by an order of magnitude, all other
conditions being equal (Figure 2), the character of distortions of the
envelope appreciably varies and manifests itself now, first of all, in
a pronounced deformation of the leading and trailing fronts. The
fronts gradually spread, and beginning from some distance the
pulse cannot be regarded as rectangular. From the point of view of
the spectral representation, the change in the character of
distortions of the envelope should be attributed to broadening of the
spectrum of the emitted pulse, so that within its limits the
frequency dependences of the refractive index and absorption
coefficient of the medium become appreciably different from the
linear ones. The effect of the rectangular pulse duration on its
distortions can be understood in more detail from Figure 3, in
which curves
|A|2 are compared for four magnitudes of
tp at the
same temporal scale, all other conditions being equal. Figure 3 also
shows that the velocity of propagation of the pulse in plasma is
appreciably
lower than the velocity of light and that the velocity of
propagation of the leading edge of the rectangular pulse is not
determined by the pulse duration. Let us derive an analytical
expression for the pulse propagation velocity. To this end, we use
solution (25). We compute the integral in equation (25) by parts
successively an infinite number of times using the known relation
for Bessel functions
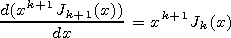 | (26) |
As a result, we get
 | (27) |
We assume that inequality
2(d tp)1/2 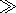 1 is fulfilled, which is typical
of ionospheric paths (see the caption to Figure 1), and use the
asymptotic representation of the Bessel function at large values of
the argument
[Korenev, 1971]
1 is fulfilled, which is typical
of ionospheric paths (see the caption to Figure 1), and use the
asymptotic representation of the Bessel function at large values of
the argument
[Korenev, 1971]
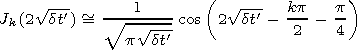 | (28) |
After substitution of equation (28) into equation (27) and
summation of the series obtained in this way, the expression for
A(z';t') acquires the form
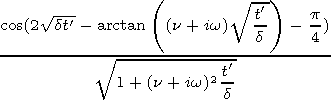 | (29) |
It follows from equation (29) that on the
z' axis the pulse is
concentrated in the vicinity of the point to which the minimum of
the modulus of the radicand in the denominator of the right-hand
side corresponds. The coordinate of this point satisfies the
condition
 | (30) |
from which we infer that the leading edge of the rectangular pulse
propagates with the velocity
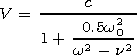 | (31) |
According to equation (31), the effect of collisions can exert an
influence on the propagation velocity if magnitudes of
n are
comparable to the carrier frequency, i.e., only under the conditions
when the propagating pulse is strongly absorbed. For the
parameters of the medium and pulse indicated in the captions to
Figures 1, 2, and 3, the inequality
w2 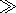 n2 is fulfilled. In this case we
have
n2 is fulfilled. In this case we
have
 | (32) |
|
|
Figure 4
|

|
|
Figure 5
|
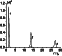
It follows from equation (32) that at a constant path length, all
other conditions being equal, the delay time of a pulse, as
compared with a hypothetical case of its propagation with the
velocity of light, increases with decreasing carrier frequency and
increasing electron concentration. Along with this, solution (25)
takes into account the change in the envelope at the end of the path
caused by variations in the parameters
f and
N indicated
(Figures 4 and 5).
|
|
Figure 6
|
|
|
Figure 7
|
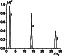
[11] Figures 6 and 7 illustrate the character of distortions of a
bi-exponential pulse (see equation (16)) and sine wave (see equation
(19)) pulse for the parameters of the problem given in the caption
to Figure 2. Comparison of the curves shown in Figures 6 and 7
with the curves presented in Figure 2 leads to the conclusion that in
the case of propagation under similar conditions distortions of both
the bi-exponential and sine wave pulses manifest themselves to a
much lesser degree. From the point of view of the spectral
representation, a reduction in their distortions is naturally
interpreted as the consequence of narrowing of the pulse spectrum
due to smoothing of its initial envelope.

Powered by TeXWeb (Win32, v.2.0).
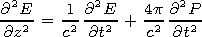
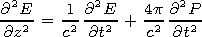

 0 where the pulse
propagates, the field
E is written as
0 where the pulse
propagates, the field
E is written as
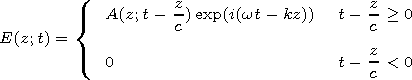
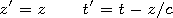
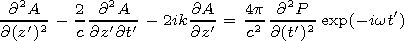
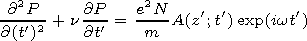
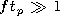
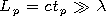
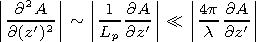


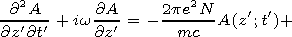
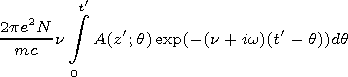
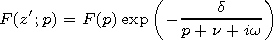

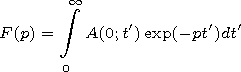
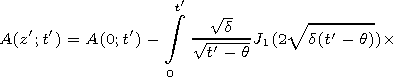
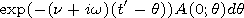

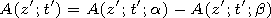

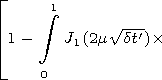
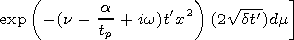
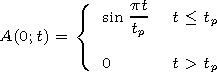
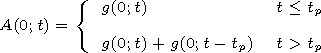
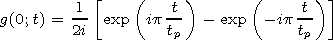
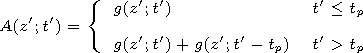
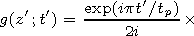
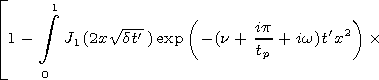
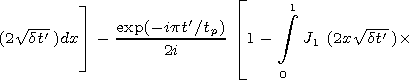
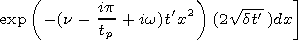
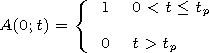
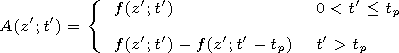
 0 and
b
0 and
b 
 simultaneously, the bi-exponential
pulse transforms into a step pulse of height
A0, the value of
A remaining zero at
t=0. By performing appropriate
transformations in equations (17) and (18), at
t'>0 we get the
envelope of a step pulse in the form
(A0=1)
simultaneously, the bi-exponential
pulse transforms into a step pulse of height
A0, the value of
A remaining zero at
t=0. By performing appropriate
transformations in equations (17) and (18), at
t'>0 we get the
envelope of a step pulse in the form
(A0=1) 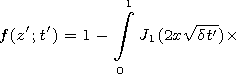

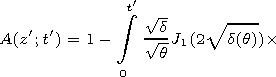


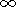 in equation (25a). In this case the integral in the left-hand
side reduces to the tabulated one. Its calculation gives
in equation (25a). In this case the integral in the left-hand
side reduces to the tabulated one. Its calculation gives

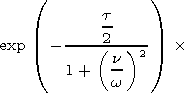
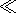 w ).
The first term in equation (25b)
describes a decrease in the amplitude of the plane wave, and the
second term describes an increase in the phase of the plane wave
when it passes a distance
z' [Ginzburg, 1967],
which is what we set
out to prove.
w ).
The first term in equation (25b)
describes a decrease in the amplitude of the plane wave, and the
second term describes an increase in the phase of the plane wave
when it passes a distance
z' [Ginzburg, 1967],
which is what we set
out to prove.



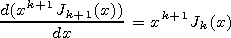


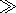 1 is fulfilled, which is typical
of ionospheric paths (see the caption to Figure 1), and use the
asymptotic representation of the Bessel function at large values of
the argument
[Korenev, 1971]
1 is fulfilled, which is typical
of ionospheric paths (see the caption to Figure 1), and use the
asymptotic representation of the Bessel function at large values of
the argument
[Korenev, 1971]
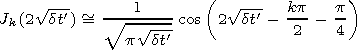
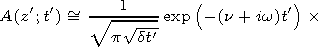
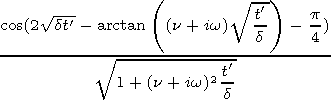
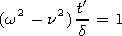
 n2 is fulfilled. In this case we
have
n2 is fulfilled. In this case we
have





