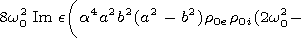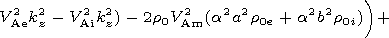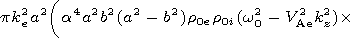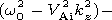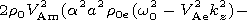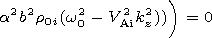|
[2] It is well known that the coronal magnetic flux
tubes are twisted. In addition to the longitudinal
magnetic field they also contain an azimutal component.
The magnetic tubes undergoe expansion in the rarefied
solar atmosphere. If the tube expands, the azimutal
field
Bj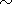 r-1 on the periphery of
the tube is formed. The longitudinal magnetic
field persists only in the central part of the tube
[Parker, 1979].
The mathematical difficulties that arise in describing
of such coronal tube force us to use its crude model
in which the magnetic field has only a longitudinal
component in the central part and only an azimutal
component on the periphery. r-1 on the periphery of
the tube is formed. The longitudinal magnetic
field persists only in the central part of the tube
[Parker, 1979].
The mathematical difficulties that arise in describing
of such coronal tube force us to use its crude model
in which the magnetic field has only a longitudinal
component in the central part and only an azimutal
component on the periphery.
[3] We consider a cylindrical tube of radius
a with
the plasma density
r0m=r0/(ar)2 in which a central part of radius
b (br0i, the other part of the tube is called a shell.
The plasma density in the surrounding corona is
r0e<r0i. The equilibrium magnetic
field has the follow distribution
The Alfvén speeds in the cord and in
the corona are
V Ai, V Ae.
V Am2 =B02/4pr0 is the Alfvén speed scale in the shell.
The equilibrium conditions for the tube are
[4] Let us seek the solutions of linear ideal MHD
equations for the cool plasma in the form of
cylindrical modes
f(r, t)=f(r) exp(imj +i kzz -iwt), where
kz is the longitudinal
wave number and
w is the frequency. They are expressed
through the magnetic pressure perturbation
P(r)=p(r)+ B(r) B0(r)/4p.
The solution in the cord and in the corona
can be expressed in terms of the Bessel equation solutions
(for the kink-mode
m =1):
where
In the thin tube ( kza 1 ) approximation we take the
principal terms of the Bessel and McDonald functions at
r=0.
In the shell the radial equation for
P have the form
[Appert et al., 1974]
Two linearly independent solutions of this
equation have poles of the first and the third orders at
z=0.
The solution in the shell is
where
F and
G are arbitrary constants and
the coefficients have the following approximate expressions
Using the principals terms in the solutions and the boundary conditions
we obtain the dispersion equation in the zeroth order approximation
[Mikhalyaev, 2005]
It should be borne in mind that the tube parameters in this equation
are constrained by equilibrium conditions.
This equation have two real solutions that
describe undamped oscillations. One of them
describes a fast magnetosonic wave whose phase
speed exceeds the Alfvén speed
in the corona. Therefore, it propagates radially
into the surrounding corona, i.e., is radiated by the tube.
The damping manifests itself as the effect of the next order
with respect to the small
kza. In the first approximation,
the dispersion equation has a complex solution with a relatively
small imaginary part. We write the complex frequency as
w=w0(1+ 1 ) approximation we take the
principal terms of the Bessel and McDonald functions at
r=0.
In the shell the radial equation for
P have the form
[Appert et al., 1974]
Two linearly independent solutions of this
equation have poles of the first and the third orders at
z=0.
The solution in the shell is
where
F and
G are arbitrary constants and
the coefficients have the following approximate expressions
Using the principals terms in the solutions and the boundary conditions
we obtain the dispersion equation in the zeroth order approximation
[Mikhalyaev, 2005]
It should be borne in mind that the tube parameters in this equation
are constrained by equilibrium conditions.
This equation have two real solutions that
describe undamped oscillations. One of them
describes a fast magnetosonic wave whose phase
speed exceeds the Alfvén speed
in the corona. Therefore, it propagates radially
into the surrounding corona, i.e., is radiated by the tube.
The damping manifests itself as the effect of the next order
with respect to the small
kza. In the first approximation,
the dispersion equation has a complex solution with a relatively
small imaginary part. We write the complex frequency as
w=w0(1+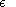 ), where
w0 is the
solution of the dispersion equation in the zeroth order
approximation, and the dimensionless quantity ), where
w0 is the
solution of the dispersion equation in the zeroth order
approximation, and the dimensionless quantity
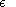 gives the first correction. Its imaginary part determines
the damping coefficient
-w0 Im gives the first correction. Its imaginary part determines
the damping coefficient
-w0 Im 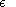 , while
the ratio
Q=-1/2 Im , while
the ratio
Q=-1/2 Im 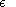 is the
Q-factor of the
oscillations. For is the
Q-factor of the
oscillations. For
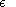 the following expression holds the following expression holds
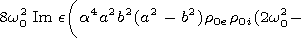 |
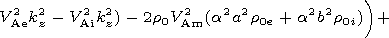 |
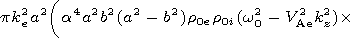 |
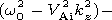 |
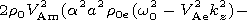 |
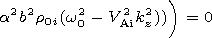 |
[5] We applied the results obtained to the
oscillations of solar coronal loops. As the corona is characterized by
Alfvén speeds much larger than the sound speed, we have
chosen
V Ae=700 km s-1. The density in the cord
r0i=5r0e, and the characteristic density
r0=5r0e was chosen for the shell.
The scale parameter
a =0.25 cm-1. The
Q -factor increases with decreasing wave number,
i.e., with increasing tube length
L. For example,
at the tube radius
a =12 Mm and the cord radius
b =2 Mm, the
Q-factor increases from 19.7 to 84.9 as
the tube length changes from 11 Mm to 230 Mm. The
oscillation period takes on values within the range
239 to 497 s. The Alfvén speed in
the shell is the same, 939 km s-1. The
Q-factor and the period increase with cord radius. If
b changes from 1 to 4 Mm (at
a=12 Mm and
L=130 Mm),
then the period increases from 270 to 328, while the
Q-factor increases from 18.1 to 190.
Our calculations
show that
Q-factors close to their observed values
can be obtained
[Nakariakov et al., 1999;
Ofman and Aschwanden, 2002].
Thus, a double magnetic flux tube with a strongly twisted
magnetic field in the shell can serve as an acceptable model
for coronal loop, and the observed fast damping
of transverse loop oscillations can be explained
in terms of the effective radiation of fast
magnetosonic waves into the surrounding corona by the loop.

Powered by TeXWeb (Win32, v.2.0).
|
 r-1 on the periphery of
the tube is formed. The longitudinal magnetic
field persists only in the central part of the tube
[Parker, 1979].
The mathematical difficulties that arise in describing
of such coronal tube force us to use its crude model
in which the magnetic field has only a longitudinal
component in the central part and only an azimutal
component on the periphery.
r-1 on the periphery of
the tube is formed. The longitudinal magnetic
field persists only in the central part of the tube
[Parker, 1979].
The mathematical difficulties that arise in describing
of such coronal tube force us to use its crude model
in which the magnetic field has only a longitudinal
component in the central part and only an azimutal
component on the periphery.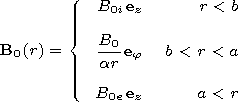
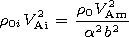
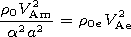
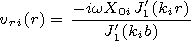
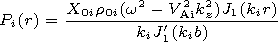
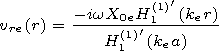
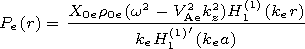
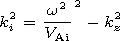
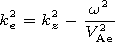
 1 ) approximation we take the
principal terms of the Bessel and McDonald functions at
r=0.
In the shell the radial equation for
P have the form
[Appert et al., 1974]
1 ) approximation we take the
principal terms of the Bessel and McDonald functions at
r=0.
In the shell the radial equation for
P have the form
[Appert et al., 1974]

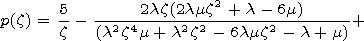

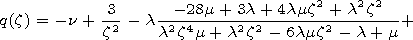
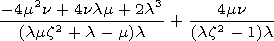
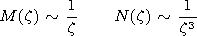
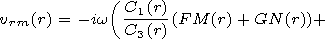
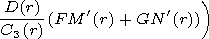
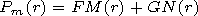
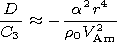
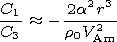
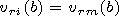
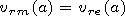

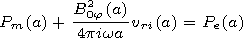
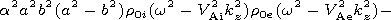
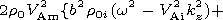
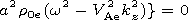
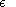 ), where
w0 is the
solution of the dispersion equation in the zeroth order
approximation, and the dimensionless quantity
), where
w0 is the
solution of the dispersion equation in the zeroth order
approximation, and the dimensionless quantity
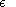 gives the first correction. Its imaginary part determines
the damping coefficient
-w0 Im
gives the first correction. Its imaginary part determines
the damping coefficient
-w0 Im 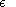 , while
the ratio
Q=-1/2 Im
, while
the ratio
Q=-1/2 Im 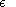 is the
Q-factor of the
oscillations. For
is the
Q-factor of the
oscillations. For
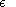 the following expression holds
the following expression holds