3. Formulation of the Problem for a Slot Antenna

|
|
Figure 2
|
[12] Consider an ideally conducting slot antenna having the shape of a
spheroid with the interfocal distance
2d0 and the large and small
semiaxes
a0 and
b0, respectively, located in the medium with the
relative dielectric permeability
e3 and surrounded by a two-layer
plasma coating (Figure 2). The outer surface of the first layer
e1 (the
depleted ion coating) is formed (in the same way as in the first problem)
by the spheroid surface with the interfocal distance
2d1 and semiaxes
a1 and
b1. The second plasma layer
e is limited from the outside
also by the spheroid surface with the interfocal distance
2d and
semiaxes
a and
b. All three spheroids have the same origin of
spheroidal coordinates and equal eccentricities
e.
[13] The solution of the problem for an ideally conducting prolate spheroidal
slot antenna put into a prolate two-layer plasma spheroid will be
constructed in three systems of prolate spheroidal coordinates having the
joint beginning. The slot antenna consists of two metal semispheroids
( x=x0 ) separated by a slot at
|h| < Dh (Dh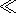 1 ) to which the
voltage
V is applied. According to the commonly accepted statement
[Wait, 1966],
the tangential component of the electric field of the slot
antenna
Eh,
different from zero at the gap, is determined by the
constant value independent of
h
1 ) to which the
voltage
V is applied. According to the commonly accepted statement
[Wait, 1966],
the tangential component of the electric field of the slot
antenna
Eh,
different from zero at the gap, is determined by the
constant value independent of
h
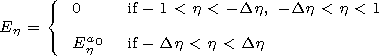 | (7) |
At a small width of the gap
2Dh,
this value is related to the voltage
V by the formula
The solution of the Maxwell equations in the outer medium
e3 satisfying
the principle of emission at the infinity will take the same form (1) as in
the first problem.
[14] In the region of the depleted ion layer
e1, the solution will be
constructed (contrary to the first problem) using two systems of
functions determined in the coordinate systems related to the inner and
intermediate spheroids:
 | (8) |
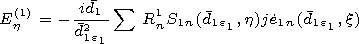 | (9) |
here 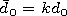 and
and 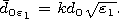
[15] In the region of the plasma layer with the relative dielectric permeability
e,
the solution (in the same way as in the first problem) will take the
form (4)-(5).
[16] At the presence of the boundary
x=x1 at the spheroid surrounding the
slot antenna, to find
An one should to equate the electrical components
of the field (7), (8) and (9) on the surface of the inner spheroid
x= x0 preliminarily reexpanding system of functions (9) over the system of
spheroidal functions (8) with the help of the theorem of addition. As a
result, we obtain the infinite system of related algebraic equations.
Confining ourselves by the main first term in the expansion with
allowance for small parameters 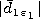 and
and 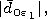 we obtain the
solution of the unrelated equation system in the form of the following
relation for the coefficients of expansions (8) and (9)
we obtain the
solution of the unrelated equation system in the form of the following
relation for the coefficients of expansions (8) and (9)
 | (10) |
where the normalizing multiplier for the angular functions
N1n for
n=1 has the representation
at small 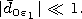 The harmonics with
n>1 in (8) have the amplitudes
An of the smaller
order
O(|d0e1n+1|) as compared to
n=1 and will not be taken into
account below.
The harmonics with
n>1 in (8) have the amplitudes
An of the smaller
order
O(|d0e1n+1|) as compared to
n=1 and will not be taken into
account below.
[17] Reexpanding in the same way the system of functions (5) over the
system (4), presenting the angular functions of the plasma medium in the
form of the expansion over the angular functions of the inner and outer
medium, and confining ourselves by the main terms of the expansions,
we obtain for the boundary conditions the same system of four algebraic
equations (6) for
n=1, but with the
An coefficients from (10).

Powered by TeXWeb (Win32, v.2.0).


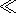 1 ) to which the
voltage
V is applied. According to the commonly accepted statement
[Wait, 1966],
the tangential component of the electric field of the slot
antenna
Eh,
different from zero at the gap, is determined by the
constant value independent of
h
1 ) to which the
voltage
V is applied. According to the commonly accepted statement
[Wait, 1966],
the tangential component of the electric field of the slot
antenna
Eh,
different from zero at the gap, is determined by the
constant value independent of
h 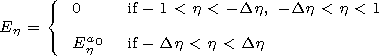
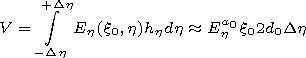
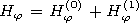
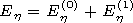
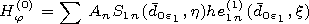

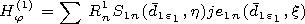
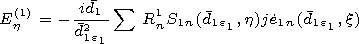
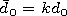 and
and 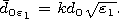
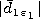 and
and 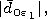 we obtain the
solution of the unrelated equation system in the form of the following
relation for the coefficients of expansions (8) and (9)
we obtain the
solution of the unrelated equation system in the form of the following
relation for the coefficients of expansions (8) and (9)
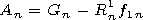
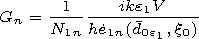

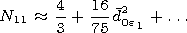
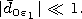 The harmonics with
n>1 in (8) have the amplitudes
An of the smaller
order
O(|d0e1n+1|) as compared to
n=1 and will not be taken into
account below.
The harmonics with
n>1 in (8) have the amplitudes
An of the smaller
order
O(|d0e1n+1|) as compared to
n=1 and will not be taken into
account below.
