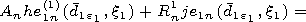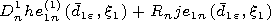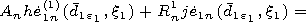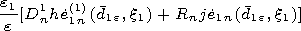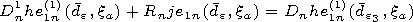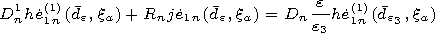2. Formulation of the Problem for the Dipole Antenna
|
|
Figure 1
|
[4] We consider first an equivalent problem for a prolate plasma spheroid
with the large and small semiaxes
a and
b and the eccentricity
e located in the medium with the relative dielectric permeability
e3. In the
center of the spheroid an electrical dipole oriented along the rotation
axis of the spheroid is located (Figure 1). We assume that the relative
dielectric permeability of the cold isotropic plasma is
at the chosen time dependence of the form
exp(- i wt),
where
wp is
the circular plasma frequency of electrons and
n is the effective collision
frequency.
[5] We assume that the depleted ion coating formed around the transmitter
has a form of a spheroid with the semiaxes
a1 and
b1 and with the
same eccentricity
e. The spheroid is filled in by the medium with the
relative dielectric permeability
e1.
The distance between the focal points
of the inner and outer spheroids will be designated
2d1 and
2d,
respectively. Below we will take the electrical dimensions of the
spheroids to be small, i.e.,
ka 1 and
k(|e|)1/2a
1 and
k(|e|)1/2a  1, where
k is
the wave number in the vacuum.
1, where
k is
the wave number in the vacuum.
[6] We will create the solution of the Maxwell equations in the outer
medium
e3 (Im
e3>0 )
satisfying the principle of radiation at the
infinity using the system of spheroidal functions
[Morse and Feshbah, 1953]
determined in the prolate spheroidal coordinate system
x, h, j (1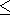 x<
x<  ,
-1
,
-1 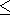 h
h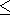 1 ) related to the outer spheroid
1 ) related to the outer spheroid
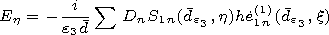 | (1) |
Here and below the values of the magnetic and electric fields are
multiplied by the impedance of the free space 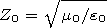 and by
and by  respectively. The following designations are used in (1):
respectively. The following designations are used in (1): 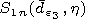 is the angular spheroidal function of the first kind and
is the angular spheroidal function of the first kind and  is the function related to the radial spheroidal functions of
the first kind
is the function related to the radial spheroidal functions of
the first kind 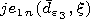 and second kind
and second kind  by the
formulae
here
by the
formulae
here 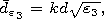 and
and 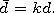 In the region of the depleted ion layer
e1,
we will create the solution
using the system of functions determined in the coordinate system related
to the inner spheroid:
In the region of the depleted ion layer
e1,
we will create the solution
using the system of functions determined in the coordinate system related
to the inner spheroid:
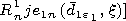 | (2) |
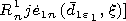 | (3) |
here 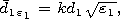 and
and 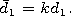
[7] In the region of the plasma layer with the relative dielectric permeability
e,
we will create the solution using two systems of functions
determined in the coordinate systems related to both inner and outer
spheroids:
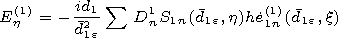 | (4) |
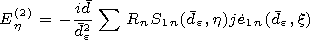 | (5) |
here 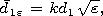 and
and 
[8] The following designations are used in expressions (1)-(5):
An are the
multipliers of excitation of the field of the electric dipole in the unlimited
space with the relative dielectric permeability
e1,
Rn1 and
Dn1 are the
reflection and transmission coefficients, respectively, for the boundary
between the inner medium and the plasma coating, and
Rn and
Dn are
the reflection and transmission coefficients, respectively, for the
boundary between the plasma coating and the outer medium.
[9] The excitation coefficients
An of the electromagnetic field of the source
located in the center of the spheroid have the form
where
x0 is the radial coordinate of the source,
I is the current at the
transmitter entrance, and
l is its effective length not exceeding the
length of the rotation axis of the inner spheroid and satisfying the
condition 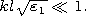 According to
Morse and Feshbah [1953],
in
the quasi-static approximation
According to
Morse and Feshbah [1953],
in
the quasi-static approximation 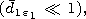 one can choose among
An the main coefficients corresponding to the index
n =1. Therefore
one can limit expansions (2)-(3) by one spheroidal wave with
n =1.
one can choose among
An the main coefficients corresponding to the index
n =1. Therefore
one can limit expansions (2)-(3) by one spheroidal wave with
n =1.
[10] Writing the boundary conditions of continuity of the tangential
components of the field on the surface of both spheroids and using for
the spheroidal functions the theorem of addition
[Ivanov, 1968]
(which
makes it possible to reexpand the solution of one system of functions in
terms of another system of functions related to the outer spheroid and
also to expand the angular spheroidal functions in the plasma medium on
the angular functions of the inner or outer medium
we obtain an infinite system of algebraic equations. In the quasi-statistics
condition, one can limit the angular function expansion with the accuracy
of the terms of the order of 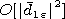 and
and 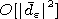 by the main
first term of the expansion with the coefficient
by the main
first term of the expansion with the coefficient  Similar error is obtained using the first term in the expansion in the
theorem of addition.
Similar error is obtained using the first term in the expansion in the
theorem of addition.
[11] Then confining ourselves by the main terms of the expansions we obtain
the boundary conditions on the inner
x=x1 and outer
x=xa surfaces
of the plasma spheroidal layer in the form of a truncated system of four
algebraic equations
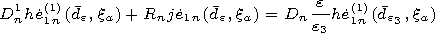 | (6) |
for
n=1.
From equation system (6), we find the coefficient
D1 of the
electromagnetic field propagation into the outer medium. Before finding
expression for
D1, we will formulate the second equivalent problem in
which a slot spheroidal antenna is used as an emitter.

Powered by TeXWeb (Win32, v.2.0).


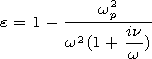
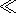 1 and
k(|e|)1/2a
1 and
k(|e|)1/2a 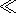 1, where
k is
the wave number in the vacuum.
1, where
k is
the wave number in the vacuum.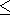 x<
x< 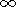 ,
-1
,
-1 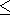 h
h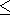 1 ) related to the outer spheroid
1 ) related to the outer spheroid
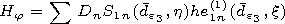
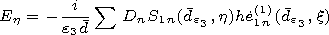
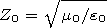 and by
and by  respectively. The following designations are used in (1):
respectively. The following designations are used in (1): 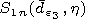 is the angular spheroidal function of the first kind and
is the angular spheroidal function of the first kind and  is the function related to the radial spheroidal functions of
the first kind
is the function related to the radial spheroidal functions of
the first kind 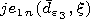 and second kind
and second kind  by the
formulae
by the
formulae
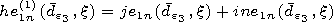
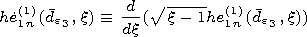
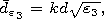 and
and 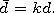 In the region of the depleted ion layer
e1,
we will create the solution
using the system of functions determined in the coordinate system related
to the inner spheroid:
In the region of the depleted ion layer
e1,
we will create the solution
using the system of functions determined in the coordinate system related
to the inner spheroid:
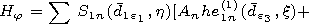
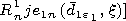
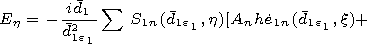
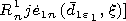
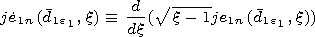
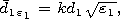 and
and 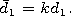
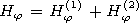
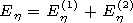
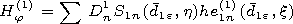
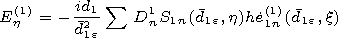
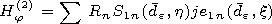
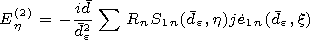
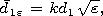 and
and 
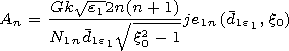
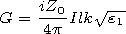

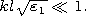 According to
Morse and Feshbah [1953],
in
the quasi-static approximation
According to
Morse and Feshbah [1953],
in
the quasi-static approximation 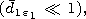 one can choose among
An the main coefficients corresponding to the index
n =1. Therefore
one can limit expansions (2)-(3) by one spheroidal wave with
n =1.
one can choose among
An the main coefficients corresponding to the index
n =1. Therefore
one can limit expansions (2)-(3) by one spheroidal wave with
n =1.
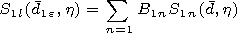
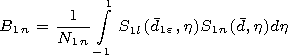
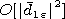 and
and 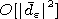 by the main
first term of the expansion with the coefficient
by the main
first term of the expansion with the coefficient  Similar error is obtained using the first term in the expansion in the
theorem of addition.
Similar error is obtained using the first term in the expansion in the
theorem of addition.