Discussion
[3] We consider the influence of the vegetation cover within a model
of homogeneous isotropic "forest layer" with effective values of
the electrical conductivity and dielectric permeability. In the case
when the wavelength
l of the electromagnetic wave is much
longer than the tree height
h ( l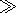 h ),
the influence of the latter
on electromagnetic wave propagation may be neglected
[Reinolds, 1953]
in the model of vertical electrical antenna with a capacitive
load. In this model the soil and tree branches form plates of a
condenser, whereas the tree trunk is equivalent to a resistance put
between the plates. In this case, at the impact on the tree of the
vertical component of the monochromatic field
En1 (the
dependence on time is accepted in the form
e-iwt ), in the
equivalent circuit of the tree with the effective height
hg, trunk
resistance
Rg, and capacity
Cg under the condition
khg
h ),
the influence of the latter
on electromagnetic wave propagation may be neglected
[Reinolds, 1953]
in the model of vertical electrical antenna with a capacitive
load. In this model the soil and tree branches form plates of a
condenser, whereas the tree trunk is equivalent to a resistance put
between the plates. In this case, at the impact on the tree of the
vertical component of the monochromatic field
En1 (the
dependence on time is accepted in the form
e-iwt ), in the
equivalent circuit of the tree with the effective height
hg, trunk
resistance
Rg, and capacity
Cg under the condition
khg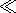 1 a
current
I (distributed almost homogeneously) appears:
1 a
current
I (distributed almost homogeneously) appears:
 | (1) |
where
Zg is the effective complex resistance of the tree,
k= w /c,
w is the circular frequency, and
c is the speed of light in the
vacuum.
[4] As a result of theoretical and experimental studies,
Egorov [1990]
showed that the predicted values of
Rg and
Cg may be calculated
with the accuracy of 10% using the formulae
 | (2) |
where
sg(t o C)
is the specific electrical conductivity of the wood
of the tree trunk depending on the temperature of the surrounding
medium,
S tr is the average area of the tree trunk,
S top is the area of
the lower part of its top, and
h top is the height of the lower part of
the top from the surface.
[5] If one neglects the finite conductivity of the soil and takes the tree
into account in the model of the vertical electrical antenna with the
capacity load, then, taking into account (1), the reemitted by the
tree vertical component of the electrical field on the ideally
conducting plane is determined as
 | (3) |
where
R= (r2g + hg2)1/2,
and
rg is the distance from the tree to the
observation point.
[6] We consider the case when trees are distributed with some density
n on the ideally conducting plane. Then the total field at the
observation point consists of the initial field
En1 that would have
existed in the absence of the trees and the total field of the trees
reemitting:
 | (4) |
Feinberg [1999]
showed that the field on the plane-underlying
surface with finite values of electrical properties of the lower
semispace may be presented in the form
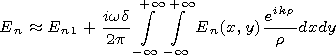 | (5) |
where
En1 is the field over the ideally conducting Earth surface,
and
d is the reduced surface impedance of the underlying surface.
[7] In the case of neglecting by the influence of static
( R-3 )
and
induction
( R-2 )
terms of the field reemitted by the trees (that is,
taking into account only the wave
( R-1 )
terms of this field) we
obtain, comparing (5) and (4)
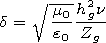 | (6) |
We estimate the ratio of the total field reemitted by all trees and
due only to the wave terms of the field to the quasi-static field
reemitted by one tree located in the close vicinity of the
observation point
(rg2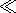 hg2 ).
hg2 ).
[8] The normal component of the electrical field in the case when the
emitter and the observation point are located on an impedance
plane has the form
[Feinberg, 1999]
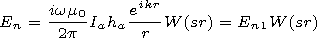 | (7) |
where
Ia and
ha are the current in the base of the emitting antenna
and its virtual height, respectively,
r is the distance from the
emission source to the measurement point,
W(sr) is the
attenuation function,
s= ikd2/2, and
d is the surface impedance
(6).
[9] Equalizing the right-hand sides of formulae (7) and (5), we obtain
the following expression for the total field reemitted by the trees
due only to the wave terms of the reemitted field
( R-1 ):
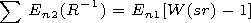 | (8) |
The normal component of the electrical field reemitted by one tree
in the direct vicinity of it may be found in the quasi-static
approximation
( R-3 )
from formula (3) under condition
rg2 hg2,
i.e.,
kR = khg
hg2,
i.e.,
kR = khg  1
1 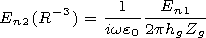 | (9) |
Taking into account the designation
we obtain from formulae (8) and (9) the sought for ratio of the total
field reemitted by all trees due only to the wave terms of the field
to the quasi-static field reemitted by one tree
Here
To estimate
|DEn| we use the results of experiments
[Egorov, 1990].
It follows from the latter that at a frequency of 250 kHz the
value
|e'f/(ef'-1)| = 2.3 at
rg 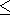 hg/4. Therefore, even in the most
unfavorable case
|sr|
hg/4. Therefore, even in the most
unfavorable case
|sr|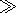 1, the secondary field reemitted by a tree
located at a distance equal to or smaller than
hg/4 (i.e., in the
direct vicinity of the observation point) is comparable by the
modulus to the total secondary field reemitted by all trees due to
only the wave terms.
1, the secondary field reemitted by a tree
located at a distance equal to or smaller than
hg/4 (i.e., in the
direct vicinity of the observation point) is comparable by the
modulus to the total secondary field reemitted by all trees due to
only the wave terms.
[10] In the quasi-static vicinity of the observation point within a large
forest, there are (depending on the wavelength) hundreds (MW),
thousands (LW), and even tens of thousands (ELW) of trees. So it
is evident that to estimate the secondary field reemitted by the
trees, one has in the first turn to take into account the influence of
the trees located in the quasi-static zone.
[11] According to the aforesaid we formulate the problem on
determination of the vegetation cover on propagation of
electromagnetic waves in the following way: on the ideally
conducting plane similar trees with the virtual height
hg and
effective complex resistance
Zg are distributed homogeneously.
One needs to determine in the quasi-static approximation the total
field reemitted by the trees. In this case, using formula (3), the total
quasi-static field reemitted by the trees may be written in the form
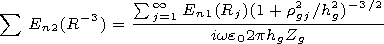 | (10) |
where
En1(Rj) is the normal component of the falling electrical
field from all the trees in the point of location of the
j th tree,
Rj is
the distance from the emitter to the
j th tree, and
rgj is the distance
from the
j th tree to the observation point.
[12] It follows from (3) that for all
k rgj 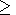 1,
i.e., for all the trees outside
the radius
rgj
1,
i.e., for all the trees outside
the radius
rgj 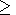 (l/2 p),
the input of the quasi-static terms of
reemission by the modulus is less than or equal to the input of the
wave terms of the reemission. In the previous considerations we
have already neglected the input of the wave terms of the field
reemitted by the trees. Therefore we may also neglect the influence
of the quasi-static terms of the reemitted field due to the trees
located outside the
l/2 p radius. Taking into account the
aforesaid, formula (10) may be transformed into the form of a
finite sum
(l/2 p),
the input of the quasi-static terms of
reemission by the modulus is less than or equal to the input of the
wave terms of the reemission. In the previous considerations we
have already neglected the input of the wave terms of the field
reemitted by the trees. Therefore we may also neglect the influence
of the quasi-static terms of the reemitted field due to the trees
located outside the
l/2 p radius. Taking into account the
aforesaid, formula (10) may be transformed into the form of a
finite sum
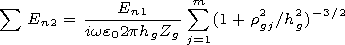 | (11) |
where
m is the number of trees located inside the circle with a
radius of
l/2 p.
Formula (11) takes into account that the falling
field
En1 within the
l/2 p circle stays almost constant.
[13] The total field reemitted by the trees (11) in principle may depend
on the location of the observation point within the large forest. We
estimate the total reemitted field in two extreme cases, that is,
when the observation point is located or directly near a particular
tree, or in the middle between four trees.
[14] Estimating the reemitted field in the direct vicinity of a tree, one
should take into account the influence of this tree determined by
formula (11) in the case of fulfilling the condition
rg/hg  0 ( m= 1).
In this case, 8 the nearest trees are located at sides and angles
of a rectangle with the side length of
2d ( d is the distance between
trees), that is, on the average located at a distance equal to the
semisum of radiuses of the circles inscribed into the rectangle and
described around it. The following 16 trees are located at sides and
in angles of a rectangle with the side length of
4d, etc.
0 ( m= 1).
In this case, 8 the nearest trees are located at sides and angles
of a rectangle with the side length of
2d ( d is the distance between
trees), that is, on the average located at a distance equal to the
semisum of radiuses of the circles inscribed into the rectangle and
described around it. The following 16 trees are located at sides and
in angles of a rectangle with the side length of
4d, etc.
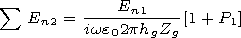 | (12) |
In the
m a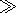 1 case,
1 case,
That is, series (12) is converging rapidly as a series for the
Riemann
x function
x(2). Taking into account that
we obtain
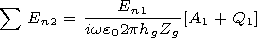 | (13) |
where
and
Q1 characterizing the estimate of an error of the series (13)
calculation.
[15] On the analogy to the previous example, the total field of
reemission in the point equidistant from the nearest four trees has
the form
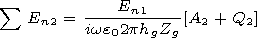 | (14) |
where
Q2 characterizes the estimate of calculation of series (14).
[16] Table 1 shows the results of calculation of the values of
A1 + Q1 and
A2 + Q2 as a function of the
a parameter characterizing the
thickness of large forests:
a = 1,
a = 0.5, and
a = 0.25 correspond
to thin, moderate, and thick forests. It follows from the table that
the total reemitted field under the given thickness of the forest
almost does not depend on the location of the observation point
between the trees, that is, it is a constant value in the quasi-static
vicinity
rg 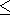 l /2 p relative to the observation point. Taking this
into account, it follows from (11) that the ratio of the normal
component of the falling electrical field
En1 to the normal
component of the total electrical field within the large forest
En1+
l /2 p relative to the observation point. Taking this
into account, it follows from (11) that the ratio of the normal
component of the falling electrical field
En1 to the normal
component of the total electrical field within the large forest
En1+ 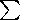 En2 is a constant value which according to the boundary
conditions for the normal components of the electric field at the
boundary between similar media characterizes the relative complex
dielectric permeability of the large forest
e'f in the model of a
homogeneous isotropic "forest layer"
En2 is a constant value which according to the boundary
conditions for the normal components of the electric field at the
boundary between similar media characterizes the relative complex
dielectric permeability of the large forest
e'f in the model of a
homogeneous isotropic "forest layer"
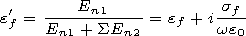 | (15) |
It follows from Table 1 that to calculate the total reemitted field
within the large forest, one can use the approximate formula
correct for any thickness of the forest within the interval:
The formula makes it possible to calculate the total reemitted field
with an error less than 5% by the modulus. Taking into account
formula (2) we have
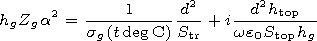 | (16) |
[17] In a large forest, the height of the top of all trees
h top is much
larger than that of a single staying tree and tends to the value of
hg , i.e.,
h top 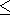 hg.
At the same time, the treetop in the forest
almost covers the entire area
d2 covered by this tree, i.e.,
d2
hg.
At the same time, the treetop in the forest
almost covers the entire area
d2 covered by this tree, i.e.,
d2 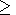 S top.
So one can take that the parameter
d2 h top/S top hg =1.
Substituting expression (16) into formula (15), we finally obtain
S top.
So one can take that the parameter
d2 h top/S top hg =1.
Substituting expression (16) into formula (15), we finally obtain
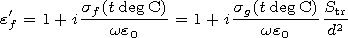 | (17) |
Similar consideration may be performed concerning the total
reemitted field of the tangential components of the magnetic field
of the trees. Because of the circular symmetry of the problem, the
tangential components of the magnetic field of the trees are
mutually compensated and the total reemitted magnetic field
within the large forest is absent.
[18] Thus in the case
l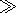 h, the influence of large forests on
propagation of electromagnetic waves (independently of the height
of the forest and its thickness) may be taken into account in the
model of homogeneous isotropic "forest layer" with the effective
dielectric and magnetic permeability equal to the dielectric and
magnetic permeability in vacuum, respectively. The effective
electric conductivity is determined by the formula
h, the influence of large forests on
propagation of electromagnetic waves (independently of the height
of the forest and its thickness) may be taken into account in the
model of homogeneous isotropic "forest layer" with the effective
dielectric and magnetic permeability equal to the dielectric and
magnetic permeability in vacuum, respectively. The effective
electric conductivity is determined by the formula
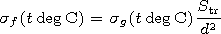 | (18) |
The dimensionless parameter
S tr/d2 characterizing the ratio of the
area covered by the tree trunks to the entire area of the large forest
may be determined using topographic maps of the scale
1:100,000 and larger, where the mean diameters of tree trunks and distances
between them are indicated.
|
|
Figure 1
|
[19] Figure 1 shows the values of the specific electric conductivity of
trunks of deciduous (solid curve 1) and coniferous (solid curve 2)
species of trees under direct current as a function of the
temperature (for central Europe) according to
Kashprovsky and Kuzubov [1971].
The values of
sg (t o C)
for deciduous and
coniferous trees coincide with each other in the temperature
interval from
+20 oC to
-5
o C and vary from
1.1 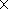 10-2 to
10-3 S m-1.
For other temperatures the curves diverge strongly. Figure 1 shows also the values of
sg (t o C)
for the coniferous species of
trees for the southern part of western Siberia (dashed curve)
[Zakharenko, 1991].
10-2 to
10-3 S m-1.
For other temperatures the curves diverge strongly. Figure 1 shows also the values of
sg (t o C)
for the coniferous species of
trees for the southern part of western Siberia (dashed curve)
[Zakharenko, 1991].
[20] One can see from Figure 1 that the specific electric conductivity of
trunks
sg (t o C)
of deciduous species of trees in central Europe
almost repeats the specific electric conductivity of trunks of
coniferous species of trees in the southern part of western Siberia
within the entire range of the environmental temperatures from
- 20 oC to
+20 oC
with the a standard deviation by a factor of 2.7.
[21] In principle, one can use the above presented values of
sg (t o C)
at
direct current in the hypothesis of the absence of frequency
dispersion. However, still stay unclear both the representativeness
of the
sg (t o C)
values at particular trees for different large forests
covering 40% of the Earth's land and the reliability of the
hypothesis of frequency dispersion absence.
[22] To solve the above indicated problems, we developed a method of
measurements of effective electric properties of a "forest layer"
directly at the frequencies of the emitted electromagnetic field.
[23] It is known that at falling of a plain vertically polarized wave
within a "forest layer" having the effective complex dielectric
permeability
e'f and located on the Earth's surface with the
relative complex dielectric permeability
e'g,
the following relation
is true:
 | (19) |
where
Hta is the tangential component of the falling magnetic
field at the air-forest boundary in the air,
En a is the normal
component of the falling electric field at the air-forest boundary in
the air,
Htf is the tangential component of the magnetic field
within the "forest layer" at any height
h 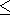 z
z 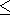 0, and
En f is the
normal component of the falling electric field within the "forest
layer" at any height
h
0, and
En f is the
normal component of the falling electric field within the "forest
layer" at any height
h 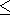 z
z 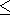 0.
Formula (19) is correct for any
falling angles of a plain vertically polarized wave.
0.
Formula (19) is correct for any
falling angles of a plain vertically polarized wave.
[24] The electromagnetic field from the vertical electrical antenna may
be presented as a superposition of plain waves, so one can state
that formula (19) is correct for the fields of radio stations at such
distances from the source that one can neglect induction-statistical
terms of emission and direct penetration of electromagnetic waves
through the "forest layer" and underlying Earth's surface, that is,
by all mechanisms of underground propagation in the soil and
within the large forest.
[25] As a result, we obtain that to determine
e'f,
it is enough to measure
the admittances of the electromagnetic field from radio stations
within the "forest layer" and in the air over the forest. Because of
technical difficulties of measuring admittance over the forest, in
the first approximation one can determine
e'f using measurements
of the admittance at some distance from the forest in the field and
in the forest along the front of the electromagnetic wave from the
radio station at distances
r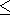 l, where
l is the wavelength of the
emitted wave.
l, where
l is the wavelength of the
emitted wave.
[26] We determined admittance using a two-channel selective
microvoltmeter, which makes it possible to measure the ratio of
amplitudes and phase shift of two signals in the MW range
channels. A rotating magnetic antenna was connected to one of the
channel for tuning to the maximum of the magnetic field. A
vertical electric antenna was connected to the other channel. The
measurements were conducted in three stages. First, the measuring
device was installed in a field at a distance larger than
10 hg from
the forest edge and the measurements of the value of
ga =(hm/hel)(Hta/Ena) were carried out. Then the measuring device was installed in the
forest at a distance larger than
10 hg from the forest edge and the
value of
gf =(hm/he1)(Htf/Enf) was measured. After than the device was
returned to the field at the same point in order to be sure that the
amplitude-phase characteristics of the device channels did not
change during the experiment. The ratio of
gf to
ga makes it
possible to exclude unknown values of the virtual heights of the
electric
hel and magnetic
hm antennae, i.e., to determine the soaked
for value of the effective complex dielectric permeability of the
"forest layer"
e'f.

|
|
Figure 2
|
[27] On the basis of numerous measurements of admittances at
frequencies of 250 kHz and 550 kHz in the summer, fall, and
winter conditions in the neighborhood of St. Petersburg in
coniferous (pine) and deciduous (birch) forests, we found that the
effective dielectric permeability of the "forest layer"
ef = 1.20 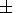 0.05 independently of the tree species and the
temperature of the environment within the entire range from
- 20 oC
to
+20 oC. The effective electric conductivity of the "forest layer"
sf (t o C)
also does not depend on the tree species and varies from
2.5
0.05 independently of the tree species and the
temperature of the environment within the entire range from
- 20 oC
to
+20 oC. The effective electric conductivity of the "forest layer"
sf (t o C)
also does not depend on the tree species and varies from
2.5 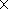 10-5 S m-1 (+20 oC) to
1.8
10-5 S m-1 (+20 oC) to
1.8 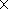 10-7 S m-1 (-20 oC).
The character
of the
sf (t oC)
behavior as a function of the air temperature is
shown in Figure 2 [Egorov, 2003].
10-7 S m-1 (-20 oC).
The character
of the
sf (t oC)
behavior as a function of the air temperature is
shown in Figure 2 [Egorov, 2003].
[28] Thus we succeeded in obtaining the effective values of the
complex dielectric permeability of the "forest layer" as a function
of the environmental temperature directly at the electromagnetic
field frequencies without any knowledge on the specific electric
conductivity of tree trunks
sg (t o C)
and on the values of the
dimensionless parameter
S tr/d2. It should be noted that the values of
the effective dielectric permeability of the "forest layer" are
obtained for rather local areas of large forests with the length of a
few tens of meters from the forest edge.
[29] In order to estimate the representativeness of the obtained data for
vast large forests in the Leningrad Region, we conducted
measurements of the modulus
|W| and additional phase
j add of the
attenuation function at a frequency of 350 kHz along a forest path
100 km long. The results of the measurements are shown in the
bottom line of Table 2
[Egorov, 2000].
[30] The propagation path may be characterized as a two-layer
structure. The large forest with a height of 15 m and effective
electric properties
(ef = 1.2,
sf = 2.5 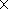 10-5 S m-1 in summer
( +15 oC) and
ef = 1.2,
sf = 2.5
10-5 S m-1 in summer
( +15 oC) and
ef = 1.2,
sf = 2.5 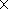 10-6 S m-1 in winter ( -5 o C),
Figure 2)
is located on the Earth's
surface which within the skin effect is
presented by well-studied soils and quaternary sediments and is
characterized by the values
eg = 20,
sg = 2.5
10-6 S m-1 in winter ( -5 o C),
Figure 2)
is located on the Earth's
surface which within the skin effect is
presented by well-studied soils and quaternary sediments and is
characterized by the values
eg = 20,
sg = 2.5 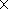 10-2 S m
-1.
The top
line of Table 2 shows the calculated values of the modulus and
phase of the surface impedance of the two-layer structure and
predicted values of the attenuation function.
10-2 S m
-1.
The top
line of Table 2 shows the calculated values of the modulus and
phase of the surface impedance of the two-layer structure and
predicted values of the attenuation function.
[31] It follows from Table 2 that the predicted and experimentally
measured values of
|W| differ by 10% and values of
j add differ by
0.1 rad, both values being within the accuracy limits of the model
and experiment.

|
|
Figure 3
|
[32] Points in Figure 3 show the experimental values of the attenuation
function
|W| as a function of the environmental temperature for the
frequency of 272 kHz along the path about 200 km long
[Korzhinskaya et al., 1991].
[33] The propagation path may be presented in the form of a two-layer
structure: the large forest with a height of 15 m with the effective
electric properties determined by Figure 2 is located on the Earth's
surface which within the skin effect layer is characterized by the
values
eg = 20,
sg = 1.4 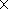 10-2 S m
-1.
The predicted values of the
modulus of the attenuation function
|W| for the above indicated
two-layer structure are shown in Figure 3 by the solid curve.
10-2 S m
-1.
The predicted values of the
modulus of the attenuation function
|W| for the above indicated
two-layer structure are shown in Figure 3 by the solid curve.
[34] A good agreement of the experiment and theory within the entire
range of environmental temperature variations from
-20 o C to
+20 o C makes it possible to state that local measurements of the
effective electric properties of the "forest layer" conducted in the
neighborhood of St. Petersburg are representative for large forest
with different area and composition located within the Freznel
zones (important for electromagnetic wave propagation) both in
the northwest part of the European part of Russia and in the
southern part of western Siberia.
[35] In conclusion, we consider one more feature of electromagnetic
wave propagation along forest paths. At electromagnetic wave
propagation along forest paths we, evidently, have the case, when
the modulus of the effective complex dielectric permeability of the
"forest layer" is much less than the modulus of the dielectric
permeability of the Earth's underlying surface
(|e'f| 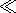 |e'g| ).
Therefore large forests may be physically presented as a thin badly
conducting layer located on the well-conducting base. This leads to
a decrease of the argument of the impedance of the two-layer path
as compared to the impedance of the base, i.e., to a shift into
strongly inductive region
(arg
dl < -p /4).
Makarov et al. [1991]
showed that, as a result, the modulus of the attenuation function at
some distances from the emitter becomes higher than unity. That
means that because of the influence of the Zennek surface wave,
the field over forest paths at some distances will be higher by the
modulus than the field over an infinite conducting plane.
|e'g| ).
Therefore large forests may be physically presented as a thin badly
conducting layer located on the well-conducting base. This leads to
a decrease of the argument of the impedance of the two-layer path
as compared to the impedance of the base, i.e., to a shift into
strongly inductive region
(arg
dl < -p /4).
Makarov et al. [1991]
showed that, as a result, the modulus of the attenuation function at
some distances from the emitter becomes higher than unity. That
means that because of the influence of the Zennek surface wave,
the field over forest paths at some distances will be higher by the
modulus than the field over an infinite conducting plane.

|
|
Figure 4
|
[36] Figure 4 shows results of the calculations of
dl for various
heights of forest as a function of the frequency for summer
conditions. It follows from Figure 4 that for all frequencies
f < 600 kHz,
arg
dl < -p /4 (a strongly inductive surface), whereas in the
frequency range
600-1000 kHz,
arg
dl > -p /4 (a weakly
inductive surface).

|
|
Figure 5
|
[37] Figure 5 shows the results of calculations of the attenuation
function modulus
|W| for the large forests with a height of 12.5 m
(solid curves) and of experimental measurements of
|W| (circles)
at the same path in summer at the air temperature of
+15 o C
[Egorov, 2002].
It follows from Figure 5 that (in a complete
agreement with the developed theory) at the frequency
f = 236 kHz,
because of the influence of the Zennek surface wave, the
attenuation function modulus
|W| >1 at distances up to 100 km
from the emitter, whereas at
f = 800 kHz, because of the shift of
the argument of the surface impedance
arg
dl into weakly
inductive region, the effect disappears.

Powered by TeXWeb (Win32, v.2.0).
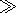 h ),
the influence of the latter
on electromagnetic wave propagation may be neglected
[Reinolds, 1953]
in the model of vertical electrical antenna with a capacitive
load. In this model the soil and tree branches form plates of a
condenser, whereas the tree trunk is equivalent to a resistance put
between the plates. In this case, at the impact on the tree of the
vertical component of the monochromatic field
En1 (the
dependence on time is accepted in the form
e-iwt ), in the
equivalent circuit of the tree with the effective height
hg, trunk
resistance
Rg, and capacity
Cg under the condition
khg
h ),
the influence of the latter
on electromagnetic wave propagation may be neglected
[Reinolds, 1953]
in the model of vertical electrical antenna with a capacitive
load. In this model the soil and tree branches form plates of a
condenser, whereas the tree trunk is equivalent to a resistance put
between the plates. In this case, at the impact on the tree of the
vertical component of the monochromatic field
En1 (the
dependence on time is accepted in the form
e-iwt ), in the
equivalent circuit of the tree with the effective height
hg, trunk
resistance
Rg, and capacity
Cg under the condition
khg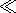 1 a
current
I (distributed almost homogeneously) appears:
1 a
current
I (distributed almost homogeneously) appears:
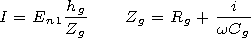

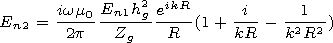
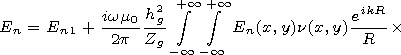

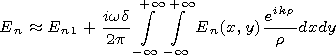
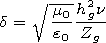
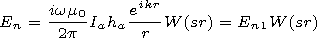
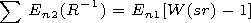
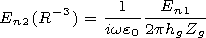
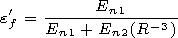

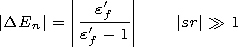
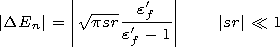
 hg/4. Therefore, even in the most
unfavorable case
|sr|
hg/4. Therefore, even in the most
unfavorable case
|sr|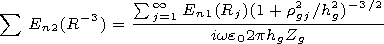
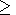 1,
i.e., for all the trees outside
the radius
rgj
1,
i.e., for all the trees outside
the radius
rgj 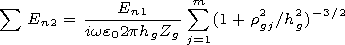
 0 ( m= 1).
In this case, 8 the nearest trees are located at sides and angles
of a rectangle with the side length of
2d ( d is the distance between
trees), that is, on the average located at a distance equal to the
semisum of radiuses of the circles inscribed into the rectangle and
described around it. The following 16 trees are located at sides and
in angles of a rectangle with the side length of
4d, etc.
0 ( m= 1).
In this case, 8 the nearest trees are located at sides and angles
of a rectangle with the side length of
2d ( d is the distance between
trees), that is, on the average located at a distance equal to the
semisum of radiuses of the circles inscribed into the rectangle and
described around it. The following 16 trees are located at sides and
in angles of a rectangle with the side length of
4d, etc.
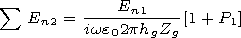
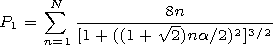
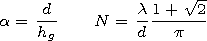
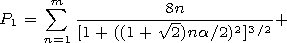
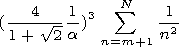
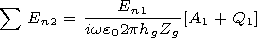
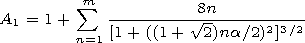
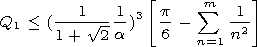
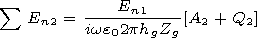

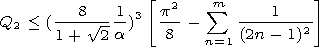
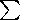 En2 is a constant value which according to the boundary
conditions for the normal components of the electric field at the
boundary between similar media characterizes the relative complex
dielectric permeability of the large forest
e'f in the model of a
homogeneous isotropic "forest layer"
En2 is a constant value which according to the boundary
conditions for the normal components of the electric field at the
boundary between similar media characterizes the relative complex
dielectric permeability of the large forest
e'f in the model of a
homogeneous isotropic "forest layer"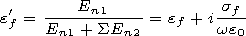

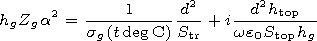
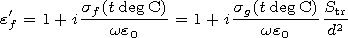
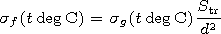

 10-2 to
10-3 S m-1.
For other temperatures the curves diverge strongly. Figure 1 shows also the values of
sg (t o C)
for the coniferous species of
trees for the southern part of western Siberia (dashed curve)
[Zakharenko, 1991].
10-2 to
10-3 S m-1.
For other temperatures the curves diverge strongly. Figure 1 shows also the values of
sg (t o C)
for the coniferous species of
trees for the southern part of western Siberia (dashed curve)
[Zakharenko, 1991].


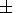 0.05 independently of the tree species and the
temperature of the environment within the entire range from
- 20 oC
to
+20 oC. The effective electric conductivity of the "forest layer"
sf (t o C)
also does not depend on the tree species and varies from
2.5
0.05 independently of the tree species and the
temperature of the environment within the entire range from
- 20 oC
to
+20 oC. The effective electric conductivity of the "forest layer"
sf (t o C)
also does not depend on the tree species and varies from
2.5 


