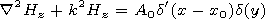
[7] It is easy to see that the Maxwell equations are reduced to the Helmholtz equations for Hz of the following form:
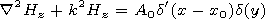 |
 Hz/
Hz/ n|G,
where
G is the outline of
the region and
n is a normal to it.
n|G,
where
G is the outline of
the region and
n is a normal to it.
[8] The point ( 0,h ) is a singular point of the Helmholtz operator. In order to get rid of the singularity we perform a conform transformation of coordinates transforming the lower and upper walls of the waveguide into planes. It is easy to see that the transformation w = (t2+h2)1/2 (where t=x+iy are the physical coordinates, w=x + i h are the conform coordinates, and the branch of the root is taken in such a way that Im(t2+h2)1/2>0 ) satisfies this requirement.
[9] It follows from the condition
x0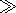 d that
x0
d that
x0 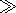 d. So we
find
d. So we
find
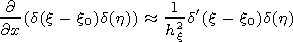 |
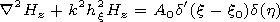 | (1) |
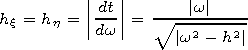 |
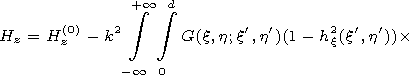 |
 | (2) |
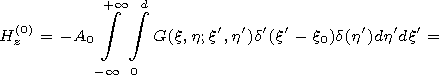 |
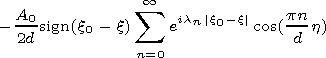 | (3) |
 1 if
|x|
1 if
|x|
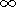 ,
the limitation of the integral operator in
L2 is provided.
[10] We will solve equation (2) by the sequential approximations
method. For its application one has to be sure that the norm of the
integral operator is less than unity:
,
the limitation of the integral operator in
L2 is provided.
[10] We will solve equation (2) by the sequential approximations
method. For its application one has to be sure that the norm of the
integral operator is less than unity:
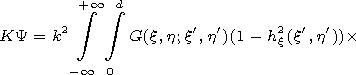 |
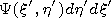 |
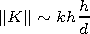 |
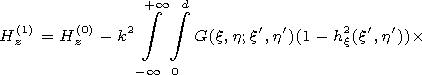 |
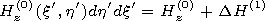 |
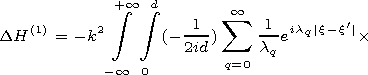 |
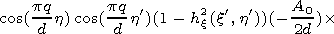 |
 |
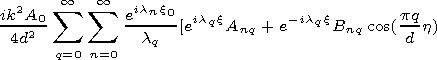 |
[11] Since all waves (except the zero one) are local waves,
x0 d,
and
|x|
d,
and
|x| d,
the only significant input into the field is
provided by the
A00 and
B00 coefficients. Therefore the further
solution is reduced to finding these coefficients.
d,
the only significant input into the field is
provided by the
A00 and
B00 coefficients. Therefore the further
solution is reduced to finding these coefficients.
[12] Neglecting by the terms of infinitesimal of higher orders of the kh(h/d) parameters we obtain
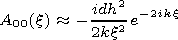 |
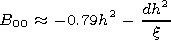 |
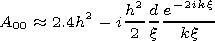 |
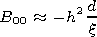 |
[13] Since all local waves are exponentially small (because
x0 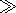 d and
|x| > d ), one can write an expression for the field taking into
account only the zero modes. Taking into account that the norm
K has
an order of
kh(h/d), one has in the first approximation to exclude all
the terms of the higher infinitesimal degree. This leads to a fact that in
the first approximation one can obtain a correction to the zero
approximation only in phase.
d and
|x| > d ), one can write an expression for the field taking into
account only the zero modes. Taking into account that the norm
K has
an order of
kh(h/d), one has in the first approximation to exclude all
the terms of the higher infinitesimal degree. This leads to a fact that in
the first approximation one can obtain a correction to the zero
approximation only in phase.
[14] To the left from the barrier (that is in the opposite relative to the source part of the waveguide) the expression for the field has the form
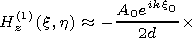 |
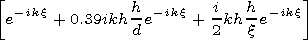 | (4) |
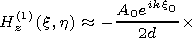 |
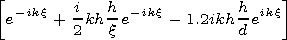 | (5) |
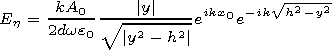 |
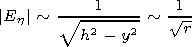 |
[15] Transferring (4) and (5) into physical coordinates and neglecting the terms of higher orders by kh(h/d) we obtain
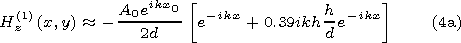 |
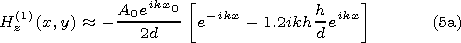 |
[16] Taking into account that
kh(h/d) 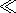 1 one can rewrite (4a) and
(5a) in the form
1 one can rewrite (4a) and
(5a) in the form
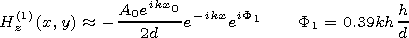 |
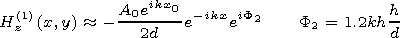 |
[17] Thus the obtained solution does not contain terms with the propagation and reflection coefficients depending on x. Both, the reflected and falling waves have constant amplitudes (at least with the accuracy to the second order of infinitesimal) also at |x|>d. Therefore the local irregularity (i. e., the barrier) provides the main influence on the propagation, but not the distributed one (curved upper wall).
|
| Figure 2 |
[19] TE case: \newline In the W1 region
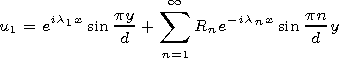 |
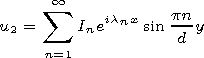 | (6) |
 |
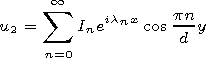 | (7) |
[20] According to the general scheme of MQGF, the Green function of the Laplace operator (satisfying the same boundary conditions as the solution) is used for the regularization of the system (6) or (7). Multiplying the fields and their derivatives by the normal derivative of the Green function and by the function itself, respectively, we integrate the fields over the boundary between regions. It can be easily shown [Konorov and Makarov, 1987] that such procedure is equivalent to a conversion of the Laplace operator.
[21] The functional equations obtained by the joining are expanded in a series about some complete system of functions and lead to a system of linear algebraic equations. According to the general MQGF theory [Konorov and Makarov, 1987; Verbitsky, 1981] the system is a regular one allowing for a truncation. Its matrix elements are double integrals of the Green function and functions used in the expansion.
[22] To find the Green function, we use a conformal transformation of coordinates
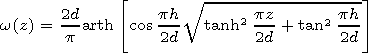 |
 |
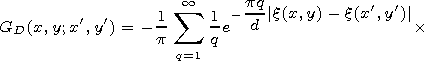 |
 |
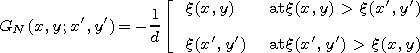 |
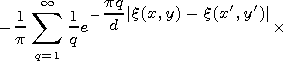 |
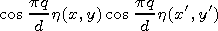 |
We consider first the Dirichlet's problem. Following the general scheme we obtain the functional equation
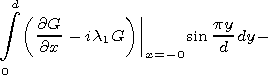 |
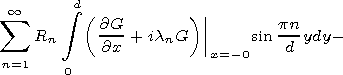 |
 | (8) |
Applying the second Green formula to the Green function and function in the and regions we find
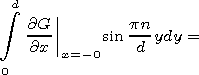 |
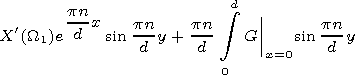 |
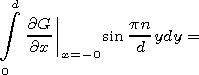 |
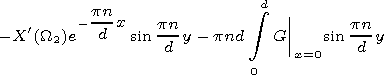 | (9) |
where
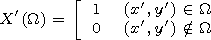 |
Using (9), we get rid of the derivative of the Green function in (8):
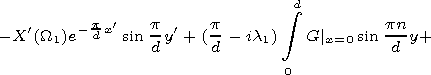 |
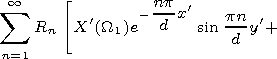 |
 |
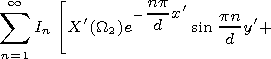 |
 | (10) |
Equation (10) at different x' is separated into two equations:
[23] In the
W1 region
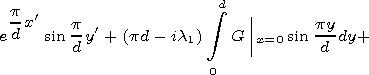
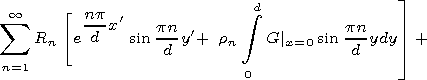 |
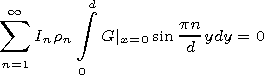 | (11) |
In the W2 region
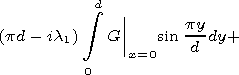 |
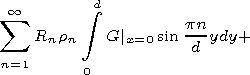 |
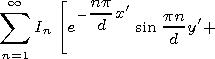 |
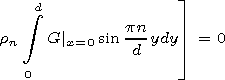 | (12) |
where the denotation rn=(pn/d) + i ln is introduced.
[24] Expressions (11) and (12) are functional equations. To move to linear algebraic system, one has to expand these equations in some complete system of functions. It is convenient to use { sin (pp/d)y'} as such functions. Multiplying (11) and (12) by sin (pp/d)y' and integrating with respect to y' between 0 and d we obtain
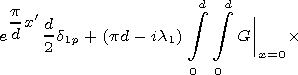 |
 |
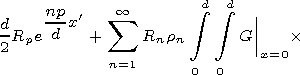 |
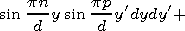 |
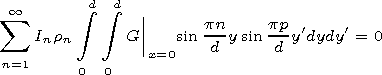 | (13) |
and
 |
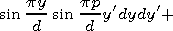 |
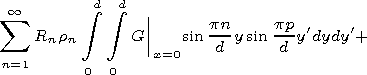 |
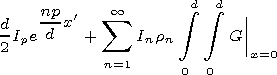 |
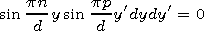 | (14) |
Taking into account that (13) and (14) should be fulfilled at any x', we take x'=0 and obtain the final system of equations
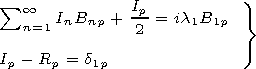 | (15) |
in which
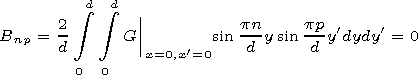 | (16) |
In a similar way we derive the system of equations in the case of the
Neumann problem. Its principal difference from the Dirichlet's
problem is that the Green function does not tend to zero at the infinity.
So the system of functions
{ cos (pp/d)y'}p 0 is not complete and one
should add to it
[1; x']:
projecting to these functions would give
"zero" equations:
0 is not complete and one
should add to it
[1; x']:
projecting to these functions would give
"zero" equations:
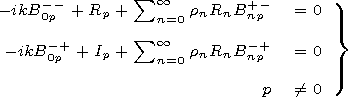 |
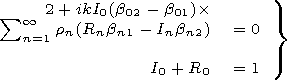 | (17) |
where
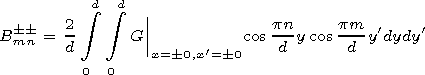 |
Thus regular systems of equations for the Dirichlet's and Neumann problems are obtained. Equations (15) and (17) allow for a reduction and (finding matrix elements) one can easily obtain the solution with the required accuracy, that is, in the numerical sense the problem may be considered as solved. However, if one is interested in analytical form of the solutions, one should study the Bmn dependency on the number of the element and waveguide parameters.
[25] In analytical solving the MQGF problems the main difficulty is determination of the matrix elements of the equation system, the elements being double integrals of the Green functions (16). To obtain the analytical dependence of the matrix elements on the problem parameters, we use the method suggested by Konorov and Makarov [1987].
[26] To do this, one has to obtain the expression of the matrix integrals in terms of the expansion coefficients of a conformal transformation by exponents. By rather inconvenient transformations one can obtain an expression for Bmn in the form of finite sums, the complexity of these sums growing quickly with an increase of the matrix element number.
[27] We will not describe in details the calculation of the matrix elements but present the first approximations (solutions of the first equation of the system only) for the Dirichlet's ( I1(1) ) and Neumann ( I0(1) ) problems:
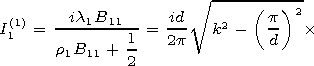 |
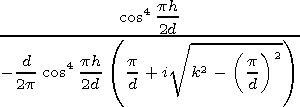 |
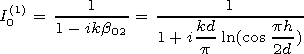 | (18) |
It is worth noting that unlike the first method considered there are no limitations to the barrier height h in this solution.
[28] Analytical expressions for the second and third approximations are also obtained; however, they are rather massive. Comparing the solutions of systems containing one, two, and three equations, one can study the correction introduced into the solution by every new equation and evaluate the accuracy of the final result.

|
| Figure 3 |
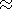 d/2, to have more exact determination of
I1 one should take
the system of two equations. The third equation introduces the
correction not exceeding 10%. Figure 3 shows the behavior of the
modulus of the propagation coefficient of the first mode as a function
of the barrier height for
d=10 and
k=0.5.
d/2, to have more exact determination of
I1 one should take
the system of two equations. The third equation introduces the
correction not exceeding 10%. Figure 3 shows the behavior of the
modulus of the propagation coefficient of the first mode as a function
of the barrier height for
d=10 and
k=0.5.

|
| Figure 4 |
[31] Now we consider solution of the Neumann problem under
small height of the barrier. In this case, expression (18) for the
coefficient at the zero wave may be approximately written in the
following form:

(19)
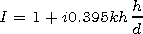 | (20) |
One can see that solutions (19) and (20) are almost the same. Therefore the curved upper wall gives almost no input into wave propagation. Thus one can conclude that, solving problems of propagation in the Earth-ionosphere waveguide, the main influence on the field is provided by local irregularities of the Earth surface (especially at the presence of angular points), but not smooth perturbations in the ionosphere.

Powered by TeXWeb (Win32, v.2.0).