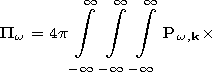
[21] We will consider (as it has been done above) a source having only the electric dipole moment p'= p'0 e'z exp (-iw'0 t') in the "proper" reference system (PRS) and moving with a constant velocity v= v ez relative to the "laboratory" reference system (LRS). Unlike in sections 2 and 3, we will now assume that the medium moves with a velocity u= u ez relative to LRS. For the sake of definiteness, we take u>0, whereas the sign of v may be arbitrary. In this section we consider the case of the medium with the refraction index n= (em)1/2>1 which may be considered almost constant within a wide frequency range.
[22] The procedure of determination of the field in this problem may be different. On one hand, one is able to solve directly equations for this or that potential (for example, for the Hertz vector) in the moving medium using the Fourier method and taking into account the causality principle or the Mandelstam radiation condition. On the other hand, one can use the known spatial-time Green function [Bolotovskiy and Stolyarov, 1983]. Certainly, all the ways give the same final result. Below we describe the former way.
[23] From the equations for electromagnetic field in a moving medium [Bolotovskiy and Stolyarov, 1983], there follows the following expression for the Fourier image of the Hertz vector:
|
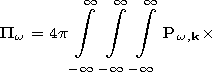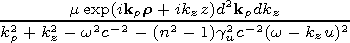 | (11) |
)
to the integral along the entire real axis
( - ).
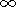
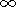The
latter integral will contain the Hankel function
H0(1)(kr r),
and the
integrating contour going along the upper shore of its cut. Determining the
rule of the going round the poles of the integrand on the
kr plane, one
should use the Mandelstam radiation principle requiring the group velocity
of the propagating waves
vg to be directed from the
z axis
[Bolotovskiy and Stolyarov, 1972].
Using the known properties of the group velocity
of waves in a moving medium
[Bolotovskiy and Stolyarov, 1976],
one
can easily find which of the poles on the
kr plane should be gone round
from below (the condition
vg r>0 should be fulfilled for it) and which one
should be gone round from above. After determination of the positions of
the poles, the integral over
kr is found by closing the contour into the
upper semiplane. The integral over
kz is taken easily due to the fact that
the Fourier image
Pw, k contains a delta function. As a result, we have
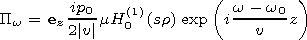 | (12) |
The value s squared standing in the argument of the Hankel function is
 |
 |
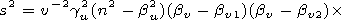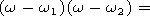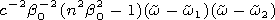 | (13) |
where
 |
 |
 |
 |
 |
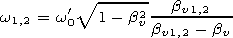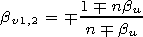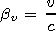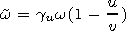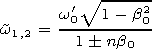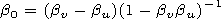 | (14) |
Here the variable w has the sense of the frequency in the rest system of the medium, and b0 represents the dipole motion velocity in this system.
[24] We see that the s value may be either real, or imaginary. In the latter case, its imaginary part is positive (s=i|s|) and that provides exponential decrease of the generated "inhomogeneous waves". In the s2>0 case, the physically correct sign of s is obtained as a result of the application of the Mandelstam radiation principle as it has been mentioned above. It is determined by the following rules:
[25] 1. If bv1<bv<bv2 (i.e., n2 b02<1 ), the value s is real only in the limited region of frequencies w min<w<w max, where w min= min{w1, w2}, and w max= max{w1, w2}. In this case s>0.
[26] 2. If bv<bv1 or bv>bv2 (i.e., n2 b02>1 ), the value of s is real in two semilimited regions: at w<w min and w>w max. In this case,
 |
It is worth emphasizing that the inequalities bv1<bv<bv2 are equivalent to the requirement n2 b02<1 which means that the dipole moves relative the medium with the velocity lower than the phase speed of light in the medium. Therefore the given case may be called a regime of "subluminal relative motion" (SubRM). The inequalities bv<bv1 or bv>bv2 are equivalent to the requirement n2 b02>1 and therefore this case may be called a regime of "superluminal relative motion" (SupRM). As in the case of a motionless medium, in the SubRM regime, the range of the emitted frequencies (i.e., the region of the real values of s ) is finite, whereas in the SupRM regime it is infinite.
[27] Components of the electromagnetic field in the moving medium are expressed via the Hertz vector according to the known formulae [Bolotovskiy and Stolyarov, 1983] (we would not write them down here). The calculation of the spent to radiation source power averaged over the period we perform using the Pointing vector integration over the surface surrounding the source. If one, as usually, takes as such a surface an infinite cylinder surface the axis of which coincides with the source motion trajectory, one obtains the following expression for the averaged power
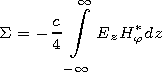 | (15) |
One can transform this integral identically to a more simple form using methods used in the classical theory of radiation of moving sources in the motionless medium [Frank, 1981]. Omitting all intermediate calculations, we present here the final result of this procedure:
 |
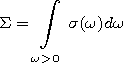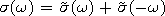 | (16) |
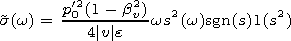 | (17) |
The presence of the unit Heaviside function 1(s2) shows that (as in a motionless medium) the integration is performed only over the part of the frequency axis where the value s(w) is real (which is quite natural because only in this frequency range there are propagating waves).
[28] It is worth noting that integral (16) is convergent only in the case of a limited radiation spectrum, that is, at bv1<bv<bv2. If the spectrum is unlimited, integral (16) is divergent in the case of the medium without dispersion. Here we have an analog of the energetic "paradox" known in the Vavilov-Cerenkov radiation theory [Bolotovskiy, 1957; Frank, 1981; Ginzburg, 1987, 2002; Zrelov, 1968]: the source moving with a superluminal velocity in a motionless nondispersive medium should loose infinite energy in a unit of time. In our case such situation arises in the SupRM motion, i.e., at either bv<bv1 or bv>bv2. It is known that this paradox may be resolved, for example, at taking into account the frequency dispersion of the medium which inevitably leads to limitations of the radiation spectrum.
[29] Calculating integral (15) in the n2 b02<1 case, we obtain
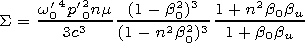 | (18) |
In particular cases of motionless medium and motionless source, expression (18) is reduced to the known results: at bu=0 we have [Ginzburg and Frank, 1947b]
 |
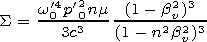and at bv=0 we have [Daly et al., 1965; Doil'nitsyna and Tyukhtin, 2003, 2004]
 |
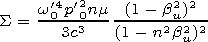The most interesting feature of expression (18) is the fact that it changes sign at some parameters of the problem. Under the condition n2b0 bu>-1 which is equivalent to inequality
 |
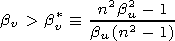the radiation power is positive, whereas under the condition n2b0 bu<-1 (i.e., at bv<bv* ) it becomes negative. The latter means that if the source lags considerably behind the medium stream, it obtains energy from the energy of the moving medium. It should be noted that in the considered SubRM regime such effect is possible only for the "superluminal" flow of the medium when nbu>1 (because only in this case the inequality bv1<bv*< bv2 is fulfilled). For its realization, the velocity of the source motion should be considerably less than the medium motion velocity, because bv*<bu ). Certainly, this effect will take place also in the SupRM regime; however, in this case the radiation power in the model of nondispersive medium appears to be infinite (as it has been already noted, this "paradox" may be resolved by taking into account the dispersion).
[30] The effect of the sign reversal of the energy wave losses was noted earlier for the case of a charge moving in the moving medium [see, e.g., Bolotovskiy and Stolyarov, 1983]. However, in this case the radiation field presents only in the SupRM regime and, respectively, only in such regime the effect of the sign reversal of energy wave losses is possible. To be exact, the effect is realized under the condition bv< bv1, whereas for the oscillator this effect takes place under the condition bv< bv*. Since bv*> bv1, it is evident that this phenomenon for an oscillator occurs at smaller difference in velocities bu- bv than for a charge.
Powered by TeXWeb (Win32, v.2.0).