Energetic characteristics of radiation of oscillating...

3. Case of Resonant Medium

[11] Now we consider such case when an electric dipole is moving in the nonmagnetic and nonabsorbing medium having the dispersion of a resonant type. We have for the medium with one resonant frequency:

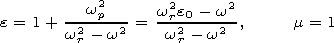
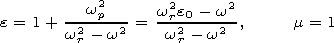(7)

where w_r and w_p are the resonant and plasma frequencies, respectively, and e₀= 1+w_p²/w_r² is the permittivity of the medium relative to the static field. It is worth noting that for such medium, a detailed study of the radiation even in the simplest case of a moving point charge was performed only in the recent years. In particular, Afanasiev and Kartavenko [1998] and Afanasiev et al. [1999] analyzed the radiation of a charge in an infinite resonantly dispersive dielectric, and Tyukhtin [2004b] considered the radiation in a waveguide filled in by a dielectric.

[12] Substituting (7) into (2), we obtain

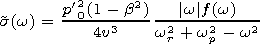(8)

where

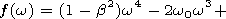(9)

Condition (3) determining the range of the emitted frequencies is reduced to the following requirements:

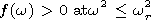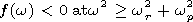(10)

(in the frequency region w_r² <w² < w_r² + w_p², there can be no radiation at all, because condition (3) is not fulfilled due to negative value of e ).

[13] One can obtain relatively simple formulae for the boundary frequencies and radiation energies at some limitations on the problem parameters. We present below only the estimates for boundary frequencies. We assume first that the resonant frequency of the medium is much less than the oscillator frequency in the laboratory frame of reference: w_r 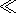w₀ =w₀'(1-b²)^1/2. Then it is easy to show that there exist two frequency ranges in the radiation spectrum. 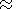The first one is determined by the inequalities w_*<w<w_r, where w_* approx w_r(1+ b²w_p²w₀^-2)^-1/2. This frequency range may be called a "resonant" one because it is located in the vicinity of the resonance frequency w_r. 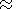The second emitted frequency range is determined by the inequality w₁<w<w₂, where w_1,2 approx (w₀' 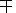b(w₀'²- w_p²)^1/2)/(1-b²)^1/2. This range may be called a "proper" one because at relatively small velocities it includes the oscillator frequency w₀' (however, it should be borne in mind that at sufficiently high values of b, the lower boundary of this range becomes higher than w₀' ). We emphasize that this frequency range in the radiation spectrum exists only under condition w₀'>w_p. It is worth also noting that the "resonant" and "proper" frequency ranges at the condition w_r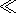 w, as a rule, are located rather far from each other. One can show that the "resonant" radiation is much weaker than the "proper" radiation (if the latter does exist). We emphasize that in the case w₀ < w_p, the "proper" radiation disappears, whereas the "resonant" radiation takes place at any relation between the plasma frequency and proper frequency of the source.

[14] If w_r w₀, two principally different possibilities may be realized. The first one takes place at b(e₀^1/2<1 when the dipole motion velocity v is less than the phase velocity of the low-frequency radiation (c/(e₀)^1/2 ). In this case there exist both the "proper" range of the emitted frequencies and the "resonant" range adjacent to the frequency w_r. 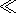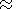For the "resonant" radiation under the additional condition w₀(1-b²)^1/2 w_r(1-b²e₀)^1/2, we obtain the frequency range w_*<w<w_r, where w_* approx w_r ((1-b²e₀)/(1-b²))^1/2. 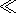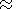For the "proper" radiation under the additional condition w₀ w_r(1-b(e₀)^1/2), we obtain the frequency range w₁<w<w₂, where w_1,2 approx w₀/(1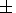b (e₀)^1/2). It is worth noting that in these conditions both the "resonant" and "proper" radiations may prevail.

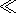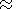[15] In the case when w₀ w_r but b(e₀)^1/2>1, the radiation spectrum contains only one frequency range w_*<w<w_r, where w_* approx w₀/(1+b (e₀)^1/2). One can show that in this situation, the total radiation power depends very weakly on the oscillator frequency.

Figure 3

[16] Figures 3a, 3b, 3c, and 3d show the spectral density of the radiation energy as a function of the dimensionless frequency W = w/w'₀ at various values of the dimensionless resonant ( W_r = w_r/w'₀ ) and plasma ( W_p = w_p/w'₀ ) frequencies and the source motion velocity. Figure 3a shows a typical picture for the situation when both the resonant and plasma frequencies are less than the oscillator frequency: w_r<w'₀ and w_p <w'₀. In this case, there are two frequency ranges: the "proper" radiation is dominating and the "resonant" one is insignificant. Figure 3b illustrates the case when w_r<w'₀ and w_p >w'₀. In this case there is only one ("resonant") range of radiation frequencies.

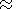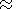[17] Figure 3c is typical for the case when w_r>w'₀ and w_p <w'₀. In this case three possibilities may be realized. If the dipole motion velocity is less than some value b_* ( b_* approx 0.433 for the values of the parameters used in Figure 3c), there are both the "resonant" and "proper" (relatively low-frequency) ranges. If b_*< b< b_** (in our case b_** approx 0.82 ), there is only one frequency range including the oscillator frequency and adjacent to the resonant frequency. If the oscillator velocity is high enough ( b> b_** ), then (besides this range) there is one more range lying above the resonance frequency. Figure 3d illustrates the case when w_r >w'₀. and w_p >w'₀. In this case two possibilities can be realized: either there are two frequency ranges (if the velocity is low enough), or there is only one range.

Figure 4

[18] Figures 4a and 4b show the dependence of the total power of the dipole radiation on the velocity of its motion at various resonant and plasma frequencies. Figure 4a corresponds to the case when the resonant frequency is lower than the oscillator frequency ( W_r<1 ). If the plasma frequency is also lower than the oscillator frequency ( W_p<1 ), there are both the "proper" and "resonant" radiations, the former one prevailing. In this situation, the dependence of the radiation power on the velocity is insignificant. If W_p>1, only relatively weak "resonant" radiation is generated. It has fairly well pronounced dependence on the velocity with a maximum at some of its value. Figure 4b corresponds to the case when the resonant frequency exceeds the oscillator frequency. In this case the dependence of the power on the velocity has a maximum, its value increasing with an increase of the plasma frequency.

[19] Concluding this section, we emphasize that the comparison of the obtained results with the results for the cases of nondispersive medium and cold plasma shows that the presence of the resonant dispersion leads to different, much more complicated, regularities characterizing the radiation of a moving oscillator.