6. Discussion

Figure 6

[18]  One can see from Figure 6 that the average values of T_n (i.e., T_n ) in the Southern Hemisphere increase with an increase in latitude from 40^o to 65^o by ~180 K, whereas the product [O]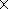 [N₂] almost does not change, because [N₂] increases with latitude and [O] decreases proportionally. In spite of the increase in T_n, the balance altitude h_m0 decreases with latitude by 26 km (see Table 1) as a result of the transition from the nighttime conditions to the daytime conditions. The height h_mF2 decreases by 18 km, this fact demonstrates that the contribution of the vertical drift into h_mF2 increases by 8 km. In the Northern Hemisphere, h_mF2 decreases by 26 km at the transition from middle to high latitudes, h_m0 decreases by 32 km and therefore the contribution of the wind into h_mF2 increases by 6 km (see Table 1).

[19]  The value aW 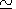V cos D sin 2I, so the average velocity of the meridional wind V increases strongly at approaching high latitudes to compensate the decrease in the average value of the product cos D sin 2I (by factors of 2.4 and 1.9 in the Northern and Southern hemispheres, respectively) and to provide the increase in W. That is what is actually observed in Figures 4c and 5c.

[20]  The longitudinal variations in the temperature of the thermosphere T_n follow by shape the variations of the geographic latitude j at a fixed invariant latitude, they are small in amplitude and insignificantly increase with an increase in latitude (from 0.06 T_n to 0.14T_n ) (Figure 6). Almost the same is true for the longitudinal variations in the product [O]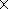 [N₂] what determines the contribution of the thermospheric composition into variations in h_mF2 and also slightly increases with an increase in latitude (from 35% to 38% relative to the mean value of [O]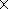 [N₂]. Therefore the increase in the LE amplitude in h_m0 (from ~22 km at 40^o to ~31 km at 65^o) is not determined by these factors, but is related mainly to the variations in the illumination conditions both with latitude and longitude. In the Northern Hemisphere the difference between the geomagnetic and geographic poles is less, so these variations are also less and the amplitude of LE in h_m0 changes slightly (from 13 to 16 km). At such values of the LE amplitude in h_m0, its contribution into the longitudinal variations in h_mF2 in the Northern Hemisphere is about 25% and almost does not change with latitude, whereas in the Southern Hemisphere this contribution increases with latitude from 30% to 40%. Thus the changes in the average value of h_mF2 with latitude are mainly provided by variations in the balance height, whereas the longitudinal variations in h_mF2 are caused for the most part by the drift.

[21]  Now we consider changes with latitude in the contribution of the both wind components into the longitudinal variations in h_mF2. According to (2) the contribution of the meridional wind component may be presented as a V+ aV + aV a V aV , where V is the zonally averaged value of V, V is its variations with longitude, and similar designations are introduced for the value a = 0.5 cos D sin 2I. The product a V provides the most significant contribution into the longitudinal variations in h_mF2. However, in the Northern Hemisphere it decreases sharply toward high latitudes since the mean value of cos D sin 2I decreases in amplitude by a factor of 2.4 and the amplitude of LE in the meridional wind component increases insignificantly. The weakening of the effect of V in the Northern Hemisphere is partly compensated by the effect of V, because both multipliers of the product aV, increase toward high latitudes. The wind in the Southern Hemisphere behaves in such a way that the contributions of V and V almost do not change with latitude.

[22]  The neutral wind is generated by the solar heating of the thermosphere and is governed by the ion drag. Since N_i sin D, one may assume that the longitudinal variations in the meridional wind in the geomagnetic coordinate system are determined as some combination cj + d sin D, where j is geographic latitude. The analysis shows that one can adjust the c and d coefficients in such a way that the dependencies similar to those in Figure 4c would be obtained. However, those are only quantitative considerations. Determination of the causes of LE in the neutral wind velocity needs a special analysis. The longitudinal variations in the meridional wind in the Southern Hemisphere calculated on the basis of h_mF2 data differ rather strongly by shape from the variations in the HWM model; however, in the longitudinal variations of all parameters in Figure 5, a local maximum at longitudes of 150- 210^o is clearly pronounced. Thus a regional peculiarity in the wind system in the Southern Hemisphere takes place and needs explanation.

[23]  Similarly, the contribution of the zonal component of the wind is determined by the expression b U+ b U+ b U b U+ b U where b = 0.5 sin D sin 2I. The longitudinal variations in the product sin D sin 2I slightly vary with latitude by both the shape and amplitude, therefore the changes of the contribution of the zonal component are determined mainly by its own changes. In both hemispheres with an increase in latitude, the direction of the zonal wind changes from the eastward to westward. As a result, the contribution of the zonal wind into drift variations is positive at middle latitudes but at high latitudes becomes negative and causes to a decrease of the LE amplitude (especially strong in the Southern Hemisphere). Thus, though the average values of the amplitude of the longitudinal variations in the neutral wind components increase at a transition from middle latitudes to high latitudes, the relative contribution of the wind into the longitudinal variations in h_mF2 slightly decreases. In the Northern Hemisphere it is mainly due to the decrease of the contribution of the longitudinal variations in the wind meridional component, whereas in the Southern Hemisphere it is related to the change in the zonal wind direction. This decrease in the contribution of the wind is compensated by the increase of the contribution of h_m0, so finally the LE amplitude in h_mF2 almost does not change with latitude.

[24]  The comparison of the variations in h_mF2 in the Northern and Southern hemispheres shows the presence of a strong asymmetry. The longitudinal variations in the height of the F2 -layer maximum are stronger by amplitude in the Southern Hemisphere and at the first approximation are described by one first harmonic, whereas in the Northern Hemisphere they are described by two harmonics comparable by magnitude. The obtained results make it possible to understand more clearly the causes of the asymmetry. At a fixed geomagnetic latitude, the variations in geographic latitude govern the longitudinal variations in the thermospheric composition. These variations are stronger in the Southern Hemisphere than in the Northern Hemisphere and differ by the sign, this determines the great difference in the h_m0 variations. The asymmetric action of the wind is mainly determined by the magnetic field declination D. The variations in sin D determine domination of the first harmonic in the Southern Hemisphere and the presence of two harmonics in the Northern Hemisphere. In the Northern Hemisphere, atmospheric parameters are often characterized by two harmonics too; this is evidence of an inverse influence of the ionosphere on the thermosphere, probably, via ion drag. Finally, a strong impact is provided by the longitudinal variations in the neutral wind velocity. However, the causes of the longitudinal variations in the both components of the wind are not known, so the problem of the asymmetry is not solved completely.

Powered by TeXWeb (Win32, v.2.0).