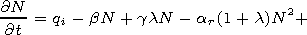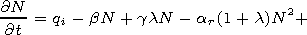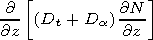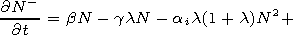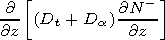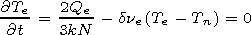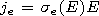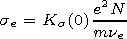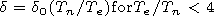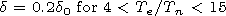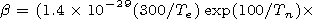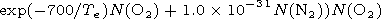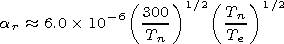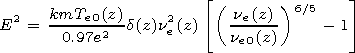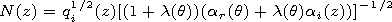2. Ionospheric D-Region Disturbances
Under Quiet Conditions
[4] In the absence of external tropospheric disturbances, i.e.,
under quiet conditions in a plane stratified medium, the basic
functional relations between the ionospheric parameters and the
parameters of large mesospheric electric fields are given by
[Martynenko, 1999a, 1999b;
Martynenko et al., 2001]
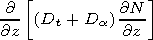 | (1) |
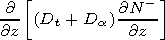 | (2) |
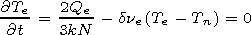 | (3) |
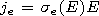 | (4) |
where
qi is the ion production rate,
b is the effective electron
attachment rate,
g is the effective electron detachment rate,
l =N-/N,
N is the electron number density,
N- is the negative ion
number density,
ar is the effective coefficient of electron-ion
recombination,
ai is the effective coefficient of ion-ion
recombination,
Dt is the coefficient of eddy diffusion,
Da is the
coefficient of ambipolar diffusion,
Qe/N is the mean energy
imparted to an electron by the mesospheric DC electric fields,
Tn is the neutral species temperature,
d is the fractional loss of
energy per electron collision with a molecule,
je is the density of
the current driven by a mesospheric current source,
se is the
electron conductivity of the ionospheric
D-region plasma, and
E is the intensity of the quasi-steady mesospheric electric field.
Here, equations (1) and (2) are the nonlinear continuity equations
for the electrons and negative ions, respectively, (3) is the
nonlinear energy equation for the electrons, and (4) is the
nonlinear Ohm's law for the large mesospheric electric field. In
writing equations (1)-(3), the weakly ionized, ionospheric plasma
is assumed to be quasi-neutral, and the positive and negative ion
temperatures to be equal to the neutral constituent temperature. In
the
D region,
Qe = jeE =seE2.
In addition, the following
dependences are taken into account
[e.g., Gurevich, 1978;
Tomko et al., 1980]:
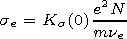 | (5) |
 | (6) |
,
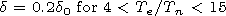 | (7) |
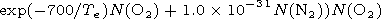 | (8) |
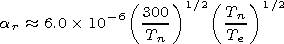 | (9) |
where
Ks(0) = 1.42 [Gurevich, 1978],
e is the electron charge,
m is the electron mass,
Nn is the number density of neutral particles,
N( O2 )
is the number density of molecular oxygen in cm-3,
N( N2) is the number density of molecular nitrogen in cm-3,
Te and
Tn are
in K,
va in s-1,
ar in cm3 s-1,
subscript "0" is used to denote the
magnitude of the plasma parameters in the absence of large
mesospheric electric fields.
[5] Martynenko [1999a, 1999b] and
Meek et al. [2004]
have
shown that the diffusion processes may be neglected in treating
the evolution of the disturbed ionospheric
D region parameters
over spatial scales of more than 150 m and temporal scales less
than a few tens of minutes. Then the relation between the
disturbing electric field intensity
E(z) and the disturbed
ne and
d values in the lower part of the
D region is given by
[Martynenko, 1999a, 1999b;
Martynenko et al., 2001]
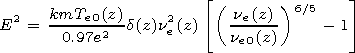 | (10) |
where
k is Boltzmann's constant and
Te0(z) and
ve0(z) are related
by (6). Relation (10) is a quasi-stationary solution to the set of
nonlinear equations (3)-(5) closed by the electron heat flow
(Joule heating) equation
Qe = seE2. It describes, along with the
collision term (6) and (7), the dependence
ne(E) implicitly. The
disturbed value of
N(z) is given by
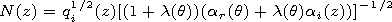 | (11) |
where
q= Te/Te0.
[6] Hence the set of theoretical relations (1)-(11) provides the
framework for modeling studies of how large mesospheric
electric fields affect the ionospheric
D -region parameters. The
disturbances in the electron temperature and effective collision
frequency (see equations (6) and (10)) are the primary cause of
disturbances in other parameters. Equation (4) relates large
mesospheric electric fields and the low-frequency conductivity of
electron plasma. Equation (6) provides the relationship between
disturbances in the electron temperature and the effective
collision frequency. Equation (7) establishes disturbances in the
fractional loss of energy per electron collision with a heavy
particle. Equation (8) is used to calculate the effective rate at
which the negative ions are formed by attachment of electrons to
neutral constituents. Equation (9) shows disturbances in the
effective rate of electron-ion recombination. Equation (11)
defines explicitly, the disturbances in the electron number density.
The quantity
q characterizes the degree to which the ionospheric
plasma departs from local thermodynamic equilibrium, with
q = 1 being for the ionosphere in local thermodynamic equilibrium in
the absence of large mesospheric electric fields. The relative
disturbance
h = ne/ n0 is related to
q by the relation
h = q5/6 (see
(6)). Estimates show that
q = 1.8 for the most probable value of
E= 0.57 V m-1 at midlatitudes
[Martynenko, 2002;
Meek et al., 2004],
with a disturbance of
N of a few percent (see (11)).
[7] Thus the electrically active mesosphere is the cause of the
observed violation of local thermodynamic equilibrium in the
lower part of the
D region,
z < 70 km, with the electron
temperature enhanced above the neutral temperature. The MF
radar observations of
Meek et al. [2004]
have revealed elevated
electron temperatures in approximately 70-75% of the cases
when the MF radar echoes occur from the 60-67 km altitude.

Powered by TeXWeb (Win32, v.2.0).