4. Envelope of a Chirped Pulse
[11] The second-order correction to the complex amplitude
F2 satisfies the inhomogeneous equation
and the boundary conditions
 F2/
F2/  r|r=0 =0 and
F2
r|r=0 =0 and
F2  0 at
r
0 at
r
 .
The condition of solvability of this problem implies the
equation for the pulse envelope
U(q,s)
.
The condition of solvability of this problem implies the
equation for the pulse envelope
U(q,s)
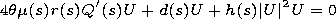 | (9) |
The coefficients of the equation are given by
The dependence of the coefficients of (9) on variable
s manifests the influence of the longitudinal irregularity of the
waveguide channel on evolution of the pulse envelope and, in
particular, on its linear frequency modulation.
[12] Solution of (9) in a general case can be performed by
the method described in the books by
Molotkov [2003]
and
Molotkov et al. [1999].
As a first step, it is necessary to solve
a simplified model problem, which will lead to the
conclusions on a qualitative behavior of the solution. Then
this solution can be used as a structural basis of the ansatz for
the solution of the complete problem.
[13] To simplify the problem (9), we impose additional
restrictions on the longitudinal inhomogeneity of the
waveguide. We write the sought function
U in the form
extracting explicitly an exponential multiplier with the
envelope phase and, similarly to
Bisyarin and Molotkov [2002],
the multiplier that characterizes amplitude variations
as functions of the longitudinal coordinate. Let us suppose
that the
u(q,s) function defined in such a way depends on the
variable
alone, which can be achieved if the coefficients of (9) are
related by
It is these relations that present additional assumptions on the
longitudinal irregularity of the waveguide. Under these
conditions the
u(x) function obeys the second Painlevé
equation
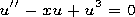 | (10) |
This equation is well studied from the point of view of
existence of moving critical points in the solutions
[see
Golubev, 1950;
Kudryashov, 2004,
and references therein];
a
relation with linear integral equations of definite kinds has
been investigated in detail by
Ablowitz et al. [1978, 1980].
Gibbon et al. [1985]
has proved that it is possible to construct
N -soliton solutions of nonlinear differential equations in
partial derivatives if they possess the Painlevé property.
Reduction of the second Painlevé equation to a linear integral
equation and the proof of the existence of bounded solutions
were given by Ablowitz and Segur [1977].
|
|
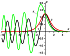
Figure 1
|
[14] In our work, the numerical solution of (10) was
performed by the Runge-Kutta method. Figure 1 shows the
graph of this solution (curve 1). For the sake of a comparison,
Figure 1 presents a sech soliton with the same amplitude
(curve 2) and the Airy function (curve 3). The soliton of the
nonlinear Schrödinger equation is the solution of a similar
problem
[Bisyarin and Molotkov, 2002]
without frequency
modulation. The Airy function is presented for comparison
because linearization of (10) is the Airy equation. The plotted
solution has a localized character, that is, it tends to zero at
|x|  0. Comparison with the sech soliton leads to the
conclusion that a linear frequency modulation of the high-
frequency carrier of the pulse gives rise to formation of an
oscillating tail of the envelope and leads to a greater
steepness of the leading edge of the pulse.
0. Comparison with the sech soliton leads to the
conclusion that a linear frequency modulation of the high-
frequency carrier of the pulse gives rise to formation of an
oscillating tail of the envelope and leads to a greater
steepness of the leading edge of the pulse.

Powered by TeXWeb (Win32, v.2.0).
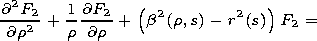
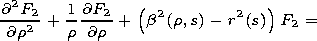
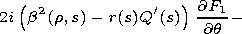

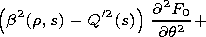
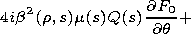
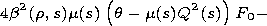
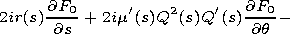
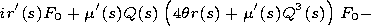
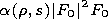
 F2/
F2/ 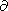 r|r=0 =0 and
F2
r|r=0 =0 and
F2  0 at
r
0 at
r
 .
The condition of solvability of this problem implies the
equation for the pulse envelope
U(q,s)
.
The condition of solvability of this problem implies the
equation for the pulse envelope
U(q,s) 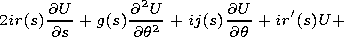
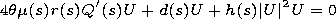
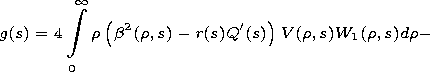
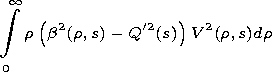

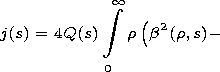
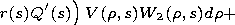
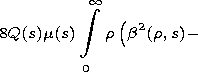

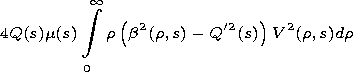
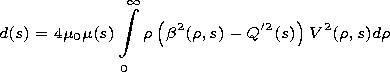
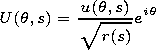
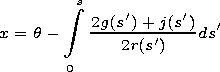
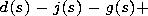
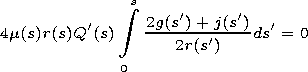
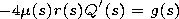
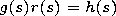
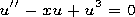

 0. Comparison with the sech soliton leads to the
conclusion that a linear frequency modulation of the high-
frequency carrier of the pulse gives rise to formation of an
oscillating tail of the envelope and leads to a greater
steepness of the leading edge of the pulse.
0. Comparison with the sech soliton leads to the
conclusion that a linear frequency modulation of the high-
frequency carrier of the pulse gives rise to formation of an
oscillating tail of the envelope and leads to a greater
steepness of the leading edge of the pulse.
