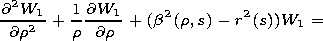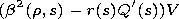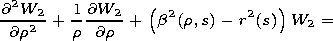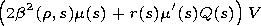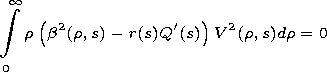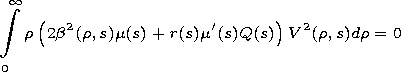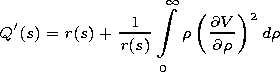3. Mode Structure and Pulse Modulation Function
[6] By substituting (3) and (4) into (2) and setting the terms
of the same order with respect to
d equal to zero, we get a set
of boundary problems for second-order differential equations
which, in combination with the conditions of solvability of
these problems, allow one to determine successively all the
elements of the ansatz.
[7] The
F0(r, q, s) function is the solution of the
Sturm-Liouville problem
 | (5) |
Bisyarin and Molotkov [2002]
have demonstrated the solvability of
this problem for a sufficiently wide and practically important
class of the
b(r,s) functions. Let
r2(s) be the eigenvalue of the
problem (5) and let
V(r,s) be the eigenfunction corresponding
to this eigenvalue and normalized by the condition
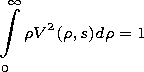 | (6) |
[8] The complex amplitude in the principal order can be
presented as a product
where
U(q,s) describes the envelope of the selected mode in
the main approximation. Below we shall refer to it as the
pulse envelope.
[9] The first-order correction in expansion (4) satisfies the
equation
and the same boundary conditions as function
F0. The
solution of this problem has the structure that makes it
possible to express the dependences on phase
q via functions
U and
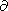 U/
U/ 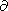 q
q
[10] Here the pair of functions
W1 and
W2 is defined as solutions
of inhomogeneous equations
that satisfy the boundary conditions in problem (5). If for the
right-hand sides of these equations the relations
are fulfilled, such functions
W1 and
W2 exist. This allows one,
with due account of the condition of normalization (6), to
express the envelope phase and modulation function through
the eigenvalue and the eigenfunction of the problem (5)
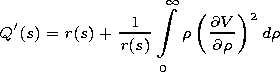 | (7) |
 | (8) |
Equations (7) and (8) establish the relation between the
modulation function and the
Q(s) and
R(s) functions that
determine phases of the envelope and high-frequency carrier
of the propagating mode. The modulation function is
therefore related to these functions and cannot be specified in
an arbitrary manner. It varies in accordance with (8) as the
pulse propagates in a longitudinally inhomogeneous
waveguide.

Powered by TeXWeb (Win32, v.2.0).


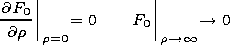
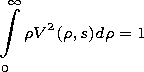
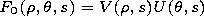
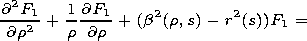
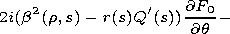
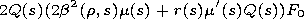
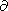 U/
U/ 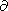 q
q