1. Introduction
[2] Propagation of pulses with a linear deviation of the
carrier frequency in dispersive media is accompanied by the
effects that make these pulses potentially promising for
solution of a number of practical problems. A linear
frequency modulation can prove to be a factor that partially
counteracts dispersion. For instance, in the linear propagation
regime a quadratic phase modulation gives rise to focusing of
a pulse in time, that is, up to some distance the pulse
compression occurs and only then its dispersion spreading
begins
[Akhmanov et al., 1988;
Vinogradova et al., 1990].
Phase modulation via a more complicated law can lead to
splitting of the initial pulse into two separate pulses
[Helczynski et al., 2002].
[3] Propagation of powerful probing pulses in the
ionosphere leads to excitation of nonlinear effects and
formation of waveguide channels
[Molotkov, 2003;
Molotkov et al., 1999].
Bisyarin and Molotkov [2002]
studied propagation of a
short electromagnetic pulse in a graded-index waveguide
with a weak longitudinal irregularity. The goal of the work
described here was to investigate the process of propagation
of a weakly nonlinear pulse using an additional assumption
that the carrier frequency depends linearly on time.
[4] The phase of a chirped pulse is expressed as
F = wt + mw2 t2,
where parameter
m characterizes the
modulation depth. The instantaneous frequency is
w + 2mw2t ,
and the total variation in the instantaneous
frequency of the pulse with duration
t is given by
The spectral width
DW of the pulse with duration
t is the
magnitude of the order of
t-1. Let us compare the modulation
depth and spectral width. To this end, we compose the ratio
between the total variation in the instantaneous frequency and
the spectral width of the pulse as
where
T is the oscillation period,
T= 2 p/w. In the problem
considered here it is assumed that the pulse contains a
sufficiently large number of carrier periods, and therefore the
ratio between the oscillation period and pulse duration is a
small parameter of the problem. By designating this ratio as
d, we get
 | (1) |
Relation (1) allows one to classify chirps according to their
depths. The pulses with
Dw/DW d, i.e.,
m
d, i.e.,
m d3, will be
called chirped pulses. It is these pulses that will be considered
in this paper. It is natural to refer to the pulses whose range of
instantaneous frequency variation is comparable with the
spectral width as strongly chirped pulses. Investigation of
their propagation is a separate problem which is beyond the
scope of this paper.
d3, will be
called chirped pulses. It is these pulses that will be considered
in this paper. It is natural to refer to the pulses whose range of
instantaneous frequency variation is comparable with the
spectral width as strongly chirped pulses. Investigation of
their propagation is a separate problem which is beyond the
scope of this paper.

Powered by TeXWeb (Win32, v.2.0).
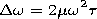
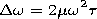


 d, i.e.,
m
d, i.e.,
m d3, will be
called chirped pulses. It is these pulses that will be considered
in this paper. It is natural to refer to the pulses whose range of
instantaneous frequency variation is comparable with the
spectral width as strongly chirped pulses. Investigation of
their propagation is a separate problem which is beyond the
scope of this paper.
d3, will be
called chirped pulses. It is these pulses that will be considered
in this paper. It is natural to refer to the pulses whose range of
instantaneous frequency variation is comparable with the
spectral width as strongly chirped pulses. Investigation of
their propagation is a separate problem which is beyond the
scope of this paper.
