4. Role of Gravitation

Figure 3

[17]  The calculations in which real plasma parameters in the solar corona were specified and the gravitational forces of the Sun were taken into account have shown that, because of a high 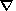P at the start of calculations, the effect of gravitation is nearly unnoticeable, and the distributions of plasma parameters at t<25 turn out to be similar to those in the absence of gravitation (Figure 3). As the corona expands, the velocity maximum moves away from the Sun. The highest velocity is 5.5 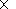10⁷ cm s ^-1. The maximum velocity of plasma flow is reached at the portion of the X axis where density and temperature gradients are not zero. However, as the corona expands and the gradients of the plasma density and temperature decrease, the force 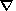P and gravitational force near the left boundary become comparable, and the flow velocity becomes lower than in the calculations assuming zero gravitation. A local decrease in velocity leads to a local plasma accumulation, i.e., to an increase in the density. As this takes place, the gradient near the left boundary 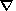(nkT)/nM_i again increases, and the plasma velocity directed away from the Sun restores its value. This again causes smoothing of the gradient, i.e., the flow is no longer stable. This leads to the conclusion that an additional acceleration is needed for the stable generation of the solar wind in the presence of gravitation. Such an additional acceleration mechanism could be MHD waves generated on the photosphere and absorbed in the corona [Chashey, 1997].

[18]  The nonstationarity of the flow in the vicinity of the Sun obtained in calculations allowing for gravitation can also be a result of an incorrect choice of the dimensionless parameter b₀ = 8 pn₀kT₀/B₀². It follows from the approximate Parker's formula that the solution is very sensitive to the integration constant, and the solar wind can be formed only under clearly defined conditions in the corona. By assuming that in the corona kT = 200 eV and n =2 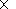10⁷ cm ^-3, we take into consideration only a pressure gradient of the electron gas. However, it can hardly be expected that the electron temperature of the corona considerably exceeds the ion temperature because the time during which the electron and proton temperatures become equal, estimated as t(c) 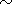2 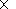10⁷ T_e^3/2/n, is not longer than an hour. Direct measurements of the electron temperature obtained from an ionization equilibrium and the ion temperature through Doppler broadening of spectral lines also point to T_e 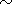200 eV and T_e 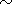T_i [Doschek and Feldman, 2000; Seely et al., 1997]. Here, T_e is the electron temperature in eV, and n is the number of electrons in cm ^-3. If the electron temperature T_e in the corona plasma is comparable to the ion temperature T_i, the dimensionless parameter of pressure force should be written as 8 pn₀k(T_e + T_i)/B₀². At T_e = T_i the dimensionless coefficient of pressure force in (3) should be taken to be 2 b₀ rather than b₀.

Figure 4

[19]  To understand whether, in principle, the stationary outflow of solar wind can exist due to additional acceleration, we performed the calculations in which the pressure force was increased by a factor of 2, i.e., the dimensionless coefficient of pressure force in equation (3) was taken to be 2 b₀. The results of calculations are depicted in Figure 4. Figure 4a shows distributions of plasma parameters along the X axis for t=11.29. The increases in plasma density and temperature occur here within the computational domain, and the velocity maximum has not yet reached the right boundary. 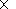The maximum velocity exceeds 5 10⁷ cm s^-1. It is reached at the portion of the X axis where the pressure gradient is not zero. The magnetic field lines are extended at this portion by the flow of expanding plasma (Figure 4b). However, in the region nearer to the right boundary, where the plasma flow has not yet arrived, the field lines differ only slightly from the dipole ones. The velocity maximum shifts beyond the computational domain to the moment of time t 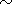40. Distributions of the plasma parameters and the field lines for t=127.29, when the stationary flow is about to be established, are shown in Figures 4c and 4d. No local minima in velocity obtained in calculations ignoring ion temperature gradient (Figure 3) are observed near the left boundary. In this case acceleration by the pressure gradient is more effective, and influence of gravitation is not considerable. The cross marks the point of transition of the plasma flow to the supersonic regime. The transition occurs smoothly at a distance of 2.8 R from the center of the Sun, while at neglecting ion pressure the distance of transition is 4.5 R. In both cases the magnetic field lines are extended in the entire computational domain, formation of the heliospheric current sheet in the computational domain takes place.

Figure 5

[20]  Formation of the current sheet leads to turn of the magnetic field vectors. An increase of the radial component of the magnetic field near the sheet and a decrease of the transverse component in the sheet occur (Figures 5a and 5b). Distributions of the radial component of the magnetic field, plasma flow velocity, plasma density and current density across the sheet at a distance of 8 solar radii are shown in Figures 5c and 5d. These dependences have the regularities similar to those clearly observed at crossings of the current sheet by spacecrafts at large heliocentric distances. The current sheet is located inside a thicker layer with an increased plasma concentration, the minimum of the solar wind velocity is inside the sheet [Borrini et al., 1981; Smith, 2001].

Figure 6

[21]  Comparison of the results of calculations involving the coefficients of pressure force of b₀ and 2 b₀ shows that taking into account the ion temperature gradient provides the stationary thermal expansion of the solar corona plasma in the presence of gravitation and formation of the heliospheric current sheet. If this is so, introduction of the coefficient less than unity before the term in the equation of motion will lead to a change in the direction of velocity in the calculations including typical parameters of the corona and accretion of material. Figure 6 shows results of calculations for the coefficient equal to (5/8) b₀. 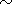Here, a local minimum of velocity arises near the left boundary already at t 20, but the velocity is still directed away from the Sun, and the magnetic field lines are extended in this region. Later, the minimum becomes even deeper, and the velocity reverses the direction. The plasma flow from the corona changes the direction, and the plasma accumulates near the left boundary, where the boundary conditions are taken to be a constant corona density and plasma velocity corresponding to the loss of the solar mass. Thus, for the stable solar wind generation to take place, ions in the corona must be heated to the temperature close to the electron temperature.

Powered by TeXWeb (Win32, v.2.0).