
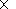 10-20 g cm-3 ),
temperature ( T0 = 20 eV), magnetic field
( B0 = 1 G), velocity
( V0 = B0/4 pr0
10-20 g cm-3 ),
temperature ( T0 = 20 eV), magnetic field
( B0 = 1 G), velocity
( V0 = B0/4 pr0 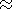 2
2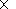 109 cm s-1 ),
length ( L0 = 8 R
109 cm s-1 ),
length ( L0 = 8 R 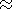 6
6 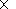 1011 cm), time
( t0 = L0/V0
1011 cm), time
( t0 = L0/V0 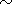 300 s), and current
density
( j0
300 s), and current
density
( j0 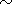 1.3
1.3 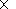 10-12 A cm
-2 )
were used. Here,
mi = 1.67
10-12 A cm
-2 )
were used. Here,
mi = 1.67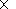 10-24 is the
mass of proton,
and
R= 6.9
10-24 is the
mass of proton,
and
R= 6.9 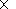 1010 cm
is the Sun's radius.
The system of three-dimensional MHD equations in the dimensionless
form is
1010 cm
is the Sun's radius.
The system of three-dimensional MHD equations in the dimensionless
form is
 | (1) |
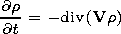 | (2) |
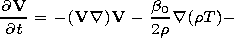 |
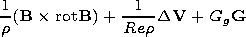 | (3) |
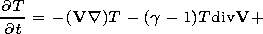 |
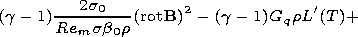 |
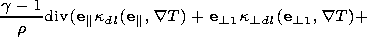 |
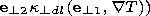 | (4) |
[8] In equations (1)-(4),
Rem = L0V0/nm0 is the magnetic Reynolds number,
nm0 = c2/4ps0 is the magnetic viscosity for conductivity
s at temperature
T0, and
s is the conductivity,
s0/s = T-3/2. The dimensionless coefficient
b0 = 8pn0 kT0/B02, where
n0 = r0/mi.
It should be
emphasized that
b0 in this form is not the ratio between plasma pressure
and pressure of magnetic field at a definite point in space, it is simply a
dimensionless coefficient expressed through the dimensionless units used
for the calculations. The term including viscosity does not exert a
considerable influence on the results; it is important for increasing the
stability of the finite difference scheme.
Re = r0 L0 V0/h is the Reynolds
number,
h is the viscosity,
Gq = L(T0) r0 t0/T0,
L(T dimens ) is the radiation
function for ionization equilibrium in the corona,
T dimens= T0T.
L'(T) = L(T dimens)/L(T0) is the dimensionless radiation function. In the problem
being solved, radiation did not have a strong effect;
e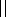 ,
e
,
e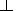 1,
e
1,
e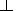 2 are the
orthogonal unit vectors parallel and perpendicular to the magnetic field;
kdl = k/(Pk0 )
is the dimensionless coefficient of thermal conductivity
along the magnetic field;
P = r0 L0 V0/k0 is the Peclet number;
k0 is the
thermal conductivity at temperature
T0;
k is the thermal conductivity;
k/k0 = T5/2;
k
2 are the
orthogonal unit vectors parallel and perpendicular to the magnetic field;
kdl = k/(Pk0 )
is the dimensionless coefficient of thermal conductivity
along the magnetic field;
P = r0 L0 V0/k0 is the Peclet number;
k0 is the
thermal conductivity at temperature
T0;
k is the thermal conductivity;
k/k0 = T5/2;
k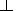 dl = [(kk0-1P-1) (kB k0B-1PB-1)]/ [(kk0-1P-1) +(kB k0B-1PB-1)] is
the dimensionless coefficient of thermal conductivity in the direction
perpendicular to the magnetic field;
PB = r0 L0 V0/k0B is the Peclet
number for the thermal conductivity across a strong magnetic field (when
the cyclotron radius is much smaller than the free path). Thermal
conductivity across a strong magnetic field is denoted as
kB; and
k0B is
its magnitude for temperature
T0, plasma density
r0 and magnetic field
B0;
kB/k0B = r2B-2 T-1/2.
Gg G is the dimensionless gravitational
acceleration.
Gg= t02/L0, G
is the gravitational acceleration, and
g is the
adiabatic constant.
dl = [(kk0-1P-1) (kB k0B-1PB-1)]/ [(kk0-1P-1) +(kB k0B-1PB-1)] is
the dimensionless coefficient of thermal conductivity in the direction
perpendicular to the magnetic field;
PB = r0 L0 V0/k0B is the Peclet
number for the thermal conductivity across a strong magnetic field (when
the cyclotron radius is much smaller than the free path). Thermal
conductivity across a strong magnetic field is denoted as
kB; and
k0B is
its magnitude for temperature
T0, plasma density
r0 and magnetic field
B0;
kB/k0B = r2B-2 T-1/2.
Gg G is the dimensionless gravitational
acceleration.
Gg= t02/L0, G
is the gravitational acceleration, and
g is the
adiabatic constant.
[9] The parameters used for calculations were:
g = 5/3,
Rem=8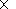 104,
Re=104,
b0=8
104,
Re=104,
b0=8 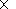 10-6,
P=2,
PB=2
10-6,
P=2,
PB=2 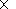 106. (We repeat here, that
b0 is not the ratio
between plasma pressure and magnetic pressure at a definite point in
space, it is only coefficient in equations (1)-(4), which is determined by
dimensionless units of pressure and magnetic field). In numerical and
laboratory simulation it is impossible to use very big and very little
dimensionless parameters. These parameters are chosen bigger or less
than unit, but not precisely by the same order of magnitude. The
principles according to which the dimensionless parameters were chosen
were described by
Podgorny and Podgorny [1995, 1996].
For the
numerical calculations, the grid
41
106. (We repeat here, that
b0 is not the ratio
between plasma pressure and magnetic pressure at a definite point in
space, it is only coefficient in equations (1)-(4), which is determined by
dimensionless units of pressure and magnetic field). In numerical and
laboratory simulation it is impossible to use very big and very little
dimensionless parameters. These parameters are chosen bigger or less
than unit, but not precisely by the same order of magnitude. The
principles according to which the dimensionless parameters were chosen
were described by
Podgorny and Podgorny [1995, 1996].
For the
numerical calculations, the grid
41  41
41  41 was used; therefore the magnetic
Reynolds number was ~50.
41 was used; therefore the magnetic
Reynolds number was ~50.
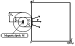
|
| Figure 1 |
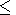 x
x 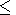 1,
0
1,
0 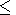 y
y 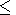 1,
0
1,
0 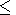 z
z 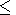 1.
The positions of the Sun, corona, and
computational domain in the
y = 0.5 plane are shown in Figure 1. The
dipole giving rise to the magnetic field
B0
1.
The positions of the Sun, corona, and
computational domain in the
y = 0.5 plane are shown in Figure 1. The
dipole giving rise to the magnetic field
B0 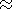 0.8 G on
the Sun's surface
is parallel to the
Z axis. The magnetic moment of the dipole in
dimensionless units is
M1={M1x=0,
M1y=0,
M1z=9.6
0.8 G on
the Sun's surface
is parallel to the
Z axis. The magnetic moment of the dipole in
dimensionless units is
M1={M1x=0,
M1y=0,
M1z=9.6 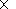 10-2}.
Its center is
at the point
R1 = {x1 = -0.217,
y1 = 0.5,
z1 = 0.5}.
On the face
x = 0,
at the point
y = 0.5 and
z = 0.5, the magnetic field is 0.15 G.
The lines of the
10-2}.
Its center is
at the point
R1 = {x1 = -0.217,
y1 = 0.5,
z1 = 0.5}.
On the face
x = 0,
at the point
y = 0.5 and
z = 0.5, the magnetic field is 0.15 G.
The lines of the

|
| Figure 2 |
[11] The vacuum medium cannot be described in the framework of the MHD approximation. For this reason, at t=0 in the computational domain, an extremely low concentration of 10-1 cm -3, whose influence on the dynamics of the corona plasma that expanded in the computational domain was negligibly small, was specified. At the initial moment of time, the temperature inside the region was taken to be as low as 20 eV.
[12] At
t = 0, a thermal expansion of the corona began. The corona
parameters ( rc/mi = 2 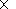 107 cm
-3,
Tc = 200 eV) were specified on the face
x=0 in the circle formed by the intersection of this face and a spherical
surface with the center ( -0.217, 0.5, 0.5) and radius
2R (Figure 1). The
center of the circle was ( y=0.5,
z=0.5 ), and its radius was 0.125. The
velocity of plasma outflow from the corona was found from the
continuity equation, so that the mass flow in the numerical experiment
corresponded to the loss of the Sun's mass carried away by the solar
wind (
107 cm
-3,
Tc = 200 eV) were specified on the face
x=0 in the circle formed by the intersection of this face and a spherical
surface with the center ( -0.217, 0.5, 0.5) and radius
2R (Figure 1). The
center of the circle was ( y=0.5,
z=0.5 ), and its radius was 0.125. The
velocity of plasma outflow from the corona was found from the
continuity equation, so that the mass flow in the numerical experiment
corresponded to the loss of the Sun's mass carried away by the solar
wind ( 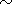 10-14 of the Sun's mass per year). From this condition, the
velocity of inflow into the region
Vx=2.5
10-14 of the Sun's mass per year). From this condition, the
velocity of inflow into the region
Vx=2.5 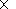 10-4 was specified at the
boundary
x=0 in the circle with the center ( y=0.5,
z=0.5 ) and radius
0.125. The self-consistent values of
r,
T, and
V automatically established
in the process of numerical solution of the MHD equations at thermal
expansion of corona plasma. The current of the current sheet could freely
flow in and out through the planes
y=0 and
y=1.
10-4 was specified at the
boundary
x=0 in the circle with the center ( y=0.5,
z=0.5 ) and radius
0.125. The self-consistent values of
r,
T, and
V automatically established
in the process of numerical solution of the MHD equations at thermal
expansion of corona plasma. The current of the current sheet could freely
flow in and out through the planes
y=0 and
y=1.
[13] It should be noted that, formally, the parameter
b0 did not correspond to
the ratio between pressures at any point. At the point
x=0,
y=0.5, and
z=0.5 the
b parameter is 8. In the vicinity of this point in the
computational domain, where the condition approximated the vacuum
one,
b=4 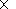 10-9 at the initial moment.
10-9 at the initial moment.
[14] The most delicate problem in specifying the boundary conditions is setting the magnetic field at the rightmost boundary X=1. In the process of calculations, and hence extension of field lines along the X axis, all components ( Bx, By, Bz ) undergo significant changes, and the tilt of the field line with respect to the X=1 plane also changes. Therefore it is impossible to specify the magnetic field at the boundary X=1. Setting j=0 is also unacceptable because, in the process of extension of field lines, the current sheet reaches the right boundary. The best approximation is to assume dj/dx=0. To be more certain that the obtained solution corresponds to the conditions in the solar wind, a layer boundary X=1 which is by a factor of 2-3 thicker than the current sheet can be excluded from the consideration.

Powered by TeXWeb (Win32, v.2.0).