2. Grassberger-Procaccia (GP) Algorithm

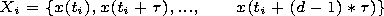
[3]  In the general case, the dynamics of a nonlinear dissipative system is described by a trajectory in phase space. Formally the system can have many degrees of freedom (parameters), however it can be shown that in many cases the behavior of the dynamic systems basically depends on a small number of critical parameters. In other words, the trajectory of a system in phase space lies near a low-dimensional surface of attraction. If we consider the one-dimensional set of measurements as a section (projection) of this trajectory, it is possible to estimate the dimension of this trajectory, designing multidimensional vectors by the data set [Grassberger and Procaccia, 1983]. This method is especially justified when it is impossible from other reasons to determine the number of independent variables for the system or to make their simultaneous measurement.

[4]  Usually, the calculation proceeds as follows [Grassberger and Procaccia, 1983]. From the experimental temporal set x(t), consisting of measured values, d -dimensional vectors X_n (n = 0, 1,..) are formed. The coordinates of these vectors consist of subsets of x(t) with consistently growing shifts, divisible into time of data quantization, i.e.,

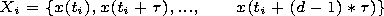(1)

At rather large shift the X_n vectors are independent; therefore they can be accepted as a sequence of points in d -dimensional embedding phase space. For the time of quantization the recommended choice is equal to 1/2 or 1/4 of time, at which the autocorrelation function of x(t) reaches a first minimum.

[5]  The correlation integral is calculated on the set of X_n. The correlation integral determines probability pays off that distance between a pair of vectors is less than the given distance r:

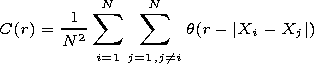(2)

where q is the Heaviside function and N is the number of vectors in the set. If the correlation integral depends on r through a power law C(r) 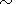r^b, then the degree parameter represents the correlation dimension of the process b=D_c. This dimension is a lower estimate of the Hausdorf dimension D, D_c 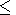D. Practically, for determination D_c it is necessary to construct the dependence lnC (r) on lnr at various growing dimensions of embedding space. The calculation finishes once the inclination of the diagram no longer varies as d increases. The estimated value of D_c is considered rather reliable, if it does not vary up to d=2Dc + 1.

[6]  The method described here is usually applied to estimate the correlation dimension at D_c < 10, and it is used as evidence for the benefit of that the behavior of system is described by small number of differential equations. If the received value of D_c is not an integer, then it is said that the system has a fractal (strange) attractor. In case of white noise at any value of d saturation of the correlation integral does not occur and C(r) 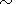r^d. If in the experimental data set, there is noise with amplitude r_o, then for scales r<2r_o the behavior of the correlation integral corresponds to the expression for white noise. However, for scales r>2r_o the presence of noise does not influence the behavior of the correlation integral. This property allows us to separate a chaotic process of dynamic origin from additive white noise.

[7]  The calculation of correlation dimension on various geophysical data was carried out in many papers. A number of papers were devoted to the analysis of the fractal dimension of AE and AL indexes [see Kiselev and Kryvoi, 1996, and references therein]. Ovezgel'dyev et al. [1992] show the presence of a low-dimensional strange attractor in variations of the E_s layer. Bespalov and Sidorovskaya [1992] investigated the dimension of LF chorus. Wang [1996] suggested using the correlation dimension, determined from measurements of magnetic field at low latitudes, as a characteristic of solar activity.

[8]  A correct choice of quantization step ( t ) and general number of points in the data set ( N ) are the most essential parameters, which influenced results of the calculation of correlation dimension by the Grassberger-Procaccia method. Atmanspacher et al. [1988], Bingham and Kot [1989], Ellner [1988], Roberts [1991], Shi-Zhong and Shi-Ming [1994], Smith [1988], Takens [1993], and Theiler [1988] discussed different applications of this method, its restrictions, but also extensions. Theiler gave the most optimistic estimate of the minimum number of points in the data set necessary for obtaining the correlation dimension: N>2^1/2[(27.5)^1/2]^D, where D is the correlation dimension.